变化率的测量是微分学中不可或缺的概念,微分学涉及变化和无穷小的数学。它使我们能够找到两个变化变量之间的关系以及它们如何相互影响。
变化率的测量对于机器学习也至关重要,例如在应用梯度下降作为优化算法来训练神经网络模型时。
在本教程中,您将发现变化率作为微积分中的一个关键概念,以及测量它的重要性。
完成本教程后,您将了解:
- 如何测量线性和非线性函数的变化率。
- 为什么变化率的测量在不同领域是一个重要的概念。
让我们开始吧。

微积分的关键概念:变化率
图片由Spencer Everett提供,保留部分权利。
教程概述
本教程分为两部分;它们是
- 变化率
- 测量变化率的重要性
变化率
变化率定义了一个变化变量相对于另一个变化变量的关系。
考虑一个移动的物体,它在垂直方向(用y表示)上的位移是水平方向(用x表示)上的两倍。用数学术语表示,这可以表示为
????y = 2????x
希腊字母delta,????,通常用于表示差值或变化。因此,上述方程定义了移动物体x位置变化与y位置变化之间的关系。
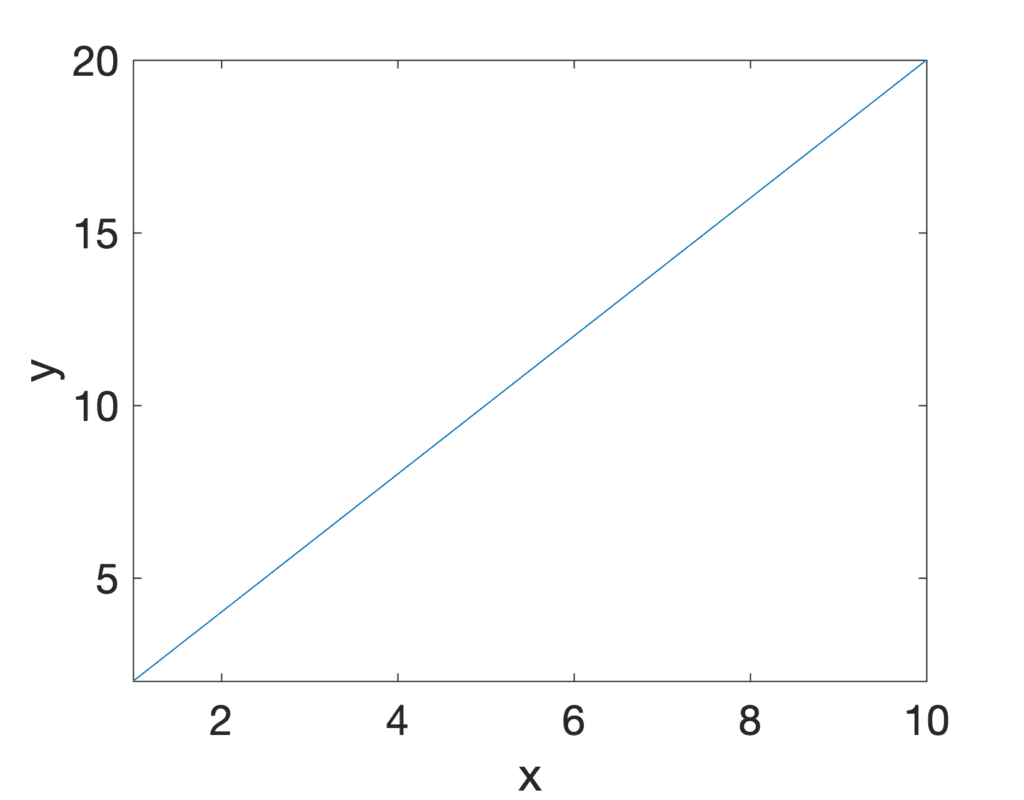
x和y方向上的这种变化可以通过x–y坐标系上的直线来绘制。
在这个物体运动的图形表示中,变化率由直线的斜率或其梯度表示。由于直线每向右“运行”一个单位就“上升”2个单位,因此其变化率或斜率等于2。
速率和斜率之间有一个简单的联系。先前的速率示例可以在x-y坐标系上绘制,其中每个速率都显示为一个斜率。
第38页,微积分要点傻瓜书,2019年。
把所有东西联系起来,我们看到
变化率 = ????y / ????x = 上升 / 水平移动 = 斜率
如果我们要考虑这条直线上两个特定点P1 = (2, 4)和P2 = (8, 16),我们可以确认斜率等于
斜率 = ????y / ????x = (y2 – y1) / (x2 – x1) = (16 – 4) / (8 – 2) = 2
对于这个特定示例,由斜率表示的变化率是正的,因为直线的方向向右增加。但是,如果直线的方向减小,变化率也可以是负的,这意味着随着x值的增加,y值会减小。此外,当x增加而y值保持不变时,我们会说变化率为零。反之,如果y增加而x值保持不变,我们会认为变化范围是无限的,因为垂直线的斜率被认为是未定义的。
到目前为止,我们考虑了最简单的直线示例,因此是具有不变斜率的线性函数。然而,并非所有函数都如此简单,如果它们是,也就不需要微积分了。
微积分是关于变化的数学,所以现在是时候转向抛物线了,那些斜率变化的曲线。
第39页,微积分要点傻瓜书,2019年。
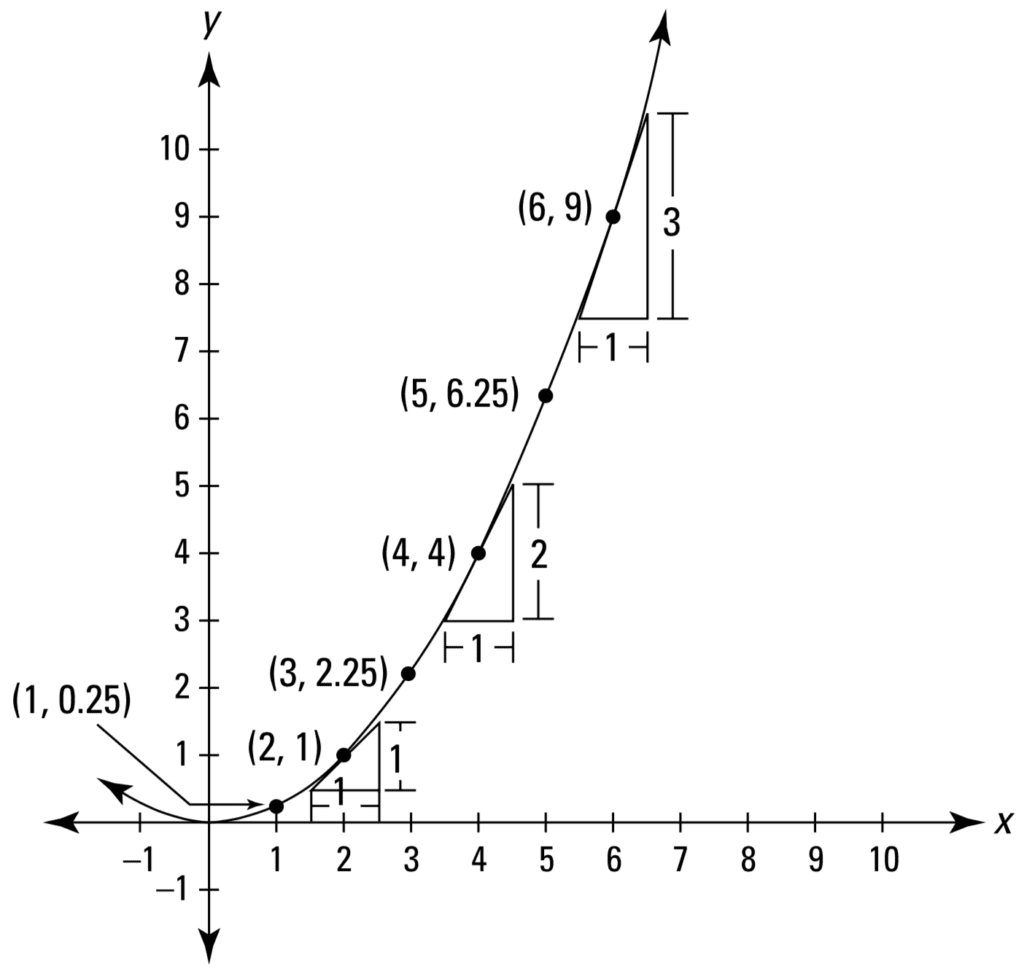
让我们考虑一个简单的非线性函数,一个抛物线
y = (1 / 4) x2
与特征直线的恒定斜率不同,我们可能会注意到这个抛物线在向右移动时变得越来越陡峭。
回想一下,微积分的方法允许我们通过将弯曲形状切割成许多并排排列的无穷小直线段来分析它。如果我们要考虑其中一个在抛物线弯曲形状上某个特定点P的段,我们会发现我们再次将变化率计算为直线的斜率。重要的是要记住,抛物线上的变化率取决于我们最初考虑的特定点P。
例如,如果我们要考虑通过点P = (2, 1)的直线,我们发现在抛物线上该点的变化率为
变化率 = ????y / ????x = 1 / 1 = 1
如果我们要考虑同一抛物线上不同点P = (6, 9),我们发现在该点的变化率等于
变化率 = ????y / ????x = 3 / 1 = 3
在某个特定点P触碰曲线的直线被称为切线,而计算函数变化率的过程也称为求其导数。
导数只是衡量一件事相对于另一件事变化多少的量度——这就是一个速率。
第37页,微积分要点傻瓜书,2019年。
虽然我们在此示例中考虑了一个简单的抛物线,但我们同样可以使用微积分来分析更复杂的非线性函数。计算曲线上不同切点处的瞬时变化率的概念保持不变。
当我们使用梯度下降算法训练神经网络时,我们会遇到这样一个例子。作为优化算法,梯度下降通过迭代方式使误差函数趋向其全局最小值,每次更新神经网络权重以更好地模拟训练数据。误差函数通常是非线性的,并且可能包含许多局部最小值和鞍点。为了找到下坡的路,梯度下降算法计算误差函数上不同点处的瞬时斜率,直到达到误差最低且变化率为零的点。
测量变化率的重要性
到目前为止,我们已经考虑了x–y坐标系上每单位的变化率。
但一个速率可以是任何东西的任何东西。
第38页,微积分要点傻瓜书,2019年。
例如,在训练神经网络的背景下,我们已经看到误差梯度被计算为误差相对于神经网络中特定权重的变化。
在许多不同的领域中,变化率的测量也是一个重要的概念。一些例子是
- 在物理学中,速度被计算为单位时间内位置的变化。
- 在信号数字化中,采样率被计算为每秒的信号样本数。
- 在计算中,比特率是计算机每单位时间处理的比特数。
- 在金融中,汇率指一种货币相对于另一种货币的价值。
无论哪种情况,每个速率都是导数,每个导数都是速率。
第38页,微积分要点傻瓜书,2019年。
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
书籍
总结
在本教程中,您了解了变化率作为微积分中的一个关键概念,以及测量它的重要性。
具体来说,你学到了:
- 变化率的测量是微分学中不可或缺的概念,它使我们能够找到一个变化变量相对于另一个变化变量的关系。
- 这是一个可以应用于许多领域的重要概念,其中之一就是机器学习。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。






“在物理学中,速度被计算为单位时间内位置的变化。”
我的Garmin手表实时显示我当前的跑步配速,例如6分钟/公里!
我想,这也是“每个速率都是导数”——它是否在手表中即时计算?