线搜索是一种可用于具有一个或多个变量的目标函数的优化算法。
它提供了一种方法,通过在每个维度上使用搜索来定位从已知点到最优点的最佳步长,从而将一元优化算法(如二分查找)应用于多元目标函数。
在本教程中,您将学习如何在 Python 中执行线搜索优化。
完成本教程后,您将了解:
- 线性搜索是用于一元和多元优化问题的优化算法。
- SciPy 库提供了用于执行线搜索的 API,该搜索要求您知道如何计算目标函数的一阶导数。
- 如何对目标函数执行线搜索并使用结果。
通过我的新书 《机器学习优化》 快速启动您的项目,其中包含分步教程和所有示例的Python 源代码文件。
让我们开始吧。
使用 Python 进行线搜索优化
照片来自 Nathalie,部分权利保留。
教程概述
本教程分为三个部分;它们是:
- 什么是线搜索
- Python 中的线搜索
- 如何执行线搜索
- 定义目标函数
- 执行线搜索
- 处理线搜索失败的情况
什么是线搜索
线搜索是用于一元或多元优化的优化算法。
该算法需要搜索空间中的初始位置和要搜索的方向。然后,它将从初始位置在搜索空间中选择下一个位置,该位置将产生更好的或最佳的目标函数评估。
方向是指示沿直线的符号(正或负)和搜索的最大范围的幅度。因此,方向最好被视为候选搜索区域,并且必须足够大以包含最优值或优于起始点的点。
线搜索将自动选择一个称为 alpha 的比例因子作为步长(方向),从当前位置开始,以最小化目标函数。这涉及使用另一个一元优化算法来找到所选方向上的最佳点,以选择合适的 alpha。
一种方法是使用线搜索,该方法选择最小化一维函数的步长因子 [...] 我们可以应用我们选择的一元优化方法。
— 第 54 页,《优化算法》,2019 年。
Alpha 是方向的比例因子,因此在搜索中仅考虑 0.0 到 1.0 之间的值。线搜索的单步解决了最小化问题,该问题最小化当前位置加上缩放方向的目标函数
- 最小化 objective(position + alpha * direction)
因此,线搜索一次只在一个维度上运行,并返回沿选定方向移动的距离。
线搜索方法的每次迭代都会计算一个搜索方向 pk,然后决定沿该方向移动多远。
— 第 30 页,《数值优化》,2006 年。
线搜索可以反复调用以导航搜索空间到解决方案,并且如果选择的方向不包含具有更低目标函数值的点(例如,如果算法被指示向上搜索)则可能失败。
解决方案是近似的或不精确的,并且可能不是全局解决方案,具体取决于搜索空间的形状。此算法适用的条件称为沃尔夫条件。
现在我们熟悉了线搜索,让我们探讨一下如何在 Python 中执行线搜索。
想要开始学习优化算法吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
Python 中的线搜索
我们可以使用 line_search() 函数手动在 Python 中执行线搜索。
它支持一元优化以及多元优化问题。
此函数接受目标函数的名称和目标函数的梯度名称,以及搜索空间中的当前位置和移动方向。
因此,您必须了解目标函数的一阶导数。您还必须对从哪里开始搜索以及搜索的范围有所了解。回想一下,您可以多次使用不同的方向(符号和幅度)进行搜索。
|
1 2 |
... result = line_search(objective, gradient, point, direction) |
该函数返回一个包含六个元素的元组,其中包括称为 alpha 的方向比例因子以及执行的函数评估次数等。
结果元组中的第一个元素包含 alpha。如果搜索未收敛,alpha 的值将为 None。
|
1 2 3 |
... # 检索作为线搜索一部分找到的 alpha 值 alpha = result[0] |
alpha、起始点和方向可用于构建单次线搜索的终点。
|
1 2 3 |
... # 构建线搜索的终点 end = point + alpha * direction |
对于具有多个输入变量(例如多元优化)的优化问题,line_search() 函数将为所有维度返回单个 alpha 值。
这意味着该函数假定最优值在所有维度上与起始点等距,这是一个重大限制。
现在我们熟悉了如何在 Python 中执行线搜索,让我们来探讨一个实际示例。
如何执行线搜索
我们可以使用一个简单的一元目标函数及其导数来演示如何使用线搜索。
本节分为多个部分,包括定义测试函数、执行线搜索以及处理未找到最优值的失败情况。
定义目标函数
首先,我们可以定义目标函数。
在这种情况下,我们将使用一个一维目标函数,特别是偏离零值的一个小量。这是一个凸函数,选择它的原因是它易于理解和计算其一阶导数。
- objective(x) = (-5 + x)^2
请注意,线搜索不仅限于一维函数或凸函数。
此函数的实现如下所示。
|
1 2 3 |
# 目标函数 def objective(x): return (-5.0 + x)**2.0 |
此函数的一阶导数可以解析计算,如下所示
- gradient(x) = 2 * (-5 + x)
每个输入值的梯度仅表示每个点的导向最优值的斜率。此函数的实现如下所示。
|
1 2 3 |
# 目标函数的梯度 def gradient(x): return 2.0 * (-5.0 + x) |
我们可以将 x 的输入范围定义为 -10 到 20,并计算每个输入的客观值。
|
1 2 3 4 5 6 7 |
... # 定义范围 r_min, r_max = -10.0, 20.0 # 准备输入 inputs = arange(r_min, r_max, 0.1) # 计算目标值 targets = [objective(x) for x in inputs] |
然后,我们可以绘制输入值与目标值,以了解函数的形状。
|
1 2 3 4 5 |
... # 绘制输入与目标的图 pyplot.plot(inputs, targets, '-', label='objective') pyplot.legend() pyplot.show() |
将这些结合起来,完整的示例列在下面。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
# 绘制凸目标函数 from numpy import arange from matplotlib import pyplot # 目标函数 def objective(x): return (-5.0 + x)**2.0 # 目标函数的梯度 def gradient(x): return 2.0 * (-5.0 + x) # 定义范围 r_min, r_max = -10.0, 20.0 # 准备输入 inputs = arange(r_min, r_max, 0.1) # 计算目标值 targets = [objective(x) for x in inputs] # 绘制输入与目标的图 pyplot.plot(inputs, targets, '-', label='objective') pyplot.legend() pyplot.show() |
运行示例,评估范围从 -10 到 20 的输入值(x),并创建显示熟悉的抛物线 U 形的图。
函数的最优值似乎在 x=5.0,目标值为 0.0。
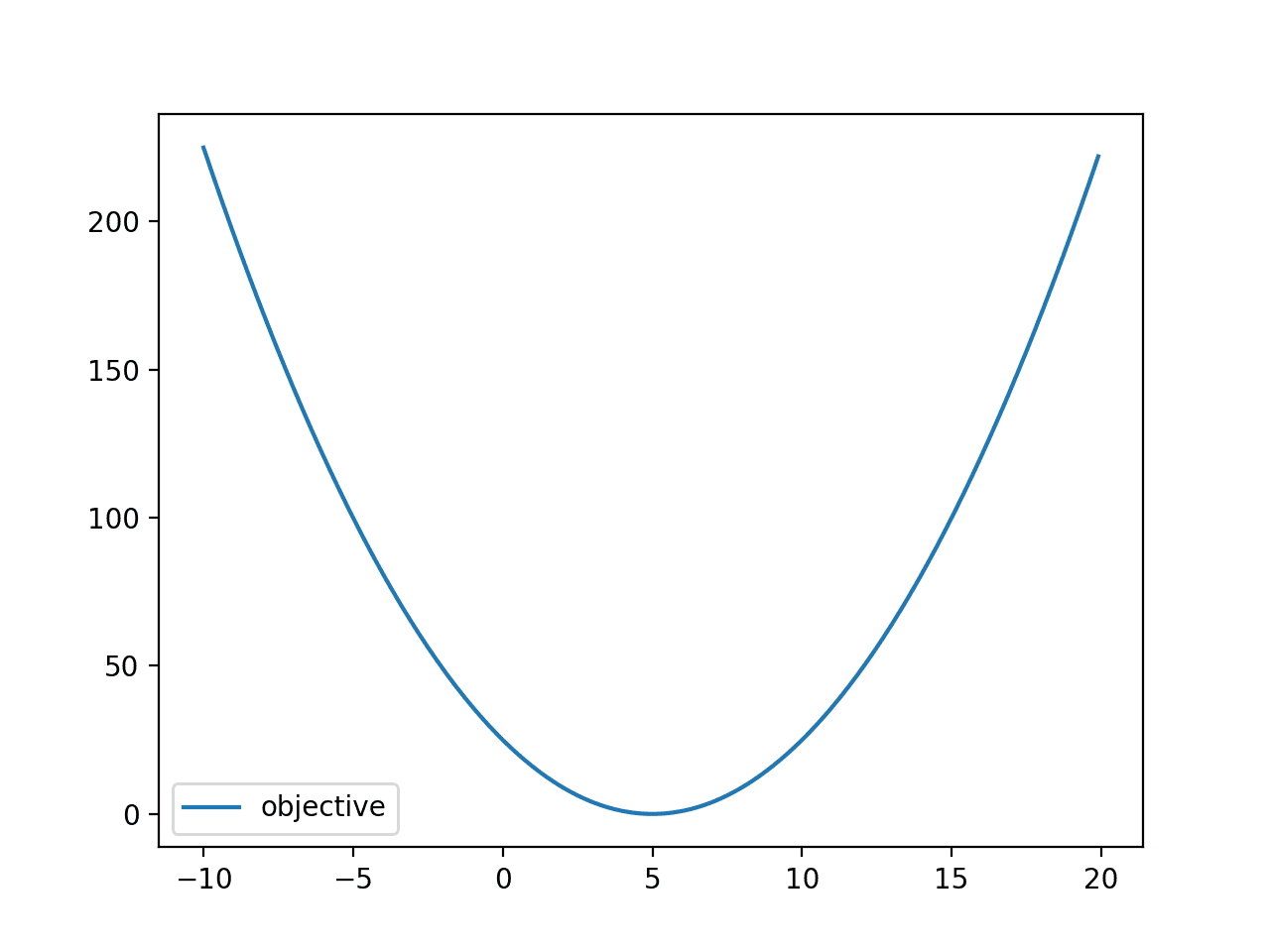
凸目标函数的线图
执行线搜索
接下来,我们可以对函数执行线搜索。
首先,我们必须定义搜索的起始点和搜索方向。
在这种情况下,我们将使用起始点 x=-5,这距离最优值大约 10 个单位。我们将向右迈出一大步,例如正方向,在本例中为 100 个单位,这将大大超出最优值。
回想一下,方向就像步长,搜索将缩放步长以找到最优值。
|
1 2 3 4 5 6 7 8 9 |
... # 定义起始点 point = -5.0 # 定义移动方向 direction = 100.0 # 打印初始条件 print('start=%.1f, direction=%.1f' % (point, direction)) # 执行线搜索 result = line_search(objective, gradient, point, direction) |
然后,搜索将寻找最优值并返回修改方向以找到最优值的 alpha 或距离。
我们可以从结果中获取 alpha,以及执行的函数评估次数。
|
1 2 3 4 5 |
... # 总结结果 alpha = result[0] print('Alpha: %.3f' % alpha) print('Function evaluations: %d' % result[1]) |
我们可以使用 alpha、起始点和步长来计算最优值的位置,并计算该点的目标函数(我们期望它等于 0.0)。
|
1 2 3 4 5 |
... # 定义目标函数最小值 end = point + alpha * direction # 评估目标函数最小值 print('f(end) = %.3f' % objective(end)) |
然后,为了好玩,我们可以再次绘制函数并显示起始点(绿色方块)和终点(红色方块)。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
... # 定义范围 r_min, r_max = -10.0, 20.0 # 准备输入 inputs = arange(r_min, r_max, 0.1) # 计算目标值 targets = [objective(x) for x in inputs] # 绘制输入与目标的图 pyplot.plot(inputs, targets, '--', label='objective') # 绘制搜索的起点和终点 pyplot.plot([point], [objective(point)], 's', color='g') pyplot.plot([end], [objective(end)], 's', color='r') pyplot.legend() pyplot.show() |
将以上内容整合起来,执行凸目标函数线搜索的完整示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
# 对凸目标函数执行线搜索 from numpy import arange from scipy.optimize import line_search from matplotlib import pyplot # 目标函数 def objective(x): return (-5.0 + x)**2.0 # 目标函数的梯度 def gradient(x): return 2.0 * (-5.0 + x) # 定义起始点 point = -5.0 # 定义移动方向 direction = 100.0 # 打印初始条件 print('start=%.1f, direction=%.1f' % (point, direction)) # 执行线搜索 result = line_search(objective, gradient, point, direction) # 总结结果 alpha = result[0] print('Alpha: %.3f' % alpha) print('Function evaluations: %d' % result[1]) # 定义目标函数最小值 end = point + alpha * direction # 评估目标函数最小值 print('f(end) = f(%.3f) = %.3f' % (end, objective(end))) # 定义范围 r_min, r_max = -10.0, 20.0 # 准备输入 inputs = arange(r_min, r_max, 0.1) # 计算目标值 targets = [objective(x) for x in inputs] # 绘制输入与目标的图 pyplot.plot(inputs, targets, '--', label='objective') # 绘制搜索的起点和终点 pyplot.plot([point], [objective(point)], 's', color='g') pyplot.plot([end], [objective(end)], 's', color='r') pyplot.legend() pyplot.show() |
运行示例,首先报告起始点和方向。
执行搜索并找到一个 alpha 值,该值修改方向以找到最优值,在本例中为 0.1,在三次函数评估后找到。
最优值点位于 5.0,评估结果为 0.0,符合预期。
|
1 2 3 4 |
start=-5.0, direction=100.0 Alpha: 0.100 Function evaluations: 3 f(end) = f(5.000) = 0.000 |
最后,创建函数图,显示起始点(绿色)和目标(红色)。
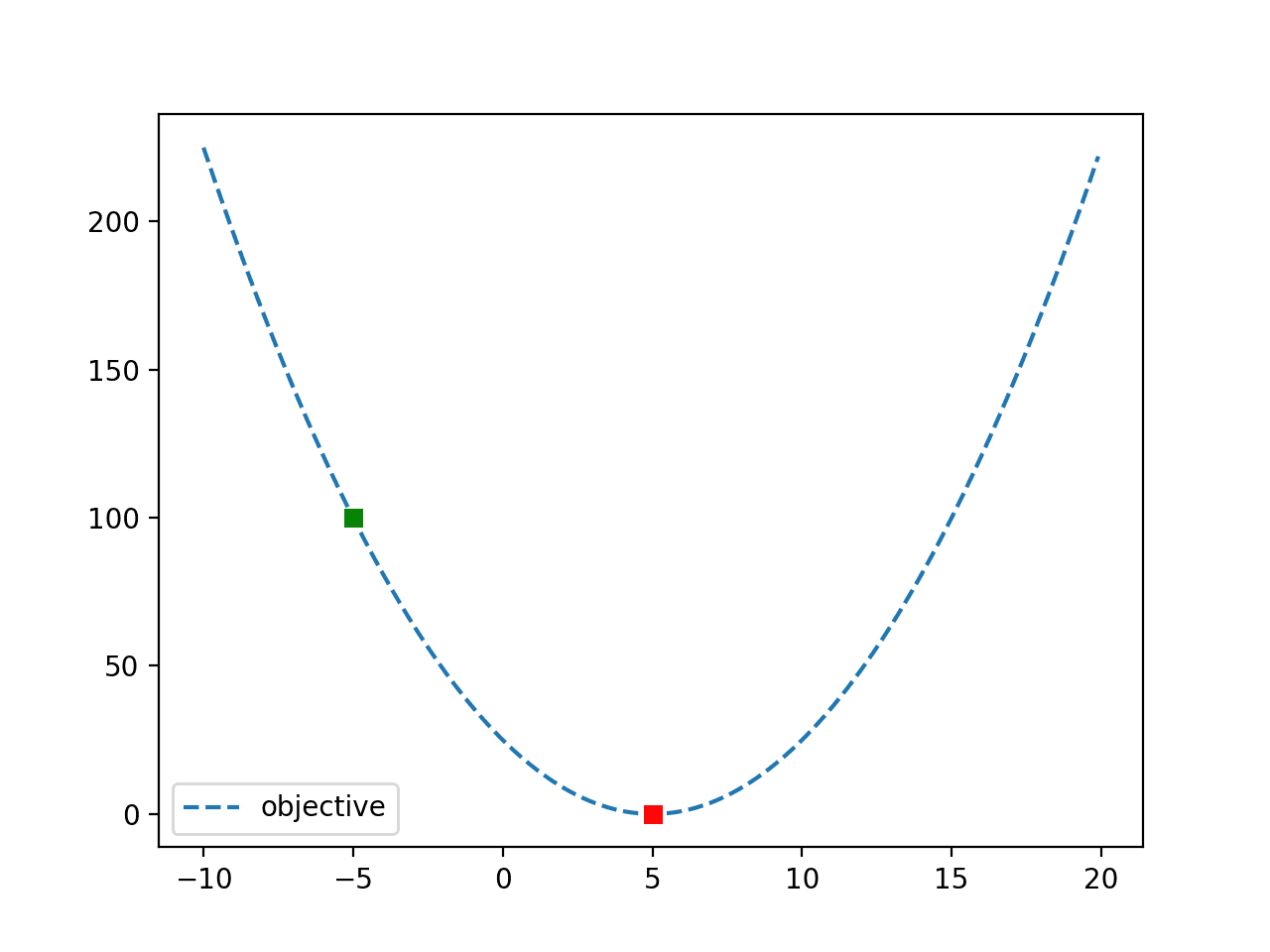
带有搜索起始点和最优值的目标函数线图
处理线搜索失败的情况
搜索不能保证找到函数的全局最优值。
如果指定的方向不足以包含最优值,则可能发生这种情况。
例如,如果我们使用方向值为 3,那么搜索将无法找到最优值。我们可以通过一个完整的示例来演示这一点,如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
# 对具有过小方向的凸目标函数执行线搜索 from numpy import arange from scipy.optimize import line_search from matplotlib import pyplot # 目标函数 def objective(x): return (-5.0 + x)**2.0 # 目标函数的梯度 def gradient(x): return 2.0 * (-5.0 + x) # 定义起始点 point = -5.0 # 定义移动方向 direction = 3.0 # 打印初始条件 print('start=%.1f, direction=%.1f' % (point, direction)) # 执行线搜索 result = line_search(objective, gradient, point, direction) # 总结结果 alpha = result[0] print('Alpha: %.3f' % alpha) # 定义目标函数最小值 end = point + alpha * direction # 评估目标函数最小值 print('f(end) = f(%.3f) = %.3f' % (end, objective(end))) |
运行示例,搜索达到 alpha 限制 1.0,导致终点为 -2,评估值为 49。距离最优值 f(5) = 0.0 还有很长的路要走。
|
1 2 3 |
start=-5.0, direction=3.0 Alpha: 1.000 f(end) = f(-2.000) = 49.000 |
此外,我们可以选择一个只导致比起始点更差的评估的错误方向。
在这种情况下,错误的方向将是远离最优值的负方向,例如,从起始点向上所有方向。
|
1 2 3 4 5 |
... # 定义起始点 point = -5.0 # 定义移动方向 direction = -3.0 |
预期是搜索不会收敛,因为它无法找到比起始点更好的点。
搜索不收敛的完整示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
# 对不收敛的凸目标函数执行线搜索 from numpy import arange from scipy.optimize import line_search from matplotlib import pyplot # 目标函数 def objective(x): return (-5.0 + x)**2.0 # 目标函数的梯度 def gradient(x): return 2.0 * (-5.0 + x) # 定义起始点 point = -5.0 # 定义移动方向 direction = -3.0 # 打印初始条件 print('start=%.1f, direction=%.1f' % (point, direction)) # 执行线搜索 result = line_search(objective, gradient, point, direction) # 总结结果 print('Alpha: %s' % result[0]) |
运行示例,结果是 LineSearchWarning,表明搜索未能收敛,符合预期。
从搜索返回的 alpha 值为 None。
|
1 2 3 4 |
start=-5.0, direction=-3.0 LineSearchWarning: 线搜索算法未收敛 warn('The line search algorithm did not converge', LineSearchWarning) Alpha: None |
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
书籍
API
文章
总结
在本教程中,您学习了如何在 Python 中执行线搜索优化。
具体来说,你学到了:
- 线性搜索是用于一元和多元优化问题的优化算法。
- SciPy 库提供了用于执行线搜索的 API,该搜索要求您知道如何计算目标函数的一阶导数。
- 如何对目标函数执行线搜索并使用结果。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。






你好 Jason。很棒的教程!
我想知道是否有一种方法也可以找到最佳方向。也许这取决于方法?例如,在梯度下降中,我们使用梯度在当前点作为方向。对吗?
另外,为什么在梯度下降用于训练机器学习模型时,不使用这种方法来查找 alpha 参数?
致以最诚挚的问候。
导数(如果我们能计算它的话)指向正确的方向(或者说是梯度的负方向)。
这种方法最适合凸问题,也许是一维问题。
你好 Jason – 这非常好。您是在展示精确线搜索还是非精确线搜索算法的实现?
你好 Prakash…实现基于以下内容:
https://docs.scipy.org.cn/doc/scipy/reference/generated/scipy.optimize.line_search.html