注意力操作是 Transformer 模型的标志,但它们并非唯一的构建块。线性层和激活函数同样至关重要。在这篇文章中,您将了解到:
- 为什么线性层和激活函数能够实现非线性变换
- Transformer 模型中前馈网络的典型设计
- 常见的激活函数及其特点
让我们开始吧。

Transformer 模型中的线性层和激活函数
图片来源:Svetlana Gumerova。保留部分权利。
概述
这篇博文分为三部分;它们是:
- Transformer 中为何需要线性层和激活函数
- 前馈网络的典型设计
- 激活函数的变体
Transformer 中为何需要线性层和激活函数
注意力层是 Transformer 模型的核心功能。它对序列中的不同元素进行对齐,并将输入序列转换为输出序列。注意力层对输入执行仿射变换,这意味着输出是每个序列元素输入的加权和。
神经网络之所以强大,不仅在于线性层,更在于引入非线性的激活函数。在 Transformer 模型中,注意力层之后需要非线性来学习复杂的模式。这通过在每个注意力层之后添加一个前馈网络(FFN)或多层感知机(MLP)来实现。一个典型的 Transformer 块如下所示:
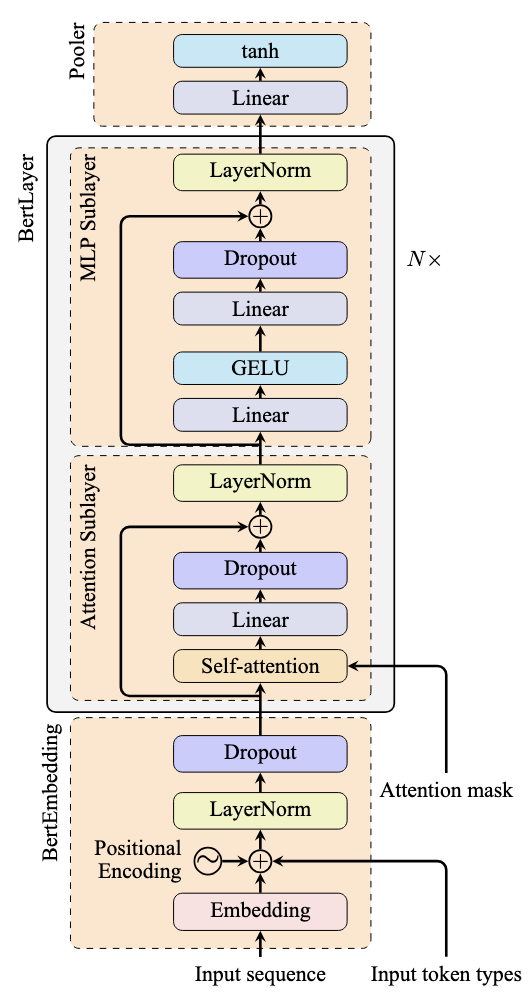
BERT 模型架构
上图中灰色方框在 Transformer 模型中会重复多次。在每个块中(不包括归一化层),输入首先通过注意力层,然后通过前馈网络(在 PyTorch 中实现为 nn.Linear)。前馈网络中的激活函数为变换增加了非线性。
前馈网络允许模型学习更复杂的模式。通常,它包含多个线性层:第一个层扩展维度以探索不同的表示,而最后一个层将其收缩回原始维度。激活函数通常应用于第一个线性层的输出。
由于这种设计,我们通常将块的前半部分称为“注意力子层”,后半部分称为“MLP 子层”。
前馈网络的典型设计
在 BERT 模型中,MLP 子层的实现如下:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
import torch.nn as nn class BertMLP(nn.Module): def __init__(self, dim, intermediate_dim): super().__init__() self.fc1 = nn.Linear(dim, intermediate_dim) self.fc2 = nn.Linear(intermediate_dim, dim) self.gelu = nn.GELU() def forward(self, hidden_states): hidden_states = self.fc1(hidden_states) hidden_states = self.gelu(hidden_states) hidden_states = self.fc2(hidden_states) return hidden_states |
MLP 子层包含两个线性模块。当输入序列进入 MLP 子层时,第一个线性模块扩展维度,然后应用 GELU 激活函数。结果通过第二个线性模块收缩维度回原始大小。
中间维度通常是原始维度的 4 倍:这是 Transformer 模型中常见的设计模式。
激活函数的变体
激活函数将非线性引入神经网络,使其能够学习复杂的模式。虽然传统神经网络通常使用双曲正切 (tanh)、Sigmoid 和修正线性单元 (ReLU),但 Transformer 模型通常采用 GELU 和 SwiGLU 激活函数。
以下是一些常见激活函数的数学定义:
$$
\begin{aligned}
$\text{Sigmoid}(x) &= \frac{1}{1 + e^{-x}} \\$
$\tanh(x) &= \frac{e^x – e^{-x}}{e^x + e^{-x}} = 2\text{Sigmoid}(2x) – 1 \\$
$\text{ReLU}(x) &= \max(0, x) \\$
$\text{GELU}(x) &= x \cdot \Phi(x) \approx \frac{x}{2}\Big(1 + \tanh\big(\sqrt{\frac{2}{\pi}}(x + 0.044715x^3)\big)\Big) \\$
$\text{Swish}_\beta(x) &= x \cdot \text{Sigmoid}(\beta x) = \frac{x}{1 + e^{-\beta x}} \\$
$\text{SiLU}(x) &= \frac{x}{1 + e^{-x}} = \text{Swish}_1(x) \\$
$\text{SwiGLU}(x) &= \text{SiLU}(xW + b) \cdot (xV + c)$
\end{aligned}
$$
ReLU(修正线性单元)在现代深度学习中很受欢迎,因为它避免了梯度消失问题并且计算简单。
GELU(高斯误差线性单元)由于使用了标准正态分布的累积分布函数 $\Phi(x)$,因此计算成本更高。如上所示,存在一个近似公式。GELU 不是单调的,如下图所示。
通常首选单调激活函数,因为它们能确保一致的梯度方向,可能导致更快的收敛。然而,单调性并非严格要求——您可能只需要更长的训练时间。您权衡的是模型复杂性和训练时长。
Swish 是另一个非单调激活函数,其参数 $\beta$ 控制 $x=0$ 处的斜率。当 $\beta=1$ 时,它被称为 SiLU(Sigmoid 线性单元)。
SwiGLU(Swish 门控线性单元)是现代 Transformer 模型中常见的一种最新激活函数。它是 Swish 函数和线性函数的乘积,其参数在训练过程中学习。它之所以受欢迎,源于其复杂性:展开公式会发现分子中包含一个二次项,这有助于模型在不增加额外层的情况下学习复杂的模式。
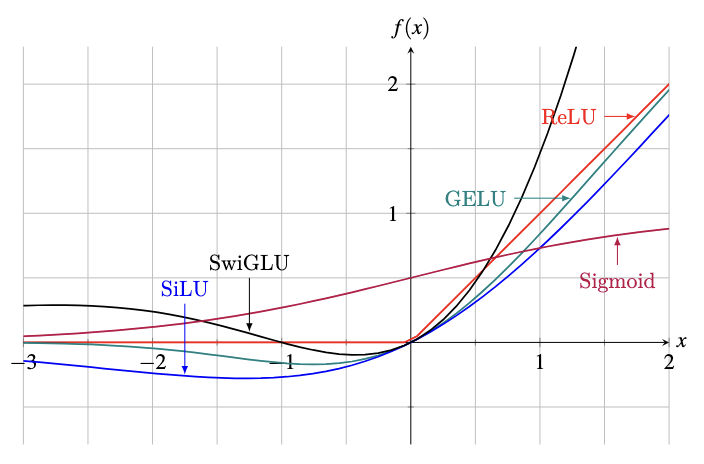
一些常见激活函数的曲线图
上图显示了这些激活函数的曲线图。所示的 SwiGLU 函数为 $f(x) = \text{SiLU}(x) \cdot (x+1)$。
在 Python 代码中切换激活函数很简单。PyTorch 提供了内置的 nn.Sigmoid、nn.ReLU、nn.Tanh 和 nn.SiLU。但是,SwiGLU 需要特殊实现。以下是 Llama 模型中使用的 PyTorch 代码:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
import torch.nn as nn class LlamaMLP(nn.Module): def __init__(self, dim, intermediate_dim): super().__init__() self.gate_proj = nn.Linear(dim, intermediate_dim) self.up_proj = nn.Linear(dim, intermediate_dim) self.down_proj = nn.Linear(intermediate_dim, dim) self.act = nn.SiLU() def forward(self, hidden_states): gate = self.gate_proj(hidden_states) up = self.up_proj(hidden_states) swish = self.act(up) output = self.down_proj(swish * gate) return hidden_states |
此实现使用两个线性层来处理输入 hidden_states。其中一个输出通过 SiLU 函数,然后与另一个输出相乘,最后通过一个线性层进行处理。线性层根据维度扩展/收缩而命名为“up”或“down”,而连接到 SiLU 的层因其门控机制而被称为“gate”。门控是一种神经网络设计,意味着一个线性层的输出与一个权重进行元素级乘法,这个权重由 Swish 激活函数生成。
Llama 模型架构如下所示,展示了 MLP 模块的双分支结构:
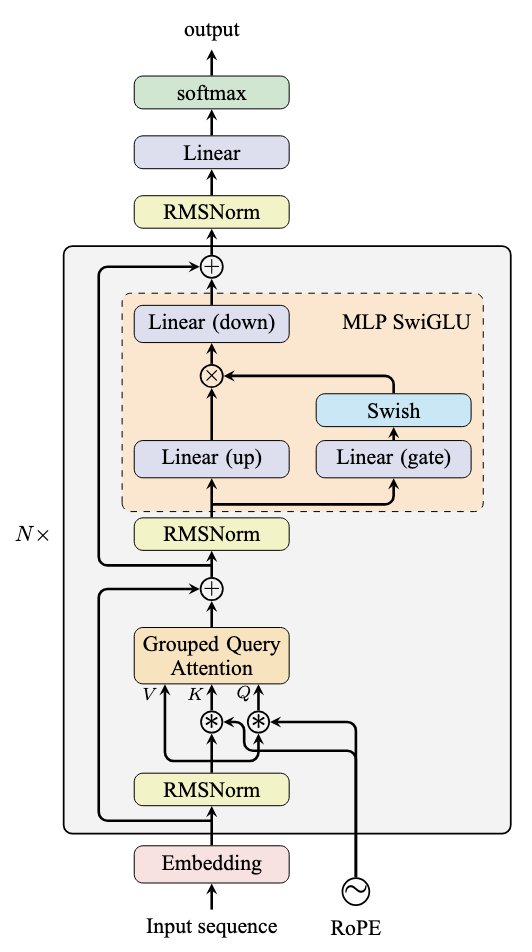
Llama 模型架构
进一步阅读
以下是一些您可能会觉得有用的资源:
- 注意力就是你所需要的一切
- 高斯误差线性单元 (GELUs)
- Swish:一种自门控激活函数
- GLU 变体改进 Transformer
- LLaMA:开放高效的基础语言模型
- PyTorch 线性 API 文档
- PyTorch 激活函数
- 为什么激活函数必须是单调的?
总结
在这篇文章中,您了解了 Transformer 模型中的线性层和激活函数。具体来说,您学习了:
- 为什么线性层和激活函数对于非线性变换是必需的
- ReLU、GELU 和 SwiGLU 激活函数的特点和实现
- 如何构建 Transformer 模型中使用的完整前馈网络






暂无评论。