线性回归可能是统计学和机器学习中最知名且最易理解的算法之一。
在这篇文章中,你将了解线性回归算法、它的工作原理以及如何在机器学习项目中最好地使用它。在这篇文章中你将学到:
- 为什么线性回归同时属于统计学和机器学习。
- 线性回归的诸多名称。
- 用于创建线性回归模型的表示和学习算法。
- 在使用线性回归进行建模时,如何最好地准备数据。
你不需要任何统计学或线性代数知识即可理解线性回归。这是一个对该技术的高层次简要介绍,旨在为你提供足够的背景知识,以便你能够有效地解决自己的问题。
2023年12月更新:
- 部分章节为清晰和解释而编辑。
- 新增从头开始构建线性回归模型部分。
通过我的新书《掌握机器学习算法》启动你的项目,包括分步教程和所有示例的Excel电子表格文件。
让我们开始吧。

机器学习中的线性回归
图片来源:Nicolas Raymond,保留部分权利。
线性回归不是统计学中的吗?
在我们深入了解线性回归的细节之前,你可能会问自己为什么我们要研究这个算法。
它不是统计学中的一种技术吗?
机器学习,更具体地说是预测建模领域,主要关注于最小化模型误差或尽可能做出最准确的预测,而牺牲可解释性。在应用机器学习中,我们将借鉴、重用和“窃取”来自许多不同领域的算法,包括统计学,并将其用于这些目的。
因此,线性回归是在统计学领域开发的,并作为理解输入和输出数值变量之间关系的模型进行研究,但已被机器学习借鉴。它既是一种统计算法,也是一种机器学习算法。
接下来,我们回顾一些常用来指代线性回归模型的名称。
获取您的免费算法思维导图
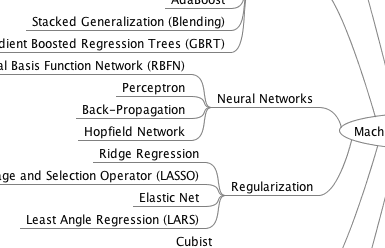
方便的机器学习算法思维导图样本。
我创建了一份方便的思维导图,其中包含60多种按类型组织的算法。
下载、打印并使用它。
还可以独家访问机器学习算法电子邮件迷你课程。
线性回归的众多名称
当你开始研究线性回归时,事情可能会变得非常混乱。
原因是线性回归已经存在了很长时间(200多年)。它已经从各个可能的角度进行了研究,而且通常每个角度都有一个新的、不同的名称。
线性回归是一个线性模型,即假设输入变量 (x) 和单个输出变量 (y) 之间存在线性关系的模型。更具体地说,y 可以通过输入变量 (x) 的线性组合来计算。
当只有一个输入变量 (x) 时,该方法被称为简单线性回归。当有多个输入变量时,统计学文献通常将该方法称为多元线性回归。
可以使用不同的技术从数据中准备或训练线性回归方程,其中最常见的一种称为普通最小二乘法。因此,通常将通过这种方式准备的模型称为普通最小二乘线性回归或仅称为最小二乘回归。
现在我们知道了描述线性回归的一些名称,让我们仔细看看所使用的表示。
线性回归模型表示
线性回归是一个吸引人的模型,因为它的表示非常简单。
表示是一个线性方程,它结合了一组特定的输入值 (x),其解是该组输入值 (y) 的预测输出。因此,输入值 (x) 和输出值都是数值。
线性方程为每个输入值或列分配一个比例因子,称为系数,用大写希腊字母 Beta (B) 表示。此外,还添加了一个额外的系数,使直线具有额外的自由度(例如,在二维图中上下移动),通常称为截距或偏置系数。
例如,在简单的回归问题中(单个 x 和单个 y),模型的形式将是
y = B0 + B1*x
在更高维度中,当我们有多个输入 (x) 时,这条线被称为平面或超平面。因此,表示是方程的形式和用于系数的特定值(例如,上面示例中的 B0 和 B1)。
通常会谈论像线性回归这样的回归模型的复杂性。这指的是模型中使用的系数数量。
当一个系数变为零时,它有效地消除了输入变量对模型的影响,从而消除了模型所做的预测(0 * x = 0)。如果你查看正则化方法,这变得相关,这些方法通过对系数的绝对大小施加压力,将一些系数驱动到零来改变学习算法以降低回归模型的复杂性。
现在我们了解了线性回归模型使用的表示,接下来回顾一些从数据中学习这种表示的方法。

什么是线性回归?
图片来源:Estitxu Carton,保留部分权利。
线性回归模型学习
学习线性回归模型意味着使用我们可用的数据来估计表示中使用的系数的值。
在本节中,我们将简要介绍四种准备线性回归模型的技术。这不足以从头开始实现它们,但足以了解所涉及的计算和权衡。
由于该模型研究得如此透彻,因此有更多技术。请注意普通最小二乘法,因为它是普遍使用的最常见方法。还要注意梯度下降法,因为它是机器学习课程中最常教授的技术。
1. 简单线性回归
对于只有一个输入的简单线性回归,我们可以使用统计学来估计系数。
这需要你从数据中计算统计属性,例如均值、标准差、相关性和协方差。所有数据都必须可用于遍历和计算统计数据。
这在 Excel 中作为练习很有趣,但在实践中作用不大。
2. 普通最小二乘法
当我们有多个输入时,我们可以使用普通最小二乘法来估计系数的值。
普通最小二乘法旨在最小化残差平方和。这意味着,给定通过数据的回归线,我们计算每个数据点到回归线的距离,将其平方,并将所有平方误差相加。这就是普通最小二乘法试图最小化的量。
这种方法将数据视为矩阵,并使用线性代数运算来估计系数的最优值。这意味着所有数据都必须可用,并且你必须有足够的内存来容纳数据并执行矩阵运算。
除非作为线性代数练习,否则自己实现普通最小二乘法很不寻常。你更有可能调用线性代数库中的过程。这个过程计算速度非常快。
3. 梯度下降法
当有一个或多个输入时,你可以通过迭代地最小化模型在训练数据上的误差来优化系数的值。
此操作称为梯度下降法,其工作原理是为每个系数设置随机初始值。然后计算每对输入和输出值的平方误差和。使用学习率作为比例因子,并沿最小化误差的方向更新系数。重复此过程,直到达到最小平方误差和或无法进一步改进。
使用此方法时,你必须选择一个学习率 (alpha) 参数,该参数确定每次迭代过程中要采取的改进步长。
梯度下降法常以线性回归模型为例进行讲解,因为它相对容易理解。在实践中,当你的数据集非常大(行数或列数很多)可能无法完全载入内存时,它非常有用。
4. 正则化
线性模型的训练有一些扩展,称为正则化方法。这些方法旨在最小化模型在训练数据上的平方误差和(使用普通最小二乘法),同时还降低模型的复杂性(例如模型中所有系数的数量或绝对大小之和)。
线性回归的两种流行正则化程序示例是:
当输入值存在共线性且普通最小二乘法会使训练数据过拟合时,这些方法非常有效。
现在你了解了学习线性回归模型中系数的一些技术,接下来我们看看如何使用模型对新数据进行预测。
使用线性回归进行预测
鉴于表示是一个线性方程,进行预测就像解决特定输入集的方程一样简单。
让我们通过一个例子具体说明。假设我们根据身高 (x) 预测体重 (y)。此问题的线性回归模型表示将是
y = B0 + B1 * x1
或者
体重 = B0 + B1 * 身高
其中 B0 是偏置系数,B1 是身高列的系数。我们使用一种学习技术来找到一组好的系数。一旦找到,我们可以插入不同的身高值来预测体重。
例如,我们使用 B0 = 0.1 和 B1 = 0.5。让我们将它们代入并计算身高为 182 厘米的人的体重(以千克为单位)。
体重 = 0.1 + 0.5 * 182
体重 = 91.1
你可以看到上面的方程可以绘制成二维平面上的一条直线。无论身高如何,B0 都是我们的起点。我们可以输入从 100 到 250 厘米的一系列身高,将它们代入方程,得到体重值,从而绘制出我们的直线。
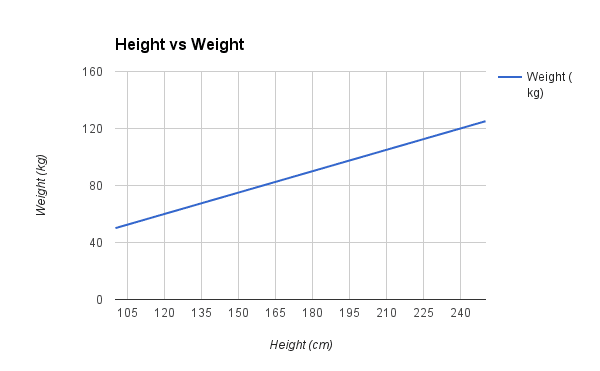
身高与体重线性回归示例
现在我们知道了如何根据学习到的线性回归模型进行预测,接下来我们来看看一些准备数据以充分利用这种模型的经验法则。
为线性回归准备数据
线性回归已被深入研究,有大量文献阐述了数据必须如何构造才能最好地利用该模型。
因此,当谈论这些要求和期望时,有很多复杂的说法,可能会令人望而生畏。实际上,在使用普通最小二乘回归(线性回归最常见的实现方式)时,你可以将这些规则更多地作为经验法则。
尝试使用这些启发式方法对数据进行不同的准备,看看哪种方法最适合你的问题。
- 线性假设。线性回归假设你的输入和输出之间存在线性关系。它不支持任何其他关系。这可能很明显,但在属性很多时记住这一点很有用。你可能需要转换数据以使关系线性化(例如,对指数关系进行对数转换)。
- 去除噪声。线性回归假设你的输入和输出变量没有噪声。考虑使用数据清洗操作,让你更好地暴露和澄清数据中的信号。这对于输出变量最为重要,如果可能,你希望去除输出变量 (y) 中的异常值。
- 去除共线性。当你的输入变量高度相关时,线性回归将使数据过拟合。考虑计算输入数据的成对相关性并去除相关性最高的变量。
- 高斯分布。如果你的输入和输出变量具有高斯分布,线性回归将做出更可靠的预测。你可能会通过对变量进行转换(例如,对数或 BoxCox 转换)来使其分布更像高斯分布而获得一些好处。
- 重新缩放输入:如果你使用标准化或归一化重新缩放输入变量,线性回归通常会做出更可靠的预测。
请参阅维基百科上关于线性回归的文章,其中列出了模型所做的假设。在普通最小二乘法维基百科文章中也有一个很好的假设列表。
从头开始构建线性回归模型
简单线性回归(带一个自变量)的公式为

其中
- y 是因变量(目标),
- x 是自变量(特征),
- m 是直线的斜率(也称为权重或系数),
- b 是 y 轴截距。
为了找到最小化误差的 m 和 b 值,我们可以使用普通最小二乘法。m 和 b 的公式(根据数据点)为
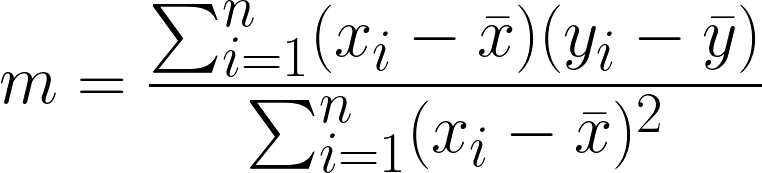
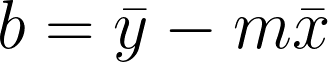
这是上述公式的 Python 实现。我们将使用 Numpy 库来创建训练算法、预测函数、RMSE 函数和样本数据。
- 我们将使用 Numpy 函数将方程转换为 Python,并计算 m 和 b。
- 我们还将创建一个预测和 RMSE 函数,用于分析模型性能。
一旦理解了 Numpy 的基础知识,将数学方程转换为 Python 代码就变得容易了。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
import numpy as np # 计算 m 和 b 的函数 def linear_regression(X, y): x_mean = np.mean(X) y_mean = np.mean(y) numerator = np.sum((X - x_mean) * (y - y_mean)) denominator = np.sum((X - x_mean) ** 2) m = numerator / denominator b = y_mean - (m * x_mean) return m, b # 计算预测的函数 def predict(X, m, b): return m * X + b # 计算 RMSE 的函数 def rmse(y_true, y_pred): return np.sqrt(np.mean((y_true - y_pred) ** 2))</prev> <ol start="3"> <li>我们将通过提供样本数据来训练我们的模型。 <li>进行 预测。 <li>通过使用预测值,计算 RMSE 指标。 </ol> <pre class="lang:default decode:true">X = np.array([7, 8, 10, 12, 15, 18]) Y = np.array([9, 10, 12, 13, 16, 20]) # 训练模型 m, b = linear_regression(X, Y) # 进行预测 predictions = predict(X, m, b) # 计算 RMSE error = rmse(Y, predictions) print("斜率 (m):", m) print("截距 (b):", b) print("预测值:", predictions) print("RMSE:", error) |
输出
我们的预测值与 Y 非常吻合,RMSE 也较低。
|
1 2 3 4 |
斜率 (m): 0.9589552238805968 截距 (b): 2.145522388059705 预测值: [ 8.85820896 9.81716418 11.73507463 13.65298507 16.52985075 19.40671642] RMSE: 0.4440037201224643 |
为了更好地理解我们的结果,我们将使用 Matplotlib 进行可视化。我们将创建数据点的散点图和预测的线图。
|
1 2 3 4 5 6 7 8 9 |
import matplotlib.pyplot as plt plt.scatter(X, Y, color='blue', label='数据点') plt.plot(X, predictions, color='red', label='回归线') plt.xlabel('自变量 X') plt.ylabel('因变量 y') plt.title('线性回归模型') plt.legend() plt.show() |
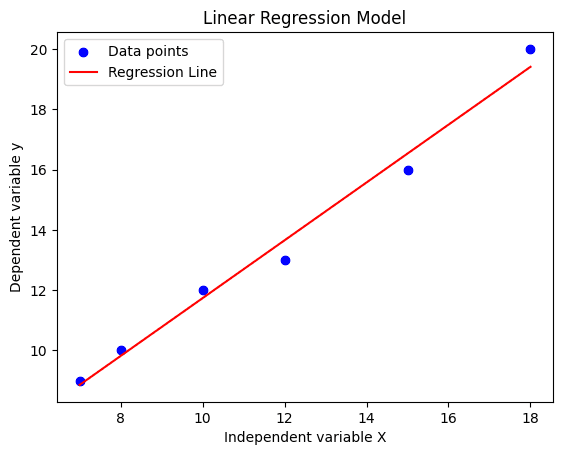
正如我们所见,我们的回归线完美拟合,损失最小。
进一步阅读
关于线性回归,还有很多值得阅读的资料。在进一步阅读之前,先开始使用它吧,当你想要深入研究时,下面是一些你可以使用的参考资料。
提及线性回归的机器学习书籍
这些是一些你可能拥有或可以访问的机器学习书籍,它们在机器学习的背景下描述了线性回归。
- 机器学习初级课程,第一章。
- 统计学习导论:附R应用,第三章。
- 应用预测建模,第六章。
- 机器学习实战,第八章。
- 统计学习要素:数据挖掘、推断和预测,第三章。
关于线性回归的帖子
以下是我遇到的一些关于线性回归的有趣文章和博客文章。
还有没有更多关于线性回归,且侧重于机器学习和预测建模的好资料?请留言告诉我。
总结
在这篇文章中你了解了用于机器学习的线性回归算法。
你涵盖了许多内容,包括
- 描述线性回归模型时常用的名称。
- 模型使用的表示。
- 用于估计模型中系数的学习算法。
- 在使用线性回归准备数据时需要考虑的经验法则。
尝试线性回归并熟悉它。
你对线性回归或这篇文章有什么疑问吗?
请留言提问,我将尽力回答。





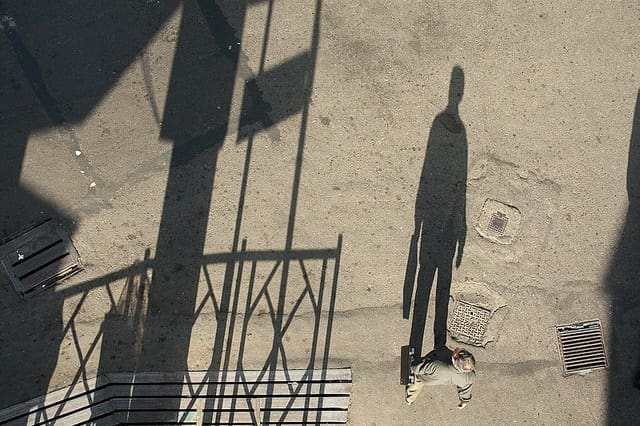
嗨
感谢这篇好文章。
我对线性回归假设有一个疑问。
我觉得在单变量线性回归方程 Y=W0+W1*X+E 中,误差项 E 总是小于 W1*X 项。如果 E > W1*X,则意味着其他变量对因变量 Y 的影响更大。
请指正我的错误。
嗨 Amit,我不确定你的意思。
简单线性回归方程是
如果 E>w1*x,那并不意味着什么。实际上,E 被假定可以取 - 无穷大到 + 无穷大之间的任何值
谢谢。
不客气
y=mx+c
线性回归方程。
这是一条直线的方程。m 是斜率,c 是常数。
是的,没错。谢谢。
嗨 Amith, Jason,
我想 Amith 是想说,关于 n 线性回归的误差是线性方程的一部分吗?如果我错了,请纠正我。
嗨 Jason
这篇文章很好
这帮助我完成了机器学习中的线性回归项目
但我对线性代数的概念仍然感到有点困惑
坚持住。
对线性回归的解释很棒。
谢谢。
有人能解释一下这个算法的时间复杂度吗?
简单线性回归的训练时间复杂度为 O(p^2n+p^3),预测时间复杂度为 O(p)。
感谢分享,Joe。
嗨 Jason,如果每个 X 都有多个 Y 值怎么办?那么为每个 X 找到一个神奇的通用 Y 值是不是胡说八道?例如,每个 X 有 10 个不同的 Y 值,Y 轴上的范围很大。这可能只有在每个 X 只有一个 Y 值,或者多个值彼此接近时才有意义。因为有多个 Y 值,在大多数情况下你永远不会得到正确的 Y。那么简单平均值是不是比尝试用线性回归做一些魔术更好?
如果你的问题是预测一个类别标签,那么你可以使用多标签分类来预测给定 X 的多个 y 值。
嗨 Jason,谢谢你的回复。我刚刚更多地研究了线性回归,现在对我来说更清楚了。我必须提高我不足的数学和统计(当然还有机器学习)技能。所以进展相当缓慢 : )。最近我在研究线性方程时,注意到它和线性回归(斜截式)有相同的公式 : )。相当令人惊讶,但这样线性回归的公式就更熟悉了。谢谢你,祝好,稍后我也会研究类别标签问题。Luky
非常感谢你,Jason。我一直在寻找 Weka 中应用于数据集的线性回归,以获得清晰的理解。你能告诉我哪里可以找到它们,就像你解释波士顿房价数据集那样吗?
这里有一个例子
https://machinelearning.org.cn/regression-machine-learning-tutorial-weka/
谢谢这篇好文章!请问,我在大学做项目需要更多帮助:我需要将(不太难,我不是专家)机器学习算法应用于金融数据集,使用 R 语言。我选择了线性回归,其中资产的每日价格是 y,每日开盘价/最高价/最低价是 x。我只是使用了 lm 命令进行拟合,分析了结果并让模型预测了值。变量显然是相关的,如果我将原始价格绘制在 x 轴上,预测值绘制在 y 轴上,这些点会像一条直线一样延伸。我能得出结论,价格和开盘价/最高价/最低价之间存在线性相关性吗?也许这很明显,但我问是因为我不确定我所做的所有这些是否都正确。
再次感谢,来自意大利的问候 🙂
我这里有一些关于时间序列的帮助,可能有用。
https://machinelearning.org.cn/start-here/#timeseries
你好,
我真的很喜欢你的文章,内容全面但又简单易懂。我正在努力理解机器学习,并且正在观看关于回归的教程。所以我的问题是,对于给定的数据集,在构建模型之前,我是否应该进行特征提取——使用前向选择、后向消除或双向消除?在我获得特征之后,才构建模型,并使用普通最小二乘法来构建模型。我的理解正确吗?我正在寻找一个关于首先做什么的顺序。
谢谢,
山姆
是的,你可以。尝试使用和不使用特征选择,以确保它能提高技能。
嗨,Jason!
感谢这篇精彩的文章总结了主要概念。我只想表达我对一件事的疑问。你确定线性回归假设输入是高斯分布吗?输入应该只提供关于输出分布均值的信息(这是唯一假设的高斯分布)。用数学术语表达就是
Y = beta0 + beta1*X + eps
因为
eps ~ N(0,sigma)
Y|X ~ N(beta0 + beta1*X , sigma)
如你所见,对 X 没有假设。重要的是我们的 X 如何代表我们从中抽取 X 的真实总体,这样我们才能声称 X 和 Y 之间的线性关系在广泛的输入范围内成立。
你觉得呢?
感谢你的评论!
是的,在这里了解更多
https://en.wikipedia.org/wiki/Linear_regression
https://en.wikipedia.org/wiki/Ordinary_least_squares
在第一个链接的假设部分…
“弱外生性。这本质上意味着预测变量 x 可以被视为固定值,而不是随机变量。这意味着,例如,预测变量被假定为无误差的——也就是说,没有被测量误差污染。尽管这个假设在许多情况下不现实,但放弃它会导致显著更困难的误差变量模型。”
不错。
你好,
在回归问题中
如果我在数据中拟合了一条线,这意味着值 Y 和其他特征之间存在线性关系。
现在,我们还能得出什么结论?高权重特征与值 Y 有相似之处的可能性是否存在?
假设我有三个特征 A、B 和 C,而权重用 W 表示。我提出了以下假设,
假设 = 偏差 + A*W1 + B*W2 + C*W3 + A^2*W4
上面的假设正确吗?还是我需要将每个特征都设为二次方?像这样,
假设 = 偏差 + A*W1 + B*W2 + C*W3 + A^2*W4 + B^2*W5 + C^2*W6
请说明为什么其中一个或两个都正确?
不,你可以混合使用正常输入和平方输入。
我建议仔细实验,看看哪种方法最适合你的特定数据。
如果我错了请纠正我…但是所有训练/创建/制作/拟合模型到数据集的方法都与最小化平方误差函数有关吗?
方法 1 我相信也最小化了 SSE,但使用了统计学。
方法 2 最小化 SSE
方法 3 最小化多变量函数的 SSE
方法 4 在附加约束下最小化 SSE
我错了吗?
方法 1:https://en.wikipedia.org/wiki/Simple_linear_regression#Fitting_the_regression_line
线性回归问题的以下数据
X. Y
2104. 460
1416. 232
1534. 314
852. 178
以下哪组值将使训练样本的误差最小?
1. m=4, c=300
2. m=5, c=30
这是家庭作业问题吗?
哪本书适合深入学习线性回归?
任何好的机器学习教科书。
我在这里列出了一些书
https://machinelearning.org.cn/faq/single-faq/what-other-machine-learning-books-do-you-recommend
我如何或从哪里获得 B0 和 B1 的值?我是初学者。
算法将估计它们,从示例中学习它们。
例如,在 scikit-learn 等库中实现的算法。
你好 jason,
谢谢。
“线性”回归这个词术语经常被误用(由于语言问题)。例如,我可以使用(当然)线性回归来处理多项式自变量 (x) 的因变量 (Y)。如何做到?通过添加更多层和输出层的“relu”激活函数,我计算了三次、二次和一些其他多项式(Y=x^3,或 Y = x^2,等等)。
但如果你想更“正统”或规范,你只需在输入中添加更多特征,例如 X^2(作为当前 x 特征的新输入特征),等等……所以显然线性表达式只意味着所有特征都相加(beta0 * x + beta1*X^2 +…),这就是线性的全部含义……所以它能实现非线性依赖 Y= f(x) 依赖关系。你的看法如何?
致敬
非常感谢你的所有教程!
向线性模型添加输入变量的非线性变换仍然意味着模型是线性的。它仍然是输入值的加权和。
你可以选择在变换中还是在模型中管理复杂性。
好的。谢谢
好文章,非常感谢,我对机器学习应用更感兴趣。请提供参考资料,如书籍或网页链接,谢谢
我有很多应用示例。你具体在寻找什么?
在“使用线性回归进行预测”部分有一个错误。
“weight = 0.1 + 0.05 * 182”中应该是 0.5 而不是 0.05
谢谢,已修正。
嘿,你能指导我如何处理 # 带有 x 和 y 的训练数据,即一维数据 x 和标签 y 吗?
应该使用哪种方法??
抱歉,我不明白,你能详细说明一下吗?
嘿 ,
我想问一下哪种数据集对线性回归最好,哪种最差?另外,你能推荐一些关于其他算法(如逻辑回归和 SVM)类似理论信息的书籍或文章吗?
谢谢
输入和输出之间存在线性关系的数据集非常适合线性回归。
具有非线性关系的数据集可能不适合。
我读了上面的文章,写得很好。先生,要从头开始实现线性回归算法,需要多少知识?
无需任何先验知识,直接开始吧!
https://scholarworks.umass.edu/cgi/viewcontent.cgi?article=1308&context=pare
您写道,线性回归将“变量的正态性”视为一个假设。但上述研究工作表明这是一个误解,真正需要的是残差误差的正态性。请您核实一下。
听起来很对。
你好,我有一条满足数据的线性线,但问题是我在同一个图中画了两条不同的线,如何解决这个问题
我无法在这里上传那个图,你能提供我其他方式来分享我得到的图吗
我想你指的是多目标或多输出回归。
这个可能会有帮助
https://scikit-learn.cn/stable/modules/generated/sklearn.multioutput.MultiOutputRegressor.html
嗨,Jason,
我有一个关于线性模型的问题:假设我们有多个变量,并想把它们输入到线性模型中。我看到有些人将所有变量作为输入并同时放入模型中;我还看到有些人每次只测试并将一个变量放入线性模型中,然后对每个变量逐个运行模型。我对这两种选项之间的区别感到困惑,尽管这两种选项都可以得出 p 值(第二种需要进行多次校正)和系数,但我认为这两种方法的结果是不同的。你能给我解释一下吗?提前谢谢你!
通常,所有相关变量都作为输入提供给模型并用于进行预测。
明白了,谢谢你 Jason!
不客气。
嗨,Jason,
我有一个关于多元线性回归的问题。
这是我的部分代码
from sklearn.model_selection import train_test_split
train_X,test_X,train_y,test_y = train_test_split(X,y,test_size = 0.33 ,random_state=42)
reg = LinearRegression()
model = reg.fit(train_X,train_y)
predictions = model.predict(test_X)
print(“r2_score : %.2f” % r2_score(test_y,predictions))
print(“Mean_squared_error : %.2f ” % mean_squared_error(test_y,predictions))
for i in range(0,3)
print(“model parameters : %.2f” % model.coef_[i])
print(“model intercept : %.2f” % model.intercept_)
plt.scatter(test_X.TV,test_y)
plt.plot(test_X.TV,predictions)
plt.show()
plt.scatter(test_X.radio,test_y)
plt.plot(test_X.radio,predictions)
plt.show()
plt.scatter(test_X.newspaper,test_y)
plt.plot(test_X.newspaper,predictions)
plt.show()
问题是我想要这样做
plt.scatter(test_X.TV,test_y)
plt.plot(test_X.TV,predictions)
plt.show()
但是,我得到了一个错误“x 和 y 的大小必须相同”,肯定是因为 X 是三维的而 y 是一维的,即使我将 X 展平,也会得到一个错误。我该怎么做才能绘制出类似上面的图表?
谢谢你的帮助
抱歉,我无法调试你的代码示例,也许这会有帮助。
https://machinelearning.org.cn/faq/single-faq/can-you-read-review-or-debug-my-code
在机器学习中,我们是需要检查训练数据还是完整数据集的假设?谢谢!
理想情况下,是的,但有时如果我们忽略算法的要求,也能达到良好/最佳性能。
所以,是也不是。
我特别不想写这个,但是,作为一名博士,你应该能够写出语法和机械结构都正确的英语。不幸的是,你非常需要改进写作的机械结构(尤其是逗号结构)。我确实很感谢你试图提供有用的信息,但从学术角度来看,这里的基本标点符号简直糟糕透顶。你不在乎这个吗?抱歉语气严厉,但懒得用连贯的形式表达你的想法,这表明你对读者、我们的语言和你自己的思想缺乏尊重。如果你不表现出这种尊重,那么那些更懂行的人也很不可能回报你任何尊重。
看看这一段,告诉我你看不出两个句子中的主要标点错误。(如果你真的不知道,用逗号对分隔非必要子句是逗号用法的基本规则,而你完全忽略了它。)整篇文章都是这样。
“机器学习,更具体地说是预测建模领域[需要逗号]主要关注于最小化模型误差或尽可能做出最准确的预测,而牺牲可解释性。在应用机器学习中,我们将借鉴、重用和“窃取”来自许多不同领域的算法,包括统计学[需要逗号]并将其用于这些目的。”
显然每个人都会犯错,但反复犯这种基本错误,要么是缺乏理解,要么是完全无视。我真诚地希望一位博士能努力不沦落到如今网上常见的像高中生胡言乱语的水平。如果你选择成为一名学者,如果你能努力保持一定的学术严谨性,而不是助长我们书面语言的退化,那么同行学者们一定会感激不尽。如果你难以识别基本的标点错误,你可以阅读一本关于它的书。任何能完成博士课程的人肯定都能做到这一点。
感谢你坦诚的反馈。研究科学家也是人。
我聘请了一个编辑团队来审阅所有新的教程。希望他们的标准更高。
我数学很差,背景是市场营销……我需要多长时间才能学习线性回归中的复杂概念?
你可以立即通过 Weka 开始使用它
https://machinelearning.org.cn/start-here/#weka
嗨,Jason,
假设我有一个数据集,其中3个特征高度相关,相关系数约为0.8。这些特征也与目标高度相关。
如果我删除其中一个特征,我将解决多重共线性问题。然而,这难道不会导致遗漏变量偏差,从而导致内生性吗?
如何在没有内生性和避免多重共线性之间取得平衡?
也许可以尝试依次删除每个变量,并评估其对模型的影响。使用能够产生最佳预测性能的组合。
好文章。
我们应该在回归方程中写 y-hat 而不是 y,对吗?因为它是一个预测值。
当然可以。
嗨,Jason,
非常感谢这篇好文章。我能问一个关于回归系数的问题吗?我正在尝试构建一个多元回归模型,我想用一组已知值来实际建模系数或参数。这可行吗?例如 y(u,v,t)=f0+f1(u, v, t)*x1+f2(u, v, t)*x2+…+fn(u,v,t)*xn+误差项,其中 u, v, 和 t 是已知值,我的目标是找到模型 f1, f2… fn 来最小化损失函数。
如果我没有表达清楚,请原谅。非常感谢你的帮助!
祝好,
程璧
不客气。
是的,如果你有固定值和未知值,那么你可以使用优化算法来找到最小化误差的未知值。梯度下降可能是一个好的开始。
谁能帮我回答这个问题?
线性回归分类器在 sklearn 中所在的类的名称是什么?
线性回归不能用于分类。
它是一种用于预测数值的“回归”算法
https://scikit-learn.cn/stable/modules/generated/sklearn.linear_model.LinearRegression.html
一篇非常好的文章,真的很有用
谢谢!
好文章,信息量大
谢谢。
嘿,好文章
我是一名电气工程师,在我的论文中,我想用粘土制作低密度聚乙烯作为电绝缘材料。
我制作了7个粘土含量在0%到15%之间的样品。
我已经对它进行了测试(电气和机械)。
我想使用机器学习来确定我制作的样品中最佳粘土含量,甚至是我没有制作的含量。
有什么建议我应该从哪里开始?
提前感谢
谢谢。
也许这个过程会帮助您完成您的项目
https://machinelearning.org.cn/start-here/#process
好文章,信息量大
谢谢。
认知偏差类型还有很多很多,但我会将我的文章限制在这四种最重要的类型。
谢谢。
好的信息和知识
谢谢。
这真是棒极了的培训。
谢谢!
嗨,Jason,
感谢这篇文章。
我只有一个问题:这些数据假设是统计线性回归的要求,在机器学习线性回归中可以忽略吗?我想说,在机器学习中,使用这个模型的唯一要求是输入和输出之间存在线性关系。我 HTH统计要求被忽略是由于更注重预测性而不是可解释性。
预测性优先,如果你可以通过打破规则/假设获得更好的结果,那么就这样做吧。
解释得很好,各位也可以看看这篇关于线性回归的博客 https://mindmajix.com/linear-regression
感谢分享。
非常棒且信息丰富的培训。
谢谢你。很高兴你喜欢。
感谢分享
谢谢。希望你喜欢。
这是一篇信息量很大的文章,非常感谢,对我很有帮助
谢谢分享,乔
大家好,
感谢这篇文章。我有一个问题。如果我只有两个或更少的特征,使用什么样的非线性算法比较好?我说的非线性并不是指多项式。我确实希望我的模型能够学习数据中的特定模式。而且这种模式看起来像随机信号。
您是想用参数模型还是非参数模型?我们可能需要一个参数模型,否则就难以处理。这意味着,我们假设数据的一些特性(例如,多项式),然后估计参数(例如,多项式的系数)。如果不做任何假设,就很难做到。
我仔细阅读了您的文章。这真是一篇信息量很大的文章。请继续发布像这样信息量大的文章。谢谢。
谢谢。很高兴你喜欢。
精彩而详细。非常好。
你好,我是机器学习新手。我正在学习线性回归算法。我有一个疑问,就是在成本函数中,我们将SSE除以1/2m。我明白1/2在梯度下降的参数计算中会抵消,但是为什么1/m会出现在成本函数中呢?
另外,如果我不包含它,可以吗?
你好...这个因子有助于建立一个平均值。
好吧,平均值有什么帮助呢?
请详细解释一下。另外,如果我们不包含1/m,会出现什么问题。
你好,我是机器学习新手。在学习线性回归的成本函数时,我了解到 J(theta) = 1/2m 求和(h(theta(i)) - y(i))^2
其中 m 是训练样本的总数
取 1/2 是为了简化计算吗?
我的问题是,我们正在对 SSE 进行求和,然后除以训练样本的数量 (m)。
那么,我们为什么要除以 m 来求平均值呢?
我们不能直接计算误差项的总和(而不除以 m),这样我们就得到了需要通过寻找最优 theta 值来最小化的总误差,然后我们的工作就完成了吗?
请详细解释一下,因为我试图在很多地方找到答案,但没有找到满意的答案,而且在讲座中,教授也没有澄清这个疑问。有些人回答了,但无法证明。我问他们无论如何会造成什么不同?
另外,请附上一些我可以进一步阅读的资源。谢谢。
我仔细阅读了您的文章。这真是一篇信息量大且有用的文章。请继续发布此类信息丰富的文章。谢谢。
很棒的反馈,Ivy!继续努力!
内容非常有帮助,易于理解
谢谢您的反馈,Arpita!
你好,
完成 Salesforce 在线培训后,我正在学习机器学习。我发现这篇文章对我很有帮助。我的问题是,我可以在 Salesforce 中使用机器学习吗?
任何建议都将不胜感激。
你好,James...请详细说明您使用机器学习模型的目标,以便我们更好地帮助您。
好建议。
感谢您的反馈和支持,Anny!我们非常感激!
感谢您分享这篇关于机器学习线性回归的信息丰富的文章。对于机器学习新手,想要了解更多线性回归的人来说,这是一个极好的资源。
文章对线性回归进行了清晰简洁的介绍,用简单的术语解释了概念,并提供了示例帮助读者更好地理解这个主题。作者还介绍了不同类型的线性回归模型,包括简单线性回归、多元线性回归和多项式回归,这对于希望将这项技术应用于实际问题的读者来说很有帮助。
谢谢 Donald 的精彩反馈!我们非常感谢。