在这篇文章中，您将发现 4 个用于 R 平台的线性回归食谱。
您可以复制代码并粘贴到文章中，以快速开始您自己的项目，或在 R 中学习和实践线性回归。
通过我的新书 《R 机器学习精通》快速启动您的项目，其中包括分步教程和所有示例的R 源代码文件。
让我们开始吧。
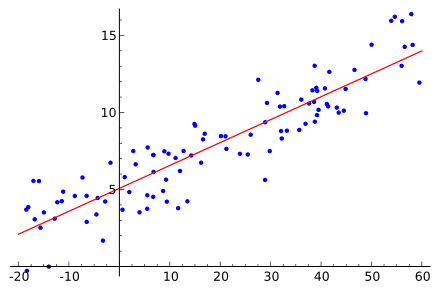
普通最小二乘回归
部分权利保留
本文中的每个示例都使用了 R 自带的 datasets 包中提供的 longley 数据集。longley 数据集描述了从 1947 年到 1962 年观察到的 7 个经济变量，用于预测每年的就业人数。
普通最小二乘回归
普通最小二乘 (OLS) 回归是一种线性模型，它试图找到一组用于直线/超平面的系数，以最小化误差平方和。
|
1 2 3 4 5 6 7 8 9 10 11 |
# 加载数据 data(longley) # 拟合模型 fit <- lm(Employed~., longley) # 总结拟合 summary(fit) # 进行预测 predictions <- predict(fit, longley) # 总结准确度 mse <- mean((longley$Employed - predictions)^2) print(mse) |
详细了解 lm 函数和 stats 包。
需要更多关于R机器学习的帮助吗？
参加我为期14天的免费电子邮件课程，了解如何在您的项目中使用R（附带示例代码）。
点击注册，同时获得该课程的免费PDF电子书版本。
逐步线性回归
逐步线性回归是一种方法，它利用线性回归来发现数据集中哪些属性子集能产生最佳模型。它是逐步的，因为该方法的每次迭代都会对属性集进行更改，并创建一个模型来评估该集的性能。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
# 加载数据 data(longley) # 拟合模型 base <- lm(Employed~., longley) # 总结拟合 summary(base) # 执行逐步特征选择 fit <- step(base) # 总结选定的模型 summary(fit) # 进行预测 predictions <- predict(fit, longley) # 总结准确度 mse <- mean((longley$Employed - predictions)^2) print(mse) |
详细了解 step 函数和 stats 包。
主成分回归
主成分回归 (PCR) 通过主成分分析 (PCA) 的输出来创建一个线性回归模型来估计模型的系数。当数据具有高度相关的预测变量时，PCR 非常有用。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
# 加载包 library(pls) # 加载数据 data(longley) # 拟合模型 fit <- pcr(Employed~., data=longley, validation="CV") # 总结拟合 summary(fit) # 进行预测 predictions <- predict(fit, longley, ncomp=6) # 总结准确度 mse <- mean((longley$Employed - predictions)^2) print(mse) |
详细了解 pcr 函数和 pls 包。
偏最小二乘回归
偏最小二乘 (PLS) 回归创建一个模型，该模型基于问题空间的转换投影中的数据。与 PCR 一样，PLS 适用于具有高度相关的预测变量的数据。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
# 加载包 library(pls) # 加载数据 data(longley) # 拟合模型 fit <- plsr(Employed~., data=longley, validation="CV") # 总结拟合 summary(fit) # 进行预测 predictions <- predict(fit, longley, ncomp=6) # 总结准确度 mse <- mean((longley$Employed - predictions)^2) print(mse) |
详细了解 plsr 函数和 pls 包。
总结
在这篇文章中，您学习了 4 个在 R 中创建线性回归模型并使用这些模型进行预测的食谱。
Kuhn 和 Johnson 的《应用预测建模》第 6 章为初学者提供了 R 线性回归的出色入门。Faraway 的《R 中的实用回归和方差分析》（PDF）提供了更深入的讲解。
在R中发现更快的机器学习！
在几分钟内开发您自己的模型
...只需几行R代码
在我的新电子书中探索如何实现
精通 R 语言机器学习
涵盖自学教程和端到端项目，例如
加载数据、可视化、构建模型、调优等等...
最终将机器学习应用到您自己的项目中
跳过学术理论。只看结果。
SLR 的表现不如 OLSR 有什么原因吗？再次，问题在于如何判断“更好”。我注意到 rmse(SLR) > rmse(OLSR)。如果我们旨在获得更好的拟合，rmse 应该会下降吗？
我认为 rmse 计算步骤缺少了平方根。
rmse <- sqrt( mean((longley$Employed – predictions)^2) )
是的，谢谢，这是我注意到的问题，但不确定。
Jason 计算的是 mse 而不是 rmse。所以没有平方根。
有人可以确认/反驳我的理解吗？以下属性是否由“逐步线性回归”算法确定为最佳？
GNP + Unemployed + Armed.Forces + Year
我们无法知道哪种算法最适合您的数据，请尝试一套方法并比较每种方法的技能。
请看这篇文章
https://machinelearning.org.cn/a-data-driven-approach-to-machine-learning/
抱歉，我说得不清楚。我并不是在问哪种算法最好。我只是在运行上面关于“逐步线性回归”的示例代码。然后我正在尝试理解屏幕上打印的内容。（因此数据是“longley”。）
我看到执行了三个步骤/迭代。
我的理解
1. 第一轮迭代后，“GNP.deflator”被丢弃，因为其 AIC 最低 (-35.163)
2. 第二轮迭代后，“Population”被丢弃，因为其 AIC 最低 (-36.799)
3. 第三步后，“GNP”应该被丢弃。（其 AIC 为 -31.879）
我的理解正确吗？
啊，我明白了。结果是为最终模型建议或选择的变量。