用于机器学习的梯度下降线性回归教程

随机梯度下降是机器学习中一种重要且广泛使用的算法。

在本帖中，您将了解如何通过最小化训练数据集上的误差来使用随机梯度下降为简单的线性回归模型学习系数。

阅读本文后，您将了解

• 简单线性回归模型的形式。
• 梯度下降与随机梯度下降的区别
• 如何使用随机梯度下降学习简单的线性回归模型。

通过我的新书《精通机器学习算法》来启动您的项目，其中包含分步教程以及所有示例的Excel电子表格文件。

让我们开始吧。

• 2021年2月更新：修正了预测值中的拼写错误。

用于机器学习的梯度下降线性回归教程
照片由Stig Nygaard拍摄，部分权利保留。

教程数据集

我们使用的数据集是完全虚构的。

这是原始数据。属性 x 是输入变量，y 是我们要预测的输出变量。如果我们获得更多数据，我们将只有 x 值，并且我们会对预测 y 值感兴趣。

下面是 x 与 y 的简单散点图。

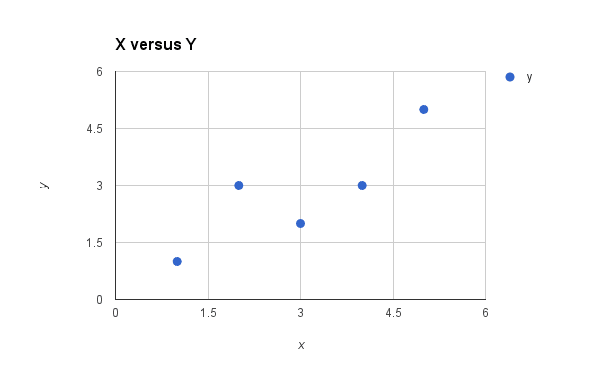
用于简单线性回归的数据集图

我们可以看到 x 和 y 之间的关系有点线性。也就是说，我们可能可以在图的左下角到右上角画一条对角线来大致描述数据之间的关系。这表明对这个小数据集使用线性回归可能是合适的。

获取您的免费算法思维导图

方便的机器学习算法思维导图样本。

我创建了一份方便的思维导图，其中包含60多种按类型组织的算法。

下载、打印并使用它。

简单线性回归

当我们只有一个输入属性（x）并想使用线性回归时，这被称为简单线性回归。

使用简单线性回归，我们希望按如下方式建模数据

y = B0 + B1 * x

这是一条线，其中 y 是我们想要预测的输出变量，x 是我们已知的输入变量，B0 和 B1 是我们需要估计的系数。

B0 被称为截距，因为它决定了线在 y 轴上的截距。在机器学习中，我们可以称之为偏差，因为它会加到我们进行的所有预测上。B1 项被称为斜率，因为它定义了线的斜率，或者 x 在我们添加偏差之前如何转换为 y 值。

该模型被称为简单线性回归，因为它只有一个输入变量（x）。如果存在更多输入变量（例如 x1、x2 等），则称为多元回归。

随机梯度下降

梯度下降是通过沿着成本函数的梯度来最小化函数的过程。

这涉及知道成本的形式以及其导数，以便从给定点知道梯度并可以朝该方向移动，例如朝向最小值向下移动。

在机器学习中，我们可以使用一种称为随机梯度下降的类似技术来最小化模型在训练数据上的误差。

其工作原理是每个训练实例一次仅展示给模型。模型对训练实例进行预测，计算误差，并更新模型以减少下一次预测的误差。

此过程可用于查找模型中导致模型在训练数据上误差最小的系数集。每次迭代，系数（在机器学习语言中称为权重 w）都会使用以下方程进行更新

w = w – alpha * delta

其中 w 是正在优化的系数或权重，alpha 是您必须配置的学习率（例如 0.1），gradient 是模型在训练数据上归因于该权重的误差。

使用随机梯度下降进行简单线性回归

简单线性回归中使用的系数可以通过随机梯度下降找到。

线性回归是一个线性系统，系数可以通过线性代数进行解析计算。在实践中（在大多数情况下），随机梯度下降不用于计算线性回归的系数。

线性回归为学习随机梯度下降提供了一个有用的练习，随机梯度下降是机器学习算法通过最小化成本函数来使用的重要算法。

如上所述，我们的线性回归模型定义如下

y = B0 + B1 * x

梯度下降迭代 #1

让我们从两个系数的值都为 0.0 开始。

B0 = 0.0

B1 = 0.0

y = 0.0 + 0.0 * x

我们可以按如下方式计算预测误差

error = p(i) – y(i)

其中 p(i) 是我们数据集中第 i 个实例的预测值，y(i) 是数据集中第 i 个实例的第 i 个输出变量。

现在，我们可以使用我们起始系数为第一个训练实例计算 y 的预测值

x=1, y=1

p(i) = 0.0 + 0.0 * 1

p(i) = 0

使用预测输出，我们可以计算我们的误差

error = 0 – 1

error = -1

我们现在可以在梯度下降方程中使用此误差来更新权重。我们将从更新截距开始，因为它更容易。

我们可以说 B0 应该对所有误差负责。也就是说，更新权重将仅使用误差作为梯度。我们可以按如下方式计算 B0 系数的更新

B0(t+1) = B0(t) – alpha * error

其中 B0(t+1) 是我们将在下一个训练实例中使用的更新后的系数，B0(t) 是 B0 的当前值，alpha 是我们的学习率，error 是我们为训练实例计算的误差。让我们使用 0.01 的小学习率，并将值代入方程以计算 B0 的新且略有优化的值

B0(t+1) = 0.0 – 0.01 * -1.0

B0(t+1) = 0.01

现在，让我们看看更新 B1 的值。我们使用相同的方程，只是有一个小的变化。误差会根据导致它的输入进行过滤。我们可以使用以下方程更新 B1

B1(t+1) = B1(t) – alpha * error * x

其中 B1(t+1) 是更新后的系数，B1(t) 是当前版本的系数，alpha 是上面描述的相同学习率，error 是上面计算的相同误差，x 是输入值。

我们可以将我们的数字代入方程并计算 B1 的更新值

B1(t+1) = 0.0 – 0.01 * -1 * 1

B1(t+1) = 0.01

我们刚刚完成了梯度下降的第一次迭代，并将权重更新为 B0=0.01 和 B1=0.01。此过程必须对我们数据集中的其余 4 个实例重复。

一次通过训练数据集称为一个 epoch。

梯度下降迭代 #20

我们跳到后面。

您可以再重复此过程 19 次。这是训练数据暴露给模型并更新系数的 4 个完整 epoch。

这是您应该看到的 20 次迭代中所有系数值的列表

我认为 20 次迭代或 4 个 epoch 是一个不错的整数，也是一个可以停止的好地方。如果您愿意，可以继续。

您的值应该非常接近，但由于不同的电子表格程序和不同的精度，可能会略有差异。您可以将每对系数重新代入简单线性回归方程。这很有用，因为我们可以为每个训练实例计算一个预测，进而计算误差。

下图显示了随着学习过程的进行，每个系数集的误差。这是一个有用的图，因为它表明误差随着每次迭代而减小，并在最后开始有一些波动。

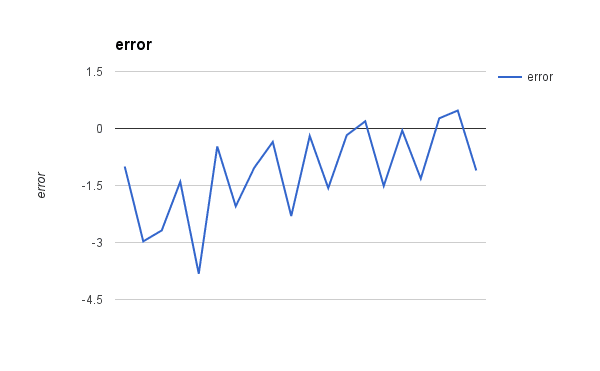
线性回归梯度下降误差与迭代次数的关系

您可以看到，我们的最终系数值为 B0=0.230897491 和 B1=0.7904386102

让我们将它们代入我们的简单线性回归模型，并为我们训练数据集中的每个点进行预测。

我们可以再次绘制数据集，并叠加这些预测（x vs y 和 x vs prediction）。通过 5 个预测值画一条线，可以让我们大致了解模型与训练数据的拟合程度。

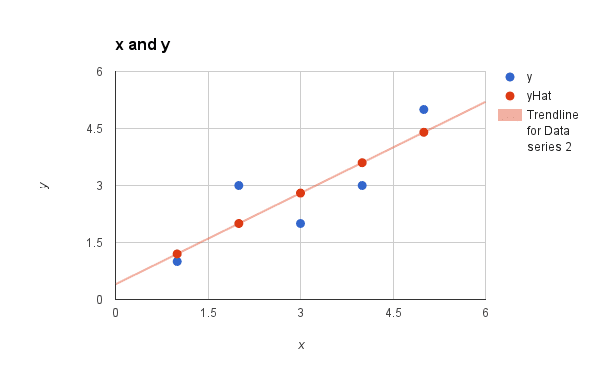
简单线性回归模型

总结

在本帖中，您了解了简单线性回归模型以及如何使用随机梯度下降对其进行训练。

您完成了梯度下降更新规则的应用。您还学习了如何使用学习到的线性回归模型进行预测。

您对这篇帖子或随机梯度下降的简单线性回归有任何疑问吗？请留言提问，我会尽力回答。

了解机器学习算法的工作原理！

几分钟内了解算法如何工作

...只需算术和简单示例

在我的新电子书中探索如何实现
精通机器学习算法

它涵盖了**10种顶级算法**的**解释**和**示例**，例如：
_线性回归_、_k-近邻_、_支持向量机_等等...

最后，揭开
机器学习算法的神秘面纱

跳过学术理论。只看结果。

查看内容