逻辑回归是机器学习从统计学领域借鉴的另一种技术。
它是二元分类问题(具有两个类别值的问题)的首选方法。在这篇文章中,您将了解机器学习的逻辑回归算法。
阅读本文后,您将了解
- 描述逻辑回归时使用的许多名称和术语(如对数几率和 logit)。
- 用于逻辑回归模型的表示。
- 用于从数据中学习逻辑回归模型系数的技术。
- 如何使用学习到的逻辑回归模型实际进行预测。
- 如果您想深入了解,可以去哪里获取更多信息。
- 算法面临的问题和最新解决方案。
- 机器学习和深度学习框架的最新更新。
- 逻辑回归与 XAI。
- 逻辑回归与联邦学习。
这篇文章是为对应用机器学习,特别是预测建模感兴趣的开发人员撰写的。您不需要线性代数或统计学背景。
更新于 2023 年 12 月
- 更新了现有章节以提高清晰度
- 添加章节:算法的主要问题
- 添加章节:知名框架的逻辑回归更新
- 添加章节:逻辑回归:在可解释人工智能和低资源/联邦环境中的多功能性
使用我的新书《精通机器学习算法》,其中包括分步教程和所有示例的Excel 电子表格,来快速启动您的项目。
让我们开始吧。

逻辑回归的学习算法
照片由 Michael Vadon 拍摄,保留部分权利。
逻辑函数
逻辑回归的名字来源于其核心使用的函数——逻辑函数。
该逻辑函数,也称为 sigmoid 函数,是由统计学家开发的,用于描述生态学中人口增长的特性,即快速增长并在达到环境的承载能力时饱和。它是一个 S 形曲线,可以将任何实数值映射到 0 和 1 之间的值,但永远不会精确地等于这些极限。
1 / (1 + e^-值)
其中 e 是自然对数的底(欧拉数,或您的电子表格中的 EXP() 函数),而值是您想要转换的实际数值。下面是使用逻辑函数将 -5 到 5 之间的数字转换到 0 到 1 范围的图。
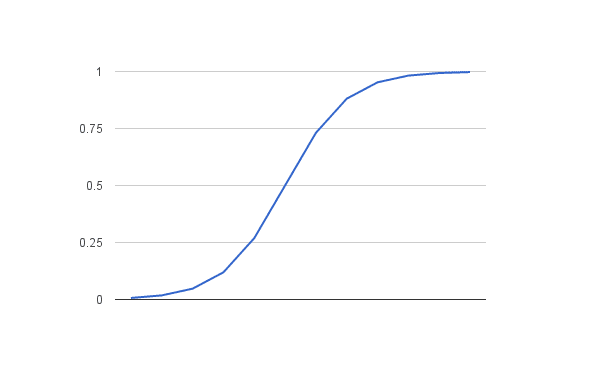
逻辑函数
现在我们知道了逻辑函数是什么,让我们看看它在逻辑回归中是如何使用的。
逻辑回归使用的表示
逻辑回归像线性回归一样,使用一个方程作为表示。
输入值(x)使用权重或系数(称为希腊大写字母 Beta)进行线性组合,以预测输出值(y)。与线性回归的一个关键区别是,被建模的输出值是一个二元值(0 或 1),而不是一个数值。
下面是一个示例逻辑回归方程
y = e^(b0 + b1*x) / (1 + e^(b0 + b1*x))
其中 y 是预测输出,b0 是截距或常数项,b1 是单个输入值(x)的系数。您的输入数据中的每一列都有一个相关的 b 系数(一个常数实数值),必须从您的训练数据中学习。
模型实际在内存或文件中存储的表示是方程中的系数(beta 值或 b 值)。
获取您的免费算法思维导图
方便的机器学习算法思维导图样本。
我创建了一份方便的思维导图,其中包含60多种按类型组织的算法。
下载、打印并使用它。
还可以独家访问机器学习算法电子邮件迷你课程。
逻辑回归预测概率(技术插曲)
逻辑回归模型化了默认类(例如,第一个类别)的概率。例如,如果我们根据身高来建模人的性别为男性或女性,那么第一个类别可以是男性,逻辑回归模型可以写为给定身高的男性的概率,或者更正式地说
P(性别=男性|身高)
在当今的机器学习应用中,理解概率估计至关重要。逻辑回归预测概率,这是分类任务的基础。
换一种说法,我们正在对输入(X)属于默认类别(Y=1)的概率进行建模,我们可以正式地将其写为
P(X) = P(Y=1|X)
需要强调的是,逻辑回归不仅仅是一个分类算法;它是一种估计概率的方法。
我们是在预测概率吗?我以为逻辑回归是分类算法。
逻辑回归是一种强大的分类技术,通过估计输入属于某个类别的可能性来工作。这种估计本质上是概率预测,为了进行类别预测,必须将其转换为二元值(0 或 1)。我们将在稍后讨论预测时更深入地探讨这个过程。
逻辑回归是一种线性方法,但预测是通过逻辑函数转换的。其影响是我们不能再像线性回归那样将预测理解为输入的线性组合。例如,从上面继续,模型可以表述为
p(X) = e^(b0 + b1*X) / (1 + e^(b0 + b1*X))
我不想深入太多数学,但我们可以将上述方程倒过来,如下所示(记住,我们可以通过在另一侧添加自然对数(ln)来从一侧消除 e)
ln(p(X) / 1 – p(X)) = b0 + b1 * X
这个数学转换使我们能够更直观地解释模型。左侧表示对数几率或 probit,这是逻辑回归中的一个关键概念。
这很有用,因为我们可以看到右侧输出的计算再次是线性的(就像线性回归一样),而左侧的输入是对默认类概率的对数。
左侧的这个比率称为默认类的几率(我们使用几率是历史原因,例如,在赛马中通常使用几率而不是概率)。几率计算为事件概率除以非事件概率的比率,例如 0.8 / (1-0.8),其几率为 4。所以我们可以写成
ln(几率) = b0 + b1 * X
由于几率是经过对数转换的,我们将左侧称为对数几率或 probit。可以使用其他类型的函数进行转换(超出范围),但因此,通常将将线性回归方程与概率相关联的转换称为链接函数,例如 probit 链接函数。
我们可以将指数移回右侧,并写成
几率 = e^(b0 + b1 * X)
所有这些都为理解逻辑回归的内部工作原理提供了宝贵的见解,表明模型确实是输入的线性组合。但是,这种线性组合与默认类的对数几率有关,使其成为概率分类的强大工具。
学习逻辑回归模型
逻辑回归算法的系数(Beta 值 b)必须从您的训练数据中估计。这是使用最大似然估计完成的。
最大似然估计是一种许多机器学习算法使用的通用学习算法,尽管它确实假定了您数据的分布(当谈论准备数据时,我们将详细介绍)。
最佳系数将产生一个模型,该模型将为默认类别预测接近 1 的值(例如男性),为其他类别预测接近 0 的值(例如女性)。逻辑回归的最大似然直觉是,搜索过程寻找系数(Beta 值)的值,这些值可以最小化模型预测的概率与数据中(例如,如果数据是主要类别,则概率为 1)的概率之间的误差。
我们不会深入研究最大似然的数学。说一个最小化算法用于优化您的训练数据的最佳系数就足够了。在实践中,逻辑回归模型的优化通常使用高效的数值优化算法来实现,例如有限内存BFGS(L-BFGS)和自适应矩估计(ADAM),这些算法被认为是最佳实践。这些方法提供了更快的收敛性和更高的效率,尤其是在处理大型数据集时。
在学习逻辑回归时,您可以使用更简单的梯度下降算法自己从头开始实现它。

机器学习的逻辑回归
照片由 woodleywonderworks 拍摄,保留部分权利。
使用逻辑回归进行预测
使用逻辑回归模型进行预测就像将数字代入逻辑回归方程并计算结果一样简单。
让我们通过一个具体的例子来说明。
假设我们有一个可以根据身高预测一个人是男性还是女性的模型(完全虚构)。给定身高 150 厘米,这个人是男性还是女性?
我们已经学习了系数 b0 = -100 和 b1 = 0.6。使用上面的方程,我们可以计算身高为 150 厘米时是男性的概率,或者更正式地说 P(男性|身高=150)。我们将使用 EXP() 来表示 e,因为如果您在电子表格中输入此示例,就可以使用它。
y = e^(b0 + b1*X) / (1 + e^(b0 + b1*X))
y = exp(-100 + 0.6*150) / (1 + EXP(-100 + 0.6*X))
y = 0.0000453978687
或者一个人是男性的概率接近于零。
在实践中,我们可以直接使用概率。因为这是分类,我们想要一个清晰的答案,我们可以将概率调整为二元类别值,例如
如果 p(男性) < 0.5,则为 0
如果 p(男性) >= 0.5,则为 1
现在我们知道了如何使用逻辑回归进行预测,让我们看看如何准备数据以充分利用该技术。
准备逻辑回归的数据
逻辑回归对您的数据分布和关系的假设与线性回归的假设几乎相同。
已经进行了大量的研究来定义这些假设,并使用了精确的概率和统计语言。我的建议是使用这些作为指导方针或经验法则,并尝试不同的数据准备方案。
最终,在预测建模机器学习项目中,您将专注于做出准确的预测,而不是解释结果。因此,只要模型稳健且表现良好,您就可以打破一些假设。
- 二元输出变量:这可能很明显,因为我们已经提到了,但逻辑回归是用于二元(两类)分类问题的。它将预测实例属于默认类别的概率,该概率可以调整为 0 或 1 的分类。
- 消除噪声:逻辑回归假设输出变量(y)没有错误,请考虑从训练数据中删除异常值和可能错误分类的实例。
- 高斯分布:逻辑回归是一种线性算法(输出有非线性变换)。它确实假设输入变量与输出之间存在线性关系。对输入变量进行更好地揭示这种线性关系的数据转换可以产生更准确的模型。例如,您可以使用 log、root、Box-Cox 和其他单变量转换来更好地揭示这种关系。
- 消除相关输入:与线性回归一样,如果您有多个高度相关的输入,模型可能会过拟合。考虑计算所有输入之间的成对相关性,并删除高度相关的输入。
- 未能收敛:学习系数的期望似然估计过程可能无法收敛。如果您的数据中有许多高度相关的输入,或者数据非常稀疏(例如,您的输入数据中有很多零),则可能会发生这种情况。
算法的主要问题
倾斜的类别分布会严重影响逻辑回归的性能,特别是在类别表示不平衡的情况下。当一个类别的实例数量远超另一个类别时,逻辑回归倾向于偏向多数类别。因此,它会失去识别和预测少数类别事件的能力,导致准确率、精确率和召回率降低,特别是影响到目标少数类别。试想一个医疗诊断场景,逻辑回归被用于预测一种罕见的疾病,其检出率仅为 3%。即使算法将所有患者预测为正常,它也达到了看似很高的 97% 的准确率,但未能实现其真实目的。
此外,对抗性攻击会通过引入细微的输入数据更改来破坏逻辑回归的性能。这些更改可能导致错误的预测,降低模型准确率。逻辑回归对微小输入扰动的敏感性使其容易受到此类攻击,从而损害了可靠性,尤其是在安全敏感的应用中。试想一个垃圾邮件分类的例子,您在底层使用了逻辑回归算法。逻辑回归就像一个电子邮件过滤器,容易受到狡猾的垃圾邮件发送者在其消息中所做的细微操纵的影响。这些微小的更改会让过滤器感到困惑,导致它错误地将垃圾邮件分类为合法电子邮件,反之亦然。因此,逻辑回归在电子邮件过滤中的可靠性受到了损害,这强调了对这类威胁进行高级防御和反措施的必要性。
算法的最新方法(2023)
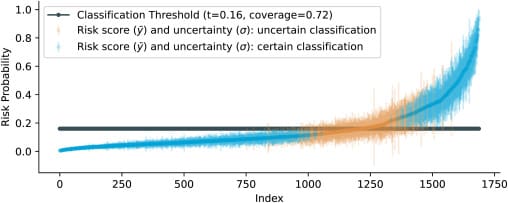
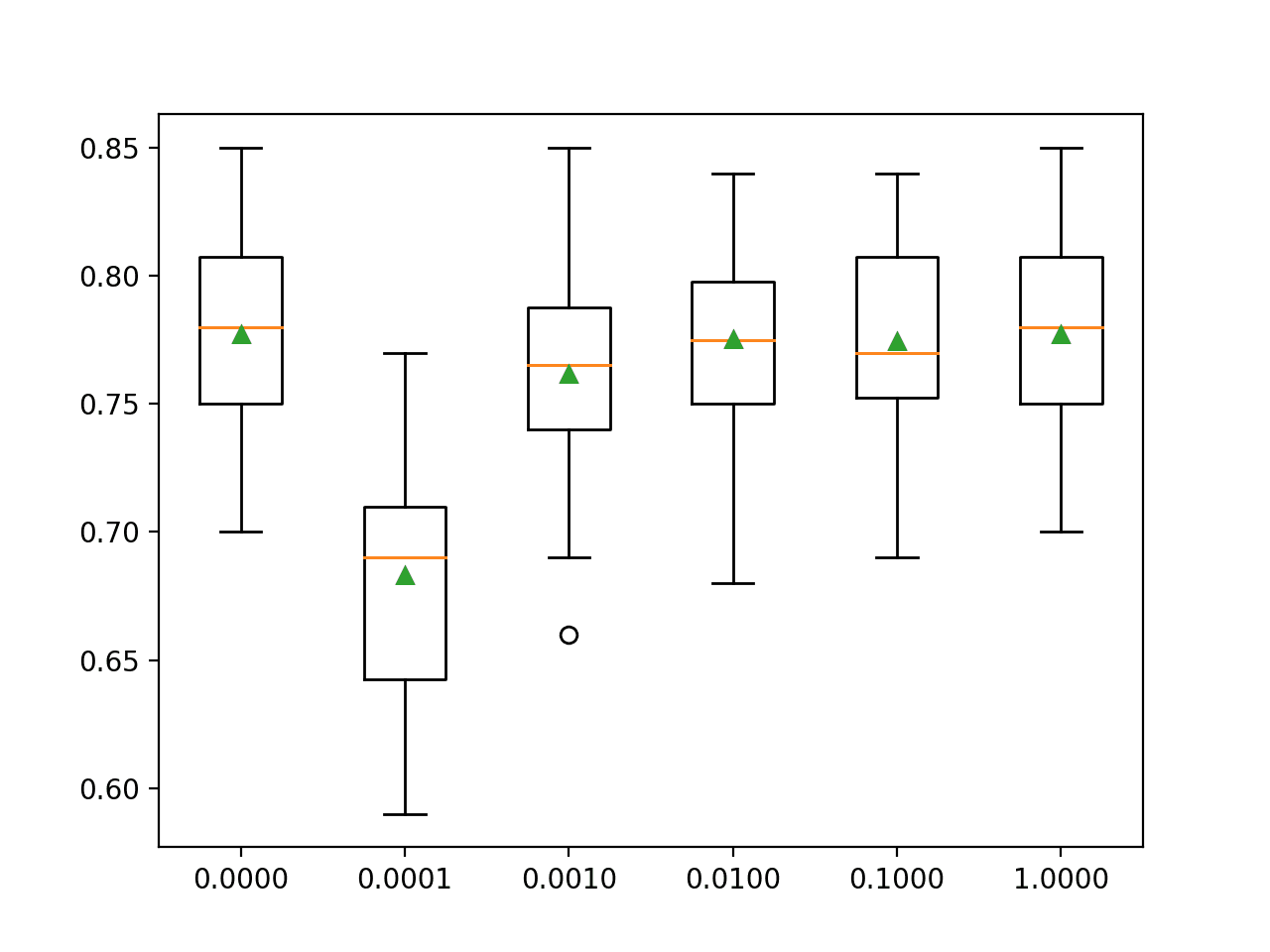
此外,论文“A Bayesian approach to predictive uncertainty”(2023)介绍了一种用于逻辑回归的贝叶斯方法,允许准确分类以及对每次预测进行可量化的不确定性估计。该研究使用来自 8000 多名癌症患者的真实电子健康记录(EHR)数据,应用贝叶斯逻辑 LASSO 回归(BLLR)来预测开始化疗的癌症患者的急性护理利用(ACU)风险。贝叶斯逻辑 LASSO 回归(BLLR)模型优于标准的逻辑 LASSO 回归,提供更高的预测准确性、良好的校准估计和更具信息量的不确定性评估。
上图显示了排序的最终风险预测(预测分布的均值,y¯)以及不确定性范围(标准差,±σ)。那些不确定性不超过决策阈值(确定分类)的预测显示为蓝色,那些超过阈值(不确定分类)的预测显示为橙色。深灰色线是研究人员选择的分类阈值,为 0.16,即事件发生率。通过贝叶斯模型确定的分类预测的比例(覆盖率)为0.72。
知名框架的逻辑回归更新
在专门的库中观察到了显著的更新,其中大多数都专注于提高算法的效率。
- TensorFlow 2.0: TensorFlow 2.0 及更高版本引入了即时执行模式,这简化了逻辑回归模型的开发和调试。
- Scikit-learn: Scikit-learn 现在提供了对处理多类别问题的改进支持,使逻辑回归在解决复杂的分类任务方面更加通用。
- Statsmodels: Statsmodels 是另一个流行的库,它增强了其统计分析和假设检验的功能,这对于基于逻辑回归的推断建模非常有用。
- InterpretML: 像 InterpretML 这样的库现在使我们能够更深入地了解和解释逻辑回归模型的结果,从而进一步增强其效用和可解释性。
机器学习框架,如 PyTorch Lightning 和 TensorFlow Serving,为训练和部署逻辑回归模型提供了简化的解决方案,优化了效率和可扩展性。
逻辑回归:在可解释人工智能和低资源/联邦环境中的多功能性
逻辑回归的适应性延伸到新兴的可解释人工智能(XAI)领域,在 XAI 中,可解释的模型对于理解和证明人工智能驱动的决策至关重要。逻辑回归的简单性和清晰的参数解释使其成为创建透明和可解释模型的宝贵工具。它能够提供对特征重要性和模型输出的直观见解,在透明度和可信度至关重要的应用中(如医疗保健、金融和法律领域)具有高度优势。
此外,逻辑回归在低资源和联邦环境中发挥着至关重要的作用。在数据有限或分布在多个来源的情况下,逻辑回归轻计算需求和高效的训练使其成为理想选择。它在提供可靠预测的同时保持数据隐私和保留资源效率的能力,使逻辑回归成为解决低资源和联邦学习环境中挑战的基础技术。
进一步阅读
关于逻辑回归的资料很多。它是许多学科(如生命科学和经济学)中的热门选择。
逻辑回归资源
查看下面的书籍以获取有关逻辑回归算法的更多详细信息。
机器学习中的逻辑回归
对于机器学习(例如,仅关注做出准确预测),请查看下面一些流行机器学习文本中对逻辑回归的介绍。
- 人工智能:现代方法,第 725-727 页
- 黑客的机器学习,第 178-182 页
- 统计学习导论:附 R 应用,第 130-137 页
- 统计学习要素:数据挖掘、推理和预测,第 119-128 页
- 应用预测建模,第 282-287 页
如果我必须选择一本,我会推荐《统计学习导论》。这本书总体上非常出色。
总结
在这篇文章中,您了解了机器学习和预测建模的逻辑回归算法。您涵盖了很多内容,并学到了
- 逻辑函数是什么以及它在逻辑回归中是如何使用的。
- 逻辑回归中的关键表示是系数,就像线性回归一样。
- 逻辑回归中的系数是通过称为最大似然估计的过程来估计的。
- 使用逻辑回归进行预测非常简单,您甚至可以在 Excel 中完成。
- 逻辑回归的数据准备与线性回归非常相似。
- 算法面临的问题和最新解决方案
- 机器学习和深度学习框架的最新更新
- 逻辑回归与 XAI
- 逻辑回归与联邦学习
您对逻辑回归或本文有任何疑问吗?
请留言提问,我将尽力回答。





如何在逻辑回归中分配权重?
它们是被学习到的,Ahmaf。
请看这篇文章
https://machinelearning.org.cn/logistic-regression-tutorial-for-machine-learning/
你能详细解释一下逻辑回归吗?如何从训练数据中学习 b0 和 b1 值?
你好 Shabir,
我在这里提供一个带有算术的教程
https://machinelearning.org.cn/logistic-regression-tutorial-for-machine-learning/
我也在这里提供一个 Python 教程
https://machinelearning.org.cn/implement-logistic-regression-stochastic-gradient-descent-scratch-python/
希望这能有所帮助。
https://desireai.com/intro-to-machine-learning/
您可以在此获得更多相关数据。
e^(b0 + b1*X) / (1 + e^(b0 + b1*X)) 怎么是逻辑函数
逻辑回归中的假设函数不是 g(transpose(theta)x) 吗,其中 g = 1/1+e^-x?
是的,您可以将方程重写为
要了解逻辑回归的实际工作原理,请参阅此教程。
https://machinelearning.org.cn/logistic-regression-tutorial-for-machine-learning/
你好 Jason,感谢您提供如此翔实的文章。
我有一个问题,我花了相当长的时间来解决。您能帮我解决吗?
假设我想做客户流失预测。现在客户流失可能发生在一年中的任何时候。我能想到的设置问题的方法有两种:
1. 设定一个参考日期,例如 16 年 11 月 1 日。依赖变量(在观测期内)通过考虑在接下来的 3 个月(11 月/12 月/1 月)内流失的客户来计算。自变量的持续时间可以固定在 15 年 11 月至 16 年 10 月(1 年),并且可以创建诸如过去 6 个月交易量之类的变量。(我认为这是更好的方法。如果我想评估模型和建立活动,这也有意义)。
2. 考虑 2016 年。对于在 16 年 7 月流失的客户(观测期),将 16 年 1 月至 6 月作为创建自变量的期间,对于在 16 年 8 月流失的客户,考虑 16 年 2 月至 7 月作为创建自变量的期间,并加上一个指标,指示客户是否在 last month 流失(自动回归,忽略案例)。按行追加此数据,然后从中随机抽取样本用于训练,其余用于测试。(我在这里感觉因变量会有季节性,因为创建的变量会考虑不同的月份)。
您能告诉我哪种方法是正确的(或者是否有任何一种是正确的)吗?这将很有帮助,因为我一直没弄明白。
此致,
Rishabh
有很多方法可以构建预测建模问题。
我建议您尝试思考问题的多种方式,在每种方式上训练和评估模型,然后深入研究最有希望的一种。
这篇文章可能会有帮助
https://machinelearning.org.cn/how-to-define-your-machine-learning-problem/
你好,
我很好奇。我看到很多网站上都有准备数据的想法,但没有多少资源能解释如何清理数据。我知道这对您来说可能非常基础,但考虑到这里有一些本科生或非 CSE 人员在阅读,您能否给我们一些指导?
数据清理是一个很难教授的主题,因为它非常特定于问题。
通常,本文档可以帮助您了解一般的数据准备过程。
https://machinelearning.org.cn/how-to-prepare-data-for-machine-learning/
本文档可以帮助您进行特征工程。
https://machinelearning.org.cn/discover-feature-engineering-how-to-engineer-features-and-how-to-get-good-at-it/
嗨 Jason 先生……我正在研究高温对人类健康的影响……例如(皮肤病)……我有两个数据集,即天气和皮肤病患者数据,在回归研究后,我发现,由于我的数据集很小,我计划使用 R 上的逻辑回归算法……你能帮忙解决这个问题吗?我将非常感谢你……
这个过程将帮助你系统地解决你的预测建模问题
https://machinelearning.org.cn/start-here/#process
你好!在学习机器学习的过程中,我一直在想,如果一个具有两个隐藏层的深度学习逻辑回归模型和普通逻辑回归模型之间有什么区别?假设有五个自变量。
它们确实非常不同。您说的“说明区别”是什么意思?苹果和橘子?
感谢您的快速回复。我实际上是在寻找公式。我知道普通逻辑回归的公式是“ln(Y) = a + b1X1 + … +bnXn”。但是,我正在寻找一个具有两个隐藏层(每个 10 个节点)的深度学习逻辑回归模型的公式。我只想知道如何用简短的公式来表示它。
你好 Dan,我建议你在描述分层模型时改用神经网络术语/拓扑结构。它不再是一个简单的线性问题。
再次感谢您的评论。那么,一个具有两个隐藏层(每个 10 个节点)和五个 X 变量以及二元目标值 Y 的深度学习模型的公式是什么?我知道我之前提到的两个模型之间的区别。我只想以数学方式表示一个深度学习模型。
通常,方程是针对前向传播或后向传播单个节点而不是整个网络来描述的。
感谢您的快速回复。我实际上是在寻找公式。我知道普通逻辑回归的公式是“ln(Y) = a + b1X1 + … +bnXn”。但是,我正在寻找一个具有两个隐藏层(每个 10 个节点)的深度学习逻辑回归模型的公式。我只想知道如何用简短的公式来表示它。
你好。请告诉我,如果数据的分布是倾斜的——右偏——我们该如何处理?
谢谢你。
可以考虑使用 box-cox 变换之类的幂变换。
先生您好,您能解释一下为什么 p=exp(b0+b1*x)/(exp(b0+b1*x)+1) 是概率吗?
你好 Jobayer,
我建议阅读一本关于该主题的教科书,例如《统计学习导论》或《统计学习要素》。
您好,布朗利先生,
谢谢您写这篇非常有信息量的文章。
我目前正在研究目标检测算法的论文,想知道如何在我的论文中确切地使用逻辑回归?
我不推荐这样做,可以考虑使用卷积神经网络。
https://machinelearning.org.cn/object-recognition-convolutional-neural-networks-keras-deep-learning-library/
面向初学者的逻辑回归简短视频教程
https://quickkt.com/tutorials/artificial-intelligence/machine-learning/logistic-regression-theory/
谢谢分享。有帮助吗?
在二元分类问题中,有没有什么好方法可以优化程序只针对 1 进行优化(而不是针对 1 和 0 进行最佳预测)——我想做的是尽可能准确地预测 1 何时发生。(我根本不在乎 0,如果我错过了一个 1,那也没关系,但是当它预测为 1 时,我希望它非常确信——所以我正在尝试看看是否有好方法只解决 1(而不是 1 和 0)?谢谢。
是的,在文献中我们称之为异常检测。
这篇文章是最好的!简洁而清晰!
谢谢您,先生!
谢谢,很高兴它有帮助。
很棒的文章。我一直在尝试阅读一本书,尽管我做了一个使用 LR 的项目,但它仍然变得很复杂。感谢您以如此简单的语言涵盖了这一点。
很高兴它有帮助。
不错的文章……易于理解……谢谢!
谢谢。
非常感谢您的文章!!!!!!!! 很有帮助!!!
不客气,很高兴听到这个消息。
嗨,Jason,
非常感谢您的文章和整个博客。在我深入学习机器学习的过程中,这些内容都非常有帮助。
我的问题与主题相关,但方向略有不同……
我已经训练并测试了一个逻辑回归模型。我信任它作为预测器,但现在我有一组人需要应用它。假设这是一个由十个人组成的群体,对于他们每个人,我都运行了一个逻辑回归模型,该模型输出了他们购买一包口香糖的概率。所以现在我有十个概率输出 [0.83, 0.71, 0.63, 0.23, 0.25, 0.41, 0.53, 0.95, 0.12, 0.66]。(从现在开始,我对每个连续的句子都有些不确定)。我可以将它们相加,然后看到最可能的结果是我将卖出 5.32 包口香糖。但是我也想知道我卖出 6 包或 5 包、4 包、9 包的概率。我想绘制某种概率分布,以显示我预计会卖给这整个群体的口香糖包数量。我有一个误差度量,所以我可以计算标准差,然后绘制某种正态分布,以 5.32 为中心,来显示不同结果的概率,对吧?
我认为这一切都有道理,但随后会变得有些复杂。我有其他人,具有不同的特征和不同的分类器。我正在测试相同的结果(他们会买一包口香糖),但这些人可能已经在我的店里了。我有五个人,他们的概率是 [0.93, 0.85, 0.75, 0.65, 0.97]。所以,我预计最可能的结果是,我将向这五个人总共卖出 4.15 包口香糖。太好了,但现在我有两个不同的分类器,处理两个不同的人群,并有两个不同的误差度量。我假设最可能的结果是我总共卖出 9.47 包口香糖(第一组 5.32 包,第二组 4.15 包)。但是,我如何确定我在这两个群体之间总共卖出 10 包的可能性?12 包?5 包?当我有了两个不同的分类器处理两个不同的人群时,我该如何得到一个正态分布?
这真是个庞大的评论。快速浏览一下您的评论,我觉得您对预测区间感兴趣。
https://en.wikipedia.org/wiki/Prediction_interval
这正确吗?
嘿 Jason,您的教程对像我这样的初学者来说太棒了,感谢您系统且轻松地进行解释。
谢谢,很高兴它们有帮助。
您能告诉我逻辑回归的处理速度是多少吗?它与其他预测建模类型(如随机森林或 One-R)相比如何?
谢谢!
也许您可以编写代码来比较执行时间?
嗨,Jason,
我有一个关于您在此处示例的问题,其中根据身高预测性别。
使用 Logit 函数,我们得出结论 p(男性 | 身高 = 150cm) 接近 0。利用这些信息,当我得知输出被归类为男性或女性时,我能说出 p(女性 | 身高 = 150cm) 的情况吗?
一如既往,内容丰富且清晰😉
谢谢。
非常感谢,这消除了我的许多疑虑。
很高兴听到这个消息。
感谢您的文章和其他文章!它们对我这样的初学者非常有帮助。
谢谢,很高兴听到这个。
谢谢,对我很有帮助。
我很高兴听到它有帮助。
Jason,你太棒了!你总是能用通俗易懂的方式解释复杂的方法!
谢谢!
谢谢。我很高兴它有帮助。
感谢这篇信息丰富的文章。我有一个关于确定逻辑回归响应(主要事件的概率)的输入变量值的问题。
假设自变量是指治疗方案,因变量是指不重新入院医院。目标是确定最有效的治疗方案,更可能是治疗方案的组合,以最大化不重新入院的概率。
您建议我如何确定哪些选项或组合最有效?
我应该遵循:1)构建逻辑回归模型 2)确定系数后,假设最大化概率,然后确定自变量的值?找到优化响应变量的输入值的更好方法是什么?
谢谢你。
好问题,也许可以将其视为一个优化问题,并使用拟合的模型来寻找最大化输出的值。
请问您是如何得到 b0 为 -100 且 b1 为 0.6 的?
我任意设置的。
您可以使用优化过程找到逻辑回归的系数,例如二次优化或梯度下降。
https://machinelearning.org.cn/implement-logistic-regression-stochastic-gradient-descent-scratch-python/
嗨,Jason,
非常感谢您以如此易懂的方式分享您的知识!这对我很有帮助。但是,我仍然在努力解决一个(也许是相当具体?)的问题。
在我研究的案例中,成功概率预计不会达到 100%。事实上,实际概率范围在 0 到 a% 之间。而 a 是未知的。
我相信在我的情况下,我将需要类似 P(X) = a / (1 + e^(b + c*(X)) 的东西。
但是,应用 logit 和 ML 方法会出现问题。
您是否知道如何解决这个问题?什么方法会比较好?
或者逻辑回归可能不是解决这个问题的最佳选择?朴素贝叶斯是否会是更好的选择?
非常感谢!
此致,Maarten
很好的问题!
我建议您在 math overflow 上重新发布此问题,并从真正懂数学的人那里得到答案,我预计有一种方法可以正确地约束模型以满足您的需求,而且我不想虚构内容来误导您。
嗨,Jason,
谢谢您提供的信息。我有一个问题,我还不完全理解。我看到一些专家和老师说,逻辑回归对自变量的分布没有假设,它们不必是正态分布、线性相关或各组方差相等。这与您对逻辑回归的解释如何吻合?希望您能帮助我理解。谢谢
这里有一个链接提到了这一点
http://userwww.sfsu.edu/efc/classes/biol710/logistic/logisticreg.htm
Jason Brownlee 2019年2月21日 下午2:04 #
也许和材料的作者/所有者谈谈?
我问了他们,正在等待他们的回复。
但与此同时,这里还有另一个链接。
https://www.quora.com/Does-logistic-regression-require-independent-variables-to-be-normal-distributed
有人问了这个问题,一些专家回答说逻辑回归不假设您的自变量是正态分布的。
有趣,谢谢。
根据他们的回答,我发现:逻辑回归或线性回归算法确实假设您的自变量和因变量之间存在线性关系,但它们不对自变量具有任何特定分布做假设。只是如果我将连续自变量的分布转换为正态分布形式,它会更好地揭示这种线性关系。
您怎么看?对吗?
与我的理解不符——至少在关于线性回归方面。逻辑回归没有分布,目标是二元的。
嗨 Jason,引用的书籍《统计学习要素:数据挖掘、推理和预测》的页码应该是 119-128 吗?
是的,谢谢。已修正。
嗨,Jason,
感谢您对逻辑回归的详细解释/教程。
我有一些关于逻辑回归的查询,我在互联网或书籍中找不到答案。如果您能帮助我理解这些未解的疑问,将非常有帮助。
1. Logit 函数(即 Logit 方程 LN(P/1-P))是从逻辑回归方程推导出来的,还是反之?
2. Logit 方程在逻辑回归方程中的目的是什么?Logit 函数如何在逻辑回归算法中使用?提出这个问题的理由将在看完第 3 和第 4 点后变得清楚。
3. 在构建逻辑回归模型后,我们得到模型系数。当我们把这些模型系数和相应的预测值代入
逻辑回归方程,我们得到默认类别的概率值(与 predict() 返回的值相同)。这是否意味着估计的模型系数是基于概率值(使用逻辑回归方程而不是 logit 方程计算)确定的,这些概率值将输入到似然函数中以确定它是否最大化了它?如果这个理解是正确的,那么在整个模型构建过程中,logit 函数在哪里被使用?
4. 在模型构建或预测值时都不使用 logit 函数。如果情况是这样,为什么我们重视 logit 函数,它用于将概率值映射到实数值(范围从 -Inf 到 +Inf)?在整个逻辑回归模型构建过程中,logit 函数究竟在哪里使用?是在估计模型系数时吗?
5. 我们在运行 summary(lr_model) 时看到的模型系数估计是使用逻辑回归方程(logit 方程)的线性形式还是实际的逻辑回归方程确定的?
抱歉,我不会在此博客中介绍方程的推导。
也许可以尝试在 mathoverflow 上发布您的问题?
Log odds 就是 logit 而不是 probit,对吗?
Log odds 就是 logit。
大家好,
我有一个问题,我将数据分为 80% 训练集和 20% 测试集。然后我应用了梯度提升,但是测试得分结果是 1.0。这让我觉得有些奇怪。我该如何解释这个结果?
谢谢你。
也许问题太简单/平凡了?
如果是这样,我应该依赖这个结果吗?即使它非常简单?我的意思是,如果我相信我正确地识别了问题,即使我得到了过高的测试结果,我也应该相信这个结果吗?
如果不是,那么如何解决这个问题太简单化的问题?增加列和观测的数量?还是其他什么?
谢谢,伙计。
您的目标是设计一个允许结果被信任的测试框架。
这意味着要确保训练数据集可靠,并使用 k 折交叉验证等技术。
https://machinelearning.org.cn/k-fold-cross-validation/
嗨,Jason,
我尝试了 k 折交叉验证,测试准确率仍然在 98% 左右。那么,我现在可以信任这些结果并使用这个模型吗?
(顺便说一下;
观测数:3000,
特征数:1131,
PCA 使用的 n 个分量 = 20
)
根据以上信息,逻辑回归的结果是训练准确率=99%,测试准确率=98.3%。
谢谢你。
我相信是的。
已更新**
(顺便说一下;
观测数:3000,
特征数:1131,
交叉验证*:20
)
我还有一个问题:我的目标列(y)类型是 object,它包含值“A”、“B”和“C”。我应该将其从 object 转换为 Categorical,如下所示吗?
y = pd.Categorical(y)
还是应该将其保留为 object。
谢谢你。
在建模之前对类别变量进行独热编码是一个好主意。更多信息请看这里。
https://machinelearning.org.cn/why-one-hot-encode-data-in-machine-learning/
谢谢你
嗨,Jason,
谢谢您的帖子!我正在尝试解决二元图像分类(例如,马或狗)。由于图像尺寸(100 x 100)很大,我是否可以先使用 PCA 来降低维度,还是 LG 可以处理?高度相关的特征或多重共线性怎么办?您推荐哪种方式?
谢谢您的回复。
也许可以尝试在原始像素数据上使用一系列模型。
您会发现 CNN 模型在这方面通常会胜过其他模型。
嗨
我正在尝试对 fashion_mnist 进行量化。
但我不知道正确的量化模型方法。
您能帮帮我吗?
您为什么要进行量化?
有一些 theta 和矩阵参数是 FP32,我需要将其减至 FP8。
我完全不明白。FP32 和 FP8 是什么?
浮点数 32 和 8。
以下是该示例的链接。
https://nbviewer.jupyter.org/github/trekhleb/homemade-machine-learning/blob/master/notebooks/logistic_regression/multivariate_logistic_regression_fashion_demo.ipynb
在我的分类问题中,说逻辑回归是线性模型是否正确?
是的。
谢谢
不客气。
你好,您提到“逻辑回归模型化了默认类(例如,第一个类别)的概率”。我无法理解“默认/第一个类别”是什么意思,或者这如何定义。您能帮我理解一下吗?
是的,它回到了二项概率分布。
https://machinelearning.org.cn/discrete-probability-distributions-for-machine-learning/
我想我提交得太快了!在我先前的评论中,我的意思是如果存在两个类别,如何确定哪个被视为默认类别或第一个类别。
请参阅这里的伯努利/二项分布。
https://machinelearning.org.cn/discrete-probability-distributions-for-machine-learning/
您能提供任何推导吗?我在任何地方都找不到。
ln(p(X) / 1 – p(X)) = b0 + b1 * X
是的,请参阅教程的“进一步阅读”部分。
我开始了一个 udemy 课程,学习使用 AzureML 的机器学习,讲师解释了逻辑回归,但我没能理解。我想进一步探索它,然后我访问了维基百科,但我遇到了更多新词,比如‘odd’等等,我又不能继续读下去了……
然后我来到了这里……我非常赞赏您让机器学习概念易于理解的努力!它让我对这门课程更加充满热情……
非常感谢..
谢谢,坚持下去!
你好 Jason,感谢您撰写这篇内容丰富的帖子。
我有一个关于逻辑回归在二元分类中“默认类别”的问题。逻辑回归实际上是如何决定将哪个类别作为计算几率的参考的?
在这篇文章的开头,您提到默认类别可以是“第一类”,这是否意味着训练数据集中第一行出现的第一个类别?
这里还有您的另一篇帖子:https://machinelearning.org.cn/logistic-regression-tutorial-for-machine-learning/
其中提到默认类别是类别 0!
那么,本质上,Log.Regression 模型将哪个类别作为默认类别或基线?您能帮我理解一下吗?
类别 1 (class=1) 是默认类别,例如,我们正在预测输入属于类别 1 的概率。
Jason Brownlee 先生,感谢您分享有关逻辑回归的信息。这对我很有帮助。
您的教程非常棒。关于这个主题,我尝试在没有 sklearn 的情况下使用 L2 正则化来实现 SDG,我的代码不断抛出“index to scalar variable”的错误。如果您可以帮助我,我可以给您发送代码片段吗?谢谢。
也许可以尝试将您的代码和错误发布到 stackoverflow.com。
非常有用的文章,谢谢分享。
谢谢!
这非常有帮助。
谢谢!
非常有用的文章,谢谢分享。
谢谢。
谢谢你
不客气!
不客气!
非常有用的文章,谢谢分享。
谢谢!
逻辑回归这个主题非常好,非常感谢。
不客气。
很棒的概念,对我们很有帮助。
谢谢。
嗨,Jason,
我想知道为什么数据中的高相关性会导致逻辑回归无法收敛?
谢谢。
一般来说,如果输入数据高度相关,您就会遇到共线性问题。这会使优化结果不稳定。
嗨,Jason,
此外,还有一个关于“高度相关的特征会导致模型过拟合”的问题?根据我的阅读:https://stats.stackexchange.com/questions/250376/feature-correlation-and-their-effect-of-logistic-regression
似乎相关的特征只会带来更差的 LR 性能。请指导。谢谢。
感谢您的讲解,信息量很大。
很棒的概念,对我们很有帮助。
谢谢。很高兴你喜欢。
感谢您的讲解,信息量很大。
非常有用的文章,谢谢分享。
嗨,Jason,
关于逻辑回归的优秀文章。
我有一个问题:在初步步骤中提到
p(X) = e^(b0 + b1*X) / (1 + e^(b0 + b1*X)) [这个我理解得很清楚]。但我没理解的是
两边取 ln(自然对数)
给出的简化步骤是
ln(p(X) / 1 – p(X)) = b0 + b1 * X
我看过简化过程,但我无法推导出这个等式。您能解释一下这个等式是如何在简化后得出的吗?
Krish
你好 Krishnamohan…以下资源应该会让你更清楚。
https://www.dummies.com/article/academics-the-arts/math/pre-calculus/how-to-solve-an-exponential-equation-by-taking-the-log-of-both-sides-167857/
你好,
我能问一下,您是如何在“Making Predictions with Logistic Regression”的子标题部分得到结果的,只有那一部分?
我已阅读整篇文章,如果我在电子表格中手动进行计算并输入,它们都能正常工作,但当我只尝试为这个例子进行计算时,我无法得到相同的 y 输出。
文本中的示例显示如下:
y = e^(b0 + b1*X) / (1 + e^(b0 + b1*X))
y = exp(-100 + 0.6*150) / (1 + EXP(-100 + 0.6*150))
y = 0.0000453978687
根据建议,我正在使用 Excel 中的 EXP 函数来跟踪该示例,但我没有得到 y=0.0000453978687。对于其他示例和其他统计教科书示例,它们输入正常,这篇文章中的其他所有内容也正常,只有那个示例与我的输出不匹配,我想了解原因,以防我只是犯了一个基本错误。
我能否检查一下,当将这个虚构示例输入 Excel 或手动进行计算时,您或其他人是否得到了这个值 – 0.0000453978687?exp(-100 + 0.6*150) / (1 + EXP(-100 + 0.6*150))
顺便说一句,这是一篇很棒的文章。
提前感谢您的时间,
Niall
感谢您的反馈!我们将审查子标题和相关计算。希望其他人也能分享他们的结果。
我喜欢这个解释!但是,我认为以下内容令人困惑
“我们正在对输入 (X) 属于默认类别 (Y=1) 的概率进行建模,并且可以将其形式化地写为:P(X) = P(Y=1|X)”
符号 P(X) = P(Y=1|X) 意味着某个特征 X 发生的概率等于特征 X 发生的条件下类别 Y=1 发生的概率。但这不可能是正确的。也许我遗漏了什么简单的问题。
我很想知道您对 P(X) = P(Y=1|X) 的意思。
你好 Yuriy… 感谢您的反馈!