OpenCV 中的逻辑回归

作者： Stefania Cristina 于 2024年1月30日发布在 OpenCV 0

逻辑回归是一种简单但流行的用于二元分类的机器学习算法，其核心是使用逻辑函数或称为 Sigmoid 函数。OpenCV 库也实现了该算法。

在本教程中，您将学习如何应用 OpenCV 的逻辑回归算法，首先从我们将自己生成的一个自定义二分类数据集开始。然后，在后续教程中，我们将把这些技能应用于具体的图像分类应用。

完成本教程后，您将了解：

逻辑回归算法的几个最重要的特性。
如何在 OpenCV 中将逻辑回归算法用于自定义数据集。

通过我的书《OpenCV 机器学习》启动您的项目。它提供了带有可用代码的自学教程。

让我们开始吧。

OpenCV 中的逻辑回归
照片由 Fabio Santaniello Bruun 拍摄。部分权利保留。

教程概述

本教程分为两部分；它们是

回顾逻辑回归是什么
在 OpenCV 中发现逻辑回归

回顾逻辑回归是什么

Jason Brownlee 在这些教程中已经很好地解释了逻辑回归的主题[1, 2, 3]，但让我们先来复习一些最重要的要点。

逻辑回归的名字来源于其核心使用的函数，即逻辑函数（也称为 Sigmoid 函数）。

尽管名称中使用了“回归”一词，但逻辑回归是一种用于二元分类的方法，或者说，更简单地说是具有两个类别值的问题。

逻辑回归可以被视为线性回归的扩展，因为它通过使用逻辑函数将特征的线性组合的实值输出映射（或“压缩”）到 [0, 1] 范围内的概率值。

在二分类场景中，逻辑回归模型对默认类别的概率进行建模。举个简单的例子，假设我们试图根据花瓣数量区分 A 类和 B 类花，我们将默认类别设为 A。那么，对于一个未知的输入 X，逻辑回归模型将给出 X 属于默认类别 A 的概率。

$$ P(X) = P(A = 1 | X) $$

当其概率 P(X) > 0.5 时，输入 X 被分类为属于默认类别 A。否则，它被分类为属于非默认类别 B。

逻辑回归模型由一组称为系数（或权重）的参数表示，这些参数从训练数据中学习。在训练过程中，这些系数会通过迭代进行调整，以最小化模型预测与实际类别标签之间的误差。

系数的值可以在训练过程中使用梯度下降或最大似然估计（MLE）技术来估计。

在 OpenCV 中发现逻辑回归

在转向更复杂的问题之前，让我们从一个简单的二元分类任务开始。

正如我们在相关的教程中已经完成的，通过这些教程我们熟悉了 OpenCV 中的其他机器学习算法（例如 SVM 算法），我们将生成一个包含 100 个数据点（由 n_samples 指定）、平均分为 2 个高斯簇（由 centers 指定）且标准差设置为 5（由 cluster_std 指定）的数据集。为了能够重现结果，我们将再次利用 random_state 参数，将其设置为 15：

# Generate a dataset of 2D data points and their ground truth labels
x, y_true = make_blobs(n_samples=100, centers=2, cluster_std=5, random_state=15)

# Plot the dataset
scatter(x[:, 0], x[:, 1], c=y_true)
show()

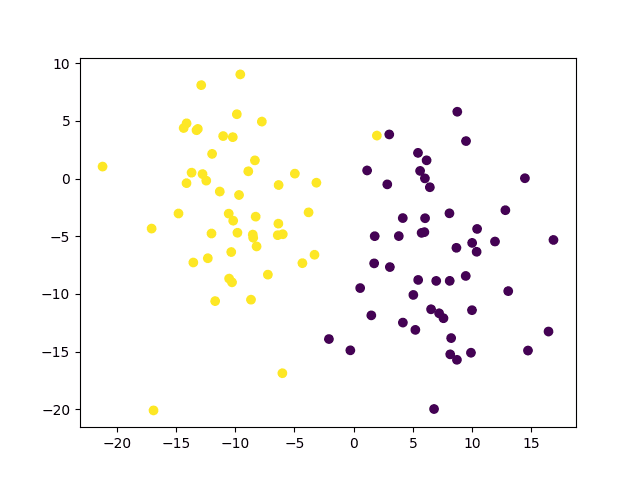
# 生成一个二维数据点及其真实标签的数据集

x, y_true = make_blobs(n_samples=100, centers=2, cluster_std=5, random_state=15)

# 绘制数据集

scatter(x[:, 0], x[:, 1], c=y_true)

show()

上面的代码应该会生成以下数据点图。您可能会注意到，我们将颜色值设置为地面真实标签，以便能够区分属于两个不同类别的数据点。

属于两个不同类别的数据点

下一步是将数据集拆分为训练集和测试集，前者将用于训练逻辑回归模型，后者将用于测试模型。

# Split the data into training and testing sets
x_train, x_test, y_train, y_test = ms.train_test_split(x, y_true, test_size=0.2, random_state=10)

# Plot the training and testing datasets
fig, (ax1, ax2) = subplots(1, 2)
ax1.scatter(x_train[:, 0], x_train[:, 1], c=y_train)
ax1.set_title('Training data')
ax2.scatter(x_test[:, 0], x_test[:, 1], c=y_test)
ax2.set_title('Testing data')
show()

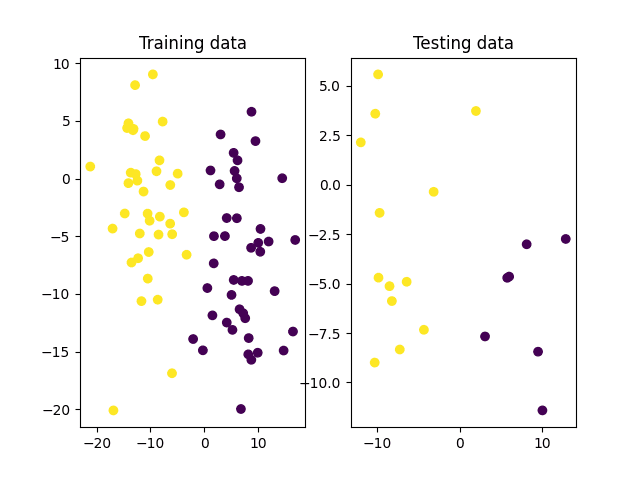
# 将数据拆分为训练集和测试集

x_train, x_test, y_train, y_test = ms.train_test_split(x, y_true, test_size=0.2, random_state=10)

# 绘制训练集和测试集

fig, (ax1, ax2) = subplots(1, 2)

ax1.scatter(x_train[:, 0], x_train[:, 1], c=y_train)

ax1.set_title('Training data')

ax2.scatter(x_test[:, 0], x_test[:, 1], c=y_test)

ax2.set_title('Testing data')

show()

将数据点拆分为训练集和测试集

上图表明，在训练集和测试集中，两个类别明显可分。因此，我们预计这种二元分类问题对于训练好的逻辑回归模型来说将是一项简单的任务。让我们在 OpenCV 中创建一个逻辑回归模型并进行训练，以便最终了解它在测试集上的表现。

第一步是创建逻辑回归模型本身。

# Create an empty logistic regression model
lr = ml.LogisticRegression_create()

1 2	# 创建一个空的逻辑回归模型 lr = ml.LogisticRegression_create()

在下一步中，我们将选择一种训练方法，用于在训练期间更新模型的系数。OpenCV 实现允许我们在两种不同的方法之间进行选择：批量梯度下降和小批量梯度下降方法。

如果选择批量梯度下降方法，则模型系数将在梯度下降算法的每次迭代中使用整个训练数据集进行更新。如果我们处理的是非常大的数据集，那么这种更新模型系数的方法可能会变得计算成本非常高。

想开始学习 OpenCV 机器学习吗？

立即参加我的免费电子邮件速成课程（附示例代码）。

点击注册，同时获得该课程的免费PDF电子书版本。

更新模型系数的一种更实用的方法，尤其是在处理大型数据集时，是选择小批量梯度下降方法，该方法将训练数据分成更小的批次（称为小批量，因此得名），并一次处理一个批次来更新模型系数。

我们可以使用以下代码行来检查 OpenCV 的默认训练方法。

# Check the default training method
print(‘Training Method:’, lr.getTrainMethod())

1 2	# 检查默认训练方法 print(‘Training Method:’, lr.getTrainMethod())

Training Method: 0

训练方法：0

返回的 0 代表 OpenCV 中的批量梯度下降方法。如果我们想将其更改为小批量梯度下降方法，可以通过将 ml.LogisticRegression_MINI_BATCH 传递给 setTrainMethod 函数来实现，然后继续设置小批量的大小。

# Set the training method to Mini-Batch Gradient Descent and the size of the mini-batch
lr.setTrainMethod(ml.LogisticRegression_MINI_BATCH)
lr.setMiniBatchSize(5)

# 将训练方法设置为小批量梯度下降并设置小批量的大小

lr.setTrainMethod(ml.LogisticRegression_MINI_BATCH)

lr.setMiniBatchSize(5)

将小批量大小设置为 5 意味着训练数据将被分成包含 5 个数据点的小批量，并且在依次处理完每个小批量后，模型的系数会进行迭代更新。如果我们把小批量的大小设置为训练数据集的总样本数，那么这实际上将等同于批量梯度下降操作，因为在每次迭代中都会一次性处理整个训练数据批次。

接下来，我们将定义希望运行所选训练算法的迭代次数，然后才能终止。

# Set the number of iterations
lr.setIterations(10)

1 2	# 设置迭代次数 lr.setIterations(10)

现在我们准备好在训练数据上训练逻辑回归模型了。

# Train the logistic regressor on the set of training data
lr.train(x_train.astype(float32), ml.ROW_SAMPLE, y_train.astype(float32))

1 2	# 在训练数据集上训练逻辑回归器 lr.train(x_train.astype(float32), ml.ROW_SAMPLE, y_train.astype(float32))

如前所述，训练过程旨在通过迭代调整逻辑回归模型的系数来最小化模型预测与实际类别标签之间的误差。

我们输入到模型中的每个训练样本都包含两个特征值，分别用 $x_1$ 和 $x_2$ 表示。这意味着我们应该期望生成的模型由两个系数（每个输入特征一个）和一个定义偏差（或截距）的附加系数来定义。

那么模型返回的概率值 $\hat{y}$ 可以定义为：

$$ \hat{y} = \sigma( \beta_0 + \beta_1 \; x_1 + \beta_2 \; x_2 ) $$

其中 $\beta_1$ 和 $\beta_2$ 表示模型系数，$\beta_0$ 表示偏差，$\sigma$ 表示应用于特征线性组合的实值输出的逻辑（或 Sigmoid）函数。

让我们打印出学习到的系数，看看是否得到了预期的数量。

# Print the learned coefficients
print(lr.get_learnt_thetas())

1 2	# 打印学习到的系数 print(lr.get_learnt_thetas())

[[-0.02413555 -0.34612912  0.08475047]]

1	[[-0.02413555 -0.34612912 0.08475047]]

我们发现得到了三个值，正如预期的那样，这意味着我们可以通过以下方式定义最能分离我们正在处理的两个类别样本的模型：

$$ \hat{y} = \sigma( -0.0241 – \; 0.3461 \; x_1 + 0.0848 \; x_2 ) $$

通过将新的、未见过的数据点的特征值 $x_1$ 和 $x_2$ 代入上述模型，我们可以将该数据点分配给两个类别中的任何一个。如果模型返回的概率值大于 0.5，我们可以将其视为类别 0（默认类别）的预测。否则，它是类别 1 的预测。

让我们通过在测试集上进行尝试，来看看这个模型对目标类别的预测效果如何。

# Predict the target labels of the testing data
_, y_pred = lr.predict(x_test.astype(float32))

# Compute and print the achieved accuracy
accuracy = (sum(y_pred[:, 0].astype(int) == y_test) / y_test.size) * 100
print('Accuracy:', accuracy, ‘%')

# 预测测试数据的目标标签

_, y_pred = lr.predict(x_test.astype(float32))

# 计算并打印获得的准确度

accuracy = (sum(y_pred[:, 0].astype(int) == y_test) / y_test.size) * 100

print('Accuracy:', accuracy, ‘%')

Accuracy: 95.0 %

1	准确率：95.0 %

我们可以绘制测试数据的真实值与预测类别，并打印出真实值和预测类别标签，以调查任何误分类。

# Plot the ground truth and predicted class labels
fig, (ax1, ax2) = subplots(1, 2)
ax1.scatter(x_test[:, 0], x_test[:, 1], c=y_test)
ax1.set_title('Ground Truth Testing data')
ax2.scatter(x_test[:, 0], x_test[:, 1], c=y_pred)
ax2.set_title('Predicted Testing data’)
show()

# Print the ground truth and predicted class labels of the testing data
print('Ground truth class labels:', y_test, '\n',
      'Predicted class labels:', y_pred[:, 0].astype(int))

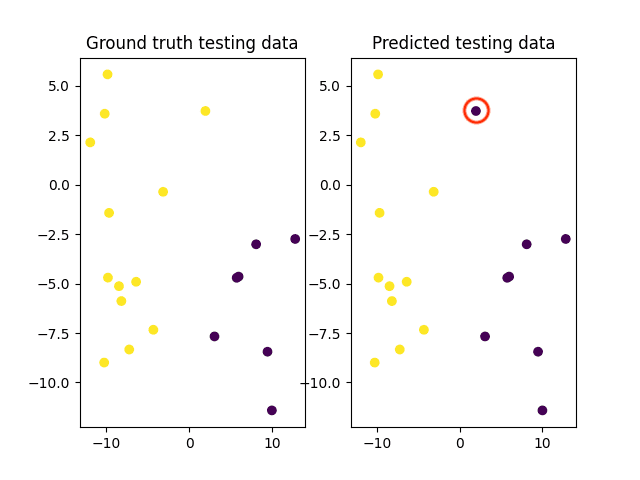
# 绘制真实值和预测类别标签

fig, (ax1, ax2) = subplots(1, 2)

ax1.scatter(x_test[:, 0], x_test[:, 1], c=y_test)

ax1.set_title('Ground Truth Testing data')

ax2.scatter(x_test[:, 0], x_test[:, 1], c=y_pred)

ax2.set_title('Predicted Testing data’)

show()

# 打印测试数据的真实值和预测类别标签

print('Ground truth class labels:', y_test, '\n',

'Predicted class labels:', y_pred[:, 0].astype(int))

Ground truth class labels: [1 1 1 1 1 0 0 1 1 1 0 0 1 0 0 1 1 1 1 0] 
Predicted class labels: [1 1 1 1 1 0 0 1 0 1 0 0 1 0 0 1 1 1 1 0]

1 2	真实类别标签：[1 1 1 1 1 0 0 1 1 1 0 0 1 0 0 1 1 1 1 0] 预测类别标签：[1 1 1 1 1 0 0 1 0 1 0 0 1 0 0 1 1 1 1 0]

测试数据点属于真实值和预测类别，其中红圈突出显示了一个误分类的数据点

这样，我们就可以看到，在一个样本中，真实数据中它属于类别 1，但在模型的预测中被错误地归类为类别 0。

完整的代码列表如下：

from cv2 import ml
from sklearn.datasets import make_blobs
from sklearn import model_selection as ms
from numpy import float32
from matplotlib.pyplot import scatter, show, subplots

# Generate a dataset of 2D data points and their ground truth labels
x, y_true = make_blobs(n_samples=100, centers=2, cluster_std=5, random_state=15)

# Plot the dataset
scatter(x[:, 0], x[:, 1], c=y_true)
show()

# Split the data into training and testing sets
x_train, x_test, y_train, y_test = ms.train_test_split(x, y_true, test_size=0.2, random_state=10)

# Plot the training and testing datasets
fig, (ax1, ax2) = subplots(1, 2)
ax1.scatter(x_train[:, 0], x_train[:, 1], c=y_train)
ax1.set_title('Training data')
ax2.scatter(x_test[:, 0], x_test[:, 1], c=y_test)
ax2.set_title('Testing data')
show()

# Create an empty logistic regression model
lr = ml.LogisticRegression_create()

# Check the default training method
print('Training Method:', lr.getTrainMethod())

# Set the training method to Mini-Batch Gradient Descent and the size of the mini-batch
lr.setTrainMethod(ml.LogisticRegression_MINI_BATCH)
lr.setMiniBatchSize(5)

# Set the number of iterations
lr.setIterations(10)

# Train the logistic regressor on the set of training data
lr.train(x_train.astype(float32), ml.ROW_SAMPLE, y_train.astype(float32))

# Print the learned coefficients
print(lr.get_learnt_thetas())

# Predict the target labels of the testing data
_, y_pred = lr.predict(x_test.astype(float32))

# Compute and print the achieved accuracy
accuracy = (sum(y_pred[:, 0].astype(int) == y_test) / y_test.size) * 100
print('Accuracy:', accuracy, '%')

# Plot the ground truth and predicted class labels
fig, (ax1, ax2) = subplots(1, 2)
ax1.scatter(x_test[:, 0], x_test[:, 1], c=y_test)
ax1.set_title('Ground truth testing data')
ax2.scatter(x_test[:, 0], x_test[:, 1], c=y_pred)
ax2.set_title('Predicted testing data')
show()

# Print the ground truth and predicted class labels of the testing data
print('Ground truth class labels:', y_test, '\n',
      'Predicted class labels:', y_pred[:, 0].astype(int))

from cv2 import ml

from sklearn.datasets import make_blobs

from sklearn import model_selection as ms

from numpy import float32

from matplotlib.pyplot import scatter, show, subplots

# 生成一个二维数据点及其真实标签的数据集

x, y_true = make_blobs(n_samples=100, centers=2, cluster_std=5, random_state=15)

# 绘制数据集

scatter(x[:, 0], x[:, 1], c=y_true)

show()

# 将数据拆分为训练集和测试集

x_train, x_test, y_train, y_test = ms.train_test_split(x, y_true, test_size=0.2, random_state=10)

# 绘制训练集和测试集

fig, (ax1, ax2) = subplots(1, 2)

ax1.scatter(x_train[:, 0], x_train[:, 1], c=y_train)

ax1.set_title('Training data')

ax2.scatter(x_test[:, 0], x_test[:, 1], c=y_test)

ax2.set_title('Testing data')

show()

# 创建一个空的逻辑回归模型

lr = ml.LogisticRegression_create()

# 检查默认训练方法

print('Training Method:', lr.getTrainMethod())

# 将训练方法设置为小批量梯度下降并设置小批量的大小

lr.setTrainMethod(ml.LogisticRegression_MINI_BATCH)

lr.setMiniBatchSize(5)

# 设置迭代次数

lr.setIterations(10)

# 在训练数据集上训练逻辑回归器

lr.train(x_train.astype(float32), ml.ROW_SAMPLE, y_train.astype(float32))

# 打印学习到的系数

print(lr.get_learnt_thetas())

# 预测测试数据的目标标签

_, y_pred = lr.predict(x_test.astype(float32))

# 计算并打印获得的准确度

accuracy = (sum(y_pred[:, 0].astype(int) == y_test) / y_test.size) * 100

print('Accuracy:', accuracy, '%')

# 绘制真实值和预测类别标签

fig, (ax1, ax2) = subplots(1, 2)

ax1.scatter(x_test[:, 0], x_test[:, 1], c=y_test)

ax1.set_title('Ground truth testing data')

ax2.scatter(x_test[:, 0], x_test[:, 1], c=y_pred)

ax2.set_title('Predicted testing data')

show()

# 打印测试数据的真实值和预测类别标签

print('Ground truth class labels:', y_test, '\n',

'Predicted class labels:', y_pred[:, 0].astype(int))

在本教程中，我们考虑了 OpenCV 中实现的逻辑回归模型的两个特定训练参数的设置。这些参数定义了要使用的训练方法以及在训练过程中希望运行所选训练算法的迭代次数。

但是，这些并不是逻辑回归方法可以设置的唯一参数值。诸如学习率和正则化类型等其他参数也可以进行修改以获得更好的训练准确率。因此，我们建议您探索这些参数，并研究不同的值如何影响模型的训练和预测准确率。

进一步阅读

如果您想深入了解此主题，本节提供了更多资源。

书籍

OpenCV 机器学习, 2017.
使用 Python 精通 OpenCV 4, 2019.

网站

逻辑回归，https://docs.opencv.ac.cn/3.4/dc/dd6/ml_intro.html#ml_intro_lr

总结

在本教程中，您学习了如何应用 OpenCV 的逻辑回归算法，从我们生成的一个自定义二分类数据集开始。

具体来说，你学到了：

逻辑回归算法的几个最重要的特性。
如何在 OpenCV 中将逻辑回归算法用于自定义数据集。

你有什么问题吗？

在下面的评论中提出您的问题，我将尽力回答。

开始使用 OpenCV 进行机器学习！

学习如何在图像处理项目中使用机器学习技术

...以高级方式使用 OpenCV，超越像素处理

在我的新电子书中探索如何实现
OpenCV 机器学习

它提供带有所有可用 Python 代码的自学教程，让您从新手成长为专家。它为您提供了
逻辑回归、随机森林、支持向量机、k 均值聚类、神经网络等等……所有这些都使用 OpenCV 中的机器学习模块

通过动手练习开启你的深度学习之旅

查看内容

关于此主题的更多信息

分类, 逻辑回归, OpenCV, 回归

导航

OpenCV 中的逻辑回归

教程概述

回顾逻辑回归是什么

在 OpenCV 中发现逻辑回归

想开始学习 OpenCV 机器学习吗？

进一步阅读

书籍

网站

总结

开始使用 OpenCV 进行机器学习！

学习如何在图像处理项目中使用机器学习技术

通过动手练习开启你的深度学习之旅

关于此主题的更多信息

暂无评论。

发表回复点击此处取消回复。

导航

教程概述

回顾逻辑回归是什么

在 OpenCV 中发现逻辑回归

想开始学习 OpenCV 机器学习吗？

进一步阅读

书籍

网站

总结

开始使用 OpenCV 进行机器学习！

学习如何在图像处理项目中使用机器学习技术

通过动手练习开启你的深度学习之旅

关于此主题的更多信息

暂无评论。

发表回复 点击此处取消回复。

发表回复点击此处取消回复。