神经网络使用随机梯度下降法进行训练,并且在设计和配置模型时需要选择一个损失函数。
有很多损失函数可供选择,知道选择哪个,甚至损失函数是什么以及它在训练神经网络时所起的作用,都可能是一个挑战。
在本文中,您将了解损失和损失函数在训练深度学习神经网络中的作用,以及如何为您的预测建模问题选择正确的损失函数。
阅读本文后,你将了解:
- 神经网络通过优化过程进行训练,该过程需要损失函数来计算模型误差。
- 最大似然为选择神经网络和一般机器学习模型的训练损失函数提供了框架。
- 交叉熵和均方误差是训练神经网络模型时使用的两种主要损失函数。
用我的新书《更好的深度学习》来启动你的项目,书中包含分步教程和所有示例的 Python 源代码文件。
让我们开始吧。

训练深度学习神经网络的损失和损失函数
照片由 Ryan Albrey 拍摄,保留部分权利。
概述
本教程分为七个部分,它们是:
- 神经网络学习作为优化
- 什么是损失函数和损失?
- 最大似然
- 最大似然与交叉熵
- 使用哪个损失函数?
- 如何实现损失函数
- 损失函数和报告的模型性能
我们将重点关注损失函数背后的理论。
有关选择和实现不同损失函数的帮助,请参阅帖子
神经网络学习作为优化
深度学习神经网络学习从训练数据中映射一组输入到一组输出。
我们无法计算神经网络的完美权重;未知数太多。相反,学习问题被视为搜索或优化问题,并使用算法来导航模型可能使用的各种权重集合的空间,以便做出良好或足够好的预测。
通常,神经网络模型使用随机梯度下降优化算法进行训练,并使用误差反向传播算法更新权重。
梯度下降中的“梯度”指的是误差梯度。使用给定权重集合的模型用于进行预测,并计算这些预测的误差。
梯度下降算法试图改变权重,以便下次评估可以减少误差,这意味着优化算法沿着误差的梯度(或斜率)向下导航。
现在我们知道了训练神经网络是解决优化问题,我们可以看看给定权重集合的误差是如何计算的。
想要通过深度学习获得更好的结果吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
什么是损失函数和损失?
在优化算法的上下文中,用于评估候选解(即一组权重)的函数称为目标函数。
我们可以寻求最大化或最小化目标函数,这意味着我们正在寻找一个得分最高或最低的候选解。
通常,对于神经网络,我们寻求最小化误差。因此,目标函数通常被称为成本函数或损失函数,损失函数计算的值简称为“损失”。
我们想要最小化或最大化的函数称为目标函数或标准。当我们最小化它时,我们也可以称之为成本函数、损失函数或误差函数。
— 第 82 页,《深度学习》,2016。
成本或损失函数有一个重要的工作,那就是它必须忠实地将模型的所有方面提炼成一个数字,这样该数字的改进就标志着一个更好的模型。
成本函数将一个可能复杂的系统的各种好坏方面归结为一个数字,一个标量值,这使得候选解能够被排序和比较。
— 第 155 页,《神经网络:前馈人工神经网络的监督学习》,1999。
在优化过程中计算模型误差时,必须选择一个损失函数。
这可能是一个具有挑战性的问题,因为函数必须捕捉问题的特性,并且需要考虑对项目和利益相关者很重要的问题。
因此,重要的是函数要忠实地代表我们的设计目标。如果我们选择了糟糕的误差函数并获得了不满意结果,那将是我们未能正确指定搜索目标的过错。
— 第 155 页,《神经网络:前馈人工神经网络的监督学习》,1999。
现在我们熟悉了损失函数和损失,我们需要知道要使用什么函数。
最大似然
有许多函数可以用来估计神经网络中一组权重的误差。
我们倾向于使用一个函数,其中候选解的空间映射到一个平滑的(但高维的)景观,优化算法可以通过迭代更新模型权重来合理地导航。
最大似然估计,或 MLE,是用于从历史训练数据中寻找参数最佳统计估计的推理框架:这正是我们用神经网络试图做的事情。
最大似然通过最大化从训练数据导出的似然函数来寻找参数的最佳值。
— 第 39 页,《模式识别神经网络》,1995。
我们有一个包含一个或多个输入变量的训练数据集,并且我们需要一个模型来估计模型权重参数,这些参数能最好地将输入的示例映射到输出或目标变量。
给定输入,模型正在尝试做出与目标变量的数据分布相匹配的预测。在最大似然下,损失函数用于估计模型预测的分布与训练数据中目标变量的分布匹配的程度。
最大似然估计的一种解释方式是将其视为最小化由训练集定义的经验分布 [...] 和模型分布之间的不相似性,其中衡量两个分布之间不相似性的程度是 KL 散度。 [...] 最小化此 KL 散度等同于最小化分布之间的交叉熵。
— 第 132 页,《深度学习》,2016。
使用最大似然作为估计神经网络和一般机器学习模型参数(权重)的框架的一个好处是,随着训练数据集中示例数量的增加,模型参数的估计会得到改进。这被称为“一致性”属性。
在适当的条件下,最大似然估计量具有一致性属性 [...],这意味着随着训练示例的数量趋于无穷大,参数的最大似然估计会收敛到参数的真实值。
— 第 134 页,《深度学习》,2016。
现在我们熟悉了最大似然的一般方法,我们可以看一下误差函数。
最大似然与交叉熵
在最大似然框架下,使用 交叉熵 来衡量两个概率分布之间的误差。
在对分类问题建模时,我们有兴趣将输入变量映射到类别标签,我们可以将问题建模为预测一个示例属于每个类别的概率。在二元分类问题中,将有两个类别,因此我们可以预测该示例属于第一个类别的概率。对于多类分类,我们可以为该示例属于每个类别的概率进行预测。
在训练数据集中,一个示例属于给定类别的概率将是 1 或 0,因为训练数据集中的每个样本都是该领域的已知示例。我们知道答案。
因此,在最大似然估计下,我们将寻求一组模型权重,以最小化模型对给定数据集的预测概率分布与训练数据集中概率分布之间的差异。这称为交叉熵。
在大多数情况下,我们的参数模型定义了一个分布 [...],我们只需使用最大似然原理。这意味着我们使用训练数据和模型预测之间的交叉熵作为成本函数。
— 第 178 页,《深度学习》,2016。
严格来说,交叉熵来自信息论领域,单位是“bits”。它用于估计估计概率分布和预测概率分布之间的差异。
在回归问题中,当预测一个数量时,通常使用均方误差(MSE)损失函数。
一些基本函数非常常用。均方误差对于函数逼近(回归)问题很受欢迎 [...] 交叉熵误差函数通常用于输出被解释为属于指示类别的概率的分类问题。
— 第 155-156 页,《神经网络:前馈人工神经网络的监督学习》,1999。
然而,在最大似然估计框架下,并假设目标变量服从高斯分布,均方误差可以被视为模型预测分布与目标变量分布之间的交叉熵。
许多作者使用“交叉熵”一词特指伯努利或 softmax 分布的负对数似然,但这是一种误称。任何由负对数似然组成的损失都是由训练集定义的经验分布与模型定义的概率分布之间的交叉熵。例如,均方误差是经验分布与高斯模型之间的交叉熵。
— 第 132 页,《深度学习》,2016。
因此,在使用最大似然估计框架时,我们将实现一个交叉熵损失函数,在实践中这通常意味着分类问题的交叉熵损失函数和回归问题的均方误差损失函数。
几乎普遍地,深度学习神经网络在最大似然框架下使用交叉熵作为损失函数进行训练。
大多数现代神经网络都使用最大似然进行训练。这意味着成本函数 [...] 被描述为训练数据和模型分布之间的交叉熵。
— 第 178-179 页,《深度学习》,2016。
事实上,采用这种框架可以被认为是深度学习的一个里程碑,因为在完全正式化之前,用于分类的神经网络有时会使用均方误差损失函数。
这些算法更改之一是用交叉熵系列损失函数替换了均方误差。均方误差在 20 世纪 80 年代和 90 年代很受欢迎,但随着统计学界和机器学习界思想的传播,它逐渐被交叉熵损失和最大似然原理所取代。
— 第 226 页,《深度学习》,2016。
最大似然方法几乎被普遍采用,不仅是因为理论框架,主要是因为其产生的成果。具体来说,使用输出层 sigmoid 或 softmax 激活函数的分类神经网络在使用交叉熵损失函数时学习更快、更鲁棒。
使用交叉熵损失函数大大提高了具有 sigmoid 和 softmax 输出的模型的性能,而这些模型以前在使用均方误差损失时遇到了饱和和学习缓慢的问题。
— 第 226 页,《深度学习》,2016。
使用哪个损失函数?
我们可以总结上一节,并直接建议在最大似然框架下您应该使用的损失函数。
重要的是,损失函数的选择直接关系到您的神经网络输出层使用的激活函数。这两个设计元素是相互关联的。
将输出层配置视为选择预测问题的框架,而损失函数的选择是计算给定问题框架下误差的方法。
成本函数的选择与输出单元的选择紧密耦合。大多数时候,我们只是使用数据分布和模型分布之间的交叉熵。选择如何表示输出然后决定交叉熵函数的格式。
— 第 181 页,《深度学习》,2016。
我们将根据输出层和损失函数回顾每种问题类型的最佳实践或默认值。
回归问题
您预测一个实数值的问题。
- 输出层配置:一个带有线性激活单元的节点。
- 损失函数:均方误差(MSE)。
二分类问题
您将一个示例分类为属于两个类别之一的问题。
该问题被表述为预测一个示例属于类别一的概率,例如您为其分配整数值 1 的类别,而另一个类别被分配值 0。
- 输出层配置:一个带有 sigmoid 激活单元的节点。
- 损失函数:交叉熵,也称为对数损失。
多类别分类问题
您将一个示例分类为属于两个以上类别之一的问题。
该问题被表述为预测一个示例属于每个类别的概率。
- 输出层配置:每个类别使用 softmax 激活函数的一个节点。
- 损失函数:交叉熵,也称为对数损失。
如何实现损失函数
为了使损失函数具体化,本节解释了每种主要类型的损失函数如何工作以及如何在 Python 中计算得分。
均方误差损失
均方误差损失,简称 MSE,计算为预测值和实际值之间平方差的平均值。
无论预测值和实际值的符号如何,结果始终为正,并且完美值为 0.0。损失值被最小化,尽管它也可以通过使分数变负来进行最大化优化过程。
下面的 Python 函数提供了计算实际和预测实值数量列表的均方误差的伪代码式的可工作实现。
|
1 2 3 4 5 6 7 |
# 计算均方误差 def mean_squared_error(actual, predicted): sum_square_error = 0.0 for i in range(len(actual)): sum_square_error += (actual[i] - predicted[i])**2.0 mean_square_error = 1.0 / len(actual) * sum_square_error return mean_square_error |
为了高效实现,我建议您使用 scikit-learn 的 mean_squared_error() 函数。
交叉熵损失(或对数损失)
交叉熵损失通常简称为“交叉熵”、“对数损失”、“逻辑损失”或简称为“log loss”。
将每个预测概率与实际类别输出值(0 或 1)进行比较,并计算一个分数,该分数根据与期望值的距离对概率进行惩罚。惩罚是对数的,对小差异(0.1 或 0.2)给出小分数,对大差异(0.9 或 1.0)给出巨大分数。
交叉熵损失被最小化,其中较小的值表示比较大的值更好的模型。完美预测概率的模型具有 0.0 的交叉熵或对数损失。
交叉熵对于二元或二类别预测问题实际上是计算所有示例的平均交叉熵。
下面的 Python 函数提供了一个伪代码式的可工作实现,用于计算实际的 0 和 1 值与类别 1 的预测概率之间的交叉熵。
|
1 2 3 4 5 6 7 8 9 |
from math import log # 计算二元交叉熵 def binary_cross_entropy(actual, predicted): sum_score = 0.0 for i in range(len(actual)): sum_score += actual[i] * log(1e-15 + predicted[i]) mean_sum_score = 1.0 / len(actual) * sum_score return -mean_sum_score |
注意,我们在预测概率中添加了一个非常小的值(此处为 1E-15),以避免计算 log(0.0)。这意味着在实践中,最佳损失值将非常接近零,但不是零。
交叉熵可以为多类别分类计算。类别已被进行独热编码,这意味着每个类别值都有一个二进制特征,并且预测必须为每个类别提供预测概率。然后,交叉熵将跨每个二进制特征进行求和,并跨数据集中的所有示例进行平均。
下面的 Python 函数提供了伪代码式的可工作实现,用于计算实际的独热编码值与每个类别的预测概率之间的交叉熵。
|
1 2 3 4 5 6 7 8 9 10 |
from math import log # 计算分类交叉熵 def categorical_cross_entropy(actual, predicted): sum_score = 0.0 for i in range(len(actual)): for j in range(len(actual[i])): sum_score += actual[i][j] * log(1e-15 + predicted[i][j]) mean_sum_score = 1.0 / len(actual) * sum_score return -mean_sum_score |
为了高效实现,我建议您使用 scikit-learn 的 log_loss() 函数。
损失函数和报告的模型性能
在最大似然框架下,我们知道我们想在随机梯度下降中使用交叉熵或均方误差损失函数。
然而,我们可能想使用损失函数报告模型性能,也可能不想。
例如,对数损失难以解释,特别是对于非机器学习从业者。均方误差也是如此。相反,报告分类和回归模型所用的准确率和均方根误差可能更重要。
根据这些指标而不是损失来选择模型也是可取的。这是一个重要的考虑因素,因为具有最小损失的模型可能不是具有对项目利益相关者重要的最佳指标的模型。
一个好的划分是使用损失来评估和诊断模型学习得有多好。这包括优化过程的所有考虑因素,例如过拟合、欠拟合和收敛。然后可以选择一个对项目利益相关者有意义的替代指标,用于评估模型性能和执行模型选择。
- 损失:仅用于评估和诊断模型优化。
- 指标:用于在项目背景下评估和选择模型。
同一指标可以用于这两种考虑,但优化过程的考虑因素与项目目标不同的可能性更大,并且需要不同的分数。尽管如此,改进损失通常也能改进或最差地不影响感兴趣的指标。
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
书籍
- 深度学习, 2016.
- 《神经网络精工:前馈人工神经网络中的监督学习》, 1999.
- 《用于模式识别的神经网络》, 1995.
文章
总结
在本文中,您了解了损失和损失函数在训练深度学习神经网络中的作用,以及如何为您的预测建模问题选择正确的损失函数。
具体来说,你学到了:
- 神经网络通过优化过程进行训练,该过程需要损失函数来计算模型误差。
- 最大似然为选择神经网络和一般机器学习模型的训练损失函数提供了框架。
- 交叉熵和均方误差是训练神经网络模型时使用的两种主要损失函数。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。




您的交叉熵伪代码中是否缺少了 (1 – actual[i]) * log(1 – (1e-15 + predicted[i])) 这一项?我认为没有它,当实际值为零时,分数将始终为零。
我不这么认为,当进行评估时,结果与 sklearn 的 log_loss() 指标直接比较。
https://scikit-learn.cn/stable/modules/generated/sklearn.metrics.log_loss.html
嗯,也许我的例子是错的?当我使用 sklearn 的函数时,我得到的结果不同。
See also the sklearn source code
https://github.com/scikit-learn/scikit-learn/blob/7389dba/sklearn/metrics/classification.py#L1710
https://github.com/scikit-learn/scikit-learn/blob/7389dba/sklearn/metrics/classification.py#L1786
https://github.com/scikit-learn/scikit-learn/blob/7389dba/sklearn/metrics/classification.py#L1797
Might be something funky with your test.
The results appear to match in my test
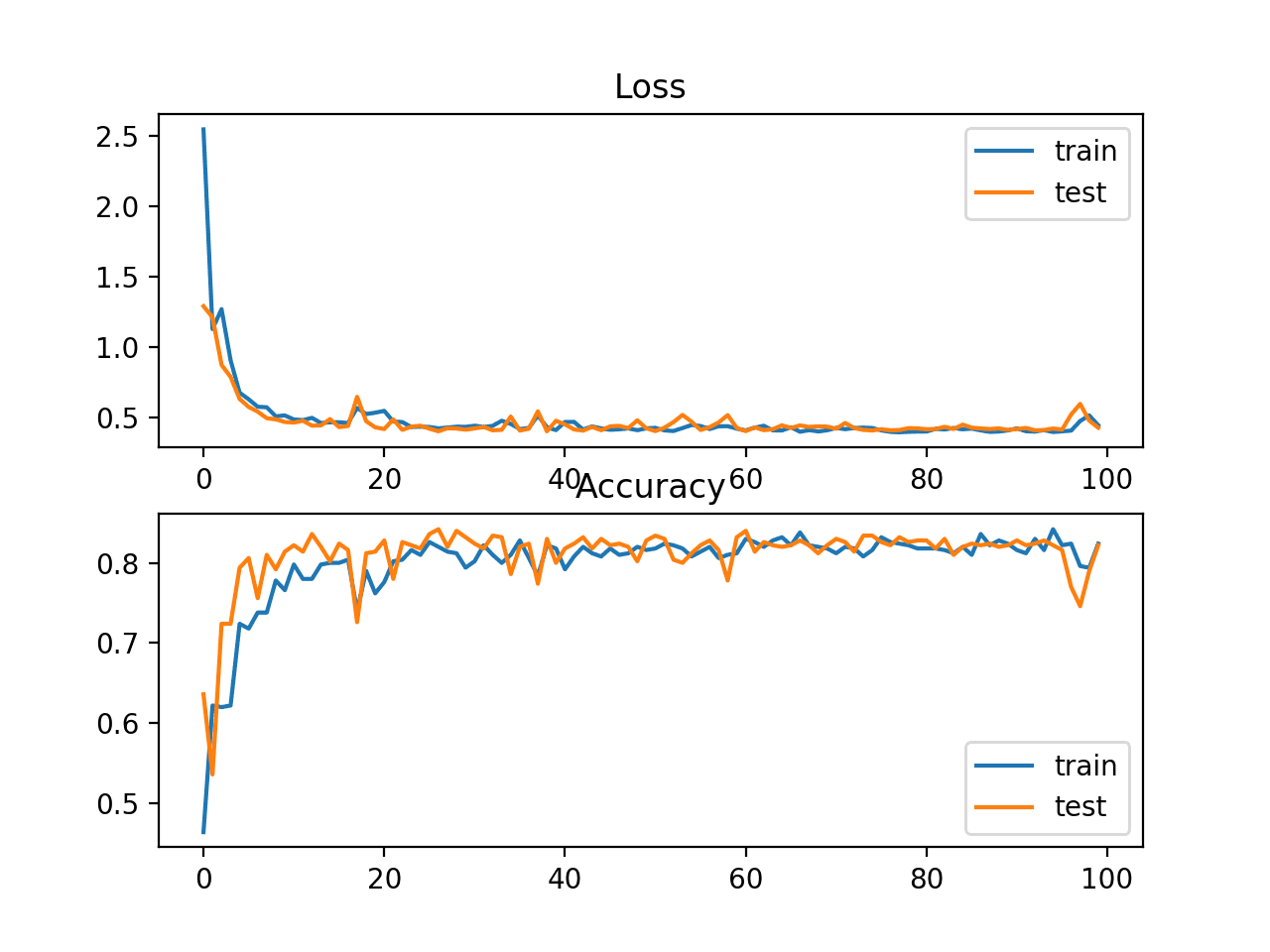
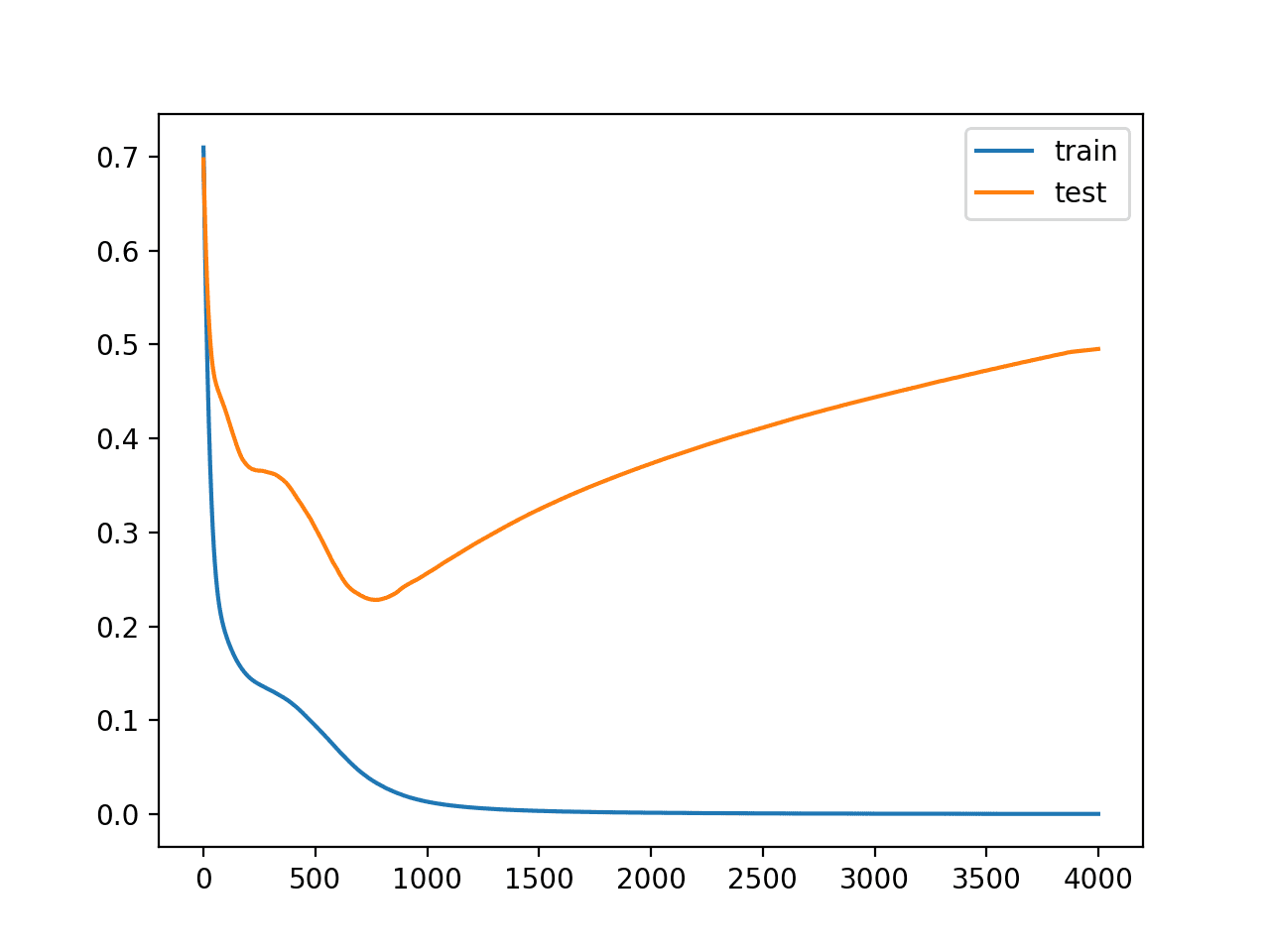
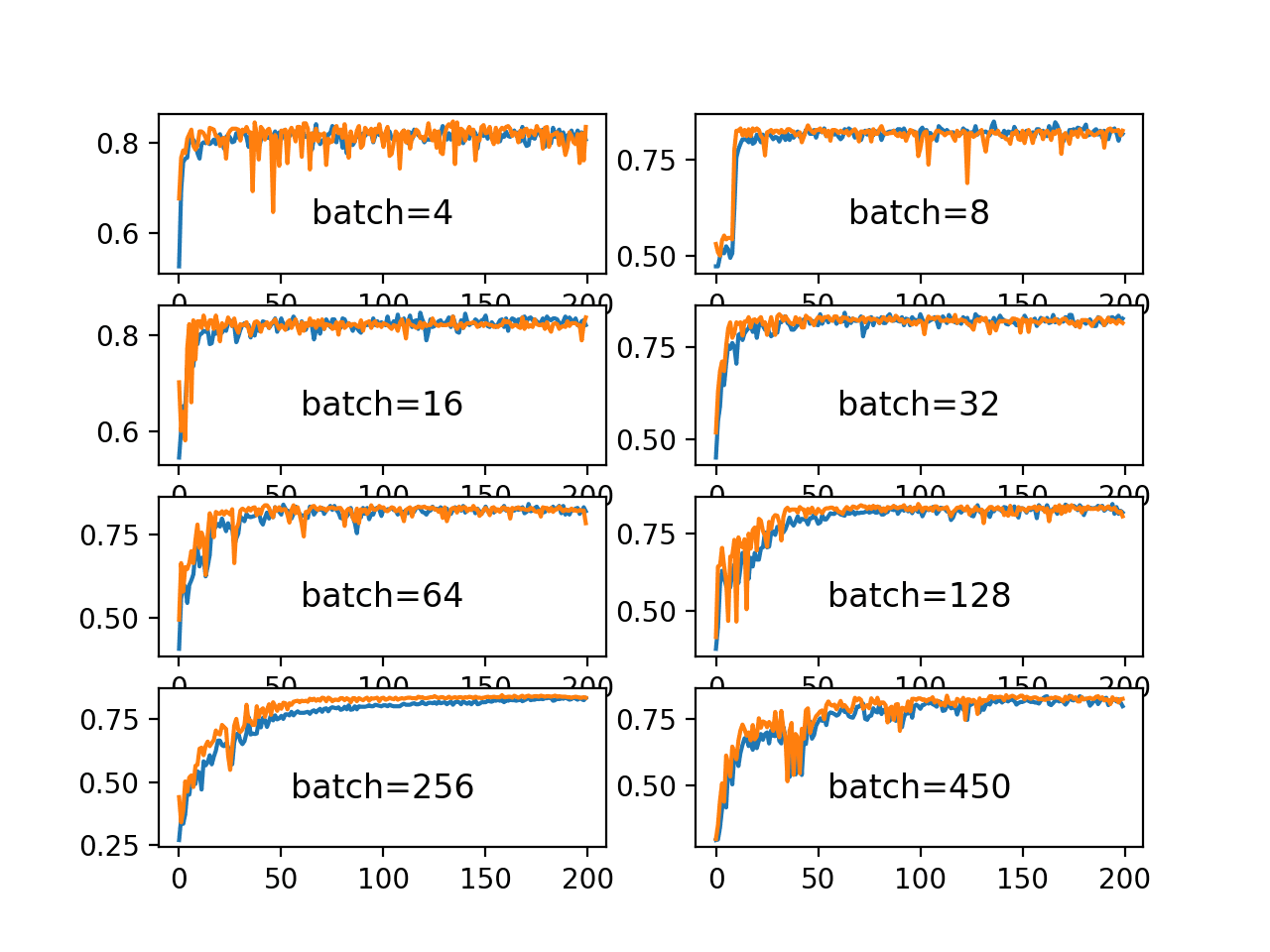
结果
Julian, you only need 1e-15 for values of 0.0. Thus, if you do an if statement or simply subtract 1e-15 you will get the result. That is
binary_cross_entropy([1, 0, 1, 0], [1-1e-15, 1-1e-15, 1-1e-15, 0])
Thanks for the tip Zach!
HI I think you’re missing a term in your binary cross entropy code snippet
((1 – actual[i]) * log(1 – (1e-15 + predicted[i])))
As represented in the
(1 – yt) log(1 – yp))
part in the binary cross entropy formula as shown in the sklearn docs
-log P(yt|yp) = -(yt log(yp) + (1 – yt) log(1 – yp))
https://scikit-learn.cn/stable/modules/generated/sklearn.metrics.log_loss.html
from math import log
# 计算二元交叉熵
def binary_cross_entropy(actual, predicted)
sum_score = 0.0
for i in range(len(actual))
sum_score += (actual[i] * log(1e-15 + predicted[i])) + ((1 – actual[i]) * log(1 – (1e-15 + predicted[i])))
mean_sum_score = 1.0 / len(actual) * sum_score
return -mean_sum_score
Thanks, this might be a better description
https://machinelearning.org.cn/cross-entropy-for-machine-learning/
Your test works as long as the elements in each array of
predictedadd up to 1. Do they have to? In the sklearn test suite, they don’t always: https://github.com/scikit-learn/scikit-learn/blob/037ee933af486a547ee0c70ea27cdbcdf811fa11/sklearn/metrics/tests/test_classification.py#L1756When they don’t, you get different results than sklearn. Try with these values
actual = [[1.0, 0.0, 0.0], [0.0, 1.0, 0.0], [0.0, 0.0, 1.0]]
predicted = [[0.9, 0.05, 0.05], [0.1, 0.8, 0.2], [0.1, 0.2, 0.7]]
mine
0.22839300363692153
sklearn
0.2601630635716978
Yes, they are probabilities.
So in conclusion about the relationship between Maximum likelihood, Cross-Entropy and MSE is
├── Maximum likelihood: provides a framework for choosing a loss function
| ├── Cross-Entropy: for classification problems
| └── MSE: for regression problems
Is it right?
正确。
嗨,Jason,
Thanks again for the great tutorials.
What about rules for using auxiliary loss (/auxiliary classifiers)?
Do you have any tutorial on that? It seems this strategy is not so common presently.
Sorry, what do you mean exactly by “auxiliary loss”?
I am a student of classification but now want to
know about NEURAL NETWORK
您可以从这里开始
https://machinelearning.org.cn/start-here/#deeplearning
嗨,Jason,
I mean the other losses introduced when building multi-input and multi-output models (=auxiliary classifiers) as shown in keras functional-api-guide. Inception uses this strategy but it seems it’s no so common somehow. Did you write about this?
谢谢
Sorry, I don’t have any tutorials on this topic, perhaps in the future.
Best articles you publish and you do it for good. Awesome job.
谢谢,我很高兴它有所帮助!
嗨,Jason,
do we need to calculate mean squared error(mse), using function(as you defined above)?
I have seen parameter loss=’mse’ while we compile the model.
No, if you are using keras, you can specify ‘mse’.
嗨,Jason,
In a regression problem, how do you have a convex cost/loss function? The MSE is not convex given a nonlinear activation function. Thanks.
嗨,Jason,
Thank you for the great article. I have one query, suppose we have to predict the location information in terms of the Latitude and Longitude for a regression problem. How we have to define the loss function for training the neural network?
Perhaps try MSE?
So, I have a question . To calculate mse, we make predictions on the training data, not test data. Right ?
We calculate loss on the training dataset during training.
After training, we can calculate loss on a test set.
What do you mean by loss on a test set ?
The loss function used to train the model calculated for predictions on the test set.
Hello Jason. Can we have a negative loss values when training using a negative log likelihood loss function?
I am training an LSTM with the last layer as a mixture layer which has to do with probability.
Training with only LSTM layers, I never get a negative loss but when the addition layer is added, I get negative loss values. In your experience, do you think this is right or even possible? Thanks.
No, perfect loss is 0.
Okay thanks. I did search online more extensively and the founder of Keras did say it is possible. Also, in one of your tutorials, you got negative loss when using cosine proximity
https://machinelearning.org.cn/custom-metrics-deep-learning-keras-python/
Fair enough. I was thinking more cross-entropy and mse – used on almost all classification and regression tasks respectively, both are never negative.
谢谢 Jason
不客气!
嗨,Jason,
I need a suggestion.
I am working on a regression problem with the output layer having 4 nodes. I used Huber loss function just to avoid outliers in my data generated(inverse problem) and because MSE as a loss function will not do too well with outliers in my data.
However, whenever I calculate the mean error and variance error, I have the variance error being lesser than the mean error. I want to know if that it’s possible because my supervisor says otherwise(var error > mean error)
I also tried to check for over-fitting and under-fitting and it looks good.
If your model has a high variance, perhaps try fitting multiple copies of the model with different initial weights and ensemble their predictions.
Actually for each model, I used different weight initializers and it still gives the same output error for the mean and variance.
I don’t think it’s is a high variance issue because from my plot, it doesn’t show a high training or testing error.
Perhaps experiment/prototype to help uncover the cause of your issue. Not sure I have much to add off the cuff, sorry.
okay, I will need to send you some datasets and the network architecture.
How I send you the datasets?
Sorry, I don’t have the capacity to review your code and dataset.
Perhaps you can summarize your problem in a sentence or two?
嗨,Jason,
I have a question about calculating loss in online learning scheme. Since ANN learns after every forward/backward pass what is the good way to calculate the loss on the entire training set?
Make only forward pass at some point on the entire training set? Is there is some cheaper approximation? A similar question stands for a mini-batch.
谢谢
The loss is the mean error across samples for each each update (batch) or averaged across all updates for the samples (epoch).
I have trained a CNN model for binary image classification problem. As binary cross entropy was giving a less accuracy, I proposed a custom loss function which is given below.
custom_loss(true_labels,predictions)= metrics.mean_squared_error(true_labels, predictions) + 0.1*K.mean(true_labels – predictions)
Now clearly this loss function is using MSE ….so my problem is how can I justify the better accuracy given by this custom loss function as it is using MSE. Please help I am really stuck.
You can run a careful repeated evaluation experiment on the same test harness using each loss function and compare the results using a statistical hypothesis test. That would be enough justification to use one model over another.
In terms of further justification – e.g, theoretical, why bother? Just use the model that gives the best performance and move on to the next project.
Thank you so much for your response. The problem is that this research is for a research paper where I have to theoretically justify it. I would highly appreciate any help in this regard.
Sorry, I don’t have the capacity to help you with your research paper – I teach applied machine learning.
Perhaps discuss it with your research advisor.
Hey, can anyone help me with the back propagation equations with using MSE as the cost function, for a multiple hidden NN layer model? I used dL/dAL= 2*(AL-Y) as the derivative of the loss function w.r.t the predicted value but am getting same prediction for all data points. Here, AL is the activation output vector of the output layer and Y is the vector containing original values. I used tanh function as the activation function for each layer and the layer config is as follows= (4,10,10,10,1)
Equations are listed here
https://en.wikipedia.org/wiki/Backpropagation
when the probabilities match between the true values and the predicted values, the cross entropy should be the minimum, which equals to the entropy. The log loss, or cross entropy loss, actually refers to the KL divergence, right?
Cross entropy can be calculated using KL Divergence, but is not the same as the KL Divergence, you can learn more here
https://machinelearning.org.cn/cross-entropy-for-machine-learning/
嗨,Jason,
I want to thank you so much for the beautiful tutorials/examples you have provided.
I am one that learns best when I have a good example to look at.
When working with multi-class logistic regression, I get lost in determining what
to do next with the (error or loss) output of the “categorical cross entropy” function.
I can’t find any examples anywhere on how to update coefficients/weights with the “error”
from the “categorical cross entropy” function. Your Keras tutorial handles it really
well; however there is no detail because it all happens inside Keras.
The best I can do is look at your “Logistic regression for two-class problems” and build
from there. In the 2-class example you use the error to update the coefficients
(in stochastic gradient decent) as follows
for row in train
yhat = predict(row, coef)
error = row[-1] – yhat
coef[0] = coef[0] + l_rate * error * yhat * (1.0 – yhat)
for i in range(len(row)-1)
coef[i + 1] = coef[i + 1] + l_rate * error * yhat * (1.0 – yhat) * row[i]
building from your example I tried to adjust it for multi-class. Here’s what I came up
用
coef = [[0.0 for i in range(len(train[0]))] for j in range(n_class)]
.....
actual = []
predicted = []
for row in train
j1 = int(row[-1])
yval= [0 for j2 in range(n_class)]
yval[j1] = 1
yhat = predictSoftmax(row, coef)
actual.append(yval)
predicted.append(yhat)
error = categorical_cross_entropy(actual, predicted)
coef[j1][0] = coef[j1][0] + l_rate * error * yhat[j1] * (1.0 – yhat[j1])
for i in range(len(row)-1)
coef[j1][i + 1] = coef[j1][i + 1] + l_rate * error * yhat[j1] * (1.0 – yhat[j1]) * row[i]
for j in range(n_class)
if j1 != j
coef[j][0] = coef[j][0] + l_rate * error * -1.00 * yhat[j] * (1.0 – yhat[j])
for i in range(len(row)-1)
coef[j][i + 1] = coef[j][i + 1] + l_rate * error * -1.00 * yval[j] * (1.0 – yhat[j]) * row[i]
我运行的测试结果与您 Keras 的示例结果相似
(但要慢得多);但是,我不太确定我是否走在正确的道路上。
你能帮忙吗?
抱歉,我没有能力审查/调试您的代码。
通常,您希望在模型中使用多项概率分布,例如多项逻辑回归。sklearn 有一个示例 – 或许可以先查看库中的代码作为第一步。
https://machinelearning.org.cn/multinomial-logistic-regression-with-python/
您能否建议我使用哪种误差函数,如果涉及两个参数,其中一个需要最小化,另一个需要最大化?
我们可以将参数假定为( y1_pred, y2_pred, y1_actual, y2_actual)。
也许您需要设计自己的误差函数?
亲爱的 Jason,
我正在处理一个神经网络,它以一个输入层开始,然后分支到 4 个不同的分支。所有四个分支的最终预测被融合在一起得到最终预测。为了检查每个分支的性能,我想在最终预测之前计算每个分支的损失。那么,这是否可以使用 Keras 或任何低级方法来实现?
是的,您可以使用函数式 API 来做到这一点。
嗨,杰森,
多阶段分类问题,可以使用什么损失函数?
分类交叉熵。
谢谢 Jason。
不客气。
Jason,您会推荐哪些进一步的阅读或内容来了解不同的回归案例?我想使用 RNN 来预测每小时的温度。这些数据是平稳的(实际上,每天它会形成几乎相同的钟形曲线)。我认为最小化预测值和目标值之间的最大绝对差值会很好。但是,您能推荐什么损失函数?
这是一个很好的起点。
https://machinelearning.org.cn/start-here/#deep_learning_time_series
你好,
如果我们的损失函数有多个部分,并且它是损失的加权组合,我们如何为每个损失函数找到合适的系数?您有什么建议吗?有没有办法自动找到每个部分的最佳权重?
通常,模型是针对单个损失函数进行拟合的。
模型权重是通过随机梯度下降和反向传播找到的。
嗨,Jason,
这可能是一个奇怪的问题。但是,如果您必须使用 sigmoid 函数与 rmse 和 mse,在什么情况下您会使用它?
任何解释都将不胜感激。
在训练机器学习模型时,损失函数和梯度下降哪个先发生?
你好 Grace…以下信息可能有助于澄清
https://machinelearning.org.cn/gradient-descent-for-machine-learning/