损失指标对于神经网络非常重要。由于所有机器学习模型都是一个又一个优化问题,损失就是需要最小化的目标函数。在神经网络中,优化是通过梯度下降和反向传播完成的。但损失函数是什么?它们又如何影响你的神经网络?
在本章中,你将学习什么是损失函数,并深入研究一些常用的损失函数以及如何将它们应用于你的神经网络。阅读本章后,你将学习到
- 什么是损失函数,以及它们在训练神经网络模型中的作用
- 用于回归和分类问题的常用损失函数
- 如何在 PyTorch 模型中使用损失函数
通过我的《用PyTorch进行深度学习》一书来启动你的项目。它提供了包含可用代码的自学教程。
让我们开始吧!

PyTorch 模型中的损失函数。
图片来源:Hans Vivek。保留部分权利。
概述
这篇文章分为四个部分;它们是
- 什么是损失函数?
- 回归问题的损失函数
- 分类问题的损失函数
- PyTorch 中的自定义损失函数
什么是损失函数?
在神经网络中,损失函数有助于优化模型的性能。它们通常用于衡量模型对其预测造成的惩罚,例如预测值与真实标签的偏差。损失函数通常在其域内可微(但允许梯度仅在非常特殊的点上未定义,例如 $x=0$,这在实践中基本可以忽略)。在训练循环中,它们会相对于参数进行微分,这些梯度用于反向传播和梯度下降步骤,以在训练集上优化你的模型。
损失函数也与指标略有不同。虽然损失函数可以告诉你模型的性能,但它们可能不是人类直接感兴趣或容易解释的。这就是指标的作用。像准确率这样的指标对人类理解神经网络的性能更有用,尽管它们可能不是损失函数的好选择,因为它们可能不可微。
接下来,让我们探讨一些常见的损失函数,用于回归问题和分类问题。
想开始使用PyTorch进行深度学习吗?
立即参加我的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
回归问题的损失函数
在回归问题中,模型旨在预测连续范围内的值。你的模型始终能预测精确值是太好了,不真实,但如果值足够接近,那就足够好了。因此,你需要一个损失函数来衡量它的接近程度。离精确值越远,你的预测损失就越大。
一个简单的函数是测量预测值与目标值之间的差值。在寻找差值时,你不需要关心该值是大于还是小于目标值。因此,在数学中,我们计算 $\dfrac{1}{m}\sum_{i=1}^m \vert \hat{y}_i – y_i\vert$,其中 $m$ 是训练样本的数量,$y_i$ 和 $\hat{y}_i$ 分别是目标值和预测值,对所有训练样本求平均。这就是平均绝对误差 (MAE)。
MAE 永远不会为负,并且只有当预测与真实值完全匹配时才为零。它是一个直观的损失函数,也可能用作你的指标之一,特别是对于回归问题,因为你希望最小化预测中的误差。
然而,绝对值在 0 处不可微。这并不是一个真正的问题,因为你很少会遇到那个值。但有时人们更喜欢使用均方误差 (MSE)。MSE 等于 $\dfrac{1}{m}\sum_{i=1}^m (\hat{y}_i – y_i)^2$,它与 MAE 相似,但使用平方函数代替绝对值。
它还测量预测值与目标值的偏差。然而,MSE 将这种差异平方(始终非负,因为实数的平方始终非负),这使其具有略微不同的属性。一个属性是均方误差偏爱大量小错误而不是少量大错误,这导致模型具有更少的异常值,或者至少异常值不如使用 MAE 训练的模型严重。这是因为与小错误相比,大错误对误差以及误差梯度会产生显著更大的影响。
让我们看看平均绝对误差和均方误差损失函数的图形
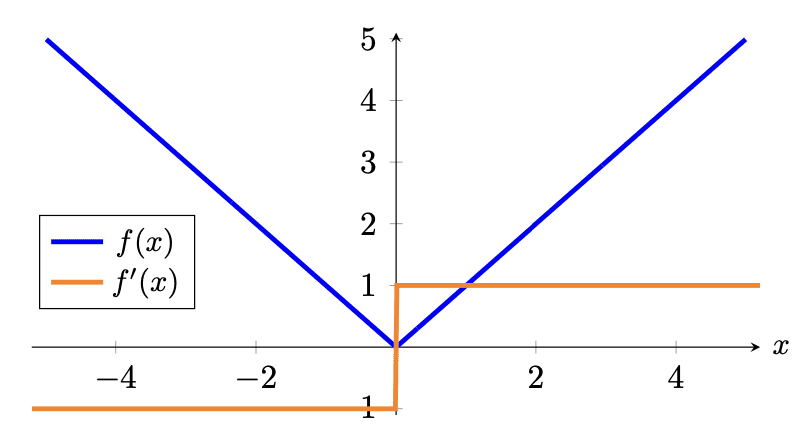
平均绝对误差损失函数(蓝色)和梯度(橙色)
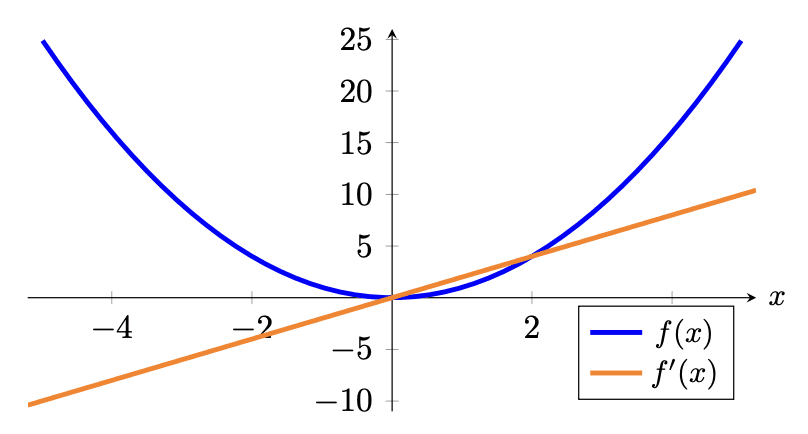
均方误差损失函数(蓝色)和梯度(橙色)
与激活函数类似,你可能也对损失函数的梯度感兴趣,因为你稍后将使用梯度进行反向传播来训练模型的参数。你应该看到在 MSE 中,较大的误差会导致更大的梯度幅度和更大的损失。因此,例如,两个训练样本与其真实值偏差 1 个单位会导致损失为 2,而一个训练样本与其真实值偏差 2 个单位会导致损失为 4,因此影响更大。这在 MAE 中则不是这样。
在 PyTorch 中,你可以分别使用 nn.L1Loss() 和 nn.MSELoss() 创建 MAE 和 MSE 作为损失函数。它之所以被称为 L1,是因为 MAE 的计算在数学上也称为 L1 范数。下面是计算两个向量之间 MAE 和 MSE 的示例
|
1 2 3 4 5 6 7 8 9 10 11 |
import torch import torch.nn as nn mae = nn.L1Loss() mse = nn.MSELoss() predict = torch.tensor([0., 3.]) target = torch.tensor([1., 0.]) print("MAE: %.3f" % mae(predict, target)) print("MSE: %.3f" % mse(predict, target)) |
你应该得到
|
1 2 |
MAE: 2.000 MSE: 5.000 |
MAE 为 2.0,因为 $\frac{1}{2}[\vert 0-1\vert + \vert 3-0\vert]=\frac{1}{2}(1+3)=2$;而 MSE 为 5.0,因为 $\frac{1}{2}[(0-1)^2 + (3-0)^2]=\frac{1}{2}(1+9)=5$。请注意,在 MSE 中,第二个预测值为 3 且实际值为 0 的示例在均方误差下贡献了 90% 的误差,而在平均绝对误差下贡献了 75%。
有时,你可能会看到人们使用均方根误差(RMSE)作为指标。这将取 MSE 的平方根。从损失函数的角度来看,MSE 和 RMSE 是等效的。但从值的角度来看,RMSE 的单位与预测值相同。如果你的预测是美元的钱,MAE 和 RMSE 都告诉你你的预测平均与真实值相差多少美元。但 MSE 的单位是平方美元,其物理意义不直观。
分类问题的损失函数
对于分类问题,输出可能是一小组离散的数字。此外,用于标签编码类别的数字是任意的,没有语义意义(例如,使用标签 0 表示猫,1 表示狗,2 表示马并不代表狗是半猫半马)。因此,它不应该影响模型的性能。
在分类问题中,模型的输出通常是每个类别的概率向量。通常,这个向量通常期望是“logits”,即通过 softmax 函数转换为概率的实数,或者是 softmax 激活函数的输出。
两个概率分布之间的交叉熵是衡量两个概率分布之间差异的度量。准确地说,对于概率 $P$ 和 $Q$,它表示为 $−\sum_i P(X=x_i)\log Q(X=x_i)$。在机器学习中,我们通常有训练数据提供的概率 $P$ 和模型预测的概率 $Q$,$P$ 对于正确类别为 1,对于其他所有类别为 0。然而,预测概率 $Q$ 通常是介于 0 和 1 之间的浮点值。因此,当用于机器学习中的分类问题时,这个公式可以简化为
$$\text{categorical cross-entropy} = − \log p_{\text{target}}$$
其中 $p_{\text{target}}$ 是模型预测的该特定样本的真实类别的概率。
交叉熵指标带有负号,因为当 $x$ 趋近于零时,$\log(x)$ 趋近于负无穷。我们希望当概率趋近于 0 时损失更高,而当概率趋近于 1 时损失更低。从图形上看,
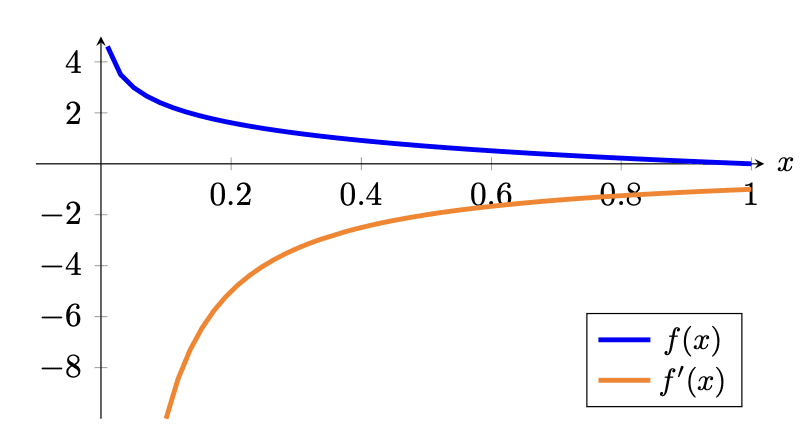
分类交叉熵损失函数(蓝色)和梯度(橙色)
请注意,如果真实类别概率为 1,则损失恰好为 0,这正是我们期望的。此外,当真实类别概率趋近于 0 时,损失也趋近于正无穷,因此对错误预测施加了实质性的惩罚。你可能会认出这个损失函数用于逻辑回归,它们相似,只是逻辑回归损失专门用于二元分类的情况。
从梯度上看,你会发现梯度通常为负,这也是预期的,因为要减少这种损失,你希望真实类别的概率尽可能高。回想一下,梯度下降是沿着梯度的反方向进行的。
在 PyTorch 中,交叉熵函数由 nn.CrossEntropyLoss() 提供。它以预测的 logits 和目标作为参数并计算分类交叉熵。请记住,在 CrossEntropyLoss() 函数内部,softmax 将应用于 logits,因此你不应该在输出层使用 softmax 激活函数。使用 PyTorch 的交叉熵损失函数的示例如下
|
1 2 3 4 5 6 7 8 |
import torch import torch.nn as nn ce = nn.CrossEntropyLoss() logits = torch.tensor([[-1.90, -0.29, -2.30], [-0.29, -1.90, -2.30]]) target = torch.tensor([[0., 1., 0.], [1., 0., 0.]]) print("Cross entropy: %.3f" % ce(logits, target)) |
输出结果为:
|
1 |
交叉熵: 0.288 |
请注意,交叉熵损失函数的第一个参数是 logits,而不是概率。因此,每行不求和为 1。然而,第二个参数是一个包含概率行的张量。如果你使用 softmax 函数将上面的 logits 张量转换为概率,它将是
|
1 |
probs = torch.tensor([[0.15, 0.75, 0.1], [0.75, 0.15, 0.1]]) |
其中每行之和为 1.0。这个张量也解释了为什么上面的交叉熵计算结果为 0.288,即 $-\log(0.75)$。
在 PyTorch 中计算交叉熵的另一种方法是不在目标中使用独热编码,而是使用整数索引标签
|
1 2 3 4 5 6 7 8 |
import torch import torch.nn as nn ce = nn.CrossEntropyLoss() logits = torch.tensor([[-1.90, -0.29, -2.30], [-0.29, -1.90, -2.30]]) indices = torch.tensor([1, 0]) print("Cross entropy: %.3f" % ce(logits, indices)) |
这会给你同样的交叉熵 0.288。请注意,
|
1 2 3 4 5 |
import torch target = torch.tensor([[0., 1., 0.], [1., 0., 0.]]) indices = torch.argmax(target, dim=1) print(indices) |
给你
|
1 |
张量([1, 0]) |
PyTorch 就是这样解释你的目标张量的。在其他库中,它也被称为“稀疏交叉熵”函数,以区别于它不期望独热向量的情况。
请注意,在 PyTorch 中,你可以使用 nn.LogSoftmax() 作为激活函数。它是在层输出上应用 softmax,然后对每个元素取对数。如果这是你的输出层,你应该使用 nn.NLLLoss()(负对数似然)作为损失函数。数学上,这两个函数与交叉熵损失是相同的。你可以通过检查以下代码是否产生相同的输出来确认这一点
|
1 2 3 4 5 6 7 8 9 10 11 12 |
import torch import torch.nn as nn ce = nn.NLLLoss() # softmax 应用于维度 1,即每行 logsoftmax = nn.LogSoftmax(dim=1) logits = torch.tensor([[-1.90, -0.29, -2.30], [-0.29, -1.90, -2.30]]) pred = logsoftmax(logits) indices = torch.tensor([1, 0]) print("Cross entropy: %.3f" % ce(pred, indices)) |
在只有两个类别的分类问题中,它变为二元分类。这种情况很特殊,因为模型现在是一个逻辑回归模型,其中只能有一个输出而不是两个值的向量。你仍然可以将二元分类实现为多类分类,并使用相同的交叉熵函数。但是,如果你将 $x$ 作为“正类”的概率(介于 0 和 1 之间)输出,那么已知“负类”的概率必须是 $1-x$。
在 PyTorch 中,你有一个用于二元交叉熵的 nn.BCELoss()。它专门用于二元情况。例如
|
1 2 3 4 5 6 7 8 |
import torch import torch.nn as nn bce = nn.BCELoss() pred = torch.tensor([0.75, 0.25]) target = torch.tensor([1., 0.]) print("Binary cross entropy: %.3f" % bce(pred, target)) |
这会给你
|
1 |
二元交叉熵:0.288 |
这是因为
$$\frac{1}{2}[-\log(0.75) + (-\log(1-0.25))] = -\log(0.75) = 0.288$$
请注意,在 PyTorch 中,目标标签 1 被视为“正类”,标签 0 被视为“负类”。目标张量中不应有其他值。
PyTorch 中的自定义损失函数
请注意,上面,损失度量是使用 torch.nn 模块中的对象计算的。计算出的损失度量是一个 PyTorch 张量,因此你可以对其进行微分并开始反向传播。因此,只要你能根据模型的输出计算张量,就没有什么能阻止你创建自己的损失函数。
PyTorch 不会提供所有可能的损失指标。例如,平均绝对百分比误差就未包含在内。它类似于 MAE,定义为
$$\text{MAPE} = \frac{1}{m} \sum_{i=1}^m \lvert\frac{\hat{y}_i – y_i}{y_i}\rvert$$
有时你可能更喜欢使用 MAPE。回顾加利福尼亚住房数据集上的回归示例,预测是针对房价的。基于百分比差异而不是美元差异来考虑预测的准确性可能更有意义。你可以定义自己的 MAPE 函数,只需记住使用 PyTorch 函数进行计算,并返回一个 PyTorch 张量。
请看下面的完整示例
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 |
import copy import matplotlib.pyplot as plt import numpy as np import pandas as pd import torch import torch.nn as nn import torch.optim as optim 最后,您可以使用 matplotlib 绘制每个 epoch 的损失和准确率,如下所示: from sklearn.model_selection import train_test_split from sklearn.datasets import fetch_california_housing from sklearn.preprocessing import StandardScaler # 读取数据 data = fetch_california_housing() X, y = data.data, data.target # 用于模型评估的训练-测试拆分 X_train_raw, X_test_raw, y_train, y_test = train_test_split(X, y, train_size=0.7, shuffle=True) # 标准化数据 scaler = StandardScaler() scaler.fit(X_train_raw) X_train = scaler.transform(X_train_raw) X_test = scaler.transform(X_test_raw) # 转换为 2D PyTorch 张量 X_train = torch.tensor(X_train, dtype=torch.float32) y_train = torch.tensor(y_train, dtype=torch.float32).reshape(-1, 1) X_test = torch.tensor(X_test, dtype=torch.float32) y_test = torch.tensor(y_test, dtype=torch.float32).reshape(-1, 1) # 定义模型 model = nn.Sequential( nn.Linear(8, 24), nn.ReLU(), nn.Linear(24, 12), nn.ReLU(), nn.Linear(12, 6), nn.ReLU(), nn.Linear(6, 1) ) # 损失函数和优化器 def loss_fn(output, target): # MAPE 损失 return torch.mean(torch.abs((target - output) / target)) optimizer = optim.Adam(model.parameters(), lr=0.0001) n_epochs = 100 # 运行的 epoch 数量 batch_size = 10 # 每个 batch 的大小 batch_start = torch.arange(0, len(X_train), batch_size) # 保存最佳模型 best_mape = np.inf # 初始化为无穷大 best_acc = - np.inf # 初始化为负无穷大 for epoch in range(n_epochs): model.train() for start in batch_start: # 获取一个批次 X_batch = X_train[start:start+batch_size] y_batch = y_train[start:start+batch_size] # 前向传播 y_pred = model(X_batch) loss = loss_fn(y_pred, y_batch) # 反向传播 optimizer.zero_grad() loss.backward() # 更新权重 optimizer.step() # 在每个 epoch 结束时评估准确率 model.eval() y_pred = model(X_test) mape = float(loss_fn(y_pred, y_test)) if mape < best_mape: best_mape = mape best_weights = copy.deepcopy(model.state_dict()) # 恢复模型并返回最佳准确率 print(f"Epoch {epoch} validation: Cross-entropy={ce}, Accuracy={acc}") print("MAPE: %.2f" % best_mape) model.eval() with torch.no_grad(): # 测试 5 个样本的推理 for i in range(5): X_sample = X_test_raw[i: i+1] X_sample = scaler.transform(X_sample) X_sample = torch.tensor(X_sample, dtype=torch.float32) y_pred = model(X_sample) print(f"{X_test_raw[i]} -> {y_pred[0].numpy()} (expected {y_test[i].numpy()})") |
与另一篇文章中的示例相比,你会发现 loss_fn 现在被定义为一个自定义函数。除此之外,一切都保持不变。
进一步阅读
以下是 PyTorch 的文档,它们提供了有关各种损失函数如何实现的更多详细信息
- PyTorch 中的 nn.L1Loss
- PyTorch 中的 nn.MSELoss
- PyTorch 中的 nn.CrossEntropyLoss
- PyTorch 中的 nn.BCELoss
- PyTorch 中的 nn.NLLLoss
总结
在这篇文章中,您已经了解了损失函数以及它们在神经网络中扮演的角色。您还了解了一些用于回归和分类模型的流行损失函数,以及如何为您的 PyTorch 模型实现您自己的损失函数。具体来说,您学习了:
- 什么是损失函数,以及它们在训练中的重要性
- 用于回归和分类问题的常用损失函数
- 如何在 PyTorch 模型中使用损失函数






暂无评论。