损失度量对于神经网络来说非常重要。由于所有机器学习模型都是一个接一个的优化问题，损失是需要最小化的目标函数。在神经网络中，优化是通过梯度下降和反向传播完成的。但什么是损失函数，它们如何影响你的神经网络？
在本帖中，您将了解损失函数是什么，并深入探讨一些常用的损失函数以及如何将它们应用于您的神经网络。
阅读本文后，您将学到
- 什么是损失函数，它们与度量有何不同
- 回归和分类问题的常用损失函数
- 如何在 TensorFlow 模型中使用损失函数
让我们开始吧！
TensorFlow 中的损失函数
照片来源：Ian Taylor。部分权利保留。
概述
本文分为五个部分；它们是
- 什么是损失函数？
- 平均绝对误差
- 均方误差
- 分类交叉熵
- 损失函数的实际应用
什么是损失函数？
在神经网络中，损失函数有助于优化模型的性能。它们通常用于衡量模型在其预测中产生的一些惩罚，例如预测值与真实标签的偏差。损失函数在其定义域上通常是可微的（但允许在非常特定的点，如 x = 0，梯度未定义，这在实践中基本被忽略）。在训练循环中，它们相对于参数进行微分，这些梯度用于反向传播和梯度下降步骤，以在训练集上优化您的模型。
损失函数与度量也有轻微不同。虽然损失函数可以告诉您模型的性能，但它们可能并不直接引起人类的兴趣或容易被人理解。这就是度量发挥作用的地方。像准确率这样的度量对于人类理解神经网络的性能更有用，尽管它们可能不是损失函数的好选择，因为它们可能不可微。
接下来，让我们探讨一些常见的损失函数：平均绝对误差、均方误差和分类交叉熵。
平均绝对误差
平均绝对误差 (MAE) 衡量预测值与真实标签之间的绝对差值，并计算所有训练样本差值的平均值。数学上，它等于 $\frac{1}{m}\sum_{i=1}^m\lvert\hat{y}_i–y_i\rvert$，其中 $m$ 是训练样本的数量，$y_i$ 和 $\hat{y}_i$ 分别是真实值和预测值，平均到所有训练样本。
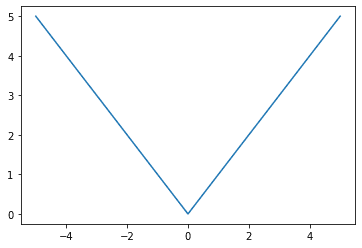
MAE 永远不会为负，并且仅当预测与真实值完全匹配时才会为零。它是一个直观的损失函数，也可以用作您的度量之一，特别适用于回归问题，因为您希望最小化预测中的误差。
让我们看看平均绝对误差损失函数在图形上是什么样子
平均绝对误差损失函数，真实值在 x = 0 处，x 轴表示预测值
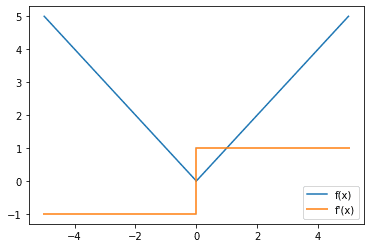
与激活函数类似，您可能也对损失函数的梯度是什么样子感兴趣，因为您稍后会使用梯度进行反向传播来训练模型的参数。
平均绝对误差损失函数（蓝色）和梯度（橙色）
您可能会注意到平均绝对损失函数的梯度存在不连续性。许多人倾向于忽略它，因为它只发生在 x = 0 处，而在实践中，这种情况很少发生，因为在连续分布中，单点的概率非常小。
让我们看看如何使用 Keras 损失模块在 TensorFlow 中实现此损失函数
|
1 2 3 4 5 6 7 8 9 |
import tensorflow as tf from tensorflow.keras.losses import MeanAbsoluteError y_true = [1., 0.] y_pred = [2., 3.] mae_loss = MeanAbsoluteError() print(mae_loss(y_true, y_pred).numpy()) |
这会得到预期的输出 2.0，因为 $ \frac{1}{2}(\lvert 2-1\rvert + \lvert 3-0\rvert) = \frac{1}{2}(4) = 4 $。接下来，让我们探讨另一个具有略微不同特性的回归模型损失函数，即均方误差。
均方误差
另一个流行的回归模型损失函数是均方误差 (MSE)，它等于 $\frac{1}{m}\sum_{i=1}^m(\hat{y}_i–y_i)^2$。它与平均绝对误差类似，因为它也衡量预测值与真实值的偏差。然而，均方误差会将此差值平方（始终为非负，因为实数的平方始终为非负），这使其具有略微不同的特性。
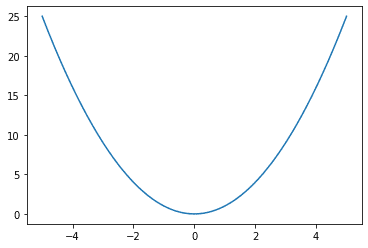
一个值得注意的特点是，均方误差倾向于较多的较小误差而不是较少的较大误差，这会导致模型的外离点更少，或者至少外离点比用平均绝对误差训练的模型更不严重。这是因为与小误差相比，大误差会对误差以及因此产生的误差梯度产生显著更大的影响。
从图形上看，
均方误差损失函数，真实值在 x = 0 处，x 轴表示预测值
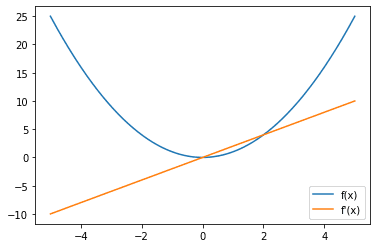
然后，看看梯度，
均方误差损失函数（蓝色）和梯度（橙色）
请注意，较大的误差会导致梯度和损失的幅度更大。因此，例如，两个偏离其真实值的单位误差的训练样本将导致损失为 2，而一个偏离其真实值的单位误差的训练样本将导致损失为 4，因此产生更大的影响。
让我们看看如何在 TensorFlow 中实现均方损失。
|
1 2 3 4 5 6 7 8 9 |
import tensorflow as tf from tensorflow.keras.losses import MeanSquaredError y_true = [1., 0.] y_pred = [2., 3.] mse_loss = MeanSquaredError() print(mse_loss(y_true, y_pred).numpy()) |
这会得到预期的输出 5.0，因为 $\frac{1}{2}[(2-1)^2 + (3-0)^2] = \frac{1}{2}(10) = 5$。请注意，第二个预测值为 3，实际值为 0 的示例在均方误差下贡献了 90% 的误差，而在平均绝对误差下贡献了 75% 的误差。
有时，您可能会看到人们使用均方根误差 (RMSE) 作为度量。这会取 MSE 的平方根。从损失函数的角度来看，MSE 和 RMSE 是等效的。
MAE 和 MSE 都衡量连续范围内的值。因此，它们适用于回归问题。对于分类问题，您可以使用分类交叉熵。
分类交叉熵
前两个损失函数适用于回归模型，其中输出可以是任何实数。然而，对于分类问题，输出可以取一小组离散的数字。此外，用于对类别进行标签编码的数字是任意的，没有语义含义（例如，使用标签 0 代表猫，1 代表狗，2 代表马并不表示狗是猫和马的一半）。因此，它不应影响模型的性能。
在分类问题中，模型的输出是每个类别的概率向量。在 Keras 模型中，此向量通常期望是“logits”，即要使用 softmax 函数转换为概率的实数，或者是一个 softmax 激活函数的输出。
两个概率分布之间的交叉熵是衡量这两个概率分布之间差异的度量。确切地说，对于概率 $P$ 和 $Q$，它等于 $-\sum_i P(X = x_i) \log Q(X = x_i)$。在机器学习中，我们通常有由训练数据提供的概率 $P$，以及由模型预测的 $Q$，其中 $P$ 对于正确类别为 1，对于所有其他类别为 0。然而，预测概率 $Q$ 通常介于 0 和 1 之间。因此，当用于机器学习分类问题时，此公式可以简化为：$$\text{分类交叉熵} = – \log p_{gt}$$其中 $p_{gt}$ 是模型对特定样本的真实类别的预测概率。
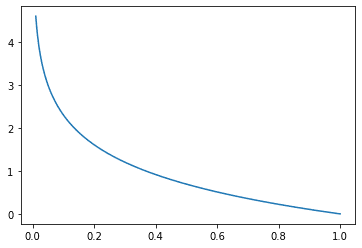
交叉熵度量有一个负号，因为当 $x$ 趋近于零时，$\log(x)$ 趋近于负无穷大。我们希望当概率接近 0 时损失更大，当概率接近 1 时损失更小。从图形上看，
分类交叉熵损失函数，其中 x 是真实类别的预测概率
请注意，当真实类别的概率为 1 时，损失恰好为 0，正如预期的那样。同样，当真实类别的概率趋近于 0 时，损失也趋近于正无穷大，因此会显著惩罚错误的预测。您可能认识到此损失函数用于逻辑回归，它类似，只是逻辑回归损失特定于二元类别的情况。
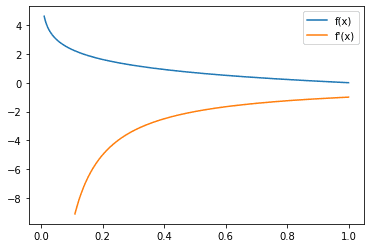
现在，看看交叉熵损失的梯度，
分类交叉熵损失函数（蓝色）和梯度（橙色）
从梯度可以看出，梯度通常为负，这也是预期的，因为为了减小此损失，您希望真实类别的概率尽可能高。回想一下，梯度下降的方向与梯度相反。
在 TensorFlow 中实现分类交叉熵有两种不同的方法。第一种方法将 one-hot 向量作为输入
|
1 2 3 4 5 6 7 8 9 10 |
import tensorflow as tf from tensorflow.keras.losses import CategoricalCrossentropy # 使用 one hot 向量表示 y_true = [[0, 1, 0], [1, 0, 0]] y_pred = [[0.15, 0.75, 0.1], [0.75, 0.15, 0.1]] cross_entropy_loss = CategoricalCrossentropy() print(cross_entropy_loss(y_true, y_pred).numpy()) |
这给出的输出为 0.2876821，正如预期的那样，等于 $-log(0.75)$。在 TensorFlow 中实现分类交叉熵的另一种方法是使用标签编码表示，其中类别由一个表示真实类别的非负整数表示，而不是。
|
1 2 3 4 5 6 7 8 9 |
import tensorflow as tf from tensorflow.keras.losses import SparseCategoricalCrossentropy y_true = [1, 0] y_pred = [[0.15, 0.75, 0.1], [0.75, 0.15, 0.1]] cross_entropy_loss = SparseCategoricalCrossentropy() print(cross_entropy_loss(y_true, y_pred).numpy()) |
这也给出的输出为 0.2876821。
现在您已经了解了回归和分类模型的损失函数，让我们看看如何在机器学习模型中使用它们。
损失函数的实际应用
让我们看看如何在实践中使用损失函数。您将通过一个简单的密集模型在 MNIST 数字分类数据集上进行探索。
首先，从 Keras 数据集模块下载数据
|
1 2 3 |
import tensorflow.keras as keras (trainX, trainY), (testX, testY) = keras.datasets.mnist.load_data() |
然后，构建您的模型
|
1 2 3 4 5 6 7 8 9 10 11 |
from tensorflow.keras import Sequential from tensorflow.keras.layers import Dense, Input, Flatten model = Sequential([ Input(shape=(28,28,1,)), Flatten(), Dense(units=84, activation="relu"), Dense(units=10, activation="softmax"), ]) print (model.summary()) |
并查看上述代码输出的模型架构
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
_________________________________________________________________ 层 (类型) 输出形状 参数数量 ================================================================= flatten_1 (Flatten) (None, 784) 0 dense_2 (Dense) (None, 84) 65940 dense_3 (Dense) (None, 10) 850 ================================================================= 总参数：66,790 可训练参数：66,790 不可训练参数: 0 _________________________________________________________________ |
然后，您可以编译您的模型，这也是您引入损失函数的地方。由于这是一个分类问题，请使用交叉熵损失。特别是，由于 Keras 数据集中的 MNIST 数据集表示为标签而不是 one-hot 向量，因此请使用 SparseCategoricalCrossentropy 损失。
|
1 |
model.compile(optimizer="adam", loss=tf.keras.losses.SparseCategoricalCrossentropy(), metrics="acc") |
最后，您训练您的模型
|
1 |
history = model.fit(x=trainX, y=trainY, batch_size=256, epochs=10, validation_data=(testX, testY)) |
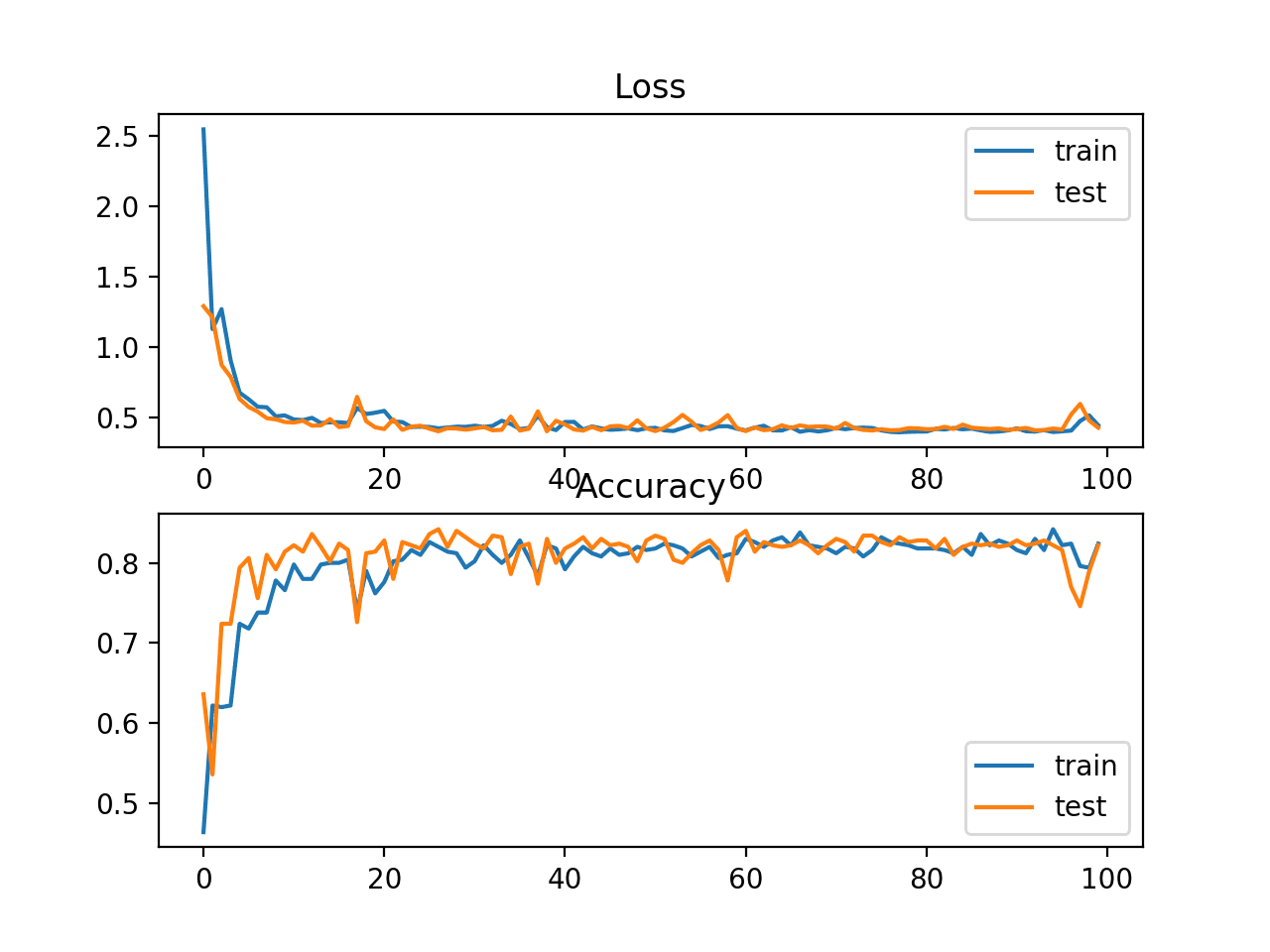
您的模型成功训练，输出如下
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
第 1/10 纪元 235/235 [==============================] - 2s 6ms/step - loss: 7.8607 - acc: 0.8184 - val_loss: 1.7445 - val_acc: 0.8789 第 2/10 纪元 235/235 [==============================] - 1s 6ms/step - loss: 1.1011 - acc: 0.8854 - val_loss: 0.9082 - val_acc: 0.8821 第 3/10 纪元 235/235 [==============================] - 1s 6ms/step - loss: 0.5729 - acc: 0.8998 - val_loss: 0.6689 - val_acc: 0.8927 第 4/10 纪元 235/235 [==============================] - 1s 5ms/step - loss: 0.3911 - acc: 0.9203 - val_loss: 0.5406 - val_acc: 0.9097 第 5/10 纪元 235/235 [==============================] - 1s 6ms/step - loss: 0.3016 - acc: 0.9306 - val_loss: 0.5024 - val_acc: 0.9182 第 6/10 纪元 235/235 [==============================] - 1s 6ms/step - loss: 0.2443 - acc: 0.9405 - val_loss: 0.4571 - val_acc: 0.9242 第 7/10 纪元 235/235 [==============================] - 1s 5ms/step - loss: 0.2076 - acc: 0.9469 - val_loss: 0.4173 - val_acc: 0.9282 第 8/10 纪元 235/235 [==============================] - 1s 5ms/step - loss: 0.1852 - acc: 0.9514 - val_loss: 0.4335 - val_acc: 0.9287 第 9/10 纪元 235/235 [==============================] - 1s 6ms/step - loss: 0.1576 - acc: 0.9577 - val_loss: 0.4217 - val_acc: 0.9342 第 10/10 纪元 235/235 [==============================] - 1s 5ms/step - loss: 0.1455 - acc: 0.9597 - val_loss: 0.4151 - val_acc: 0.9344 |
这就是在 TensorFlow 模型中使用损失函数的一个示例。
进一步阅读
以下是 TensorFlow/Keras 中损失函数的一些文档
- 平均绝对误差：https://tensorflowcn.cn/api_docs/python/tf/keras/losses/MeanAbsoluteError
- 均方误差：https://tensorflowcn.cn/api_docs/python/tf/keras/losses/MeanSquaredError
- 分类交叉熵：https://tensorflowcn.cn/api_docs/python/tf/keras/losses/CategoricalCrossentropy
- 稀疏分类交叉熵：https://tensorflowcn.cn/api_docs/python/tf/keras/losses/SparseCategoricalCrossentropy
结论
在本帖中，您已经了解了损失函数以及它们在神经网络中所起的作用。您还了解了一些用于回归和分类模型的流行损失函数，以及如何在 TensorFlow 模型中使用交叉熵损失函数。
具体来说，你学到了：
- 什么是损失函数，它们与度量有何不同
- 回归和分类问题的常用损失函数
- 如何在 TensorFlow 模型中使用损失函数
谢谢，非常好。
计算中的一个错误 = \frac{1}{2}(\lvert 2-1\rvert + \lvert 3-0\rvert) = \frac{1}{2}(4) = 4 –>预期是 2
感谢您的反馈 Javad！
好的