在 PyTorch 中使用逻辑回归进行预测

作者 Muhammad Asad Iqbal Khan 于 2023年4月8日发布在 PyTorch 深度学习 2

逻辑回归是一种用于模拟事件概率的统计技术。它常用于机器学习中进行预测。当我们预测一个分类结果时，我们会应用逻辑回归。

在 PyTorch 中，逻辑回归的构建与线性回归类似。它们都应用于线性输入。但逻辑回归专门用于分类问题，例如将结果分为两种（0 或 1）。

在本教程中，我们将专注于使用逻辑回归进行预测。我们将学习 PyTorch 库中的一些有用包如何帮助轻松创建逻辑回归模型。特别是，我们将学习

如何在 PyTorch 中使用逻辑回归进行预测。
逻辑函数及其在张量上的实现。
如何使用 nn.Sequential 构建逻辑回归模型。
如何构建自定义模块用于逻辑回归。

通过我的《用PyTorch进行深度学习》一书来启动你的项目。它提供了包含可用代码的自学教程。

让我们开始吧。

在 PyTorch 中使用逻辑回归进行预测。
图片由 Manson Yim 提供。部分权利保留。

概述

本教程分为四个部分；它们是：

创建数据类
使用 nn.Module 构建模型
使用小批量梯度下降进行训练
绘制进度

什么是逻辑函数？

当使用线性函数计算数据集中某个点的类别时，我们会得到一个正数或负数，例如 -3、2、4 等。当我们构建一个分类器，特别是二分类器时，我们希望它能返回 0 或 1。在这种情况下，可以使用 sigmoid 或逻辑函数，因为该函数的值始终在 0 和 1 之间。通常我们会设置一个阈值，例如 0.5，来向上或向下取整结果，以将输出指定给一个类别或另一个类别。

在 PyTorch 中，逻辑函数由 nn.Sigmoid() 方法实现。让我们使用 PyTorch 中的 range() 方法定义一个张量，并应用逻辑函数观察输出。

import torch
torch.manual_seed(42)

xrange = torch.range(-50, 50, 0.5)
sig_func = torch.nn.Sigmoid()
y_pred = sig_func(xrange)

import torch

torch.manual_seed(42)

xrange = torch.range(-50, 50, 0.5)

sig_func = torch.nn.Sigmoid()

y_pred = sig_func(xrange)

让我们看看图表是什么样的。

import matplotlib.pyplot as plt

plt.plot(xrange.numpy(), y_pred.numpy())
plt.xlabel('range')
plt.ylabel('y_pred')
plt.show()

import matplotlib.pyplot as plt

plt.plot(xrange.numpy(), y_pred.numpy())

plt.xlabel('范围')

plt.ylabel('y_pred')

plt.show()

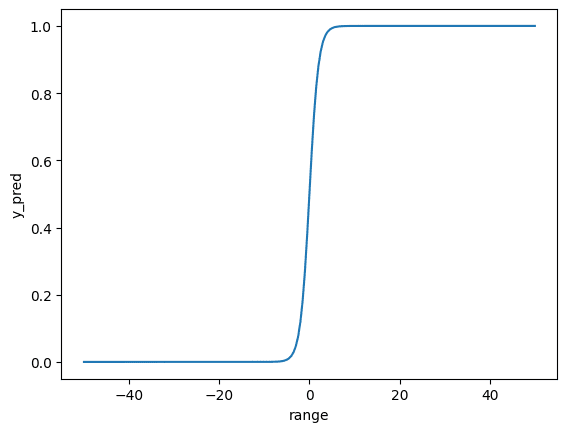
逻辑函数

正如你在图表中看到的，逻辑函数的值在 0 到 1 之间，过渡主要发生在 0 附近。

想开始使用PyTorch进行深度学习吗？

立即参加我的免费电子邮件速成课程（附示例代码）。

点击注册，同时获得该课程的免费PDF电子书版本。

通过 `nn.Sequential` 实现的逻辑回归模型

PyTorch 中的 nn.Sequential 包使我们能够像构建线性回归模型一样构建逻辑回归模型。我们只需要定义一个输入张量并通过模型进行处理。

让我们定义一个接受一维张量作为输入的逻辑回归模型对象。

...
log_regr = torch.nn.Sequential(torch.nn.Linear(1, 1), torch.nn.Sigmoid())

1 2	... log_regr = torch.nn.Sequential(torch.nn.Linear(1, 1), torch.nn.Sigmoid())

该模型包含一个线性函数层。线性函数的输出被传递到逻辑函数，该函数进行预测。

我们可以使用 parameters() 方法检查模型参数列表。在这种情况下，参数应该是随机初始化的，但我们可以看到形状与我们上面模型中指定的相匹配。

...
print(list(log_regr.parameters()))

1 2	... print(list(log_regr.parameters()))

输出看起来是这样的。

[Parameter containing:
tensor([[0.7645]], requires_grad=True), Parameter containing:
tensor([0.8300], requires_grad=True)]

[参数包含

tensor([[0.7645]], requires_grad=True), 参数包含

tensor([0.8300], requires_grad=True)]

现在，让我们定义一个一维张量 x，并使用我们的逻辑回归模型进行预测。

x = torch.tensor([[1], [2], [3], [4]], dtype=torch.float32)

1	x = torch.tensor([[1], [2], [3], [4]], dtype=torch.float32)

我们将张量强制转换为 float32 类型，因为这是我们的模型所期望的。将这些数据样本输入模型，我们将得到以下预测。

y_pred = log_regr(x)
print("here is model prediction: ", y_pred)

1 2	y_pred = log_regr(x) print("模型预测结果为： ", y_pred)

其输出如下

here is model prediction:  tensor([[0.8313],
        [0.9137],
        [0.9579],
        [0.9799]], grad_fn=<SigmoidBackward0>)

模型预测结果: tensor([[0.8313],

[0.9137],

[0.9579],

[0.9799]], grad_fn=<SigmoidBackward0>)

把所有东西放在一起，下面是完整的代码。

import matplotlib.pyplot as plt
import torch
torch.manual_seed(42)

xrange = torch.range(-50, 50, 0.5)
sig_func = torch.nn.Sigmoid()
y_pred = sig_func(xrange)
plt.plot(xrange.numpy(), y_pred.numpy())
plt.xlabel('range')
plt.ylabel('y_pred')
plt.show()

log_regr = torch.nn.Sequential(torch.nn.Linear(1, 1), torch.nn.Sigmoid())
print(list(log_regr.parameters()))

x = torch.tensor([[1], [2], [3], [4]], dtype=torch.float32)
y_pred = log_regr(x)
print("here is model prediction: ", y_pred)

import matplotlib.pyplot as plt

import torch

torch.manual_seed(42)

xrange = torch.range(-50, 50, 0.5)

sig_func = torch.nn.Sigmoid()

y_pred = sig_func(xrange)

plt.plot(xrange.numpy(), y_pred.numpy())

plt.xlabel('范围')

plt.ylabel('y_pred')

plt.show()

log_regr = torch.nn.Sequential(torch.nn.Linear(1, 1), torch.nn.Sigmoid())

print(list(log_regr.parameters()))

x = torch.tensor([[1], [2], [3], [4]], dtype=torch.float32)

y_pred = log_regr(x)

print("模型预测结果为： ", y_pred)

自定义逻辑回归模块

当您处理高级深度学习解决方案时，了解如何构建自定义模块是必要的。我们可以尝试使用语法并构建我们的自定义逻辑回归模块。这应该与上面的 nn.Sequential 模型完全相同。

我们将定义该类并继承 nn.Module 包的所有方法和属性。在类的 forward() 函数中，我们将使用 sigmoid() 方法，该方法接受来自类线性函数的输出并进行预测。

# build custom module for logistic regression
class LogisticRegression(torch.nn.Module):    
    # build the constructor
    def __init__(self, n_inputs):
        super(LogisticRegression, self).__init__()
        self.linear = torch.nn.Linear(n_inputs, 1)

    # make predictions
    def forward(self, x):
        y_pred = torch.sigmoid(self.linear(x))
        return y_pred

# 为逻辑回归构建自定义模块

class LogisticRegression(torch.nn.Module):

# 构建构造函数

def __init__(self, n_inputs):

super(LogisticRegression, self).__init__()

self.linear = torch.nn.Linear(n_inputs, 1)

# 进行预测

def forward(self, x):

y_pred = torch.sigmoid(self.linear(x))

return y_pred

我们可以实例化类对象。

...
log_regr_cus = LogisticRegression(1)

1 2	... log_regr_cus = LogisticRegression(1)

现在，让我们对上面定义的张量 x 进行预测。

...
y_pred = log_regr_cus(x)
print("here is model prediction: ", y_pred)

...

y_pred = log_regr_cus(x)

print("模型预测结果为： ", y_pred)

输出将是

here is model prediction:  tensor([[0.6647],
        [0.6107],
        [0.5537],
        [0.4954]], grad_fn=<SigmoidBackward0>)

模型预测结果: tensor([[0.6647],

[0.6107],

[0.5537],

[0.4954]], grad_fn=<SigmoidBackward0>)

正如你所见，我们的逻辑回归自定义模型与上面的 nn.Sequential 版本工作方式完全相同。

把所有东西放在一起，下面是完整的代码。

import torch
torch.manual_seed(42)

# build custom module for logistic regression
class LogisticRegression(torch.nn.Module):    
    # build the constructor
    def __init__(self, n_inputs):
        super(LogisticRegression, self).__init__()
        self.linear = torch.nn.Linear(n_inputs, 1)

    # make predictions
    def forward(self, x):
        y_pred = torch.sigmoid(self.linear(x))
        return y_pred

x = torch.tensor([[1], [2], [3], [4]], dtype=torch.float32)
log_regr_cus = LogisticRegression(1)
y_pred = log_regr_cus(x)
print("here is model prediction: ", y_pred)

import torch

torch.manual_seed(42)

# 为逻辑回归构建自定义模块

class LogisticRegression(torch.nn.Module):

# 构建构造函数

def __init__(self, n_inputs):

super(LogisticRegression, self).__init__()

self.linear = torch.nn.Linear(n_inputs, 1)

# 进行预测

def forward(self, x):

y_pred = torch.sigmoid(self.linear(x))

return y_pred

x = torch.tensor([[1], [2], [3], [4]], dtype=torch.float32)

log_regr_cus = LogisticRegression(1)

y_pred = log_regr_cus(x)

print("模型预测结果为： ", y_pred)

总结

在本教程中，您了解了逻辑回归的一些基础知识以及如何在 PyTorch 中实现它。特别是，您学习了

如何在 PyTorch 中使用逻辑回归进行预测。
关于逻辑函数及其在张量上的实现。
如何使用 nn.Sequential 构建逻辑回归模型。
如何构建自定义模块用于逻辑回归。

导航

在 PyTorch 中使用逻辑回归进行预测

概述

什么是逻辑函数？

想开始使用PyTorch进行深度学习吗？

通过 `nn.Sequential` 实现的逻辑回归模型

自定义逻辑回归模块

总结

开始使用PyTorch进行深度学习！

学习如何构建深度学习模型

通过动手练习开启你的深度学习之旅

关于此主题的更多信息

2 条对在 PyTorch 中使用逻辑回归进行预测的回复

留下回复点击此处取消回复。

导航

概述

什么是逻辑函数？

想开始使用PyTorch进行深度学习吗？

通过 nn.Sequential 实现的逻辑回归模型

自定义逻辑回归模块

总结

开始使用PyTorch进行深度学习！

学习如何构建深度学习模型

通过动手练习开启你的深度学习之旅

关于此主题的更多信息

2 条对 在 PyTorch 中使用逻辑回归进行预测 的回复

留下回复 点击此处取消回复。

通过 `nn.Sequential` 实现的逻辑回归模型

2 条对在 PyTorch 中使用逻辑回归进行预测的回复

留下回复点击此处取消回复。