
掌握时间序列预测:从 ARIMA 到 LSTM
图片来源:编辑 | Midjourney
引言
时间序列预测是一种统计技术,用于分析历史数据点并根据时间模式预测未来值。这种方法在理解趋势、季节性和周期性模式驱动关键业务决策和战略规划的领域尤为有价值。从预测股票市场波动到预测能源需求的激增,准确的时间序列分析有助于组织优化库存、高效分配资源并减轻运营风险。现代方法将传统的统计方法与机器学习相结合,以处理时间数据中的线性关系和复杂非线性模式。
在本文中,我们将探讨三种主要的预测方法
- 自回归积分滑动平均模型 (ARIMA):一种简单而流行的方法,它使用过去的值进行预测
- 指数平滑时间序列 (ETS):该方法关注随时间变化的趋势和模式,以提供更好的预测
- 长短期记忆 (LSTM):一种更先进的方法,它使用深度学习来理解复杂的数据模式
准备
首先,我们导入所需的库。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# 导入必要的库 import pandas as pd import numpy as np import matplotlib.pyplot as plt from statsmodels.tsa.arima.model import ARIMA from statsmodels.tsa.stattools import adfuller from statsmodels.tsa.holtwinters import ExponentialSmoothing from prophet import Prophet from sklearn.model_selection import train_test_split 从 sklearn.预处理 导入 MinMaxScaler from keras.models import Sequential from keras.layers import LSTM, Dense, Input |
然后,我们加载时间序列并查看其前几行。
|
1 2 3 |
# 加载你的数据集 df = pd.read_csv('timeseries.csv', parse_dates=['Date'], index_col='Date') df.head() |

1. 自回归积分滑动平均模型 (ARIMA)
ARIMA 是一个众所周知的方法,用于预测时间序列中的未来值。它结合了三个组成部分:
- 自回归 (AR):观测值与若干滞后观测值之间的关系
- 积分 (I):对原始观测值进行差分,使时间序列平稳
- 滑动平均 (MA):关系显示了观测值与使用过去数据的滑动平均模型中的预测值有何不同
我们使用增广迪基-福勒 (ADF) 检验来检查我们的数据是否随时间保持不变。我们查看此检验的 p 值。如果 p 值小于或等于 0.05,则表示我们的数据是稳定的。
|
1 2 3 4 5 6 7 8 9 10 |
# ADF 检验以检查平稳性 result = adfuller(df['Price']) print('ADF 统计量:', result[0]) print('p 值:', result[1]) if result[1] > 0.05: print("序列不平稳。需要进行差分。") else: print("序列是平稳的。") |
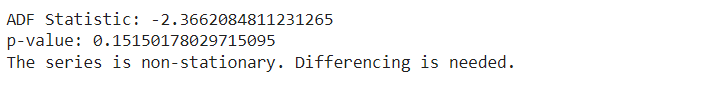
我们对时间序列数据进行一阶差分,使其平稳。
|
1 2 3 4 5 6 7 8 |
# 一阶差分 df['Differenced'] = df['Price'].diff() # 删除因差分产生的缺失值 df.dropna(inplace=True) # 显示差分数据的最后几行 print(df[['Price', 'Differenced']].head()) |

我们创建并拟合 ARIMA 模型到我们的数据。拟合模型后,我们预测未来值。
|
1 2 3 4 5 6 |
# 拟合 ARIMA 模型 model = ARIMA(df['Price'], order=(1, 1, 1)) model_fit = model.fit() # 预测后续步骤 forecast = model_fit.forecast(steps=10) |
最后,我们可视化我们的结果,以比较实际值和预测值。
|
1 2 3 4 5 6 7 8 9 |
# 绘制结果 plt.figure(figsize=(10, 5)) plt.plot(df['Price'], label='观测值') plt.plot(pd.date_range(df.index[-1], periods=10, freq='D'), forecast, label='预测值', color='red') plt.title('ARIMA 预测') plt.xlabel('日期') plt.ylabel('值') plt.legend() plt.show() |
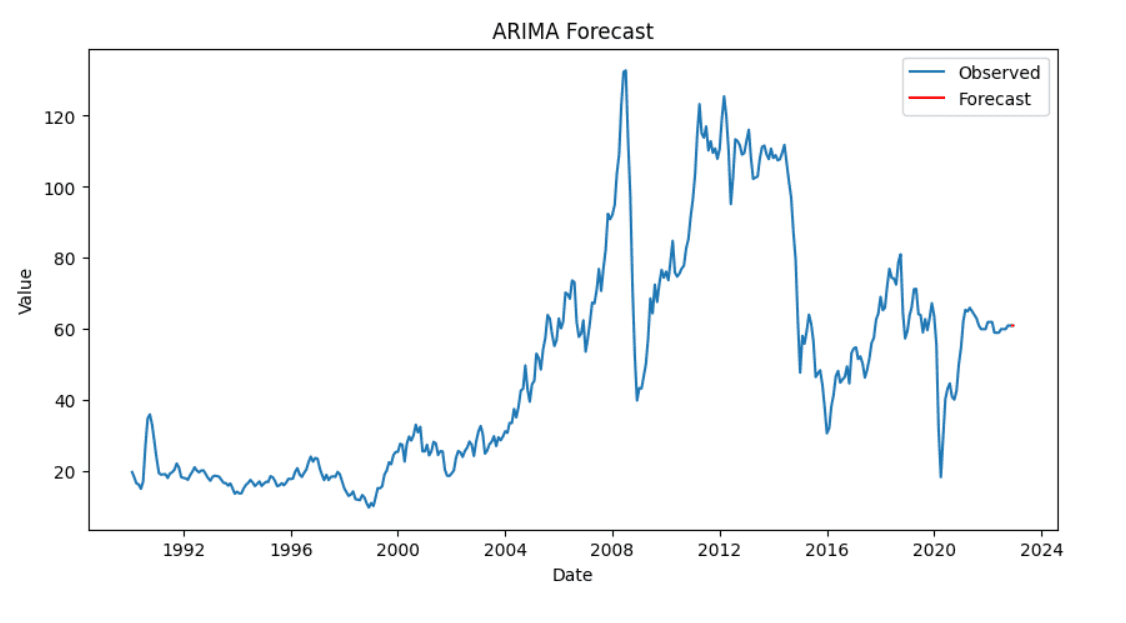
2. 指数平滑时间序列 (ETS)
指数平滑是一种用于时间序列预测的方法。它包含三个组成部分:
- 误差 (E):表示数据中的不可预测性或噪声
- 趋势 (T):显示数据的长期方向
- 季节性 (S):捕获数据中的重复模式或周期
我们将使用 Holt-Winters 方法来执行 ETS。ETS 帮助我们预测具有趋势和季节性的数据。
|
1 2 3 |
# 拟合 ETS 模型(指数平滑) ets_model = ExponentialSmoothing(df['Price'], seasonal='add', trend='add', seasonal_periods=12) ets_fit = ets_model.fit() |
我们使用拟合的 ETS 模型来生成指定数量周期的预测。
|
1 2 |
# 预测接下来的 12 个周期 forecast = ets_fit.forecast(steps=12) |
然后,我们绘制观测数据和预测值,以可视化模型的性能。
|
1 2 3 4 5 6 7 8 9 |
# 绘制观测值和预测值 plt.figure(figsize=(10, 6)) plt.plot(df, label='观测值') plt.plot(forecast, label='预测值', color='red') plt.title('ETS 模型预测') plt.xlabel('日期') plt.ylabel('价格') plt.legend() plt.show() |

3. 长短期记忆 (LSTM)
LSTM 是一种查看数据序列的神经网络。它擅长长时间记住重要细节。这使其能够用于预测时间序列数据中的未来值,因为它能够发现复杂的模式。
LSTM 对数据的尺度很敏感。因此,我们调整目标变量,确保所有值都在 0 到 1 之间。这个过程称为归一化。
|
1 2 3 4 5 6 7 8 9 10 |
# 提取目标列的值 data = df['Price'].values data = data.reshape(-1, 1) # 归一化数据 scaler = MinMaxScaler(feature_range=(0, 1)) scaled_data = scaler.fit_transform(data) # 显示前几个缩放后的值 print(scaled_data[:5]) |

LSTM 期望输入是序列的形式。在这里,我们将时间序列数据分成序列 (X) 和它们对应的下一个值 (y)。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# 创建一个函数,将数据转换为 LSTM 的序列 def create_sequences(data, time_steps=60): X, y = [], [] for i in range(len(data) - time_steps): X.append(data[i:i+time_steps, 0]) y.append(data[i+time_steps, 0]) return np.array(X), np.array(y) # 使用 60 个时间步来预测下一个值 time_steps = 60 X, y = create_sequences(scaled_data, time_steps) # 重塑 X 以供 LSTM 输入 X = X.reshape(X.shape[0], X.shape[1], 1) |
我们将数据分为训练集和测试集。
|
1 2 3 4 |
# 将数据分为训练集和测试集(80% 训练,20% 测试) train_size = int(len(X) * 0.8) X_train, X_test = X[:train_size], X[train_size:] y_train, y_test = y[:train_size], y[train_size:] |
我们将使用 Keras 构建 LSTM 模型。然后,我们将使用 Adam 优化器和均方误差损失对其进行编译。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
from keras.models import Sequential from keras.layers import LSTM, Dense, Input # 初始化 Sequential 模型 model = Sequential() # 定义输入层 model.add(Input(shape=(time_steps, 1))) # 添加 LSTM 层 model.add(LSTM(50, return_sequences=False)) # 添加一个 Dense 输出层 model.add(Dense(1)) # Compile the model model.compile(optimizer='adam', loss='mean_squared_error') |
我们使用训练数据来训练模型。我们还评估模型在测试数据上的性能。
|
1 2 |
# 在训练数据上训练模型 history = model.fit(X_train, y_train, epochs=20, batch_size=32, validation_data=(X_test, y_test)) |
训练模型后,我们将使用它来预测测试数据上的结果。
|
1 2 3 4 5 6 7 8 9 10 |
# 在测试数据上进行预测 y_pred = model.predict(X_test) # 将预测值和实际值反归一化到原始尺度 y_pred_rescaled = scaler.inverse_transform(y_pred) y_test_rescaled = scaler.inverse_transform(y_test.reshape(-1, 1)) # 显示前几个预测值和实际值 print(y_pred_rescaled[:5]) print(y_test_rescaled[:5]) |

最后,我们可以可视化预测值与实际值的对比。实际值显示为蓝色,而预测值显示为红色,并带有虚线。
|
1 2 3 4 5 6 7 8 9 |
# 绘制实际值与预测值的对比图 plt.figure(figsize=(10,6)) plt.plot(df.index[-len(y_test_rescaled):], y_test_rescaled, label='实际值', color='blue') plt.plot(df.index[-len(y_test_rescaled):], y_pred_rescaled, label='预测值', color='red', linestyle='dashed') plt.title('LSTM 时间序列预测') plt.xlabel('日期') plt.ylabel('值') plt.legend() plt.show() |
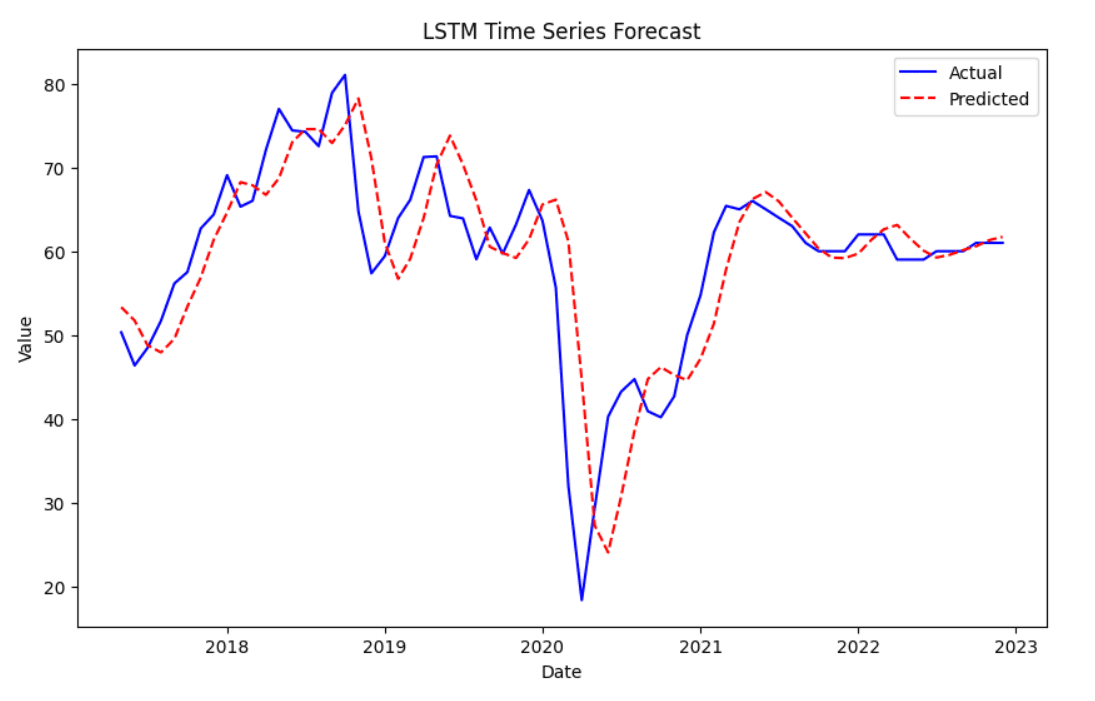
总结
在本文中,我们使用不同的方法探讨了时间序列预测。
我们从 ARIMA 模型开始。首先,我们检查数据是否平稳,然后拟合模型。
接下来,我们使用指数平滑来查找数据中的趋势和季节性。这有助于我们看到模式并做出更好的预测。
最后,我们构建了一个长短期记忆模型。该模型可以学习数据中的复杂模式。我们缩放数据,创建序列,并训练 LSTM 进行预测。
希望本指南能帮助您掌握这些时间序列预测方法。





太棒了,直奔主题。
感谢您的反馈 Francois!我们非常感激!
看起来是一篇很棒的文章,但我们中的一些人永远不会知道,因为我们无法下载数据集
并完成本文的学习。
将数据集标记为“timeseries.csv”是一个错误,因为它失去了从分析中获得真知灼见的宝贵机会,
并使结果“理论化”。