拉格朗日乘数法：支持向量机背后的理论（第1部分：线性可分情况）

本教程旨在帮助希望深入理解拉格朗日乘数法如何在构建支持向量机（SVM）模型中使用的读者。SVM最初设计用于解决二分类问题，后来扩展并应用于回归和无监督学习。它们在解决许多复杂的机器学习分类问题中取得了成功。

在本教程中，我们将探讨最简单的SVM，它假设正例和负例可以通过线性超平面完全分离。

完成本教程后，您将了解：

• 超平面如何充当决策边界
• 正例和负例的数学约束
• 什么是间隔以及如何最大化间隔
• 拉格朗日乘数法在最大化间隔中的作用
• 如何确定可分离情况下的分离超平面

让我们开始吧。

拉格朗日乘数法：支持向量机背后的理论（第一部分：可分离情况）
图片由 Mehreen Saeed 拍摄，保留部分权利。

本教程分为三个部分；它们是：

1. SVM数学模型的公式化
2. 通过拉格朗日乘数法寻找最大间隔超平面的解决方案
3. 演示所有概念的已解决示例

本教程中使用的符号

• $m$: 训练点的总数。
• $n$: 特征总数或所有数据点的维度
• $x$: 数据点，一个n维向量。
• $x^+$: 标记为+1的数据点。
• $x^-$: 标记为-1的数据点。
• $i$: 用于索引训练点的下标。$0 \leq i < m$
• $j$: 用于索引数据点单个维度的下标。$1 \leq j \leq n$
• $t$: 数据点的标签。
• T: 转置运算符。
• $w$: 权重向量，表示超平面的系数。它也是一个n维向量。
• $\alpha$: 拉格朗日乘数，每个训练点一个。这是一个m维向量。
• $d$: 数据点到决策边界的垂直距离。

作为决策边界的超平面

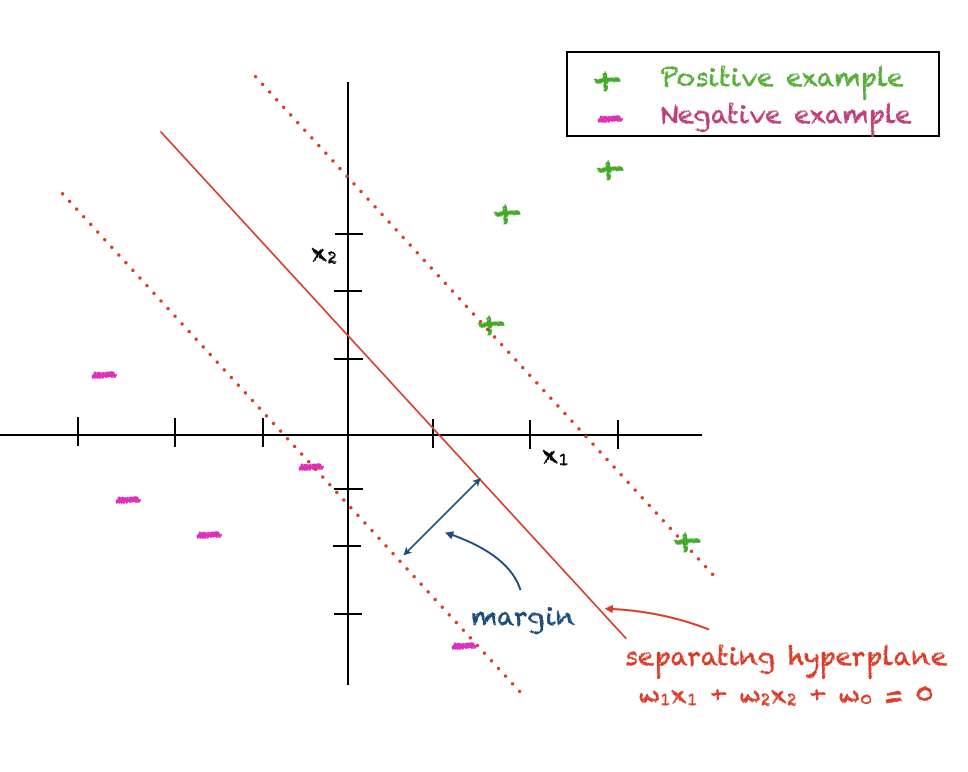
支持向量机旨在区分属于两个不同类别的数据点。一组点标记为+1，也称为正类。另一组点标记为-1，也称为负类。目前，我们做一个简化假设，即两类点可以通过线性超平面进行区分。

SVM假设两类之间存在线性决策边界，目标是找到一个能够最大化两类之间分离的超平面。因此，有时也用“最大间隔分类器”来指代SVM。最接近数据点和决策边界之间的垂直距离称为“间隔”。由于间隔完全分离了正例和负例，不容忍任何错误，因此它也称为“硬间隔”。

超平面的数学表达式如下，其中\(w_j\)是系数，\(w_0\)是确定超平面与原点距离的任意常数

$$
w^T x_i + w_0 = 0
$$

对于第i个二维点 $(x_{i1}, x_{i2})$，上述表达式简化为
$$
w_1x_{i1} + w_2 x_{i2} + w_0 = 0
$$

正例和负例的数学约束

由于我们旨在最大化正例和负例之间的间隔，我们希望正例满足以下约束

$$
w^T x_i^+ + w_0 \geq +1
$$

同样，负例应该满足

$$
w^T x_i^- + w_0 \leq -1
$$

我们可以使用一个巧妙的技巧，通过使用 $t_i \in \{-1,+1\}$ 表示数据点 $x_i$ 的类别标签，来为两组点编写一个统一的方程

$$
t_i(w^T x_i + w_0) \geq +1
$$

最大间隔超平面

数据点 $x_i$ 到间隔的垂直距离 $d_i$ 由下式给出

$$
d_i = \frac{|w^T x_i + w_0|}{||w||}
$$

为了最大化这个距离，我们可以最小化分母的平方，从而得到一个二次规划问题

$$
\min \frac{1}{2}||w||^2 \;\text{ subject to } t_i(w^Tx_i+w_0) \geq +1, \forall i
$$

通过拉格朗日乘数法求解

为了解决上述带有不等式约束的二次规划问题，我们可以使用拉格朗日乘数法。因此，拉格朗日函数为

$$
L(w, w_0, \alpha) = \frac{1}{2}||w||^2 + \sum_i \alpha_i\big(t_i(w^Tx_i+w_0) – 1\big)
$$

为了解决上述问题，我们设置以下条件

\begin{equation}
\frac{\partial L}{ \partial w} = 0, \\
\frac{\partial L}{ \partial \alpha} = 0, \\
\frac{\partial L}{ \partial w_0} = 0 \\
\end{equation}

将上述代入拉格朗日函数，得到以下优化问题，也称为对偶问题

$$
L_d = -\frac{1}{2} \sum_i \sum_k \alpha_i \alpha_k t_i t_k (x_i)^T (x_k) + \sum_i \alpha_i
$$

我们必须在以下约束下最大化上述表达式

$$
w = \sum_i \alpha_i t_i x_i
$$
和
$$
0=\sum_i \alpha_i t_i
$$

上述表达式的优点在于，我们得到了 \(w\) 关于拉格朗日乘数的表达式。目标函数中不包含 $w$ 项。每个数据点都关联一个拉格朗日乘数。$w_0$ 的计算也将在后面解释。

决定测试点的分类

任何测试点 $x$ 的分类都可以使用此表达式确定

$$
y(x) = \sum_i \alpha_i t_i x^T x_i + w_0
$$

$y(x)$ 的正值表示 $x \in +1$，负值表示 $x \in -1$

Karush-Kuhn-Tucker 条件

此外，上述带约束的优化问题满足 Karush-Kuhn-Tucker (KKT) 条件，如下所示
\begin{eqnarray}
\alpha_i &\geq& 0 \\
t_i y(x_i) -1 &\geq& 0 \\
\alpha_i(t_i y(x_i) -1) &=& 0
\end{eqnarray}

KKT条件的解释

KKT条件规定，对于每个数据点，以下之一为真

• 拉格朗日乘数为零，即 \(\alpha_i=0\)。因此，该点在分类中不起作用。

或者

• $ t_i y(x_i) = 1$ 且 $\alpha_i > 0$: 在这种情况下，数据点在决定 $w$ 的值中起作用。这样的点称为支持向量。

计算 w_0

对于 $w_0$，我们可以选择任意支持向量 $x_s$ 并求解

$$
t_s y(x_s) = 1
$$

得到
$$
t_s(\sum_i \alpha_i t_i x_s^T x_i + w_0) = 1
$$

一个已解决的例子

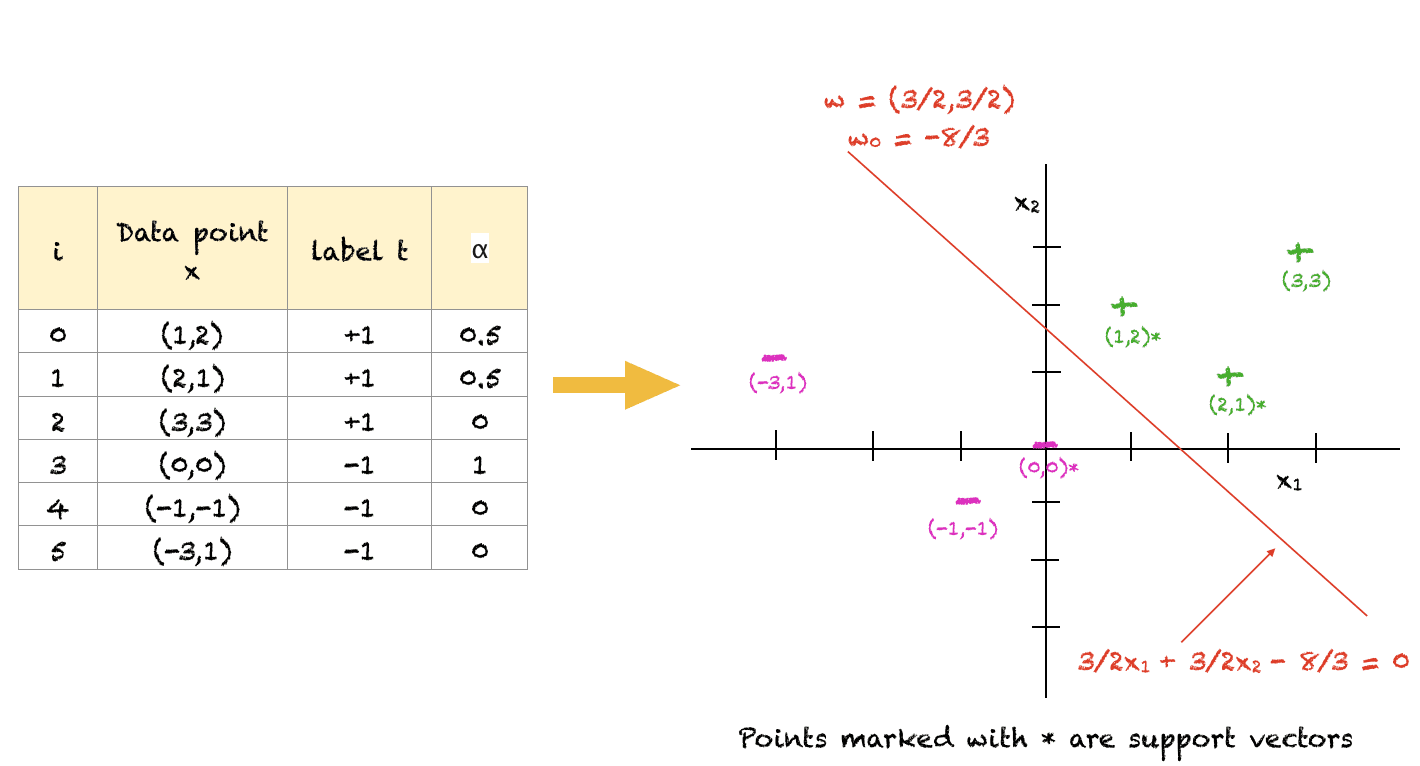
为了帮助您理解上述概念，这里有一个简单的任意解决的示例。当然，对于大量点，您将使用优化软件来解决这个问题。此外，这是一种满足所有约束的可能解决方案。目标函数可以进一步最大化，但对于最优解，超平面的斜率将保持不变。此外，对于本示例，$w_0$ 是通过对所有三个支持向量的 $w_0$ 取平均值计算的。

这个例子将向您展示模型并不像看起来那么复杂。

对于上述点集，我们可以看到(1,2)、(2,1)和(0,0)是距离分离超平面最近的点，因此作为支持向量。远离边界的点（例如(-3,1)）在决定点的分类中不起任何作用。

进一步阅读

如果您想深入了解，本节提供了更多关于该主题的资源。

书籍

• 克里斯托弗·M·毕肖普的《模式识别与机器学习》
• 《托马斯微积分》，第14版，2017年（基于乔治·B·托马斯的原始作品，由乔尔·哈斯、克里斯托弗·海尔、莫里斯·威尔修订）

文章

• 机器学习中的支持向量机
• 克里斯托弗·J·C·伯吉斯的《模式识别支持向量机教程》

总结

在本教程中，您学习了如何使用拉格朗日乘数法解决通过带有不等式约束的二次规划问题最大化间隔的问题。

具体来说，你学到了：

• 分离线性超平面的数学表达式
• 作为带有不等式约束的二次规划问题解的最大间隔
• 如何使用拉格朗日乘数法在正例和负例之间找到线性超平面

您对本文讨论的SVM有任何疑问吗？请在下面的评论中提出您的问题，我将尽力回答。

掌握机器学习微积分！

通过微积分概念变得更聪明

...通过更好地理解微积分的符号和术语

在我的新电子书中探索如何实现
机器学习微积分

它提供**自学教程**，并附有关于以下内容的**完整工作代码**：
微分、梯度、拉格朗日乘子法、雅可比矩阵等等...

将恰到好处的微积分知识带到
您的机器学习项目

查看内容