Mini-batch gradient descent 是 gradient descent 算法的一个变种,常用于训练深度学习模型。该算法的思想是将训练数据分成若干个批次(batch),然后按顺序处理这些批次。在每次迭代中,我们同时更新属于特定批次的所有训练样本的权重。这个过程会随着不同批次而重复,直到所有训练数据都被处理完毕。与 batch gradient descent 相比,这种方法的优势在于,与一次性处理所有训练样本相比,它可以显著减少计算时间和内存使用。
DataLoader 是 PyTorch 中一个用于加载和预处理深度学习模型数据的模块。它可以用于从文件加载数据,或者生成合成数据。
在本教程中,我们将向您介绍 mini-batch gradient descent 的概念。您还将了解如何使用 PyTorch 的 DataLoader 来实现它。具体来说,我们将介绍:
- 在 PyTorch 中实现 Mini-Batch Gradient Descent。
- PyTorch 中 DataLoader 的概念以及如何用它加载数据。
- Stochastic Gradient Descent 和 Mini-Batch Gradient Descent 之间的区别。
- 如何使用 PyTorch DataLoader 实现 Stochastic Gradient Descent。
- 如何使用 PyTorch DataLoader 实现 Mini-Batch Gradient Descent。
通过我的《用PyTorch进行深度学习》一书来启动你的项目。它提供了包含可用代码的自学教程。
让我们开始吧。

PyTorch 中的 Mini-Batch Gradient Descent 和 DataLoader。
图片由 Yannis Papanastasopoulos 拍摄。保留部分权利。
概述
本教程共六部分,包括:
- PyTorch 中的 DataLoader
- 准备数据和线性回归模型
- 构建数据集和 DataLoader 类
- 使用 Stochastic Gradient Descent 和 DataLoader 进行训练
- 使用 Mini-Batch Gradient Descent 和 DataLoader 进行训练
- 绘制对比图表
PyTorch 中的 DataLoader
当您计划构建深度学习管道来训练模型时,一切都始于数据加载。数据越复杂,将其加载到管道中就越困难。PyTorch 的 DataLoader 是一个方便的工具,它提供了许多选项,不仅可以轻松加载数据,还可以应用数据增强策略,并迭代处理大型数据集中的样本。您可以从 torch.utils.data 中导入 DataLoader 类,如下所示。
|
1 |
from torch.utils.data import DataLoader |
DataLoader 类中有几个参数,我们只讨论 dataset 和 batch_size。dataset 是您在 DataLoader 类中找到的第一个参数,它将数据加载到管道中。第二个参数是 batch_size,它表示每次迭代处理的训练样本数量。
|
1 |
DataLoader(dataset, batch_size=n) |
准备数据和线性回归模型
让我们重用上一教程中生成的线性回归数据。
|
1 2 3 4 5 6 7 8 9 10 |
import torch import numpy as np import matplotlib.pyplot as plt # 创建一个斜率为 -5 的函数 f(X) X = torch.arange(-5, 5, 0.1).view(-1, 1) func = -5 * X # 将高斯噪声添加到函数 f(X) 并将其保存在 Y 中 Y = func + 0.4 * torch.randn(X.size()) |
与上一教程一样,我们初始化了一个变量 X,其值范围为 -5 到 5,并创建了一个斜率为 -5 的线性函数。然后,添加高斯噪声来创建变量 Y。
我们可以使用 matplotlib 来绘制数据,以可视化模式。
|
1 2 3 4 5 6 7 8 9 |
... # 绘制并可视化蓝色数据点 plt.plot(X.numpy(), Y.numpy(), 'b+', label='Y') plt.plot(X.numpy(), func.numpy(), 'r', label='func') plt.xlabel('x') plt.ylabel('y') plt.legend() plt.grid('True', color='y') plt.show() |
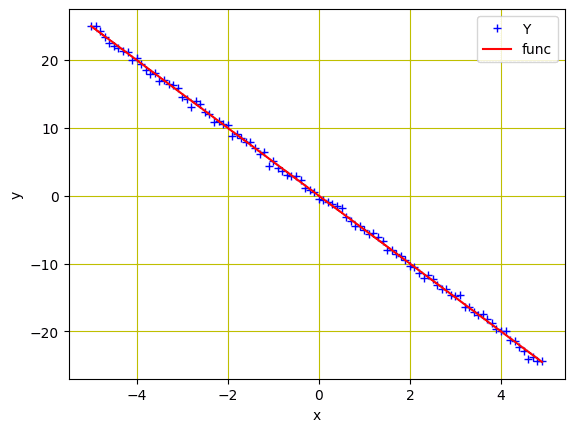
回归模型的数据点
接下来,我们将基于简单的线性回归方程构建一个前向函数。我们将训练一个具有两个参数(w 和 b)的模型。因此,让我们定义一个函数用于模型的前向传播以及一个损失函数(MSE 损失)。参数变量 w 和 b 将在函数外部定义。
|
1 2 3 4 5 6 7 8 |
... # 定义用于预测的前向传播函数 def forward(x): return w * x + b # 使用均方误差(MSE)评估数据点 def criterion(y_pred, y): return torch.mean((y_pred - y) ** 2) |
想开始使用PyTorch进行深度学习吗?
立即参加我的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
构建数据集和 DataLoader 类
让我们构建我们的 Dataset 和 DataLoader 类。Dataset 类允许我们构建自定义数据集并应用各种转换。而 DataLoader 类用于将数据集加载到管道中进行模型训练。它们创建如下。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# 创建我们的数据集类 class Build_Data(Dataset): # 构造函数 def __init__(self): self.x = torch.arange(-5, 5, 0.1).view(-1, 1) self.y = -5 * X self.len = self.x.shape[0] # 获取数据 def __getitem__(self, index): return self.x[index], self.y[index] # 获取数据长度 def __len__(self): return self.len # 创建 DataLoader 对象 dataset = Build_Data() train_loader = DataLoader(dataset = dataset, batch_size = 1) |
使用 Stochastic Gradient Descent 和 DataLoader 进行训练
当 batch_size 设置为 1 时,训练算法被称为 **stochastic gradient descent**。同样,当 batch_size 大于 1 但小于整个训练数据大小时,训练算法被称为 **mini-batch gradient descent**。为了简单起见,让我们使用 stochastic gradient descent 和 DataLoader 进行训练。
和以前一样,我们将随机初始化可训练参数 $w$ 和 $b$,定义其他参数,如学习率或步长,创建一个空列表来存储损失,并设置训练的 epoch 数。
|
1 2 3 4 5 6 |
w = torch.tensor(-10.0, requires_grad = True) b = torch.tensor(-20.0, requires_grad = True) step_size = 0.1 loss_SGD = [] n_iter = 20 |
在 SGD 中,我们只需要在每次训练迭代中从数据集中选择一个样本。因此,一个简单的 for 循环加上前向和后向传播就足够了。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
for i in range (n_iter): # 在 epoch 开始时计算损失并存储它 y_pred = forward(X) loss_SGD.append(criterion(y_pred, Y).tolist()) for x, y in train_loader: # 在前向传播中进行预测 y_hat = forward(x) # 计算原始数据点和预测数据点之间的损失 loss = criterion(y_hat, y) # 后向传播以计算损失相对于可学习参数的梯度 loss.backward() # 每次迭代后更新参数 w.data = w.data - step_size * w.grad.data b.data = b.data - step_size * b.grad.data # 每次迭代后将梯度清零 w.grad.data.zero_() b.grad.data.zero_() |
将所有内容放在一起,以下是训练模型(即 w 和 b)的完整代码。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 |
import matplotlib.pyplot as plt import torch from torch.utils.data import Dataset from torch.utils.data import DataLoader torch.manual_seed(42) # 创建一个斜率为 -5 的函数 f(X) X = torch.arange(-5, 5, 0.1).view(-1, 1) func = -5 * X # 将高斯噪声添加到函数 f(X) 并将其保存在 Y 中 Y = func + 0.4 * torch.randn(X.size()) w = torch.tensor(-10.0, requires_grad = True) b = torch.tensor(-20.0, requires_grad = True) # 定义用于预测的前向传播函数 def forward(x): return w * x + b # 使用均方误差(MSE)评估数据点 def criterion(y_pred, y): return torch.mean((y_pred - y) ** 2) # 创建我们的数据集类 class Build_Data(Dataset): # 构造函数 def __init__(self): self.x = torch.arange(-5, 5, 0.1).view(-1, 1) self.y = -5 * X self.len = self.x.shape[0] # 获取数据 def __getitem__(self, index): return self.x[index], self.y[index] # 获取数据长度 def __len__(self): return self.len # 创建 DataLoader 对象 dataset = Build_Data() train_loader = DataLoader(dataset=dataset, batch_size=1) step_size = 0.1 loss_SGD = [] n_iter = 20 for i in range (n_iter): # 在 epoch 开始时计算损失并存储它 y_pred = forward(X) loss_SGD.append(criterion(y_pred, Y).tolist()) for x, y in train_loader: # 在前向传播中进行预测 y_hat = forward(x) # 计算原始数据点和预测数据点之间的损失 loss = criterion(y_hat, y) # 后向传播以计算损失相对于可学习参数的梯度 loss.backward() # 每次迭代后更新参数 w.data = w.data - step_size * w.grad.data b.data = b.data - step_size * b.grad.data # 每次迭代后将梯度清零 w.grad.data.zero_() b.grad.data.zero_() |
使用 Mini-Batch Gradient Descent 和 DataLoader 进行训练
进一步地,我们将使用 mini-batch gradient descent 和 DataLoader 来训练我们的模型。我们将为训练设置不同的 batch_size,即 batch_size 为 10 和 20。batch_size 为 10 的训练如下:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
... train_loader_10 = DataLoader(dataset=dataset, batch_size=10) w = torch.tensor(-10.0, requires_grad=True) b = torch.tensor(-20.0, requires_grad=True) step_size = 0.1 loss_MBGD_10 = [] iter = 20 for i in range (iter): # 在 epoch 开始时计算损失并存储它 y_pred = forward(X) loss_MBGD_10.append(criterion(y_pred, Y).tolist()) for x, y in train_loader_10: # 在前向传播中进行预测 y_hat = forward(x) # 计算原始数据点和预测数据点之间的损失 loss = criterion(y_hat, y) # 后向传播以计算损失相对于可学习参数的梯度 loss.backward() # 每次迭代后更新参数 w.data = w.data - step_size * w.grad.data b.data = b.data - step_size * b.grad.data # 每次迭代后将梯度清零 w.grad.data.zero_() b.grad.data.zero_() |
我们如何用 batch_size 为 20 来实现同样的功能:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
... train_loader_20 = DataLoader(dataset=dataset, batch_size=20) w = torch.tensor(-10.0, requires_grad=True) b = torch.tensor(-20.0, requires_grad=True) step_size = 0.1 loss_MBGD_20 = [] iter = 20 for i in range(iter): # 在 epoch 开始时计算损失并存储它 y_pred = forward(X) loss_MBGD_20.append(criterion(y_pred, Y).tolist()) for x, y in train_loader_20: # 在前向传播中进行预测 y_hat = forward(x) # 计算原始数据点和预测数据点之间的损失 loss = criterion(y_hat, y) # 后向传播以计算损失相对于可学习参数的梯度 loss.backward() # 每次迭代后更新参数 w.data = w.data - step_size * w.grad.data b.data = b.data - step_size * b.grad.data # 每次迭代后将梯度清零 w.grad.data.zero_() b.grad.data.zero_() |
将所有内容放在一起,完整代码如下:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 |
import matplotlib.pyplot as plt import torch from torch.utils.data import Dataset from torch.utils.data import DataLoader torch.manual_seed(42) # 创建一个斜率为 -5 的函数 f(X) X = torch.arange(-5, 5, 0.1).view(-1, 1) func = -5 * X # 将高斯噪声添加到函数 f(X) 并将其保存在 Y 中 Y = func + 0.4 * torch.randn(X.size()) w = torch.tensor(-10.0, requires_grad=True) b = torch.tensor(-20.0, requires_grad=True) # 定义用于预测的前向传播函数 def forward(x): return w * x + b # 使用均方误差(MSE)评估数据点 def criterion(y_pred, y): return torch.mean((y_pred - y) ** 2) # 创建我们的数据集类 class Build_Data(Dataset): # 构造函数 def __init__(self): self.x = torch.arange(-5, 5, 0.1).view(-1, 1) self.y = -5 * X self.len = self.x.shape[0] # 获取数据 def __getitem__(self, index): return self.x[index], self.y[index] # 获取数据长度 def __len__(self): return self.len # 创建 DataLoader 对象 dataset = Build_Data() train_loader_10 = DataLoader(dataset=dataset, batch_size=10) step_size = 0.1 loss_MBGD_10 = [] iter = 20 for i in range(n_iter): # 在 epoch 开始时计算损失并存储它 y_pred = forward(X) loss_MBGD_10.append(criterion(y_pred, Y).tolist()) for x, y in train_loader_10: # 在前向传播中进行预测 y_hat = forward(x) # 计算原始数据点和预测数据点之间的损失 loss = criterion(y_hat, y) # 后向传播以计算损失相对于可学习参数的梯度 loss.backward() # 每次迭代后更新参数 w.data = w.data - step_size * w.grad.data b.data = b.data - step_size * b.grad.data # 每次迭代后将梯度清零 w.grad.data.zero_() b.grad.data.zero_() train_loader_20 = DataLoader(dataset=dataset, batch_size=20) # 重置 w 和 b w = torch.tensor(-10.0, requires_grad=True) b = torch.tensor(-20.0, requires_grad=True) loss_MBGD_20 = [] for i in range(n_iter): # 在 epoch 开始时计算损失并存储它 y_pred = forward(X) loss_MBGD_20.append(criterion(y_pred, Y).tolist()) for x, y in train_loader_20: # 在前向传播中进行预测 y_hat = forward(x) # 计算原始数据点和预测数据点之间的损失 loss = criterion(y_hat, y) # 后向传播以计算损失相对于可学习参数的梯度 loss.backward() # 每次迭代后更新参数 w.data = w.data - step_size * w.grad.data b.data = b.data - step_size * b.grad.data # 每次迭代后将梯度清零 w.grad.data.zero_() b.grad.data.zero_() |
绘制对比图表
最后,让我们可视化在训练过程中,三种算法(即 stochastic gradient descent、batch_size 为 10 的 mini-batch gradient descent 和 batch_size 为 20 的 mini-batch gradient descent)的损失如何下降。
|
1 2 3 4 5 6 7 |
plt.plot(loss_SGD,label = "Stochastic Gradient Descent") plt.plot(loss_MBGD_10,label = "Mini-Batch-10 Gradient Descent") plt.plot(loss_MBGD_20,label = "Mini-Batch-20 Gradient Descent") plt.xlabel('epoch') plt.ylabel('Cost/total loss') plt.legend() plt.show() |
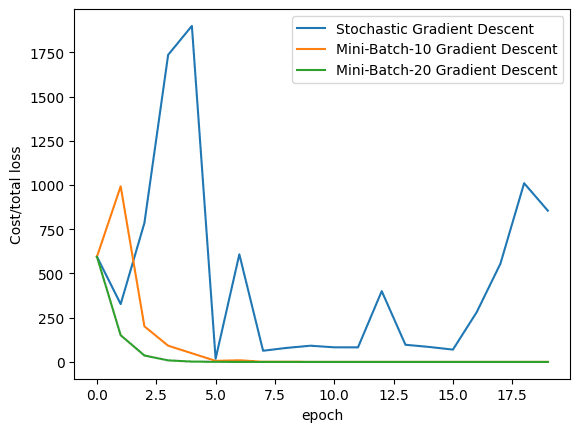
从图中可以看出,mini-batch gradient descent 可以更快地收敛,因为我们可以通过在每一步计算平均损失来更精确地更新参数。
将所有内容放在一起,完整代码如下:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 |
import matplotlib.pyplot as plt import torch from torch.utils.data import Dataset from torch.utils.data import DataLoader torch.manual_seed(42) # 创建一个斜率为 -5 的函数 f(X) X = torch.arange(-5, 5, 0.1).view(-1, 1) func = -5 * X # 将高斯噪声添加到函数 f(X) 并将其保存在 Y 中 Y = func + 0.4 * torch.randn(X.size()) w = torch.tensor(-10.0, requires_grad=True) b = torch.tensor(-20.0, requires_grad=True) # 定义用于预测的前向传播函数 def forward(x): return w * x + b # 使用均方误差(MSE)评估数据点 def criterion(y_pred, y): return torch.mean((y_pred - y) ** 2) # 创建我们的数据集类 class Build_Data(Dataset): # 构造函数 def __init__(self): self.x = torch.arange(-5, 5, 0.1).view(-1, 1) self.y = -5 * X self.len = self.x.shape[0] # 获取数据 def __getitem__(self, index): return self.x[index], self.y[index] # 获取数据长度 def __len__(self): return self.len # 创建 DataLoader 对象 dataset = Build_Data() train_loader = DataLoader(dataset=dataset, batch_size=1) step_size = 0.1 loss_SGD = [] n_iter = 20 for i in range(n_iter): # 在 epoch 开始时计算损失并存储它 y_pred = forward(X) loss_SGD.append(criterion(y_pred, Y).tolist()) for x, y in train_loader: # 在前向传播中进行预测 y_hat = forward(x) # 计算原始数据点和预测数据点之间的损失 loss = criterion(y_hat, y) # 后向传播以计算损失相对于可学习参数的梯度 loss.backward() # 每次迭代后更新参数 w.data = w.data - step_size * w.grad.data b.data = b.data - step_size * b.grad.data # 每次迭代后将梯度清零 w.grad.data.zero_() b.grad.data.zero_() train_loader_10 = DataLoader(dataset=dataset, batch_size=10) # 重置 w 和 b w = torch.tensor(-10.0, requires_grad=True) b = torch.tensor(-20.0, requires_grad=True) loss_MBGD_10 = [] for i in range(n_iter): # 在 epoch 开始时计算损失并存储它 y_pred = forward(X) loss_MBGD_10.append(criterion(y_pred, Y).tolist()) for x, y in train_loader_10: # 在前向传播中进行预测 y_hat = forward(x) # 计算原始数据点和预测数据点之间的损失 loss = criterion(y_hat, y) # 后向传播以计算损失相对于可学习参数的梯度 loss.backward() # 每次迭代后更新参数 w.data = w.data - step_size * w.grad.data b.data = b.data - step_size * b.grad.data # 每次迭代后将梯度清零 w.grad.data.zero_() b.grad.data.zero_() train_loader_20 = DataLoader(dataset=dataset, batch_size=20) # 重置 w 和 b w = torch.tensor(-10.0, requires_grad=True) b = torch.tensor(-20.0, requires_grad=True) loss_MBGD_20 = [] for i in range(n_iter): # 在 epoch 开始时计算损失并存储它 y_pred = forward(X) loss_MBGD_20.append(criterion(y_pred, Y).tolist()) for x, y in train_loader_20: # 在前向传播中进行预测 y_hat = forward(x) # 计算原始数据点和预测数据点之间的损失 loss = criterion(y_hat, y) # 后向传播以计算损失相对于可学习参数的梯度 loss.backward() # 每次迭代后更新参数 w.data = w.data - step_size * w.grad.data b.data = b.data - step_size * b.grad.data # 每次迭代后将梯度清零 w.grad.data.zero_() b.grad.data.zero_() plt.plot(loss_SGD,label="Stochastic Gradient Descent") plt.plot(loss_MBGD_10,label="Mini-Batch-10 Gradient Descent") plt.plot(loss_MBGD_20,label="Mini-Batch-20 Gradient Descent") plt.xlabel('epoch') plt.ylabel('Cost/total loss') plt.legend() plt.show() |
总结
在本教程中,您了解了 mini-batch gradient descent、DataLoader 以及它们在 PyTorch 中的实现。特别是,您学到了:
- 在 PyTorch 中实现 mini-batch gradient descent。
- PyTorch 中
DataLoader的概念以及如何用它加载数据。 - stochastic gradient descent 和 mini-batch gradient descent 之间的区别。
- 如何使用 PyTorch
DataLoader实现 stochastic gradient descent。 - 如何使用 PyTorch
DataLoader实现 mini-batch gradient descent。







暂无评论。