Transformer 模型在许多 NLP 任务中被证明非常有效。虽然通过增加维度和层数可以增强其能力,但这也会显著增加计算复杂度。专家混合 (MoE) 架构通过引入稀疏性提供了一个优雅的解决方案,使得模型能够高效地扩展,而不会成比例地增加计算成本。
在这篇文章中,您将学习 Transformer 模型中的专家混合架构。具体来说,您将学习:
- 为什么需要 MoE 架构才能高效地扩展 Transformer
- MoE 的工作原理及其关键组件
- 如何在 Transformer 模型中实现 MoE
让我们开始吧。

Transformer 模型中的混合专家(Mixture of Experts)架构
图片来源:realfish。保留部分权利。
概述
这篇文章涵盖了三个主要领域:
- 为什么 Transformer 中需要专家混合
- 专家混合的工作原理
- Transformer 模型中 MoE 的实现
为什么 Transformer 中需要专家混合
专家混合 (MoE) 概念于 1991 年由 Jacobs 等人首次提出。它使用多个“专家”模型来处理输入,并通过“门”机制选择使用哪个专家。MoE 随着 2021 年的 Switch Transformer 和 2024 年的 Mixtral 模型而重新受到关注。在 Transformer 模型中,MoE 只为每个输入激活一部分参数,从而允许定义大型模型,同时每次计算只使用一部分。
考虑 Mixtral 模型架构:
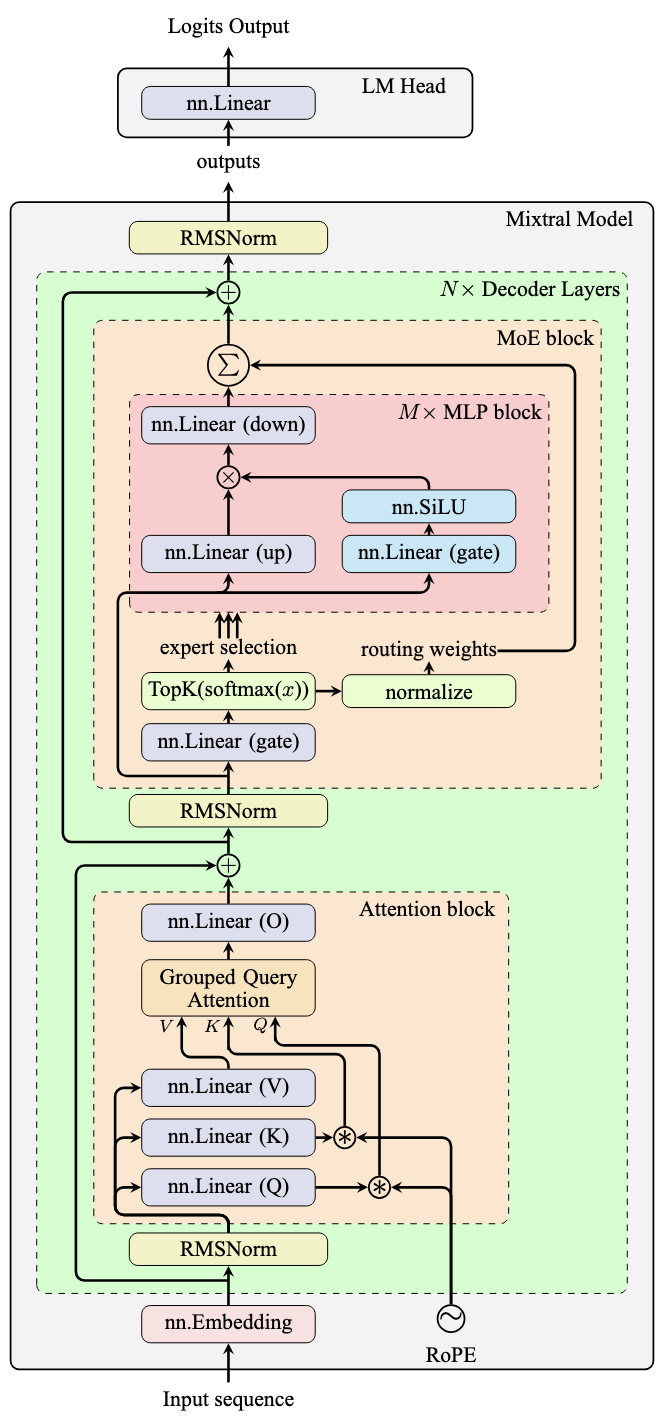
Mixtral 模型架构
如上一篇文章所述,MLP 块为 Transformer 层引入了非线性。注意力块仅使用线性组合对输入序列的信息进行混洗。Transformer 模型的“智能”主要存在于 MLP 块中。
这解释了为什么 MLP 块通常包含 Transformer 模型中大部分参数和计算负载。训练 MLP 块在各种任务中表现良好具有挑战性,因为不同的任务可能需要相互矛盾的行为。
一个解决方案是为每个任务创建专门的模型,并使用路由器选择合适的模型。或者,您可以将多个模型和路由器组合到一个模型中并一起训练。这就是 MoE 的本质。
MoE 通过拥有多个专家,并且每次只激活稀疏子集来引入稀疏性。MoE 架构只修改 MLP 块,而所有专家共享相同的注意力块。每个 Transformer 层都有一组独立的专家,从而可以在层之间进行混合搭配组合。这允许创建许多专家,而不会大幅增加参数数量,从而在保持计算成本低的情况下扩展模型。
关键的洞察是,不同的输入受益于不同的专业计算。通过拥有多个专家网络和路由机制来选择要使用的专家,模型以更少的计算资源实现了更好的性能。
专家混合的工作原理
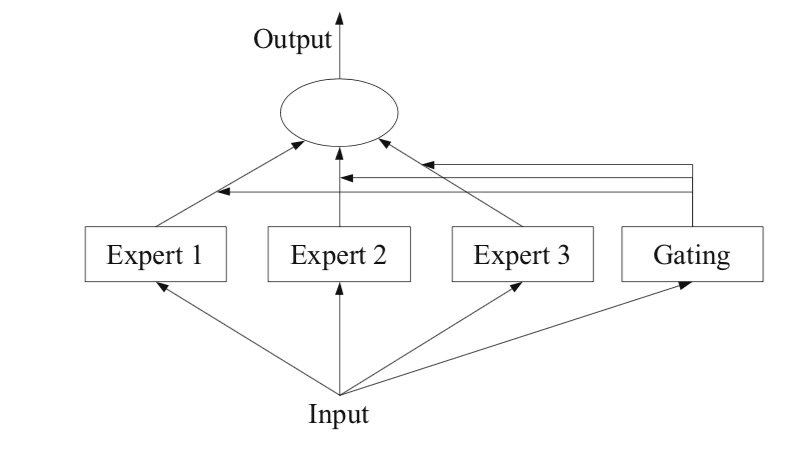
MoE 架构由三个关键组件组成:
- 专家网络:多个独立的神经网络(专家),用于处理输入,类似于其他 Transformer 模型中的 MLP 块。
- 路由器:决定哪些专家应该处理每个输入的机制。通常是一个线性层,后跟 softmax,产生一个关于 $N$ 个专家的概率分布。路由器输出通过“门控机制”选择 top-$k$ 专家。
- 输出组合:top-$k$ 专家处理输入,它们的输出使用路由器归一化的概率作为加权和进行组合。
基本的 MoE 操作如下。对于来自注意力块输出序列的每个向量 $x$,路由器将其与一个矩阵相乘以产生 logits(上图中的门层)。在 softmax 变换之后,这些 logits 通过 top-$k$ 操作进行过滤,产生 $k$ 个索引和 $k$ 个概率。索引激活专家(图中的 MLP 块),它们处理原始注意力块输出。专家输出使用归一化的路由器概率作为加权和进行组合。
概念上,MoE 块计算:
$$
\text{MoE}(x) = \sum_{i \in \text{TopK}(p)} p_i \cdot \text{Expert}_i(x)
$$
$k$ 的值是模型超参数。即使 $k=2$ 也被发现足以获得良好的性能。
Transformer 模型中 MoE 的实现
以下是 PyTorch 中一个 Transformer 层的实现,其中 MoE 替换了传统的 MLP 块:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 |
import torch import torch.nn as nn import torch.nn.functional as F class Expert(nn.Module): def __init__(self, dim, intermediate_dim): super().__init__() self.gate_proj = nn.Linear(dim, intermediate_dim) self.up_proj = nn.Linear(dim, intermediate_dim) self.down_proj = nn.Linear(intermediate_dim, dim) self.act = nn.SiLU() def forward(self, x): gate = self.gate_proj(x) up = self.up_proj(x) swish = self.act(gate) output = self.down_proj(swish * up) return output class MoELayer(nn.Module): def __init__(self, dim, intermediate_dim, num_experts, top_k=2): super().__init__() self.num_experts = num_experts self.top_k = top_k self.dim = dim # 创建专家网络 self.experts = nn.ModuleList([ Expert(dim, intermediate_dim) for _ in range(num_experts) ]) self.router = nn.Linear(dim, num_experts) def forward(self, hidden_states): batch_size, seq_len, hidden_dim = hidden_states.shape # 重塑以进行专家处理,计算路由概率 hidden_states_reshaped = hidden_states.view(-1, hidden_dim) router_logits = self.router(hidden_states_reshaped) # (batch_size * seq_len, num_experts) routing_probs = F.softmax(router_logits, dim=-1) # 选择 top-k 专家,并按比例缩放概率使其和为 1 # 输出形状:(batch_size * seq_len, k) top_k_probs, top_k_indices = torch.topk(routing_probs, self.top_k, dim=-1) top_k_probs = top_k_probs / top_k_probs.sum(dim=-1, keepdim=True) # 通过选定的专家进行处理 output = [] for i in range(self.top_k): expert_idx = top_k_indices[:, i] expert_probs = top_k_probs[:, i] # 使用选定的专家处理批次和序列中的每个向量 expert_output = torch.stack([ self.experts[exp_idx](hidden_states_reshaped[j]) for j, exp_idx in enumerate(expert_idx) ], dim=0) # 按路由概率加权求和 output.append(expert_probs.unsqueeze(-1) * expert_output) # 重塑回原始形状 output = sum(output).view(batch_size, seq_len, hidden_dim) return output class MoETransformerLayer(nn.Module): def __init__(self, dim, intermediate_dim, num_experts, top_k=2, num_heads=8): super().__init__() self.attention = nn.MultiheadAttention(dim, num_heads, batch_first=True) self.moe = MoELayer(dim, intermediate_dim, num_experts, top_k) self.norm1 = nn.RMSNorm(dim) self.norm2 = nn.RMSNorm(dim) def forward(self, x): # 注意力子层 input_x = x x = self.norm1(x) attn_output, _ = self.attention(x, x, x) input_x = input_x + attn_output # MoE 子层 x = self.norm2(input_x) moe_output = self.moe(x) return input_x + moe_output |
一个完整的 MoE Transformer 模型由一系列 Transformer 层组成。每个层包含一个注意力子层和一个 MoE 子层,其中 MoE 子层像其他 Transformer 模型中的 MLP 子层一样运行。
在 MoELayer 类中,forward() 方法期望输入形状为 (batch_size, seq_len, hidden_dim)。由于每个序列向量都是独立处理的,因此输入首先被重塑为 (batch_size * seq_len, hidden_dim)。路由器和 softmax 函数生成形状为 (batch_size * seq_len, num_experts) 的 routing_probs,指示每个专家对输出的贡献。
top-$k$ 操作选择专家及其相应的概率。在 for 循环中,每个向量由一个专家处理,并将输出堆叠在一起。循环生成一个缩放张量 output 列表,它们被求和以获得最终输出。然后将此输出重塑回原始的 (batch_size, seq_len, hidden_dim) 形状。
Expert 类与上一篇文章中的 MLP 块相同,但 MoE 子层使用多个实例,而不是 Transformer 层。
您可以使用此代码测试 Transformer 层:
|
1 2 3 4 5 6 7 8 9 |
batch_size = 4 seq_len = 10 dim = 16 intermediate_dim = 72 num_experts = 8 x = torch.randn(batch_size, seq_len, dim) model = MoETransformerLayer(dim, intermediate_dim, num_experts) y = model(x) |
共享专家
上述实现是最简单的 MoE。最近,DeepSeek 模型提出并推广了一种新思想,即在 MoE 架构中包含几个“共享专家”,以便这些共享专家始终用于任何输入。数学上,这使得 MoE 计算为:
$$
\text{MoE}(x) = \text{Expert}^\ast(x) + \sum_{i \in \text{TopK}(p)} p_i \cdot \text{Expert}_i(x)
$$
额外添加的专家是共享专家。显然,您可以使用多个共享专家。在所有情况下,共享专家都不需要路由器,而是无条件地接受输入。
要实现共享专家,您可以重用上述代码并在 MoeTransformerLayer 类中添加额外的专家:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
class MoETransformerLayer(nn.Module): def __init__(self, dim, intermediate_dim, num_experts, top_k=2, num_heads=8, num_shared_experts=1): super().__init__() self.attention = nn.MultiheadAttention(dim, num_heads, batch_first=True) self.moe = MoELayer(dim, intermediate_dim, num_experts, top_k) # 共享专家 self.shared_experts = nn.ModuleList([ Expert(dim, intermediate_dim) for _ in range(num_shared_experts) ]) self.norm1 = nn.RMSNorm(dim) self.norm2 = nn.RMSNorm(dim) def forward(self, x): # 注意力子层 input_x = x x = self.norm1(x) attn_output, _ = self.attention(x, x, x) input_x = input_x + attn_output # MoE 子层 x = self.norm2(input_x) moe_output = self.moe(x) for expert in self.shared_experts: moe_output += expert(x) return input_x + moe_output |
进一步阅读
以下是一些您可能会觉得有用的资源:
- 什么是专家混合?
- 局部专家的自适应混合
- Switch Transformers:通过简单高效的稀疏性扩展到万亿参数模型
- 专家 Mixtral
- 惊人大型神经网络:稀疏门控专家混合层
- GLaM:利用专家混合高效扩展语言模型
- 具有专家选择路由的专家混合
- DeepSeekMoE:迈向专家混合语言模型中的终极专家专业化
总结
在这篇文章中,您了解了 Transformer 模型中的专家混合架构。具体来说,您学习了:
- 为什么需要 MoE 才能高效扩展 Transformer 模型
- MoE 如何与专家模型、路由器和门控机制协同工作
- 如何在 Transformer 模型中实现可替代传统 MLP 层的 MoE 层




嗨,Adrian!代码中仍然缺少位置编码。
嗨,Wilfredo……请提供更多关于您所遇到的问题的详细信息。