深度学习神经网络模型是高度灵活的非线性算法,能够学习几乎无限数量的映射函数。
这种灵活性带来的一个令人沮丧的问题是最终模型的高方差。在相同数据集上训练的相同神经网络模型,每次运行时都可能找到许多不同“足够好”的解决方案之一。
模型平均是一种集成学习技术,它通过牺牲模型性能的扩展性来减少最终神经网络模型的方差,以获得对模型预期性能的信心。
在本教程中,您将学习如何在 Keras 中开发模型平均集成,以减少最终模型的方差。
完成本教程后,您将了解:
- 模型平均是一种集成学习技术,可用于减少深度学习神经网络模型的预期方差。
- 如何在 Keras 中实现分类和回归预测建模问题的模型平均。
- 如何解决多类分类问题,并使用模型平均来减少最终模型的方差。
用我的新书《更好的深度学习》来启动你的项目,书中包含分步教程和所有示例的 Python 源代码文件。
让我们开始吧。
- 2019 年 10 月更新:更新至 Keras 2.3 和 TensorFlow 2.0。
- 2020年1月更新:已针对 scikit-learn v0.22 API 的更改进行更新。

如何在 Keras 中使用模型平均集成来减少深度学习模型的方差
照片由 John Mason 拍摄,保留部分权利。
教程概述
本教程分为六个部分;它们是:
- 模型平均
- 如何在 Keras 中平均模型
- 多类别分类问题
- 用于多类分类的 MLP 模型
- MLP 模型的高方差
- 模型平均集成
模型平均
深度学习神经网络模型是通过随机训练算法学习的非线性方法。
这意味着它们具有高度灵活性,能够学习变量之间复杂的关联,并在资源充足的情况下近似任何映射函数。这种灵活性的一个缺点是模型具有高方差。
这意味着模型高度依赖于用于训练模型的特定训练数据、初始条件(随机初始权重)以及训练过程中的偶然性。结果是,每次在相同数据集上训练相同模型配置时,最终模型都会做出不同的预测。
当训练一个最终模型用于对新数据进行预测时,例如在操作中或机器学习竞赛中,这可能会令人沮丧。
可以通过为问题训练多个模型并组合它们的预测来解决该方法的高方差问题。这种方法称为模型平均,属于集成学习技术家族。
想要通过深度学习获得更好的结果吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
如何在 Keras 中平均模型
在 Keras 中开发模型平均集成的最简单方法是在相同数据集上训练多个模型,然后组合每个训练模型的预测。
训练多个模型
根据模型的大小和训练数据的大小,训练多个模型可能需要大量的资源。
您可能需要在相同的硬件上顺序训练模型。对于非常大的模型,可能值得使用云基础设施(例如Amazon Web Services)并行训练模型。
集成所需的模型数量可能因问题的复杂性和模型而异。该方法的一个优点是您可以继续创建模型,将它们添加到集成中,并通过对保留测试集进行预测来评估它们对性能的影响。
对于小型模型,您可以按顺序训练模型并将其保存在内存中以供实验使用。例如
|
1 2 3 4 5 6 7 8 9 10 |
... # 训练模型并将其保存在内存中 n_members = 10 models = list() for _ in range(n_members): # 定义和拟合模型 model = ... # 将模型作为集成成员存储在内存中 models.add(models) ... |
对于大型模型,可能在不同的硬件上训练,您可以将每个模型保存到文件。
|
1 2 3 4 5 6 7 8 9 10 11 |
... # 训练模型并将其保存到文件 n_members = 10 for i in range(n_members): # 定义和拟合模型 model = ... # 将模型保存到文件 filename = 'model_' + str(i + 1) + '.h5' model.save(filename) print('Saved: %s' % filename) ... |
模型稍后可以加载。
小型模型可以全部同时加载到内存中,而非常大型的模型可能必须一次加载一个以进行预测,然后将预测结果合并。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
from keras.models import load_model ... # 加载预训练的集成成员 n_members = 10 models = list() for i in range(n_members): # 加载模型 filename = 'model_' + str(i + 1) + '.h5' model = load_model(filename) # 存储在内存中 models.append(model) ... |
合并预测
模型准备好后,每个模型都可以用于进行预测,并且可以将预测结果合并。
在每个模型都预测实数值输出的回归问题中,可以收集这些值并计算平均值。
|
1 2 3 4 5 6 |
... # 进行预测 yhats = [model.predict(testX) for model in models] yhats = array(yhats) # 计算平均值 outcomes = mean(yhats) |
在分类问题中,有两种选择。
第一种是计算预测整数类别值的众数。
|
1 2 3 4 5 6 |
... # 进行预测 yhats = [model.predict_classes(testX) for model in models] yhats = array(yhats) # 计算众数 outcomes, _ = mode(yhats) |
这种方法的一个缺点是,对于小型集成或具有大量类别的问题,预测样本可能不够大,无法使众数具有意义。
在二元分类问题中,输出层使用 sigmoid 激活函数,预测概率的平均值可以像回归问题一样计算。
在具有两个以上类别的多类分类问题中,输出层使用 softmax 激活函数,可以计算每个预测类别的概率之和,然后再取argmax以获得类别值。
|
1 2 3 4 5 6 7 8 |
... # 进行预测 yhats = [model.predict(testX) for model in models] yhats = array(yhats) # 在集成中求和 summed = numpy.sum(yhats, axis=0) # 对类别求argmax outcomes = argmax(summed, axis=1) |
这些组合 Keras 模型预测的方法同样适用于多层感知器、卷积神经网络和循环神经网络。
既然我们知道如何在 Keras 中对多个神经网络模型的预测进行平均,那么我们来研究一个案例。
多类别分类问题
我们将使用一个小型多类分类问题作为基础来演示模型平均集成。
scikit-learn 类提供了 make_blobs() 函数,可用于创建具有规定样本数、输入变量、类别和类别内样本方差的多类分类问题。
我们使用这个包含 500 个示例的问题,其中输入变量(表示点的 x 和 y 坐标)和每个组内点的标准差为 2.0。我们将使用相同的随机状态(伪随机数生成器的种子)以确保我们始终获得相同的 500 个点。
|
1 2 |
# 生成二维分类数据集 X, y = make_blobs(n_samples=500, centers=3, n_features=2, cluster_std=2, random_state=2) |
结果是我们可以建模的数据集的输入和输出元素。
为了了解问题的复杂性,我们可以将每个点绘制在二维散点图上,并按类别值对每个点进行着色。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# blob 数据集的散点图 from sklearn.datasets import make_blobs from matplotlib import pyplot from pandas import DataFrame # 生成二维分类数据集 X, y = make_blobs(n_samples=500, centers=3, n_features=2, cluster_std=2, random_state=2) # 散点图,点按类别值着色 df = DataFrame(dict(x=X[:,0], y=X[:,1], label=y)) colors = {0:'red', 1:'blue', 2:'green'} fig, ax = pyplot.subplots() grouped = df.groupby('label') for key, group in grouped: group.plot(ax=ax, kind='scatter', x='x', y='y', label=key, color=colors[key]) pyplot.show() |
运行此示例将生成整个数据集的散点图。我们可以看到,标准差为 2.0 意味着这些类不是线性可分的(不能用一条线分开),导致许多模糊的点。
这是可取的,因为它意味着问题不是微不足道的,并且将允许神经网络模型找到许多不同的“足够好”的候选解决方案,从而导致高方差。
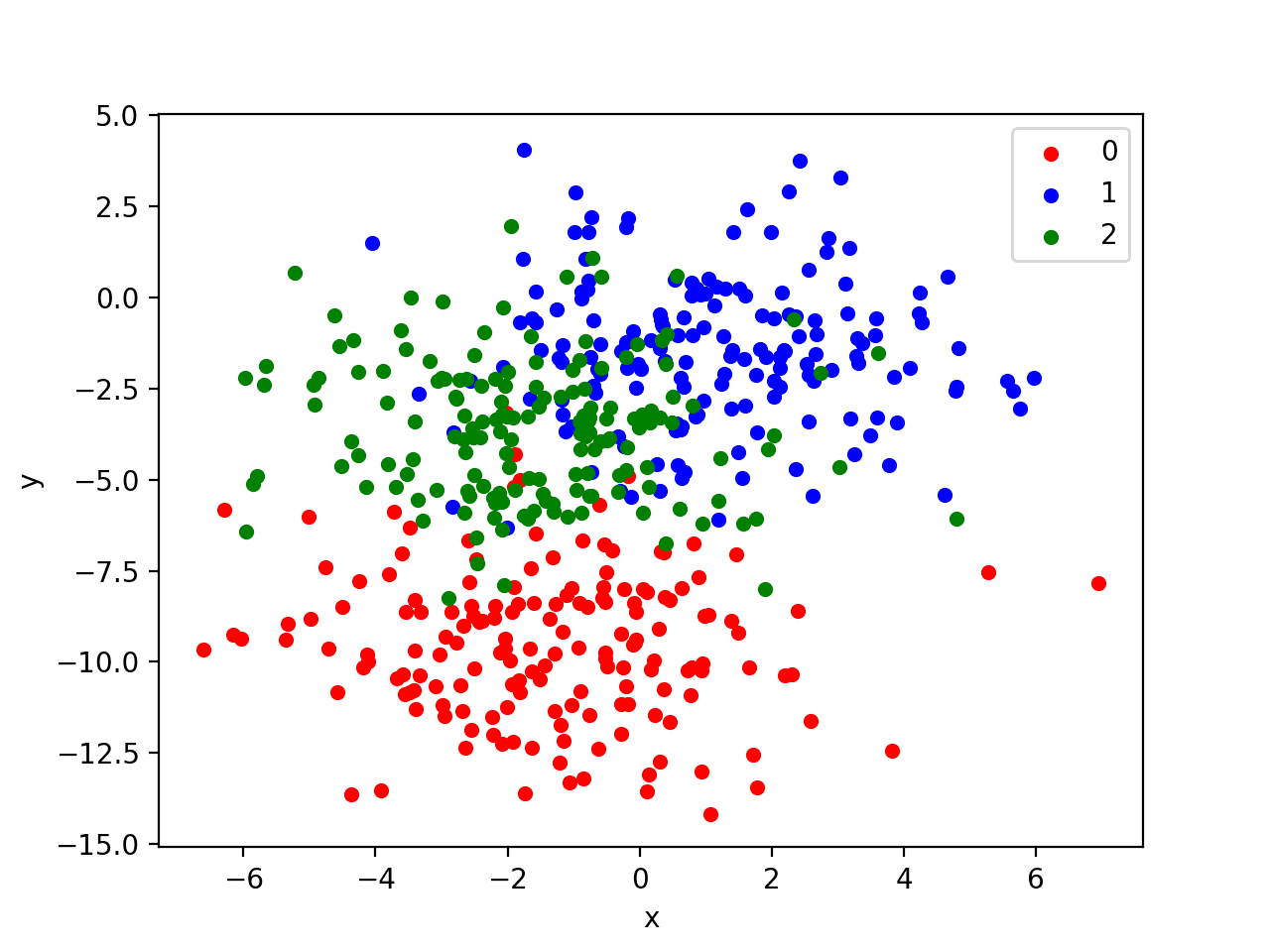
具有三个类别的 Blobs 数据集散点图,点按类别值着色
用于多类分类的 MLP 模型
既然我们已经定义了一个问题,我们就可以定义一个模型来解决它。
我们将定义一个可能约束不足且未针对问题进行调整的模型。这是有意的,以演示在真正大型和具有挑战性的监督学习问题上看到的神经网络模型的高方差。
该问题是一个多类分类问题,我们将使用输出层上的 softmax 激活函数对其进行建模。这意味着模型将预测一个包含 3 个元素的向量,其中包含样本属于 3 个类别中每个类别的概率。因此,第一步是对类别值进行独热编码。
|
1 |
y = to_categorical(y) |
接下来,我们必须将数据集分成训练集和测试集。我们将使用测试集来评估模型的性能,并使用学习曲线绘制其在训练过程中的性能。我们将使用 30% 的数据进行训练,70% 用于测试集。
这是一个具有挑战性的问题示例,其中我们有比标记示例更多的未标记示例。
|
1 2 3 4 |
# 分割成训练集和测试集 n_train = int(0.3 * X.shape[0]) trainX, testX = X[:n_train, :], X[n_train:, :] trainy, testy = y[:n_train], y[n_train:] |
接下来,我们可以定义并编译模型。
该模型将期望具有两个输入变量的样本。然后,模型有一个具有 15 个节点和整流线性激活函数的单个隐藏层,然后是一个具有 3 个节点以预测 3 个类别中每个类别的概率的输出层,以及一个 softmax 激活函数。
由于问题是多类问题,我们将使用分类交叉熵损失函数来优化模型,并使用高效的Adam 随机梯度下降变体。
|
1 2 3 4 5 |
# 定义模型 model = Sequential() model.add(Dense(15, input_dim=2, activation='relu')) model.add(Dense(3, activation='softmax')) model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy']) |
模型将训练 200 个训练周期,我们将在每个周期在测试集上评估模型,将测试集用作验证集。
|
1 2 |
# 拟合模型 history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0) |
在运行结束时,我们将评估模型在训练集和测试集上的性能。
|
1 2 3 4 |
# 评估模型 _, train_acc = model.evaluate(trainX, trainy, verbose=0) _, test_acc = model.evaluate(testX, testy, verbose=0) print('Train: %.3f, Test: %.3f' % (train_acc, test_acc)) |
最后,我们将绘制模型在每个训练周期在训练数据集和测试数据集上的准确率学习曲线。
|
1 2 3 4 5 |
# 绘制历史记录 pyplot.plot(history.history['accuracy'], label='train') pyplot.plot(history.history['val_accuracy'], label='test') pyplot.legend() pyplot.show() |
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
# 在 blobs 分类问题上拟合高方差 mlp from sklearn.datasets import make_blobs from keras.utils import to_categorical from keras.models import Sequential from keras.layers import Dense from matplotlib import pyplot # 生成二维分类数据集 X, y = make_blobs(n_samples=500, centers=3, n_features=2, cluster_std=2, random_state=2) y = to_categorical(y) # 分割成训练集和测试集 n_train = int(0.3 * X.shape[0]) trainX, testX = X[:n_train, :], X[n_train:, :] trainy, testy = y[:n_train], y[n_train:] # 定义模型 model = Sequential() model.add(Dense(15, input_dim=2, activation='relu')) model.add(Dense(3, activation='softmax')) model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy']) # 拟合模型 history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0) # 评估模型 _, train_acc = model.evaluate(trainX, trainy, verbose=0) _, test_acc = model.evaluate(testX, testy, verbose=0) print('Train: %.3f, Test: %.3f' % (train_acc, test_acc)) # 模型准确率的学习曲线 pyplot.plot(history.history['accuracy'], label='train') pyplot.plot(history.history['val_accuracy'], label='test') pyplot.legend() pyplot.show() |
运行示例首先会打印最终模型在训练集和测试集上的性能。
注意:由于算法或评估过程的随机性,或数值精度的差异,您的结果可能会有所不同。考虑多次运行示例并比较平均结果。
在这种情况下,我们可以看到模型在训练数据集上实现了约 84% 的准确率,在测试数据集上实现了约 76% 的准确率;不算太差。
|
1 |
训练:0.847,测试:0.766 |
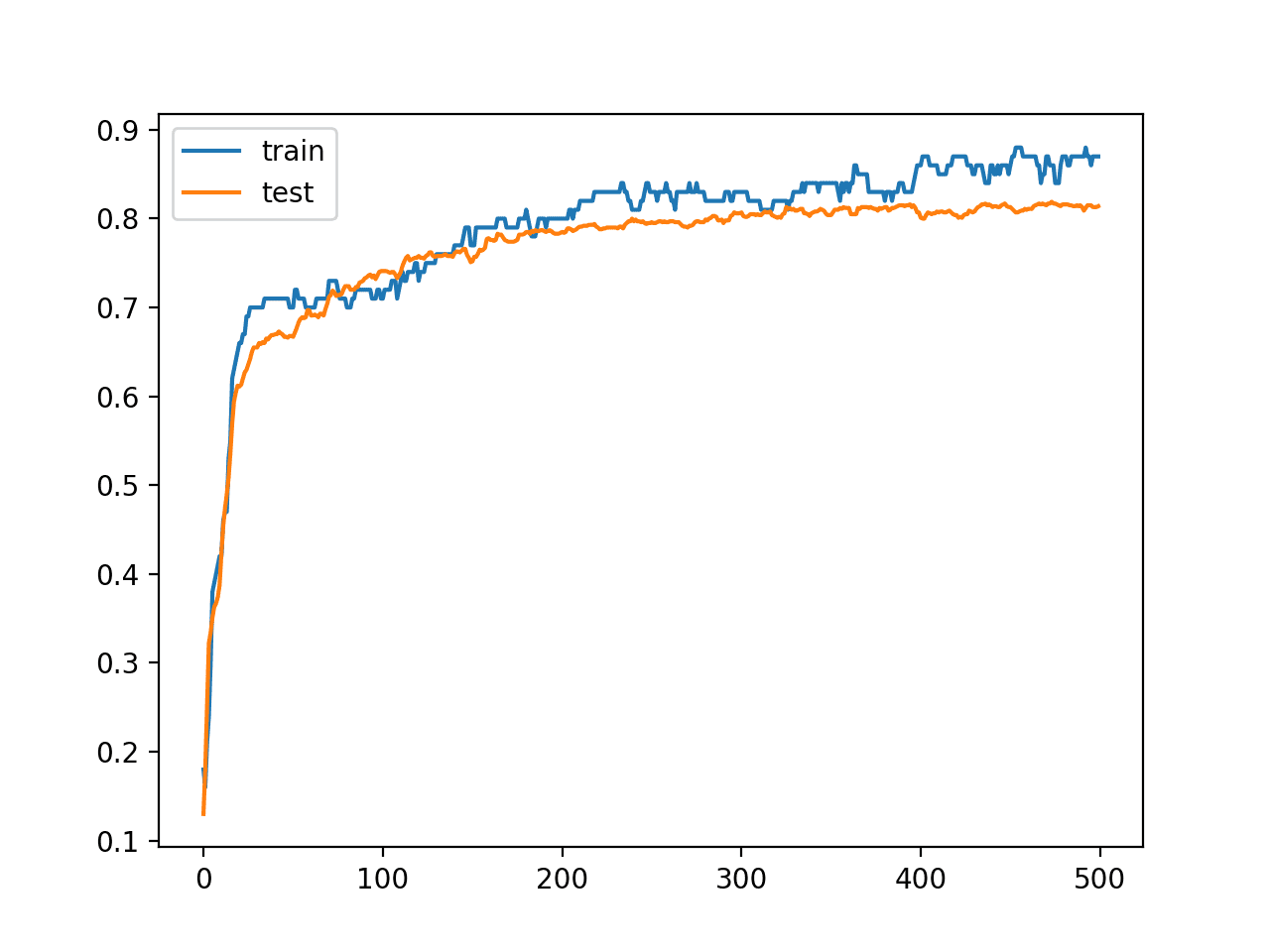
还创建了一条线图,显示了模型在训练集和测试集上每个训练周期的准确率学习曲线。
我们可以看到模型并没有真正过拟合,但可能有点欠拟合,并且可能受益于增加容量、更多训练以及一些正则化。我们故意保留所有这些改进,以强制我们的案例研究的高方差。
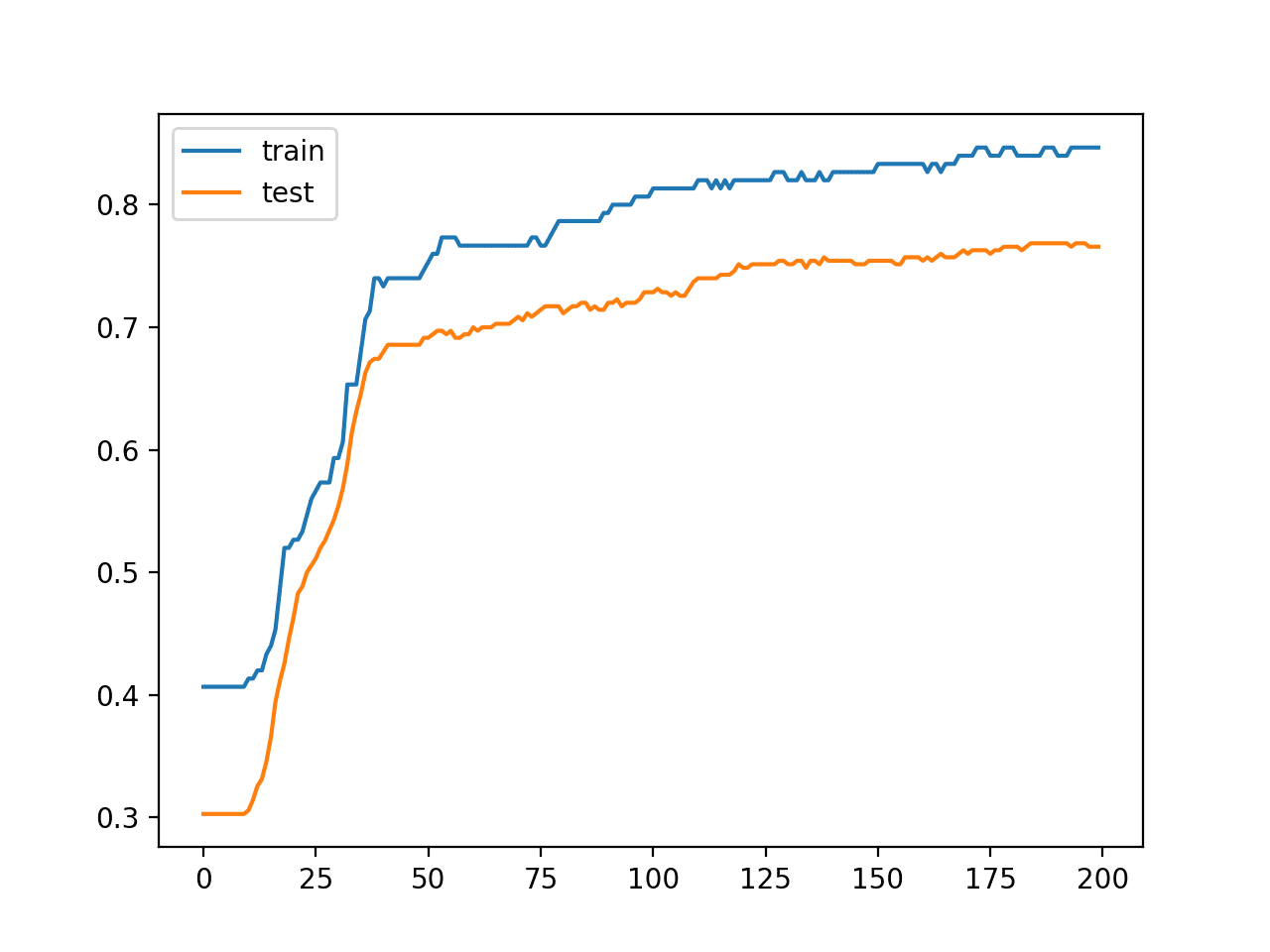
每个训练周期模型在训练和测试数据集上的准确率学习曲线图
MLP 模型的高方差
重要的是要证明模型确实在其预测中存在方差。
我们可以通过在相同数据集上重复拟合和评估相同的模型配置,并总结模型的最终性能来证明这一点。
为此,我们首先将模型的拟合和评估拆分为一个可以重复调用的函数。下面的 evaluate_model() 函数接受训练和测试数据集,拟合模型,然后评估它,返回模型在测试数据集上的准确率。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# 在数据集上拟合和评估神经网络模型 def evaluate_model(trainX, trainy, testX, testy): # 定义模型 model = Sequential() model.add(Dense(15, input_dim=2, activation='relu')) model.add(Dense(3, activation='softmax')) model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy']) # 拟合模型 model.fit(trainX, trainy, epochs=200, verbose=0) # 评估模型 _, test_acc = model.evaluate(testX, testy, verbose=0) return test_acc |
我们可以调用此函数 30 次,保存测试准确率分数。
|
1 2 3 4 5 6 7 |
# 重复评估 n_repeats = 30 scores = list() for _ in range(n_repeats): score = evaluate_model(trainX, trainy, testX, testy) print('> %.3f' % score) scores.append(score) |
收集到分数后,我们可以总结分数的分布,首先是平均值和标准差,假设分布是高斯分布,这是非常合理的。
|
1 2 |
# 总结分数分布 print('Scores Mean: %.3f, Standard Deviation: %.3f' % (mean(scores), std(scores))) |
然后,我们可以将分布概括为直方图,以显示分布的形状;概括为箱线图,以显示分布的扩展和主体。
|
1 2 3 4 5 6 |
# 分布直方图 pyplot.hist(scores, bins=10) pyplot.show() # 分布箱线图 pyplot.boxplot(scores) pyplot.show() |
下面列出了在所选 blobs 数据集上总结 MLP 模型方差的完整示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 |
# 演示 blobs 分类问题上 mlp 模型的高方差 from sklearn.datasets import make_blobs from keras.utils import to_categorical from keras.models import Sequential from keras.layers import Dense from numpy import mean from numpy import std from matplotlib import pyplot # 在数据集上拟合和评估神经网络模型 def evaluate_model(trainX, trainy, testX, testy): # 定义模型 model = Sequential() model.add(Dense(15, input_dim=2, activation='relu')) model.add(Dense(3, activation='softmax')) model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy']) # 拟合模型 model.fit(trainX, trainy, epochs=200, verbose=0) # 评估模型 _, test_acc = model.evaluate(testX, testy, verbose=0) return test_acc # 生成二维分类数据集 X, y = make_blobs(n_samples=500, centers=3, n_features=2, cluster_std=2, random_state=2) y = to_categorical(y) # 分割成训练集和测试集 n_train = int(0.3 * X.shape[0]) trainX, testX = X[:n_train, :], X[n_train:, :] trainy, testy = y[:n_train], y[n_train:] # 重复评估 n_repeats = 30 scores = list() for _ in range(n_repeats): score = evaluate_model(trainX, trainy, testX, testy) print('> %.3f' % score) scores.append(score) # 总结分数分布 print('Scores Mean: %.3f, Standard Deviation: %.3f' % (mean(scores), std(scores))) # 分布直方图 pyplot.hist(scores, bins=10) pyplot.show() # 分布箱线图 pyplot.boxplot(scores) pyplot.show() |
运行示例首先打印每个模型在测试集上的准确率,最后是准确率分数的样本均值和标准差。
注意:由于算法或评估过程的随机性,或数值精度的差异,您的结果可能会有所不同。考虑多次运行示例并比较平均结果。
在这种情况下,我们可以看到样本平均值是 77%,标准差约为 1.4%。假设是高斯分布,我们预计 99% 的准确率分数将落在约 73% 到 81% 之间(即高于和低于平均值 3 个标准差)。
我们可以将模型在测试集上的准确率的标准差作为模型预测方差的估计值。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
> 0.749 > 0.771 > 0.763 > 0.760 > 0.783 > 0.780 > 0.769 > 0.754 > 0.766 > 0.786 > 0.766 > 0.774 > 0.757 > 0.754 > 0.771 > 0.749 > 0.763 > 0.800 > 0.774 > 0.777 > 0.766 > 0.794 > 0.797 > 0.757 > 0.763 > 0.751 > 0.789 > 0.791 > 0.766 > 0.766 分数均值:0.770,标准差:0.014 |
还创建了一个准确率分数的直方图,显示了一个非常粗略的高斯形状,可能右侧有一个更长的尾部。
在图上使用更大的样本和不同数量的 bin 可能会更好地揭示分布的真实潜在形状。
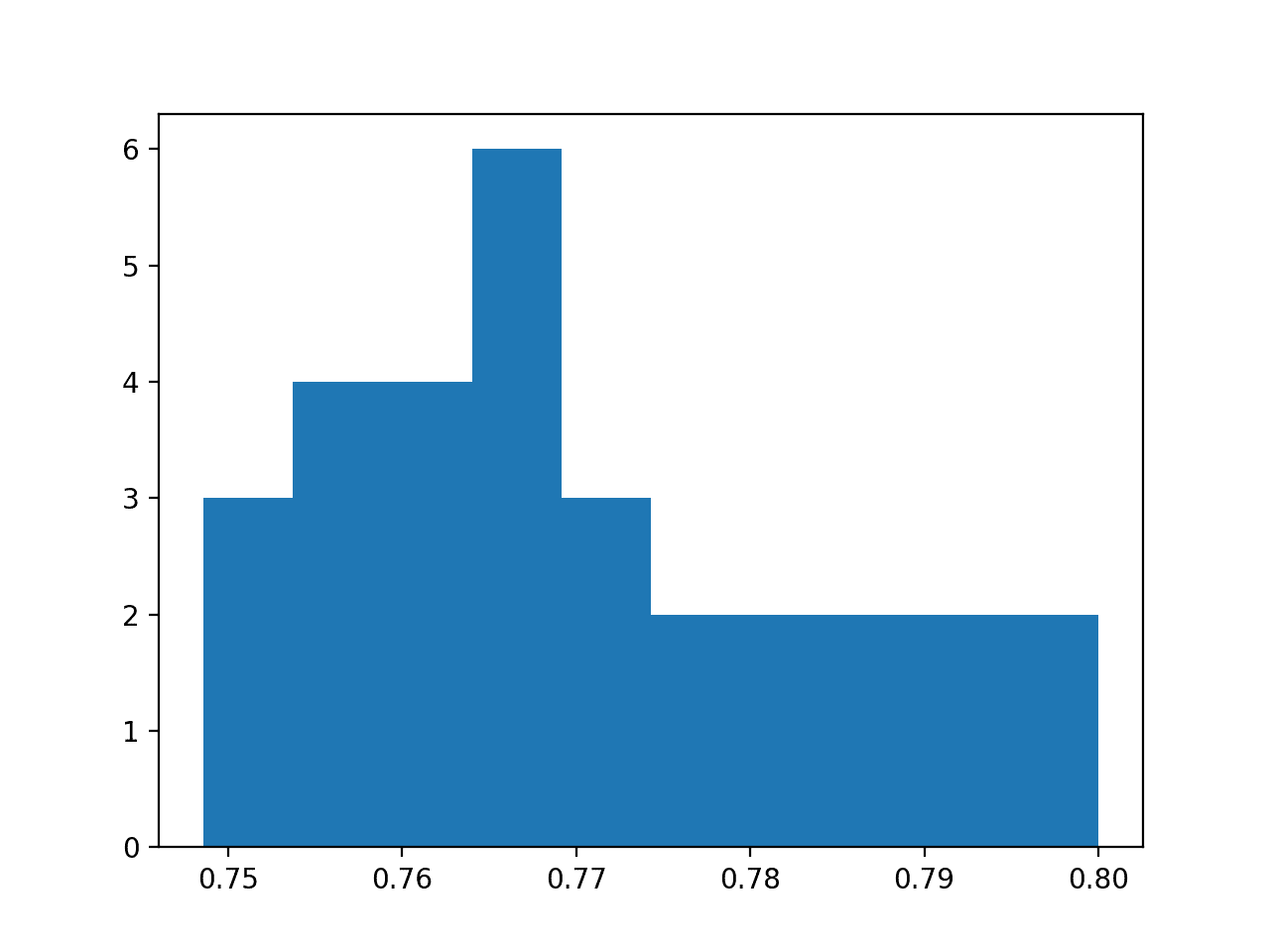
模型测试准确率在 30 次重复中的直方图
还创建了一个箱线图,显示中位数线在测试集上约为 76.5% 的准确率,以及四分位数范围或样本中间 50% 在约 78% 到 76% 之间。
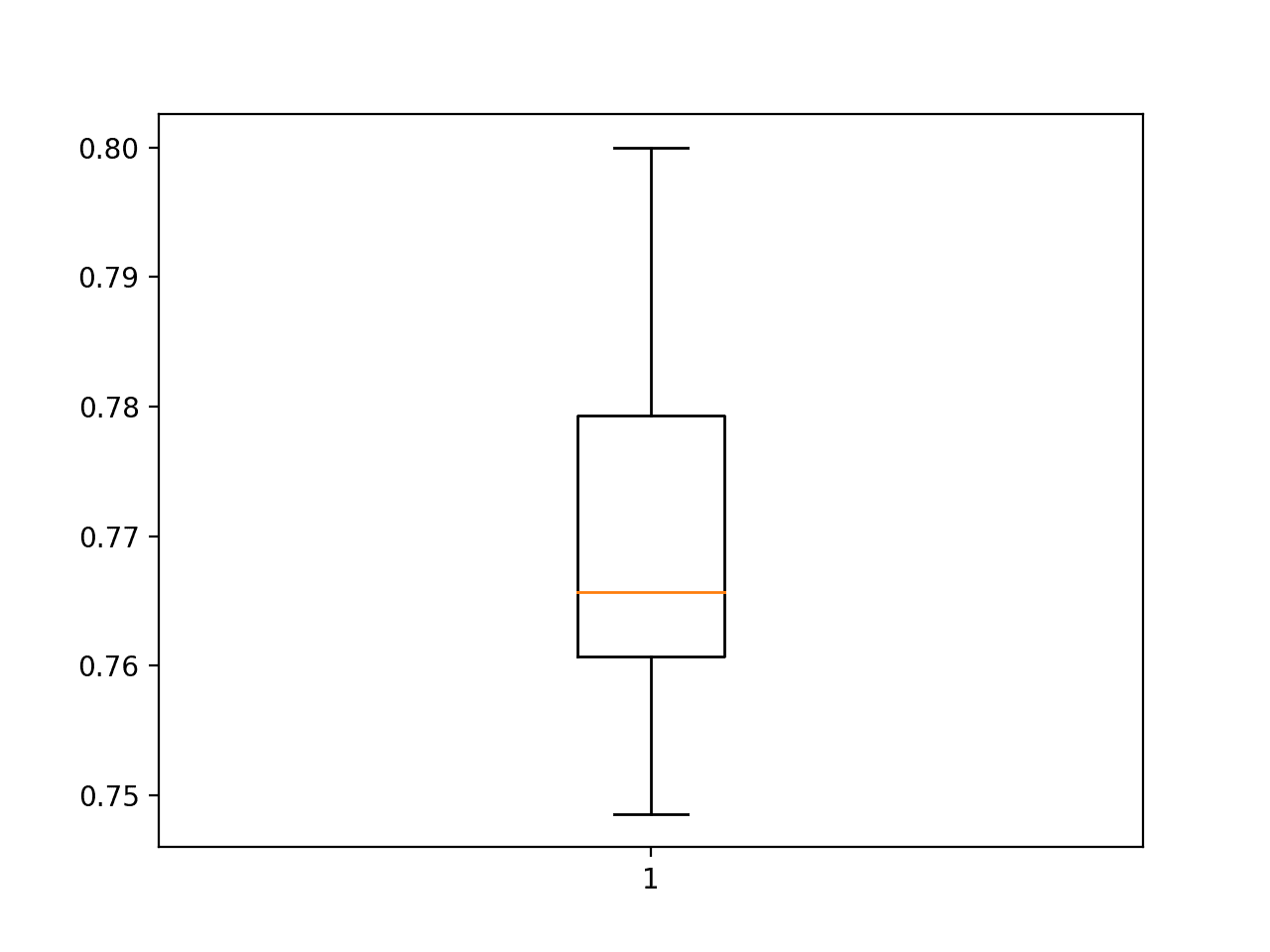
模型测试准确率在 30 次重复中的箱线图
对测试分数样本的分析清楚地表明,在相同数据集上训练的相同模型性能存在差异。
在测试集上可能得分的范围约为 8 个百分点(81% – 73%),可以合理地认为是大的,例如高方差结果。
模型平均集成
我们可以使用模型平均来减少模型的方差,并可能减少模型的泛化误差。
具体来说,这将导致保留测试集上的标准差更小,并且训练集上的性能更好。我们可以检查这两个假设。
首先,我们必须开发一个函数来准备并返回训练数据集上的拟合模型。
|
1 2 3 4 5 6 7 8 9 10 |
# 在数据集上拟合模型 def fit_model(trainX, trainy): # 定义模型 model = Sequential() model.add(Dense(15, input_dim=2, activation='relu')) model.add(Dense(3, activation='softmax')) model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy']) # 拟合模型 model.fit(trainX, trainy, epochs=200, verbose=0) return model |
接下来,我们需要一个函数,它可以接受集成成员列表并对样本外数据集进行预测。这可能是一个或多个样本,排列在样本和输入特征的二维数组中。
提示:您可以自己使用此函数来测试集成,并使用集成对新数据进行预测。
|
1 2 3 4 5 6 7 8 9 10 |
# 为多类分类进行集成预测 def ensemble_predictions(members, testX): # 进行预测 yhats = [model.predict(testX) for model in members] yhats = array(yhats) # 跨集成成员求和 summed = numpy.sum(yhats, axis=0) # 跨类求 argmax result = argmax(summed, axis=1) return result |
我们不知道这个集成需要多少个集成成员。
因此,我们可以对集成成员的数量进行敏感性分析,以及它如何影响测试准确率。这意味着我们需要一个函数,它可以评估指定数量的集成成员,并返回由这些成员组合而成的预测准确率。
|
1 2 3 4 5 6 7 8 9 |
# 评估集成中的特定数量成员 def evaluate_n_members(members, n_members, testX, testy): # 选择成员子集 subset = members[:n_members] print(len(subset)) # 进行预测 yhat = ensemble_predictions(subset, testX) # 计算准确率 return accuracy_score(testy, yhat) |
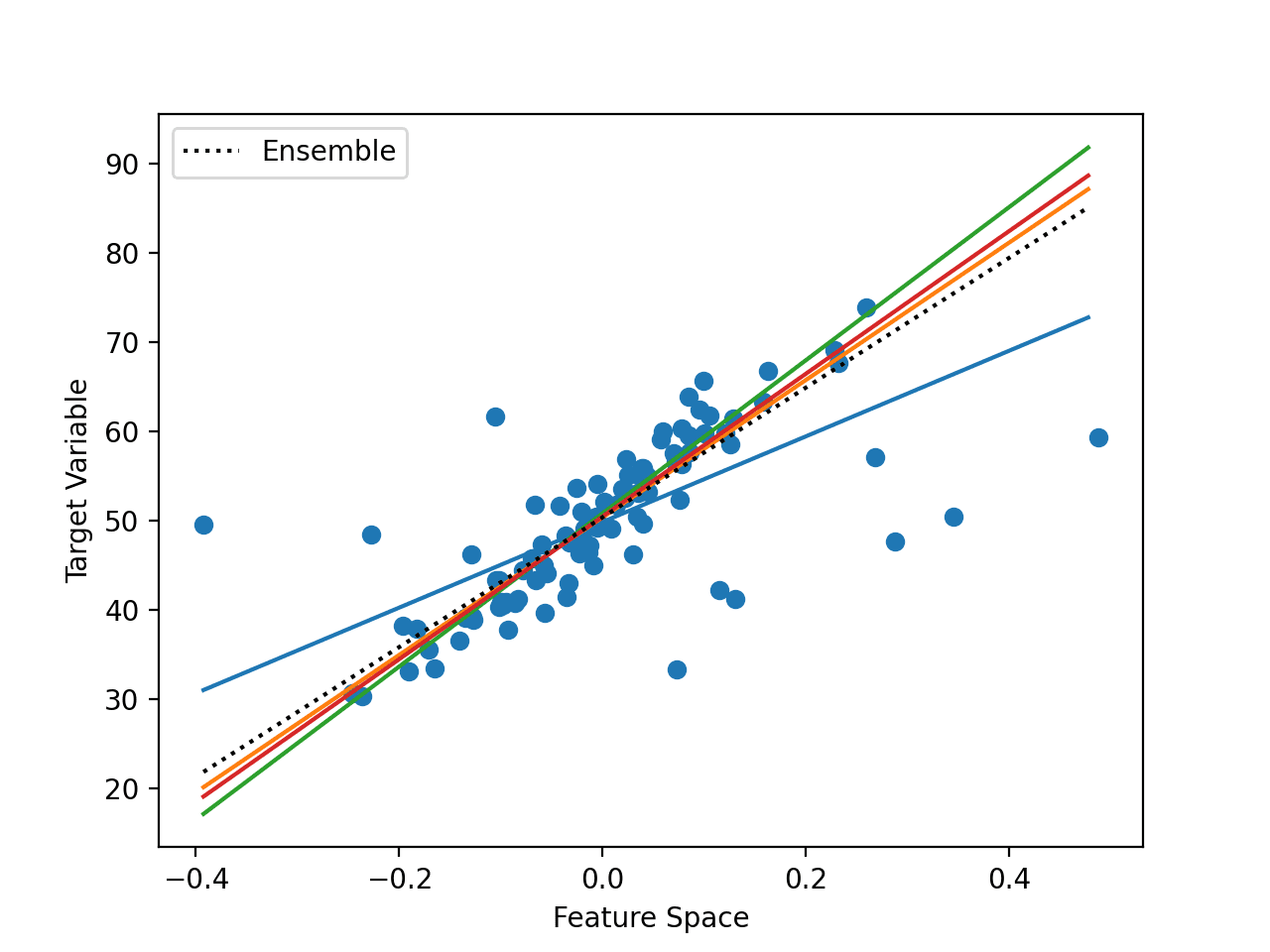
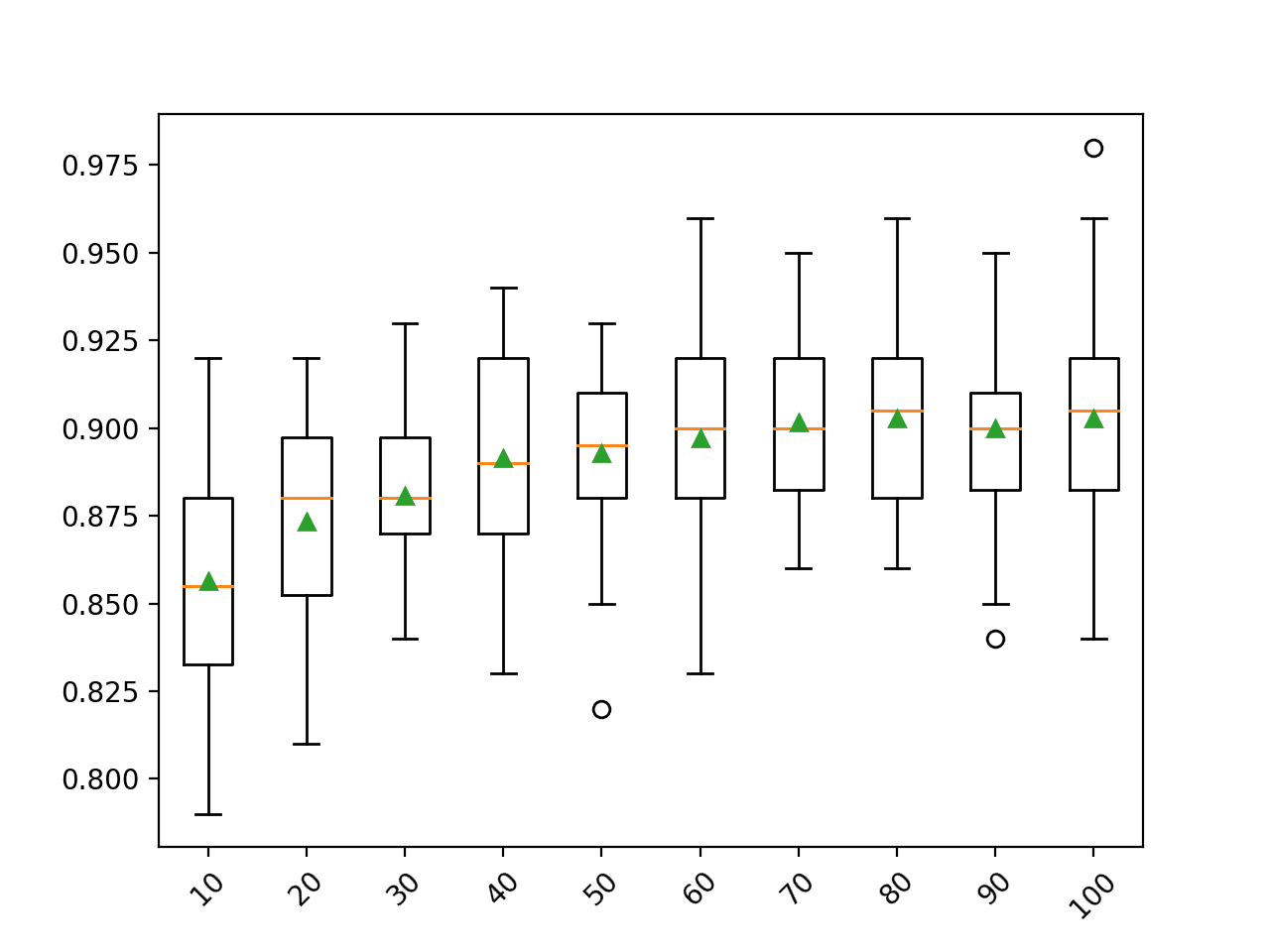
最后,我们可以绘制集成成员数量(x 轴)与在该数量成员上平均的预测在测试数据集上的准确率(y 轴)的线图。
|
1 2 3 4 |
# 绘制分数与集成成员数量的关系 x_axis = [i for i in range(1, n_members+1)] pyplot.plot(x_axis, scores) pyplot.show() |
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 |
# 模型平均集成和集成大小对测试准确率的研究 from sklearn.datasets import make_blobs from keras.utils import to_categorical from keras.models import Sequential from keras.layers import Dense import numpy from numpy import array from numpy import argmax from sklearn.metrics import accuracy_score from matplotlib import pyplot # 在数据集上拟合模型 def fit_model(trainX, trainy): # 定义模型 model = Sequential() model.add(Dense(15, input_dim=2, activation='relu')) model.add(Dense(3, activation='softmax')) model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy']) # 拟合模型 model.fit(trainX, trainy, epochs=200, verbose=0) return model # 为多类分类进行集成预测 def ensemble_predictions(members, testX): # 进行预测 yhats = [model.predict(testX) for model in members] yhats = array(yhats) # 跨集成成员求和 summed = numpy.sum(yhats, axis=0) # 跨类求 argmax result = argmax(summed, axis=1) return result # 评估集成中的特定数量成员 def evaluate_n_members(members, n_members, testX, testy): # 选择成员子集 subset = members[:n_members] print(len(subset)) # 进行预测 yhat = ensemble_predictions(subset, testX) # 计算准确率 return accuracy_score(testy, yhat) # 生成二维分类数据集 X, y = make_blobs(n_samples=500, centers=3, n_features=2, cluster_std=2, random_state=2) # 分割成训练集和测试集 n_train = int(0.3 * X.shape[0]) trainX, testX = X[:n_train, :], X[n_train:, :] trainy, testy = y[:n_train], y[n_train:] trainy = to_categorical(trainy) # 拟合所有模型 n_members = 20 members = [fit_model(trainX, trainy) for _ in range(n_members)] # 评估不同数量的集成 scores = list() for i in range(1, n_members+1): score = evaluate_n_members(members, i, testX, testy) print('> %.3f' % score) scores.append(score) # 绘制分数与集成成员数量的关系 x_axis = [i for i in range(1, n_members+1)] pyplot.plot(x_axis, scores) pyplot.show() |
运行示例首先在相同的训练数据集上拟合 20 个模型,这在现代硬件上可能需要不到一分钟的时间。
注意:由于算法或评估过程的随机性,或数值精度的差异,您的结果可能会有所不同。考虑多次运行示例并比较平均结果。
然后,测试不同大小的集成,从 1 个成员到所有 20 个成员,并为每个集成大小打印测试准确率结果。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
1 > 0.740 2 > 0.754 3 > 0.754 4 > 0.760 5 > 0.763 6 > 0.763 7 > 0.763 8 > 0.763 9 > 0.760 10 > 0.760 11 > 0.763 12 > 0.763 13 > 0.766 14 > 0.763 15 > 0.760 16 > 0.760 17 > 0.763 18 > 0.766 19 > 0.763 20 > 0.763 |
最后,创建一条线图,显示集成大小与测试集性能之间的关系。
我们可以看到性能在约五个成员时有所提高,之后性能稳定在约 76% 的准确率。这接近在模型重复评估分析中观察到的平均测试集性能。
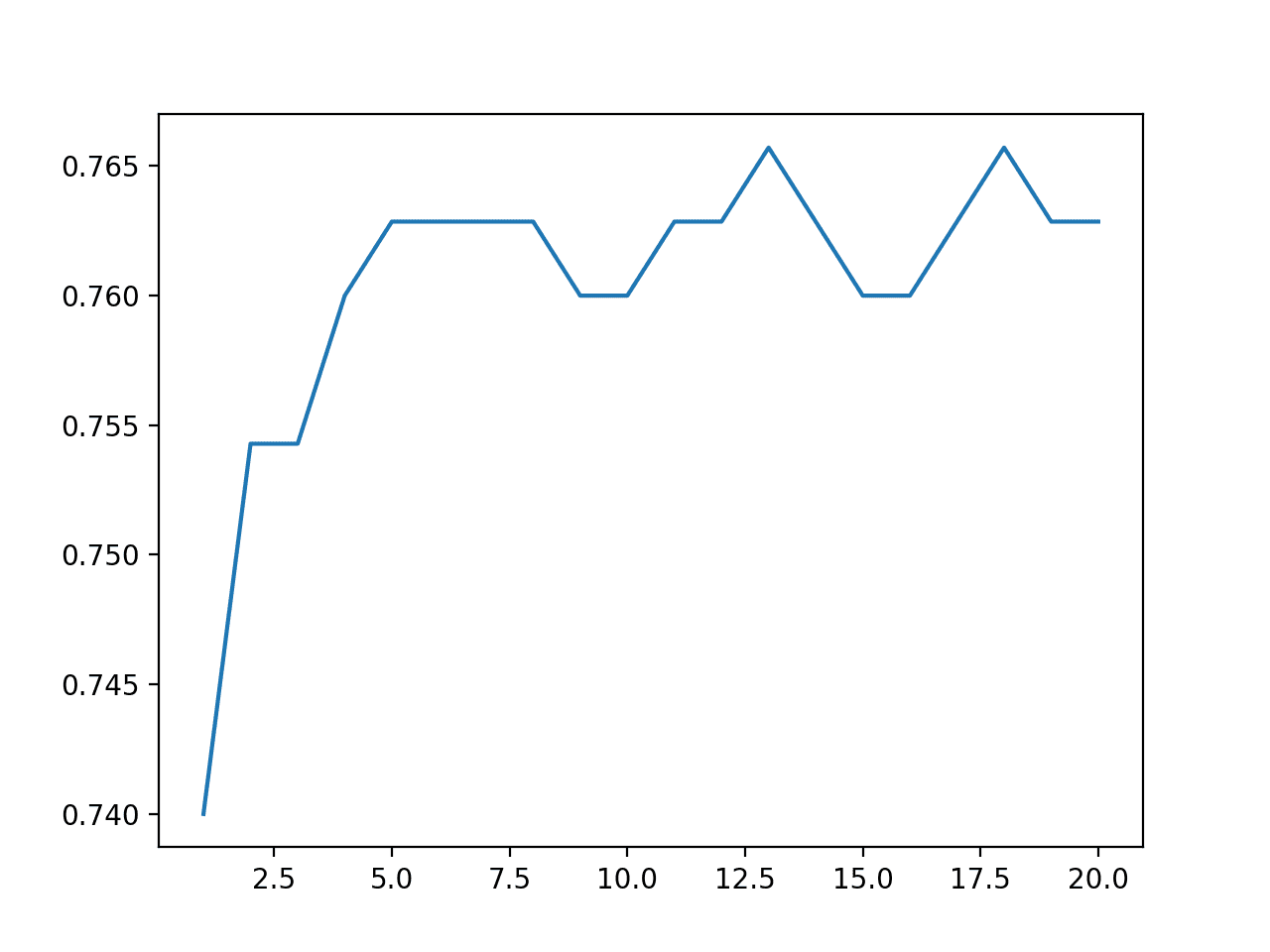
集成大小与模型测试准确率的线图
最后,我们可以更新重复评估实验,使用五个模型的集成而不是单个模型,并比较分数的分布。
下面列出了 blobs 数据集上五成员集成模型平均的重复评估的完整示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 |
# 对 blobs 数据集进行模型平均集成的重复评估 from sklearn.datasets import make_blobs from keras.utils import to_categorical from keras.models import Sequential from keras.layers import Dense import numpy from numpy import array from numpy import argmax from numpy import mean from numpy import std from sklearn.metrics import accuracy_score # 在数据集上拟合模型 def fit_model(trainX, trainy): # 定义模型 model = Sequential() model.add(Dense(15, input_dim=2, activation='relu')) model.add(Dense(3, activation='softmax')) model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy']) # 拟合模型 model.fit(trainX, trainy, epochs=200, verbose=0) return model # 为多类分类进行集成预测 def ensemble_predictions(members, testX): # 进行预测 yhats = [model.predict(testX) for model in members] yhats = array(yhats) # 跨集成成员求和 summed = numpy.sum(yhats, axis=0) # 跨类求 argmax result = argmax(summed, axis=1) return result # 评估集成模型 def evaluate_members(members, testX, testy): # 进行预测 yhat = ensemble_predictions(members, testX) # 计算准确率 return accuracy_score(testy, yhat) # 生成二维分类数据集 X, y = make_blobs(n_samples=500, centers=3, n_features=2, cluster_std=2, random_state=2) # 分割成训练集和测试集 n_train = int(0.3 * X.shape[0]) trainX, testX = X[:n_train, :], X[n_train:, :] trainy, testy = y[:n_train], y[n_train:] trainy = to_categorical(trainy) # 重复评估 n_repeats = 30 n_members = 5 scores = list() for _ in range(n_repeats): # 拟合所有模型 members = [fit_model(trainX, trainy) for _ in range(n_members)] # 评估集成 score = evaluate_members(members, testX, testy) print('> %.3f' % score) scores.append(score) # 总结分数分布 print('Scores Mean: %.3f, Standard Deviation: %.3f' % (mean(scores), std(scores))) |
运行此示例可能需要几分钟,因为要拟合和评估五个模型,并且此过程重复 30 次。
每个模型在测试集上的性能都会打印出来,以指示进度。
注意:由于算法或评估过程的随机性,或数值精度的差异,您的结果可能会有所不同。考虑多次运行示例并比较平均结果。
模型性能的均值和标准差在运行结束时打印。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
> 0.769 > 0.757 > 0.754 > 0.780 > 0.771 > 0.774 > 0.766 > 0.769 > 0.774 > 0.771 > 0.760 > 0.766 > 0.766 > 0.769 > 0.766 > 0.771 > 0.763 > 0.760 > 0.771 > 0.780 > 0.769 > 0.757 > 0.769 > 0.771 > 0.771 > 0.766 > 0.763 > 0.766 > 0.771 > 0.769 分数均值:0.768,标准差:0.006 |
在这种情况下,我们可以看到该数据集上五成员集成的平均性能为 76%。这与单个模型的平均 77% 非常接近。
重要的区别是标准差从单个模型的 1.4% 缩小到五模型集成的 0.6%。我们可能会预计,在这个问题上,一个给定的五模型集成在 99% 的可能性下,其性能将介于 74% 到 78% 之间。
对在相同数据集上训练的相同模型进行平均,可以提高可靠性,这是最终模型在实际操作中通常非常需要的属性。
集成中的更多模型将进一步减小测试数据集上集成准确率的标准差,根据大数定律,至少到收益递减点为止。
这表明,对于这个特定的模型和预测问题,一个包含五个成员的模型平均集成足以减少模型的方差。方差的这种减少反过来也意味着在准备最终模型时平均性能更好。
扩展
本节列出了一些您可能希望探索的扩展本教程的想法。
- 平均类别预测。更新示例,平均类别整数预测而不是类别概率预测并比较结果。
- 保存和加载模型。更新示例,将集成成员保存到文件,然后从单独的脚本加载它们进行评估。
- 方差敏感性。创建一个新示例,对集成成员的数量对模型在给定重复次数下的测试集性能标准差进行敏感性分析,并报告收益递减点。
如果您探索了这些扩展中的任何一个,我很想知道。
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
总结
在本教程中,您学习了如何在 Keras 中开发模型平均集成,以减少最终模型的方差。
具体来说,你学到了:
- 模型平均是一种集成学习技术,可用于减少深度学习神经网络模型的预期方差。
- 如何在 Keras 中实现分类和回归预测建模问题的模型平均。
- 如何解决多类分类问题,并使用模型平均来减少最终模型的方差。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。


你好 Jason,一如既往的精彩帖子!我对音频/声音处理以及机器学习/深度学习在其中的应用非常感兴趣。图像处理在机器学习领域得到了很好的覆盖。不幸的是,音频/声音却没有。我想知道您是否能给我推荐一些关于这个主题的知识来源?或者更好的是,任何介绍性博客文章都会非常感谢 😉
我希望将来能涉及这个话题,谢谢您的建议。
很棒的帖子。它有助于学习很多关于集成模型预测的知识。但是,我不确定如何在此示例中使用 model.save() 来保存具有最佳成员数量的集成模型。您能否告诉我如何将集成成员保存到文件以供进一步部署?谢谢。
是的,请参阅本教程
https://machinelearning.org.cn/save-load-keras-deep-learning-models/
感谢 Jason 的精彩帖子。我认为我们不能使用 model.save() 来保存集成模型,因为模型没有定义。我们只得到了集成模型预测,而不是模型本身。非常感谢您的建议。
您可以保存集成的元素。
谢谢 Jason。很抱歉,我不明白。
我读了您列出的教程。它都是关于使用定义的模型来保存模型本身或模型的权重或模型的架构。我不知道如何保存集成的元素。它们是权重吗?我不这么认为。
当我们想要输出最终模型以预测新数据时,我们必须有一个保存的模型,而不是重新执行“加载几个保存的模型,集成在一起,然后得到预测”。我希望如果我有一个保存的集成模型,我可以使用 model.prediction()。
您能否给我们一个示例或几行代码来展示如何保存集成的元素?非常感谢。
不客气。
您可以对每个模型调用 save() 并保存到单独的文件中,然后稍后加载并用于进行预测。
我相信有很多例子,这里有一个
https://machinelearning.org.cn/horizontal-voting-ensemble/
Jason,很棒的帖子,
我假设代码开头设置种子以获得可复现结果不再有意义,对吗?
另外,我想知道,使用集成方法运行 RandomizedSearchCV 是否是常见做法?我的意思是,在函数 fit_model(params) 中,我们可以这样写:rs = RandomizedSearchCV(…); model=rs.fit(X,y)。代码的其余部分是相同的
我不推荐这种方法,因为您仍然会从输入数据中获得差异。更多信息在这里
https://machinelearning.org.cn/faq/single-faq/why-do-i-get-different-results-each-time-i-run-the-code
如果您有资源,以任何方式进行网格搜索都是一个好主意。
只是为了确保我理解:像链接中那样设置种子对于集成来说不是一个好主意。对吗?
是的,事实上,我一般不推荐它用于神经网络。
相反,最好管理模型和数据中的方差。
太棒了,因为你用真实代码解释了集成,所以我清楚地理解了它。
谢谢 Jason
谢谢。
非常感谢!
不客气。
你好,
当我尝试使用与此博客中相同的方法来集成二元模型 (14) 来解决多类问题时,我收到以下错误;
ValueError: 分类指标无法处理多标签指示器和二元目标的混合
我正在加载已经拟合到我的数据中的二元模型来预测一些测试数据。当我使用来自预测的输出数组到 sklearn 准确率分数函数时。我收到该错误。我该如何解决这个问题?我如何像 OVA 系统一样将二元模型连接起来进行多类预测
我不确定,您需要调试故障。
先生,我是一名计算机科学学士学位的研究学生,我的任务是集成三个深度学习 CNN 预训练模型。我正在使用预训练模型,但我不明白如何在 Matlab 中使用平均、多数投票和加权平均方法集成它们的结果。您能否帮助我如何进行。
提前感谢。
等待您的指导。
抱歉,我没有 Matlab 的教程。
嗨 Jason,非常感谢您有用的教程。我想组合一些模型,而不是它们预测的输出。类似串联,向输出添加一个新层,......
我的问题是我想找到一种方法来解释模型是如何组合的,例如,能够给每个模型赋予权重,然后通过平均来组合它们?
总而言之,您能告诉我一些组合模型的方法,而不是结果吗?
用于组合模型预测(例如加权平均)的权重可能会提供对模型如何用于创建最终输出的洞察。
真棒!
一个问题。我有一个不平衡的数据集,所以我进行了过采样,之后神经网络的表现不是很好。我尝试像您一样进行神经网络集成,但什么都没有!准确率总是很低,与其他模型(SVC、逻辑回归)相比,它们的准确率非常高。
我的数据集可能无法用神经网络训练吗?
也许尝试其他模型类型?
也许尝试其他模型架构?
也许尝试其他学习配置?
也许尝试其他数据准备?
1) 我做了
2) 我做了
3) 我做了
4) 我做了
🙂
这里还有更多想法
https://machinelearning.org.cn/start-here/#better
一旦您用尽了所有想法,也许是时候开始一个新项目了。
祝贺您的教程!
我不明白为什么我们必须制作斑点。
谢谢
看起来像聚类学习
谢谢。
我们不必。我们正在使用斑点数据集作为探索模型的基础。
嗨,Jason,
这是一个很棒的教程,我已经把它加到书签了。我困惑了很久的集成训练问题。阅读后,我明白了它基本上是通过不同的模型进行训练并对它们的预测进行平均,以平衡高方差和高偏差。我说的对吗?我以前只训练一个最好的模型,但正如您所说。即使它对验证数据集看起来不错,但对测试数据集来说可能不是最好的。非常感谢。
正确。
嗨,Jason,
刚开始研究集成学习,并阅读了您的几篇博客。在另一篇博客中提到了
个体验证误差
googlenet: 7.23%
squeezneet: 12.89%
resnet18: 7.75%
xception: 3.92%
mobilenetv2: 6.96%
模型集成误差
平均:3.56%
加权平均:3.28%(Xception 计数两次)。
多数投票:4.04%
我想知道这些集成值是如何计算的,因为它似乎不是普通的平均值。是否存在一个用于得出答案的隐藏函数。如果单个结果相同,答案是否会始终相同?
与此相关,我想知道对于多类分类,如果我使用 100 个类训练模型,然后使用 70 个类,然后使用 50 个类。我如何集成(如果可能的话),以及如何解释,因为使用较少的类很可能会有更高的准确率。
谢谢。
您需要查看报告结果的论文。它们看起来很直接,平均值就是均值,加权平均值是使用模型技能作为权重或软投票,多数投票是使用硬投票。
如果模型预测的是不同的类组,那么集成可能就没有意义了。
谢谢。我会写信给作者,但想听听您的专家意见,它来自 MathWorks 网站的一篇博客文章
https://blogs.mathworks.com/deep-learning/2019/06/03/ensemble-learning/
在评论区解释道(我在这里写的是平均值)
predictionsMean = mean(predictionsAllModels,3);
%predictionsAllModels 只是所有模型(从“分类”获得概率)的输出:%predictionsAllModels(:,:,i) = probs;
到这里为止都没问题。
getEnsembleError(predictionsMean, YValidation, labels);
我想知道的是,这些 YValidation 和标签是来自第一个、第二个……模型,还是我们需要再次运行代码?
该函数写成:
function getEnsembleError(predictions, YValidation, labels)
[~,mi] = max(predictions,[],2);
predLabels = labels(mi);
validationErrorMean = mean(predLabels ~= YValidation);
disp(“Ensemble validation error: ” + validationErrorMean*100 + “%”)
结束
抱歉,我没有能力审查第三方代码。
https://machinelearning.org.cn/faq/single-faq/can-you-explain-this-research-paper-to-me
很抱歉问了这个问题。
一个关于集成(ensembling)的澄清问题:
在进行集成后,我们是否会得到一个最终模型,可以应用于测试/未见数据?还是我们必须再次在测试数据上运行各个网络/模型,然后对其进行相同的聚合操作?
谢谢。
集成本身就是最终模型,用于对新数据进行预测。
嗨,Jason,为什么将测试数据传递给 model.predict 而不是 model.evaluate?
另外,20个模型在 model.predict 上运行,然后对其分数进行平均。在测试集上 model.evaluate 的分数平均值会表示什么?我不明白其中的区别。
在这些模型(无论是 model.predict 还是 model.evaluate)平均完成后,我怎么知道哪个是我的最终模型?所有20个模型都将是我的最终模型吗?例如,在实际场景中,我需要向客户提交一个模型,我怎么知道提交哪一个?
在这里使用 model.evaluate() 是无效的。
为了做出可以手动评估的预测。
你好 Jason,
感谢这篇精彩的教程。我一直觉得深度学习集成会以这种方式工作,您的文章正好证实了我的想法😉。
我在这篇帖子中看到一个图像分类器集成设计(Faisal,2020年7月23日上午1:07),其中加权平均技术将误差降低到一个类似于“平均值”的值(3.56%),即使没有单个模型达到该性能。那么,比方说,我有5个深度学习模型,每个模型的准确率约为80%。如果我实施任何集成技术,我能期望准确率有所提高吗?为了示例的目的,假设准确率是最好的度量标准。
感谢您的关注,并请继续保持出色的工作。
不客气!
也许可以尝试一下。
嗨,Jason,感谢您出色的教程。
只是为了澄清。您使用了“模型平均集成”这个术语,但您使用了“numpy.sum”来在模型之间进行集成。所以您指的是求和集成。对吗?
在我看来,我期望使用 Keras 中已经提供的平均层。其他层可能也适用。这里的挑战在于哪种操作最适合集成(求和、相乘、平均等)。
对于分类预测,“平均”有两种方式,如帖子中所述:第一种是类别标签的统计众数,称为“硬投票”(hard voting);第二种是预测概率之和的 argmax,称为“软投票”(soft voting)。
Keras 中的平均层无法实现这一点。
感谢这篇精彩的教程,
我是机器学习新手,我正在尝试在我的模型中使用模型平均集成进行回归任务。我使用这部分代码来组合预测:
yhats = [model.predict(testX) for model in models]
yhats = array(yhats)
# 计算平均值
outcomes = mean(yhats)
此外,我通过均方误差来衡量集成的准确性,但是,在最终结果中,均方误差没有任何变化,无论模型数量如何。我的意思是,均方误差在模型数量上保持不变。
因此,我想知道这种行为是否可能以及为什么?您能帮我解决这个问题吗?
此外,如果您能提供一个回归示例,那将很有帮助。
也许您需要调整集成中使用的模型?
也许这些模型不适合您的问题?
也许集成无法改善您问题的性能?
你好,
如果只是输出的平均值,模型是如何改进如此之多的?这不清楚。
实际上,这不应该感到惊讶。对于一个模型,其预测具有一定的方差(由标准差衡量)。对于N个模型,平均预测的方差会减少根号N倍。
我如何提取和保存平均预测?我还想绘制 epoch 对 MSE 的历史图,这些集成代码可以实现吗?
嗨,Farha……您可能会对以下资源感兴趣:
https://machinelearning.org.cn/stacking-ensemble-machine-learning-with-python/