蒙特卡洛方法是一类通过随机采样概率分布的技术。
在许多问题领域中,描述或估计概率分布相对简单,但计算所需量却非常困难。这可能由许多原因引起,例如域的随机性质或指数级的随机变量数量。
相反,可以通过使用随机采样来近似所需量,这被称为蒙特卡洛方法。这些方法最初在第一台计算机出现时就被使用,并且至今在包括人工智能和机器学习在内的所有科学和工程领域中都普遍存在。
在本文中,您将了解用于采样概率分布的蒙特卡洛方法。
阅读本文后,你将了解:
- 通常,我们无法计算概率中的所需量,但我们可以直接或间接定义随机变量的概率分布。
- 蒙特卡洛采样是用于从概率分布中随机采样的一类方法。
- 蒙特卡洛采样为许多机器学习方法提供了基础,例如重采样、超参数调整和集成学习。
启动您的项目,阅读我的新书 机器学习中的概率,其中包含分步教程和所有示例的Python源文件。
让我们开始吧。

概率的蒙特卡洛采样入门
照片来源:Med Cruise Guide,部分权利保留。
概述
本教程分为三个部分;它们是:
- 采样的必要性
- 什么是蒙特卡洛方法?
- 蒙特卡洛方法的示例
采样的必要性
在概率以及更广泛的机器学习领域中,有许多问题是我们无法直接计算出解析解的。
事实上,对于大多数实际的概率模型来说,精确推理可能是难以处理的。
对于大多数具有实际意义的概率模型,精确推理是难以处理的,因此我们必须采取某种形式的近似。
— 第 523 页,《模式识别与机器学习》,2006 年。
所需的计算通常是对离散分布的求和或对连续分布的积分,并且难以计算。由于随机变量数量众多、域的随机性质、观测中的噪声、观测的缺乏等等原因,计算可能变得难以处理。
在这一类问题中,通常可以定义或估计所涉及的随机变量的概率分布,无论是直接还是间接通过计算模拟。
与其直接计算该量,不如使用采样。
采样提供了一种灵活的方式,以较低的成本近似许多求和和积分。
— 第 590 页,《深度学习》,2016 年。
可以从概率分布中随机抽取样本,并用于近似所需的量。
这种从概率分布中随机采样的一般类技术被称为蒙特卡洛方法。
想学习机器学习概率吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
什么是蒙特卡洛方法?
蒙特卡洛方法,简称 MC,是一类用于随机采样概率分布的技术。
使用蒙特卡洛方法随机采样概率分布主要有三个原因:
- 估计密度,收集样本以近似目标函数的分布。
- 近似一个量,例如分布的均值或方差。
- 优化一个函数,定位最大化或最小化目标函数的样本。
蒙特卡洛方法以摩纳哥的赌场命名,并首次在第一台计算机和曼哈顿计划(开发第一颗原子弹)的开发时期被用于解决粒子物理学中的问题。
这被称为蒙特卡洛近似,以欧洲一座以其豪华赌场闻名的城市命名。蒙特卡洛技术最初是在统计物理学领域开发的——尤其是在原子弹的开发过程中——但现在在统计学和机器学习中也得到了广泛应用。
— 第 52 页,《机器学习:概率视角》,2012 年。
抽取样本可能只是计算随机选择事件的概率,也可能复杂到运行计算模拟,后者通常被称为蒙特卡洛模拟。
收集多个样本并用于近似所需的量。
根据统计学中的大数定律,执行的随机试验越多,近似量就越准确。
…大数定律指出,如果样本 x(i) 是独立同分布的,则平均值几乎肯定收敛到期望值
— 第 591 页,《深度学习》,2016 年。
因此,样本数量可以控制被近似量的精度,通常受抽取样本的计算复杂度的限制。
通过生成足够的样本,我们可以达到任何想要的精度级别。主要问题是:我们如何有效地从概率分布中生成样本,尤其是在高维度的情况下?
— 第 815 页,《机器学习:概率视角》,2012 年。
此外,根据中心极限定理,样本的分布将形成正态分布,其均值可作为近似量,方差可用于提供该量的置信区间。
中心极限定理告诉我们,平均值的分布 [...] 收敛于正态分布 [...] 这使得我们能够使用正态密度函数的累积分布来估计估计值周围的置信区间 [...]。
— 第 592 页,《深度学习》,2016 年。
蒙特卡洛方法根据样本的抽取方式或对采样过程施加的约束来定义。
蒙特卡洛采样方法的一些例子包括:直接采样、重要性采样和拒绝采样。
- 直接采样。在没有先验信息的情况下直接对分布进行采样。
- 重要性采样。从目标分布的更简单的近似中进行采样。
- 拒绝采样。从更广泛的分布中进行采样,并仅考虑在采样分布的某个区域内的样本。
这是一个庞大的主题,有许多书籍专门介绍。接下来,让我们通过一些熟悉的例子来具体化蒙特卡洛采样的概念。
蒙特卡洛采样示例
我们一直在不自觉地使用蒙特卡洛方法。
例如,当我们为抛硬币定义一个伯努利分布,并通过从该分布采样来模拟抛硬币时,我们就在执行蒙特卡洛模拟。此外,当我们从 {1,2,3,4,5,6} 的整数均匀分布中采样来模拟掷骰子时,我们也在执行蒙特卡洛模拟。
当我们从域中收集随机数据样本并使用直方图或密度估计方法估计数据概率分布时,我们也正在使用蒙特卡洛方法。
在各种科学学科中,都有许多使用蒙特卡洛方法的例子。
例如,蒙特卡洛方法可用于
- 计算在复杂游戏中对手移动的概率。
- 计算未来天气事件的概率。
- 在特定条件下计算车辆碰撞的概率。
这些方法用于解决应用概率中的困难推理问题,例如从概率图模型中采样。
与此相关的是在贝叶斯模型中使用的序列蒙特卡洛方法,这些方法通常被称为粒子滤波器。
粒子滤波(PF)是一种基于蒙特卡洛或模拟的算法,用于递归贝叶斯推理。
— 第 823 页,《机器学习:概率视角》,2012 年。
蒙特卡洛方法在人工智能和机器学习中也很普遍。
实现机器学习目标的许多重要技术都基于从某个概率分布中抽取样本,并使用这些样本形成对某个所需量的蒙特卡洛估计。
— 第 590 页,《深度学习》,2016 年。
它们为通过模拟估计人工智能问题中的结果概率(例如机器人技术)奠定了基础。更简单地说,蒙特卡洛方法用于解决难以处理的积分问题,例如在计算机图形学的路径追踪中,在渲染计算机生成的场景时,发射随机光线。
在机器学习中,蒙特卡洛方法为重采样技术奠定了基础,例如用于估计模型准确性等量的自助法,该方法用于估计模型在有限数据集上的准确性。
自助法是一种简单的蒙特卡洛技术,用于近似采样分布。在估计量是真实参数的复杂函数的情况下,这尤其有用。
— 第 192 页,《机器学习:概率视角》,2012 年。
在调整模型时随机采样模型超参数是一种蒙特卡洛方法,集成模型也用于克服诸如小型数据集的有限大小和噪声以及学习算法的随机方差等挑战。
- 重采样算法。
- 随机超参数调整。
- 集成学习算法。
蒙特卡洛方法也为随机或随机优化算法奠定了基础,例如流行的模拟退火优化技术。
蒙特卡洛算法(模拟退火是其中一个例子)被广泛用于科学的许多分支,以估计难以精确计算的量。
— 第 530 页,《人工智能:现代方法》,第 3 版,2009 年。
- 随机优化算法。
蒙特卡洛采样工作示例
我们可以通过一个实际示例使蒙特卡洛采样具体化。
在这种情况下,我们将有一个定义随机变量概率分布的函数。我们将使用均值为 50、标准差为 5 的高斯分布,并从该分布中抽取随机样本。
让我们假设我们不知道该随机变量的概率分布的形式,并且我们想对该函数进行采样以了解概率密度。我们可以抽取一个给定大小的样本并绘制直方图来估计密度。
可以使用NumPy 的 normal() 函数从具有指定均值 (mu)、标准差 (sigma) 和样本大小的高斯分布中随机抽取样本。
为了使示例更有趣,我们将用不同大小的样本重复此实验四次。我们期望随着样本大小的增加,概率密度将更好地近似目标函数的真实密度,这符合大数定律。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
# 样本大小对蒙特卡洛样本影响的示例 from numpy.random import normal from matplotlib import pyplot # 定义分布 mu = 50 sigma = 5 # 生成不同大小的蒙特卡洛样本 sizes = [10, 50, 100, 1000] for i in range(len(sizes)): # 生成样本 sample = normal(mu, sigma, sizes[i]) # 绘制样本直方图 pyplot.subplot(2, 2, i+1) pyplot.hist(sample, bins=20) pyplot.title('%d samples' % sizes[i]) pyplot.xticks([]) # 显示绘图 pyplot.show() |
运行示例会创建四个不同大小的样本,并为每个样本绘制直方图。
我们可以看到,10 和 50 的小样本量未能有效捕捉目标函数的密度。我们可以看到 100 个样本效果更好,但直到 1,000 个样本,我们才清楚地看到高斯概率分布熟悉的钟形。
这突显了即使对于简单的随机变量,也需要抽取大量样本,以及样本数量增加带来的近似精度提高的好处。
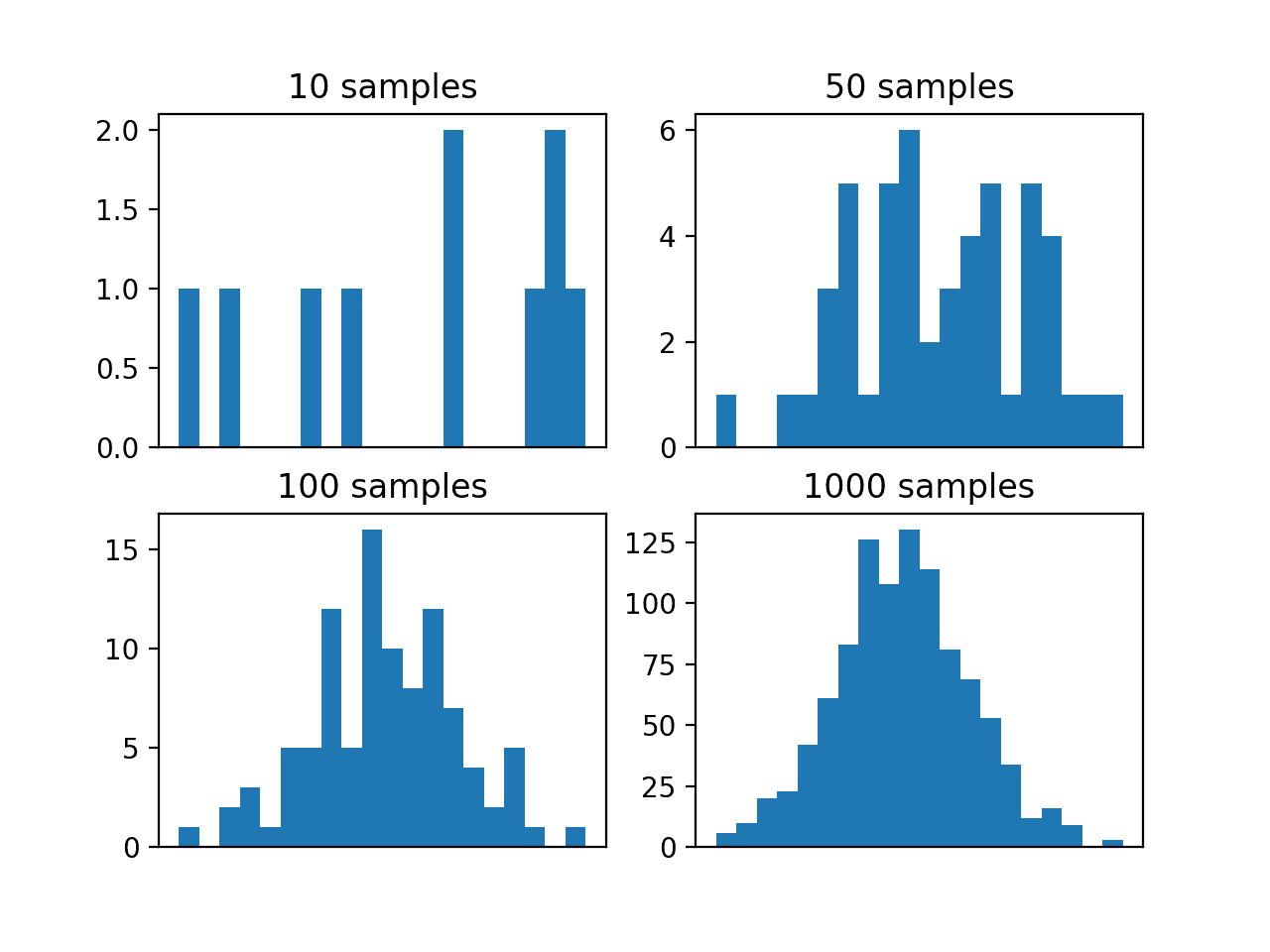
来自目标函数的不同大小的蒙特卡洛样本的直方图
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
书籍
- 第 29 章 蒙特卡洛方法,《信息论、推理与学习算法》,2003 年。
- 第 27 章 采样,《贝叶斯推理与机器学习》,2011 年。
- 第 14.5 节 贝叶斯网络的近似推理,《人工智能:现代方法》,第 3 版,2009 年。
- 第 23 章 蒙特卡洛推理,《机器学习:概率视角》,2012 年。
- 第 11 章 采样方法,《模式识别与机器学习》,2006 年。
- 第 17 章 蒙特卡洛方法,《深度学习》,2016 年。
文章
总结
在本文中,您了解了用于采样概率分布的蒙特卡洛方法。
具体来说,你学到了:
- 通常,我们无法计算概率中的所需量,但我们可以直接或间接定义随机变量的概率分布。
- 蒙特卡洛采样是用于从概率分布中随机采样的一类方法。
- 蒙特卡洛采样为许多机器学习方法提供了基础,例如重采样、超参数调整和集成学习。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。





我对参加这个速成课程很感兴趣,以便更好地理解使用 Python 进行概率和蒙特卡洛模拟。我的任务是为我的组织验证风险模型。通过这次验证,我希望更好地理解我所做的事情以及理解蒙特卡洛模拟的步骤。我拥有计算机科学学位,并且了解 R 和 Python。我购买了您的电子书,但实际上并没有完成任何作业,我需要一次“飞跃”来完成一项作业。我认为这就是我的“飞跃”。
坚持住,Gladys。
蒙特卡洛模拟的核心非常简单。它只是一个带有花哨名称的工具。
专注于它能教会你关于你特定模型的知识。
对学习者来说是伟大的作品。
谢谢!
尊敬的Jason博士
我需要做 MC 不确定性测试,看看 ANN 预测在“R”中的表现如何?
我的问题如下:
1) 对于 MC 模拟的随机采样:我应该从实际值或 ANN 模型预测的值中寻找 mu、sigma 等吗?
2) 如何决定样本量?以及每个大小的样本数,例如您在这里选择的 10、50、100、1000?
3) 最后,正如您所描述的,形状良好的分布图更适合报告,即解释良好的样本大小。在我看来,也需要为 ANN 建模相同的样本大小,以查看其预测兼容性?
如果我的问题让您感到困惑,请原谅。我的目标是使用 MC 来分析 ANN 预测性能的不确定性。
此致
Suraj
您正在预测误差中找到 mu 和 sigma。
也许保持较小以避免计算成本,例如 30。
您是否愿意分享更多关于您的方法?我正在做类似的事情,遇到了一些困难。
尊敬的Jason博士,
在上面的示例中,您为不同的样本大小模拟了正态分布。
我对此有个疑问。
虽然较小样本模拟的直方图形状与正态分布不相似,但是否存在统计检验来确定小样本集是否来自正态分布,例如使用 K-S 检验或 Shapiro-Wilks 检验,甚至使用熵?
我还有另一个关于蒙特卡洛模拟的问题。
我记得在本科课程中做过一个蒙特卡洛模拟练习。例如,从均匀分布生成 1000 个样本,并确定落在单位圆内的样本比例与生成的总点数之比。结果是 pi ≈ 3.141 的近似值。
这种蒙特卡洛模拟的应用是否在机器学习中使用?
谢谢你,
悉尼的Anthony
是的,其中一种检验。
https://machinelearning.org.cn/a-gentle-introduction-to-normality-tests-in-python/
是的,这是该方法近似一个量的绝佳用途。
尊敬的Jason博士,
我查阅了“Python 中的正态性检验入门”。
有使用 qqplot 的可视化检验和三个检验。
我从正态分布生成了大小为 50 和 20 的小样本。使用 qqplot,存在“对称性”,一半的值在“理论”检验的上方,一半的值在下方。
图形绘制并非视觉显示的全部。
正如您在检验方面所说,您建议进行所有三个数值统计检验。
供您参考,针对样本大小为 20 和 50 的统计检验表明,尽管数据在视觉上看起来不像正态分布,但所有数值检验(Shapiro-Wilk、Anderson 和 D’Agostino)均表明样本大小可能来自正态分布。所有 p 值都大于 alpha。
谢谢你,
悉尼的Anthony
干得漂亮!
嗨,Jason,
感谢您的帖子。
我对样本的值来自哪里感到有点困惑。
例如,假设我使用 RNN 训练了一个模型,并想预测第二天,基于最后 5 个观测值(例如 [10, 30, 50, 5, 4])。
使用类似泊松的似然性并创建蒙特卡洛迹的等效物,以便最终我可以计算例如输出分布的分位数或评估预测的不确定性。
在这种情况下,您可以拥有一个模型集成,每个模型都进行预测并对预测空间进行采样。
或者一个模型在输入中添加了微小的随机性,从而对预测空间进行采样。
我有一个关于多区域平板中子输运的问题,如果您有说明过程步骤的流程图或图,我正在尝试使用 Python 编程,但我无法做到。
抱歉,我没有。
尊敬的 Jason 博士
我正在尝试使用马尔可夫链蒙特卡洛(MCMC)进行纠缠交换,以实现长距离量子通信,您认为 MCMC 能否提高通信节点之间或通道的比特率
为了让问题更清晰,我引用一篇文章说:
“然而,量子中继器可实现的距离仍然
有限。原因在于,为了能够将纠缠从
对 A–B 和对 B–C 交换到 A–C,纠缠必须首先在
对 A–B 和 B–C 之间建立。然而,所有光子
在 A 和 B 之间以及在 B 和 C 之间的传播概率
与光子直接从 A 传播到 C 的概率完全相同。
因此,纠缠交换本身无望
增加比特率。”
谢谢你
我不知道,抱歉。
嗨,Jason,
非常感谢这个精彩的教程。我有一个问题。
如何对修改后的正态分布进行MC抽样,例如 f(x)*正态分布,其中f(x)可以是任何函数,例如x**2或其他?
非常感谢,
Ameir
为什么不直接对函数进行抽样?
如果这是一个问题,为什么不使用经验分布?
https://machinelearning.org.cn/empirical-distribution-function-in-python/
嗨,Jason,
非常感谢这个精彩的教程。我有一个问题。
假设我有一组数据和一个函数f(x)。使用这组数据,我绘制一个直方图。如果直方图表现良好,我可以大致估算出概率密度函数p(x),并用它来计算∫p(x)*f(x),这就是最终目标。
当直方图表现不好,并且我几乎无法估算出p(x)的PDF时,如何只给定数据和f(x)来数值计算∫p(x)*f(x)?
看这里
https://machinelearning.org.cn/empirical-distribution-function-in-python/
嗨,Jason,
非常感谢您的回复。我非常感激!
这个经验分布函数效果很好。但是,当涉及到积分(这是最终目标)时,我不知道该如何做。
假设我使用经验分布,我能够绘制出结果曲线。然后我如何获取该输出,将其乘以f(x)然后进行积分?
非常感谢,
Ameir
我认为你可以读出 individual values(例如P(x)或x对应P,但我认为它无法提供比这更高级的工具)。我建议查看API。
嗨,Jason,
这是一篇很棒的文章——非常清晰和信息丰富。但我想您可能想知道,这张照片是意大利的五渔村,而不是蒙特卡洛!
谢谢!
嗨,Jason,
感谢这篇简短的文章。我想总结一下我这几天阅读大量资料后学到的一些关于我正在尝试解决的问题的东西。假设我为两个输入参数设定了界限(最小值、最大值),但我对参数的底层分布一无所知。因此,根据我的理解,我会进行拟合优度检验来确认我对输入参数的假设,然后进行蒙特卡洛模拟。为了检查所需的迭代次数,我会在每次模拟后检查方差吗?还是有其他方法?
另外,抽样技术究竟在什么时候使用?
如何说明输出分布是我的模型的最佳选择?进行另一个拟合优度检验吗?
什么时候使用抽样技术、马尔可夫方法或粒子滤波方法?或者我如何排除使用不同方法解决我的模型这种可能性?
此外,使用不同的抽样技术是否也属于一种方法?
Faithfull Student
Biddappa
也许可以从一些非常简单的方法开始,比如在一个网格上对你的域进行抽样,然后绘制每个变量的图,以了解分布和关系。
如果我想选择哪种技术,有哪些与蒙特卡洛技术相比较的技术?
也许是其他的抽样算法
https://en.wikipedia.org/wiki/Markov_chain_Monte_Carlo
尊敬的Brownlee博士
你好,
如您所知,深度学习模型需要大量数据。如果某个区域/问题的数据有限,我能否通过一种技术(例如蒙特卡洛方法)来增加数据点(数据),然后使用深度学习?换句话说,在这种情况下,深度学习模型可靠吗?
在许多工程问题中,数据通常不足,因此深度学习的应用是一个挑战。
谢谢你的帮助。
您需要多少数据确实取决于您要解决的问题。一种技术是使用bootstrap方法来扩充数据集(请参阅https://machinelearning.org.cn/a-gentle-introduction-to-the-bootstrap-method/了解介绍)。对于图像处理任务,人们有各种各样的数据增强方法,例如稍微旋转图像、翻转图像、调整颜色等。您甚至可以考虑一种通过模拟生成数据的智能方法。希望这能激发您解决问题的思路。
请在上面的图片中注明,您发布的风景不是蒙特卡洛,而是意大利的五渔村。谢谢。
感谢您的反馈,Pierfranco!