使用 Python 实现多项逻辑回归

作者 Jason Brownlee 于 2020年9月1日发布在 Python 机器学习 28

多项逻辑回归是逻辑回归的扩展，它增加了对多类别分类问题的原生支持。

默认情况下，逻辑回归仅限于二元分类问题。像一对多这样的扩展可以允许逻辑回归用于多类别分类问题，尽管它们要求首先将分类问题转换为多个二元分类问题。

相反，多项逻辑回归算法是逻辑回归模型的扩展，它涉及将损失函数更改为交叉熵损失，并将概率分布预测为多项概率分布，以原生支持多类别分类问题。

在本教程中，您将了解如何在 Python 中开发多项逻辑回归模型。

完成本教程后，您将了解：

多项逻辑回归是逻辑回归的扩展，用于多类别分类。
如何开发和评估多项逻辑回归模型，并开发一个最终模型以在新数据上进行预测。
如何为多项逻辑回归模型调整正则化参数。

让我们开始吧。

Multinomial Logistic Regression With Python

使用 Python 实现多项逻辑回归
照片来源：Nicolas Rénac，部分权利保留。

教程概述

本教程分为三个部分；它们是：

多项逻辑回归
评估多项逻辑回归模型
为多项逻辑回归调整正则化

多项逻辑回归

逻辑回归是一种分类算法。

它适用于具有数值输入变量和具有两个值或类别的分类目标变量的数据集。这类问题被称为二元分类问题。

逻辑回归是为二元问题设计的，它使用二项概率分布函数来建模目标。类别标签被映射为：正类或结果为 1，负类或结果为 0。拟合的模型预测一个示例属于类别 1 的概率。

默认情况下，逻辑回归不能用于具有三个以上类别标签的分类任务，即多类别分类。

相反，它需要修改以支持多类别分类问题。

一种将逻辑回归应用于多类别分类问题的流行方法是将多类别分类问题拆分为多个二元分类问题，并在每个子问题上拟合标准逻辑回归模型。这类技术包括一对多和一对一的包装模型。

另一种方法是修改逻辑回归模型以直接支持预测多个类别标签。具体来说，是预测一个输入示例属于每个已知类别的概率。

定义多类别概率的概率分布称为多项概率分布。一个经过修改以学习和预测多项概率分布的逻辑回归模型称为多项逻辑回归。类似地，我们可以将默认或标准逻辑回归称为二项逻辑回归。

二项逻辑回归：标准逻辑回归，为每个输入示例预测二项概率（即两个类别）。
多项逻辑回归：逻辑回归的修改版本，为每个输入示例预测多项概率（即三个以上类别）。

如果您不熟悉二项和多项概率分布，您可能想阅读本教程

机器学习中的离散概率分布

将逻辑回归从二项概率改为多项概率需要更改用于训练模型的损失函数（例如，从对数损失到交叉熵损失），并更改输出，从单个概率值改为每个类别的概率。

现在我们熟悉了多项逻辑回归，让我们看看如何在 Python 中开发和评估多项逻辑回归模型。

评估多项逻辑回归模型

在本节中，我们将使用 scikit-learn Python 机器学习库来开发和评估多项逻辑回归模型。

首先，我们将定义一个合成的多类别分类数据集作为研究的基础。这是一个通用数据集，稍后您可以轻松替换为您自己的加载数据集。

可以使用 make_classification() 函数生成具有给定行数、列数和类别数的数据集。在这种情况下，我们将生成一个包含 1,000 行、10 个输入变量或列和 3 个类别的数据集。

下面的示例生成数据集，并总结数组的形状以及三个类别中示例的分布。

# test classification dataset
from collections import Counter
from sklearn.datasets import make_classification
# define dataset
X, y = make_classification(n_samples=1000, n_features=10, n_informative=5, n_redundant=5, n_classes=3, random_state=1)
# summarize the dataset
print(X.shape, y.shape)
print(Counter(y))

# 测试分类数据集

from collections import Counter

from sklearn.datasets import make_classification

# 定义数据集

X, y = make_classification(n_samples=1000, n_features=10, n_informative=5, n_redundant=5, n_classes=3, random_state=1)

# 汇总数据集

print(X.shape, y.shape)

print(Counter(y))

运行示例确认数据集有 1,000 行和 10 列，正如我们预期的那样，并且这些行大致均匀地分布在三个类别中，每个类别约有 334 个示例。

(1000, 10) (1000,)
Counter({1: 334, 2: 334, 0: 332})

1 2	(1000, 10) (1000,) Counter({1: 334, 2: 334, 0: 332})

scikit-learn 库通过 LogisticRegression 类支持逻辑回归。

可以通过将“multi_class”参数设置为“multinomial”并将“solver”参数设置为支持多项逻辑回归的求解器，例如“lbfgs”，来为多项逻辑回归配置 LogisticRegression 类。

...
# define the multinomial logistic regression model
model = LogisticRegression(multi_class='multinomial', solver='lbfgs')

...

# 定义多项逻辑回归模型

model = LogisticRegression(multi_class='multinomial', solver='lbfgs')

多项逻辑回归模型将使用交叉熵损失进行拟合，并将为每个整数编码的类别标签预测整数值。

现在我们熟悉了多项逻辑回归 API，我们可以看看如何在合成的多类别分类数据集上评估多项逻辑回归模型。

使用重复分层 k 折交叉验证来评估分类模型是一个好习惯。分层可确保每个交叉验证折叠都具有与整个训练数据集相同的示例类别分布。

我们将使用三次重复和 10 折，这是一个不错的默认设置，并使用分类准确率来评估模型性能，因为类别是平衡的。

下面列出了评估多项逻辑回归用于多类别分类的完整示例。

# evaluate multinomial logistic regression model
from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.linear_model import LogisticRegression
# define dataset
X, y = make_classification(n_samples=1000, n_features=10, n_informative=5, n_redundant=5, n_classes=3, random_state=1)
# define the multinomial logistic regression model
model = LogisticRegression(multi_class='multinomial', solver='lbfgs')
# define the model evaluation procedure
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
# evaluate the model and collect the scores
n_scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1)
# report the model performance
print('Mean Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores)))

# 评估多项逻辑回归模型

from numpy import mean

from numpy import std

from sklearn.datasets import make_classification

from sklearn.model_selection import cross_val_score

from sklearn.model_selection import RepeatedStratifiedKFold

从 sklearn.线性模型导入 LogisticRegression

# 定义数据集

X, y = make_classification(n_samples=1000, n_features=10, n_informative=5, n_redundant=5, n_classes=3, random_state=1)

# 定义多项逻辑回归模型

model = LogisticRegression(multi_class='multinomial', solver='lbfgs')

# 定义模型评估程序

cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)

# 评估模型并收集分数

n_scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1)

# 报告模型性能

print('平均准确率: %.3f (%.3f)' % (mean(n_scores), std(n_scores)))

运行示例报告了评估过程所有折叠和重复的平均分类准确率。

注意：由于算法或评估过程的随机性，或者数值精度的差异，您的结果可能有所不同。考虑运行示例几次并比较平均结果。

在这种情况下，我们可以看到，在我们的合成分类数据集上，具有默认正则化参数的多项逻辑回归模型达到了约 68.1% 的平均分类准确率。

Mean Accuracy: 0.681 (0.042)

1	平均准确率: 0.681 (0.042)

我们可以决定使用多项逻辑回归模型作为最终模型，并在新数据上进行预测。

这可以通过首先在所有可用数据上拟合模型，然后调用 predict() 函数来为新数据进行预测来实现。

下面的示例演示了如何使用多项逻辑回归模型对新数据进行预测。

# make a prediction with a multinomial logistic regression model
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
# define dataset
X, y = make_classification(n_samples=1000, n_features=10, n_informative=5, n_redundant=5, n_classes=3, random_state=1)
# define the multinomial logistic regression model
model = LogisticRegression(multi_class='multinomial', solver='lbfgs')
# fit the model on the whole dataset
model.fit(X, y)
# define a single row of input data
row = [1.89149379, -0.39847585, 1.63856893, 0.01647165, 1.51892395, -3.52651223, 1.80998823, 0.58810926, -0.02542177, -0.52835426]
# predict the class label
yhat = model.predict([row])
# summarize the predicted class
print('Predicted Class: %d' % yhat[0])

# 使用多项逻辑回归模型进行预测

from sklearn.datasets import make_classification

从 sklearn.线性模型导入 LogisticRegression

# 定义数据集

X, y = make_classification(n_samples=1000, n_features=10, n_informative=5, n_redundant=5, n_classes=3, random_state=1)

# 定义多项逻辑回归模型

model = LogisticRegression(multi_class='multinomial', solver='lbfgs')

# 在整个数据集上拟合模型

model.fit(X, y)

# 定义单行输入数据

row = [1.89149379, -0.39847585, 1.63856893, 0.01647165, 1.51892395, -3.52651223, 1.80998823, 0.58810926, -0.02542177, -0.52835426]

# 预测类别标签

yhat = model.predict([row])

# 总结预测的类别

print('预测类别: %d' % yhat[0])

运行示例首先在所有可用数据上拟合模型，然后定义一行数据，该数据提供给模型以进行预测。

在这种情况下，我们可以看到模型为单行数据预测了类别“1”。

Predicted Class: 1

预测类别：1

多项逻辑回归的一个优点是它可以预测数据集中所有已知类别的校准概率。

这可以通过调用模型上的 predict_proba() 函数来实现。

下面的示例演示了如何使用多项逻辑回归模型为新示例预测多项概率分布。

# predict probabilities with a multinomial logistic regression model
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
# define dataset
X, y = make_classification(n_samples=1000, n_features=10, n_informative=5, n_redundant=5, n_classes=3, random_state=1)
# define the multinomial logistic regression model
model = LogisticRegression(multi_class='multinomial', solver='lbfgs')
# fit the model on the whole dataset
model.fit(X, y)
# define a single row of input data
row = [1.89149379, -0.39847585, 1.63856893, 0.01647165, 1.51892395, -3.52651223, 1.80998823, 0.58810926, -0.02542177, -0.52835426]
# predict a multinomial probability distribution
yhat = model.predict_proba([row])
# summarize the predicted probabilities
print('Predicted Probabilities: %s' % yhat[0])

# 使用多项逻辑回归模型预测概率

from sklearn.datasets import make_classification

从 sklearn.线性模型导入 LogisticRegression

# 定义数据集

X, y = make_classification(n_samples=1000, n_features=10, n_informative=5, n_redundant=5, n_classes=3, random_state=1)

# 定义多项逻辑回归模型

model = LogisticRegression(multi_class='multinomial', solver='lbfgs')

# 在整个数据集上拟合模型

model.fit(X, y)

# 定义单行输入数据

row = [1.89149379, -0.39847585, 1.63856893, 0.01647165, 1.51892395, -3.52651223, 1.80998823, 0.58810926, -0.02542177, -0.52835426]

# 预测多项概率分布

yhat = model.predict_proba([row])

# 总结预测的概率

print('预测概率: %s' % yhat[0])

运行示例首先在所有可用数据上拟合模型，然后定义一行数据，该数据提供给模型以预测类别概率。

注意：由于算法或评估过程的随机性，或者数值精度的差异，您的结果可能有所不同。考虑运行示例几次并比较平均结果。

在这种情况下，我们可以看到类别 1（例如，数组索引映射到类别整数值）具有最大的预测概率，约为 0.50。

Predicted Probabilities: [0.16470456 0.50297138 0.33232406]

1	预测概率: [0.16470456 0.50297138 0.33232406]

现在我们熟悉了评估和使用多项逻辑回归模型，让我们探讨如何调整模型超参数。

为多项逻辑回归调整正则化

多项逻辑回归的一个重要超参数是正则化项。

该项对模型施加压力，促使其寻找更小的模型权重。这是通过将模型系数的加权和添加到损失函数来实现的，鼓励模型在拟合模型的同时减小权重的尺寸。

一种流行的正则化类型是 L2 正则化，它将（加权的）系数平方和添加到损失函数中。可以使用系数的加权来减小正则化的强度，从完全正则化到非常轻微的正则化。

默认情况下，LogisticRegression 类使用 L2 正则化，系数加权设置为 1.0。可以通过“penalty”参数设置正则化类型，值为“l1”、“l2”、“elasticnet”（例如，两者都有），但并非所有求解器都支持所有正则化类型。“C”参数用于设置系数的加权。

...
# define the multinomial logistic regression model with a default penalty
LogisticRegression(multi_class='multinomial', solver='lbfgs', penalty='l2', C=1.0)

...

# 定义具有默认正则化参数的多项逻辑回归模型

LogisticRegression(multi_class='multinomial', solver='lbfgs', penalty='l2', C=1.0)

正则化的加权实际上是反向加权，也许正则化 = 1 – C。

根据文档

C : float, default=1.0
正则化强度的倒数；必须是正浮点数。与支持向量机一样，较小的值表示较强的正则化。

这意味着接近 1.0 的值表示非常轻微的正则化，而接近零的值表示强正则化。C 值为 1.0 可能表示没有正则化。

C 接近 1.0：轻微正则化。
C 接近 0.0：强正则化。

可以通过将“penalty”参数设置为字符串“none”来禁用正则化。

...
# define the multinomial logistic regression model without a penalty
LogisticRegression(multi_class='multinomial', solver='lbfgs', penalty='none')

...

# 定义不带正则化参数的多项逻辑回归模型

LogisticRegression(multi_class='multinomial', solver='lbfgs', penalty='none')

现在我们熟悉了正则化，让我们看看如何探索不同正则化值对多项逻辑回归模型性能的影响。

通常在对数尺度上测试正则化值，以快速发现适合模型的正则化尺度。一旦找到，在该尺度上进一步调整可能是有益的。

我们将探索 L2 正则化，其加权值范围从 0.0001 到 1.0（在对数尺度上），以及无正则化或 0.0。

下面列出了评估多项逻辑回归的 L2 正则化值完整示例。

# tune regularization for multinomial logistic regression
from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.linear_model import LogisticRegression
from matplotlib import pyplot

# get the dataset
def get_dataset():
	X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=1, n_classes=3)
	return X, y

# get a list of models to evaluate
def get_models():
	models = dict()
	for p in [0.0, 0.0001, 0.001, 0.01, 0.1, 1.0]:
		# create name for model
		key = '%.4f' % p
		# turn off penalty in some cases
		if p == 0.0:
			# no penalty in this case
			models[key] = LogisticRegression(multi_class='multinomial', solver='lbfgs', penalty='none')
		else:
			models[key] = LogisticRegression(multi_class='multinomial', solver='lbfgs', penalty='l2', C=p)
	return models

# evaluate a give model using cross-validation
def evaluate_model(model, X, y):
	# define the evaluation procedure
	cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
	# evaluate the model
	scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1)
	return scores

# define dataset
X, y = get_dataset()
# get the models to evaluate
models = get_models()
# evaluate the models and store results
results, names = list(), list()
for name, model in models.items():
	# evaluate the model and collect the scores
	scores = evaluate_model(model, X, y)
	# store the results
	results.append(scores)
	names.append(name)
	# summarize progress along the way
	print('>%s %.3f (%.3f)' % (name, mean(scores), std(scores)))
# plot model performance for comparison
pyplot.boxplot(results, labels=names, showmeans=True)
pyplot.show()

# 调整多项逻辑回归的正则化

from numpy import mean

from numpy import std

from sklearn.datasets import make_classification

from sklearn.model_selection import cross_val_score

from sklearn.model_selection import RepeatedStratifiedKFold

from sklearn.linear_model import LogisticRegression

from matplotlib import pyplot

# 获取数据集

定义获取_数据集():

X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=1, n_classes=3)

返回 X, y

# 获取要评估的模型列表

定义获取_模型():

models = dict()

for p in [0.0, 0.0001, 0.001, 0.01, 0.1, 1.0]:

# 创建模型名称

key = '%.4f' % p

# 在某些情况下关闭正则化

if p == 0.0:

# 在这种情况下没有正则化

models[key] = LogisticRegression(multi_class='multinomial', solver='lbfgs', penalty='none')

else:

models[key] = LogisticRegression(multi_class='multinomial', solver='lbfgs', penalty='l2', C=p)

返回模型

# 使用交叉验证评估给定模型

def evaluate_model(model, X, y):

# 定义评估过程

cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)

# 评估模型

scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1)

返回分数

# 定义数据集

X, y = get_dataset()

# 获取要评估的模型

模型 = 获取_模型()

# 评估模型并存储结果

results, names = list(), list()

for name, model in models.items():

# 评估模型并收集分数

scores = evaluate_model(model, X, y)

# 存储结果

results.append(scores)

names.append(name)

# 边进行边总结进展

print('>%s %.3f (%.3f)' % (name, mean(scores), std(scores)))

# 绘制模型性能以供比较

pyplot.boxplot(results, labels=names, showmeans=True)

pyplot.show()

运行示例会报告沿途每个配置的平均分类准确率。

注意：由于算法或评估过程的随机性，或者数值精度的差异，您的结果可能有所不同。考虑运行示例几次并比较平均结果。

在这种情况下，我们可以看到 C 值为 1.0 获得了最佳分数，约为 77.7%，这与使用不带正则化（获得相同分数）相同。

>0.0000 0.777 (0.037)
>0.0001 0.683 (0.049)
>0.0010 0.762 (0.044)
>0.0100 0.775 (0.040)
>0.1000 0.774 (0.038)
>1.0000 0.777 (0.037)

>0.0000 0.777 (0.037)

>0.0001 0.683 (0.049)

>0.0010 0.762 (0.044)

>0.0100 0.775 (0.040)

>0.1000 0.774 (0.038)

>1.0000 0.777 (0.037)

为每个配置的准确率分数创建了箱须图，并且所有图都并排显示在同一比例的图形上以便进行直接比较。

在这种情况下，我们可以看到，在该数据集上使用的正则化越大（即 C 值越小），模型的性能就越差。

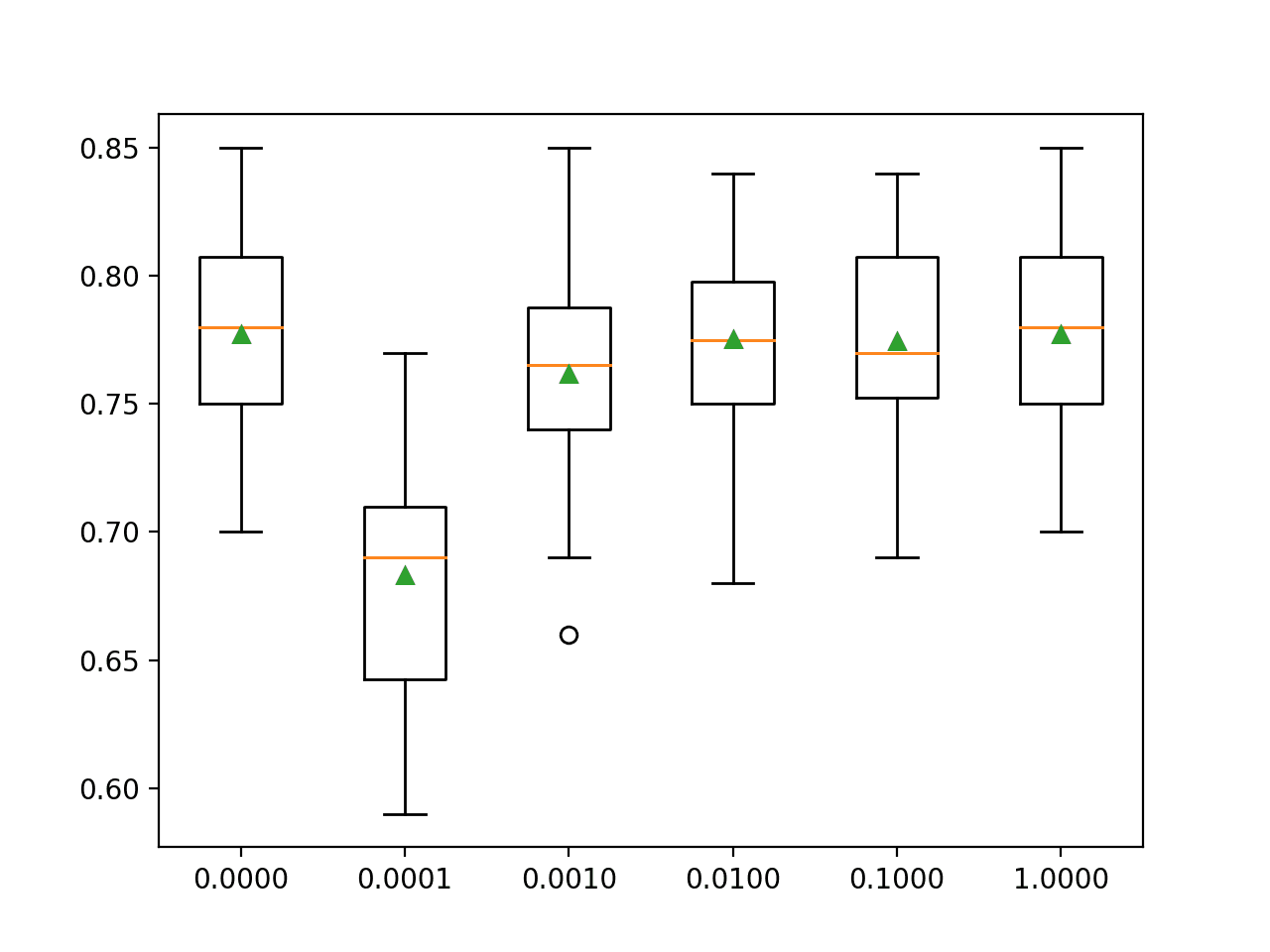
Box and Whisker Plots of L2 Penalty Configuration vs. Accuracy for Multinomial Logistic Regression

多项逻辑回归的 L2 正则化配置与准确率的箱须图

进一步阅读

如果您想深入了解，本节提供了更多关于该主题的资源。

API

文章

总结

在本教程中，您了解了如何在 Python 中开发多项逻辑回归模型。

具体来说，你学到了：

多项逻辑回归是逻辑回归的扩展，用于多类别分类。
如何开发和评估多项逻辑回归模型，并开发一个最终模型以在新数据上进行预测。
如何为多项逻辑回归模型调整正则化参数。

你有什么问题吗？
在下面的评论中提出你的问题，我会尽力回答。

关于此主题的更多信息

半监督学习与标签传播

对《使用 Python 进行多项逻辑回归》的 28 条回复

Marry 2021年1月2日下午11:39 #

嗨，Jason，
非常感谢您提供的信息丰富且极具教育意义的博客。我从您的网站学到了很多。
我正在处理一个具有有序目标变量的机器学习项目。
1- 我应该将其视为分类还是回归问题？
2- 如果是回归，用哪种回归算法？
3- 如果是分类，我可以使用多项逻辑回归来处理有序目标吗？

回复
- Jason Brownlee 2021年1月2日下午12:06 #
  
  不客气。
  
  您可以尝试将其建模为分类和回归，看看哪种效果最好。
  
  尝试一套算法并找出最适合您的算法。
  
  回复
Marry 2021年1月2日下午12:18 #

感谢您迅速回复。抱歉，我是机器学习新手；我对回归部分有些困惑。这是否意味着我可以尝试任何回归算法，而不管目标变量的非连续性质，它是有序的（1-10）？

回复
- Jason Brownlee 2021年1月3日上午5:51 #
  
  是的，虽然您可能想“解释”预测，例如四舍五入到整数并计算对您的项目有意义的指标。
  
  回复
sukhpal 2021年1月2日下午11:05 #

先生，我们如何进一步提高已优化模型的决策能力？

回复
- Jason Brownlee 2021年1月3日上午5:55 #
  
  将预测与其他模型结合，称为集成。
  
  回复
marco 2021年1月2日下午11:52 #

你好 Jason，
是否所有 scikit-learn 和 Xgbost 估计器都需要数据集进行归一化/标准化？
也就是说，是否存在允许输入原始数据的估计器？
谢谢，
Marco

回复
- Jason Brownlee 2021年1月3日上午5:56 #
  
  不行。
  
  树可以处理原始数据。
  
  回复
marco 2021年1月2日下午11:53 #

Jason，
哪些估计器适用于不平衡数据集？
随机森林是否适用于医疗保健领域的预测，而这些领域的数据集通常是不平衡的？
谢谢，
Marco

回复
- Jason Brownlee 2021年1月3日上午5:57 #
  
  大多数可以直接使用，有些可以修改为成本敏感版本。
  
  从这里开始
  https://machinelearning.org.cn/start-here/#imbalanced
  
  回复
Albert 2021年3月14日上午1:48 #

你好 Jason，

感谢您提供的信息材料。

我一直在处理具有多个类别的多类数据集，如上面的示例，但我发现，如果不使用 OneVsRest 方法，就很难绘制 RoC 曲线并计算精度、召回率等。

我能否仅使用多项类别来绘制 ROC 曲线并计算其余指标？

提前感谢

Albert

回复
- Jason Brownlee 2021年3月14日上午5:28 #
  
  也许这可以作为第一步
  https://machinelearning.org.cn/roc-curves-and-precision-recall-curves-for-classification-in-python/
  
  回复
- Simon 2021年3月19日上午3:54 #
  
  我想知道您是否对此有了任何好的答案？我处境相同，我很难理解多项正态情况下 ROC 曲线的阈值应该是多少。
  
  回复
Oladiran Olanrewaju 2021年5月10日上午5:01 #

万一我想用 Python 生成多项数据。请解释一下步骤

回复
- Jason Brownlee 2021年5月10日上午6:22 #
  
  也许你可以使用make_classification()
  https://scikit-learn.cn/stable/modules/generated/sklearn.datasets.make_classification.html
  
  回复
Rusty 2021年11月3日上午4:21 #

嗨，Jason，

感谢这篇关于机器学习的富有启发性的博客。
我有一个问题：当你使用RepeatedStratifiedKFold来评估模型并从中获取分数时，但对于预测新数据，在这些模型批次中（如果n_splits=10，n_repeats=3，那将是30个模型，对吗？），应该选择哪个模型来应用？

再次感谢！

回复
- Adrian Tam 2021年11月7日上午7:23 #
  
  为了正确使用，不应该选择这些模型中的任何一个。K-fold是为了帮助你评估模型设计。一旦你完成了它，你应该用你完整的训练集重新训练模型。请参阅 https://machinelearning.org.cn/training-validation-test-split-and-cross-validation-done-right/
  
  回复
Luke 2022年5月25日下午1:55 #

感谢这篇文章，我对多项逻辑回归有一个问题。如果我想获得赛马中每匹马的获胜概率，如果数据集中的每一行都有参赛马匹的先验平均速度，我将如何区分第一场比赛（第一行）中的horse_1_speed与第二场比赛（第二行）中的horse_1_speed不同，因为实际上我可以将该比赛中的任何一匹马指定为horse_1？

回复
- James Carmichael 2022年5月26日上午1:58 #
  
  你好Luke…请缩小你的查询范围或用机器学习概念来重新表述，以便我们更好地帮助你。
  
  回复
Carol 2022年6月11日上午3:14 #

当我使用多项逻辑回归时，我仍然使用sigmoid函数吗？因为如果我有2个类别，我可以用sigmoid函数计算。那么对于3个或更多类别，我该如何使用这个函数？

回复
- James Carmichael 2022年6月11日上午9:20 #
  
  你好Carol…以下内容可能对你有帮助
  
  https://towardsdatascience.com/multivariate-logistic-regression-in-python-7c6255a286ec
  
  回复
skan 2023年1月11日上午6:41 #

如果我想拟合几个逻辑模型…我需要每次都实例化它们吗？
mymodel1 = LogisticRegression()
mymodel1.fit()
mymodel2 = LogisticRegression()
mymodel2.fit()
…

回复
Gabriel 2023年2月25日上午9:01 #

我如何知道我的数据的分布类型？我有一个包含分类值的数据库，并且所有属性（输入和输出）都有很多类别。您能告诉我哪种算法是分类新值的可行方法吗？

回复
- James Carmichael 2023年2月25日上午10:13 #
  
  你好Gabriel…以下资源可能对你有帮助
  
  https://machinelearning.org.cn/statistical-data-distributions/
  
  回复
Devon 2023年3月21日上午4:47 #

你好，感谢这个教程！我一直在尝试提取多项逻辑回归的系数，我跟着这个例子做的。我需要解释一个模型——我没有使用这种方法来分类数据。我使用了model.coef_来提取系数，但发现有些地方令人困惑，想知道您是否能提供一些澄清/指出正确的方向。

作为参考，我有四个类别和11个特征。我的系数矩阵是4x11（四行十一列）。

(1) 通常，对于多项逻辑回归，有一个结果是基础结果。（因此回归模型应该是具有三行十一列的矩阵）。有没有办法将其中一个类别设为基础结果？

(2) 我是否只需假设系数的顺序与特征数据相同？

看起来sklearn在提取模型信息方面并不特别适合。您是否推荐R或Python中的其他包用于此目的？

回复
- James Carmichael 2023年3月21日上午10:14 #
  
  你好Devon…我来尝试理解你的问题。请澄清你的model.coef_结果中令你困惑的地方？
  
  回复
  - raf1 2023年6月23日下午12:18 #
    
    在mlogit中应该有一个参考类别，对吗？它的系数应该为0。但是当我使用这段代码时，我发现所有类别的系数都不等于0。这是怎么回事？当我需要5个类别时，我应该得到4个系数，但这里我得到了全部5个
    
    回复
    - James Carmichael 2023年6月24日上午11:09 #
      
      你好raf1…你是复制粘贴的代码还是自己输入的？这里有一些额外的例子，希望能增加一些清晰度
      
      https://www.kaggle.com/code/saurabhbagchi/multinomial-logistic-regression-for-beginners
      
      回复

导航

使用 Python 实现多项逻辑回归

教程概述

多项逻辑回归

评估多项逻辑回归模型

为多项逻辑回归调整正则化

进一步阅读

相关教程

API

文章

总结

发现 Python 中的快速机器学习！

在几分钟内开发您自己的模型

最终将机器学习带入
您自己的项目

关于此主题的更多信息

对《使用 Python 进行多项逻辑回归》的 28 条回复

发表回复点击此处取消回复。

导航

教程概述

多项逻辑回归

评估多项逻辑回归模型

为多项逻辑回归调整正则化

进一步阅读

相关教程

API

文章

总结

发现 Python 中的快速机器学习！

在几分钟内开发您自己的模型

最终将机器学习带入您自己的项目

关于此主题的更多信息

对《使用 Python 进行多项逻辑回归》的 28 条回复

发表回复 点击此处取消回复。

最终将机器学习带入
您自己的项目

发表回复点击此处取消回复。