朴素贝叶斯是一种非常简单的分类算法,它对每个输入变量的独立性做出了强有力的假设。
尽管如此,它在大量的领域中已被证明是有效的。在本帖中,您将了解朴素贝叶斯算法在分类数据中的应用。阅读本帖后,您将了解:
- 如何处理朴素贝叶斯中的分类数据。
- 如何为朴素贝叶斯模型准备类别和条件概率。
- 如何使用学习到的朴素贝叶斯模型进行预测。
本帖是为开发者编写的,不假设您具有统计学或概率论背景。请打开电子表格,跟随一起学习。如果您对朴素贝叶斯有任何疑问,请在评论区提问,我将尽力回答。
用我的新书《精通机器学习算法》快速启动您的项目,书中包含分步教程和所有示例的Excel电子表格文件。
让我们开始吧。

机器学习朴素贝叶斯教程
照片作者:Beshef,部分权利保留。
教程数据集
该数据集是人为构造的。它描述了两个分类输入变量和一个具有两个输出的类别变量。
|
1 2 3 4 5 6 7 8 9 10 11 |
天气 汽车 类别 晴天 工作 出行 雨天 坏了 出行 晴天 工作 出行 晴天 工作 出行 晴天 工作 出行 雨天 坏了 在家 雨天 坏了 在家 晴天 工作 在家 晴天 坏了 在家 雨天 坏了 在家 |
我们可以将这些数据转换为数字。每个输入只有两个值,输出类别变量也有两个值。我们可以将每个变量转换为二进制,如下所示:
变量:天气
- 晴天 = 1
- 雨天 = 0
变量:汽车
- 工作 = 1
- 坏了 = 0
变量:类别
- 出行 = 1
- 在家 = 0
因此,我们可以重述数据集如下:
|
1 2 3 4 5 6 7 8 9 10 11 |
天气 汽车 类别 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 1 1 0 1 0 0 0 0 0 |
这可以使数据在电子表格或代码中更容易处理,如果您正在跟随操作的话。
获取您的免费算法思维导图
方便的机器学习算法思维导图样本。
我创建了一份方便的思维导图,其中包含60多种按类型组织的算法。
下载、打印并使用它。
还可以独家访问机器学习算法电子邮件迷你课程。
学习朴素贝叶斯模型
朴素贝叶斯模型需要从数据集中计算两种类型的数量:
- 类别概率。
- 条件概率。
让我们从类别概率开始。
计算类别概率
这是一个二分类问题,而且由于我们是人为构造的数据集,所以我们已经知道了每个类别的概率。
尽管如此,我们仍然可以计算类别0和类别1的类别概率,如下所示:
- P(类别=1) = count(类别=1) / (count(类别=0) + count(类别=1))
- P(类别=0) = count(类别=0) / (count(类别=0) + count(类别=1))
或者
- P(类别=1) = 5 / (5 + 5)
- P(类别=0) = 5 / (5 + 5)
计算结果是,任何数据实例属于类别0或类别1的概率都是0.5。
计算条件概率
条件概率是每个输入值给定每个类别值的概率。
该数据集的条件概率可以计算如下:
天气输入变量
- P(天气=晴天|类别=出行) = count(天气=晴天 and 类别=出行) / count(类别=出行)
- P(天气=雨天|类别=出行) = count(天气=雨天 and 类别=出行) / count(类别=出行)
- P(天气=晴天|类别=在家) = count(天气=晴天 and 类别=在家) / count(类别=在家)
- P(天气=雨天|类别=在家) = count(天气=雨天 and 类别=在家) / count(类别=在家)
代入数值,我们得到:
- P(天气=晴天|类别=出行) = 0.8
- P(天气=雨天|类别=出行) = 0.2
- P(天气=晴天|类别=在家) = 0.4
- P(天气=雨天|类别=在家) = 0.6
汽车输入变量
- P(汽车=工作|类别=出行) = count(汽车=工作 and 类别=出行) / count(类别=出行)
- P(汽车=坏了|类别=出行) = count(汽车=坏了 and 类别=出行) / count(类别=出行)
- P(汽车=工作|类别=在家) = count(汽车=工作 and 类别=在家) / count(类别=在家)
- P(汽车=坏了|类别=在家) = count(汽车=坏了 and 类别=在家) / count(类别=在家)
代入数值,我们得到:
- P(汽车=工作|类别=出行) = 0.8
- P(汽车=坏了|类别=出行) = 0.2
- P(汽车=工作|类别=在家) = 0.2
- P(汽车=坏了|类别=在家) = 0.8
现在我们有了使用朴素贝叶斯模型进行预测所需的一切。
用朴素贝叶斯进行预测
我们可以使用贝叶斯定理进行预测。
P(h|d) = (P(d|h) * P(h)) / P(d)
其中
- P(h|d) 是在数据d给定下假设h为真的概率。这被称为后验概率。
- P(d|h) 是在假设h为真情况下数据d的概率。
- P(h) 是假设h为真的概率(不考虑数据)。这被称为h的先验概率。
- P(d) 是数据的概率(不考虑假设)。
事实上,我们不需要概率来预测新数据实例最可能的类别。我们只需要分子以及产生最大响应的类别,这将是预测的输出。
MAP(h) = max(P(d|h) * P(h))
让我们用数据集中的第一个记录,并使用我们学习到的模型来预测它所属的类别。
天气=晴天,汽车=工作
我们将模型中这两种类别的概率代入并计算响应。从“出行”输出的响应开始。我们将条件概率相乘,然后乘以任何实例属于该类别的概率。
- 出行 = P(天气=晴天|类别=出行) * P(汽车=工作|类别=出行) * P(类别=出行)
- 出行 = 0.8 * 0.8 * 0.5
- 出行 = 0.32
我们可以对在家的情况进行相同的计算:
- 在家 = P(天气=晴天|类别=在家) * P(汽车=工作|类别=在家) * P(类别=在家)
- 在家 = 0.4 * 0.2 * 0.5
- 在家 = 0.04
我们可以看到0.32大于0.04,因此我们预测此实例为“出行”,这是正确的。
我们可以对整个数据集重复此操作,如下所示:
|
1 2 3 4 5 6 7 8 9 10 11 |
天气 汽车 类别 出行? 在家? 预测 晴天 工作 出行 0.32 0.04 出行 雨天 坏了 出行 0.02 0.24 在家 晴天 工作 出行 0.32 0.04 出行 晴天 工作 出行 0.32 0.04 出行 晴天 工作 出行 0.32 0.04 出行 雨天 坏了 在家 0.02 0.24 在家 雨天 坏了 在家 0.02 0.24 在家 晴天 工作 在家 0.32 0.04 出行 晴天 坏了 在家 0.08 0.16 在家 雨天 坏了 在家 0.02 0.24 在家 |
如果我们统计预测值与实际类别值的比较,我们可以获得80%的准确率,考虑到数据集中存在冲突的例子,这是一个很好的结果。
总结
在本帖中,您将了解如何从零开始实现朴素贝叶斯。您学到了:
- 如何使用朴素贝叶斯处理分类数据。
- 如何从训练数据中计算类别概率。
- 如何从训练数据中计算条件概率。
- 如何使用学习到的朴素贝叶斯模型对新数据进行预测。
您对朴素贝叶斯或本帖有任何疑问吗?
留下评论提问,我将尽力回答。



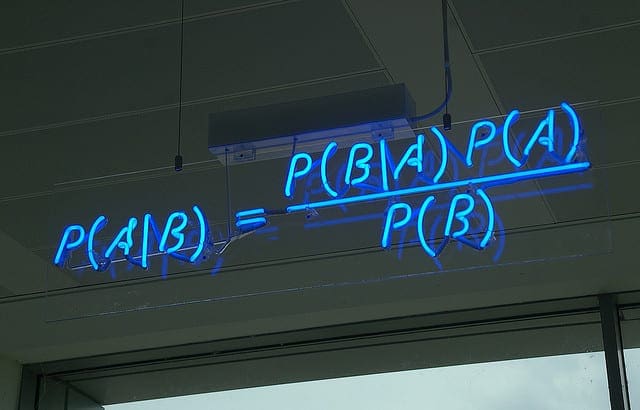


您真的应该在您的博客中添加MathJax来正确显示数学公式。
您可能是对的,但是不使用清晰的公式可能会让开发者觉得不那么令人生畏。
Jason您好,我很高兴您的文章对初学者来说如此易于理解!这篇写得非常清晰简单,谢谢!
我想知道这个朴素贝叶斯分类器如何用于“预测”?例如,您原始的数据集中不包含以下组合:
– 天气=雨天
– 汽车=工作。
您如何使用该模型来预测给定这两个输入时每个类别的概率?
谢谢Ben,
帖子里标题为“用朴素贝叶斯进行预测”的部分解释了如何根据新观察进行预测。
您的代码出现了这些错误:
File “C:\Users\Eng Adebayo\Documents\pybrain-master\naive-bayes.py”, line 103, in
main()
File “C:\Users\Eng Adebayo\Documents\pybrain-master\naive-bayes.py”, line 93, in main
dataset = loadCsv(filename)
File “C:\Users\Eng Adebayo\Documents\pybrain-master\naive-bayes.py”, line 12, in loadCsv
dataset[i] = [float(x) for x in dataset[i]]
File “C:\Users\Eng Adebayo\Documents\pybrain-master\naive-bayes.py”, line 12, in
dataset[i] = [float(x) for x in dataset[i]]
ValueError: 无法将字符串转换为浮点数
>>>
你好,
我在算法思维导图中找不到SVM!它属于哪个类别?
非常感谢!
也许是基于实例的方法?
您好,这篇文章非常棒,特别是对于我这样数学不太好的人来说(维基百科上的内容看起来比这里要难得多),但也许我理解错了,但条件概率是否正确?
P(天气=晴天|类别=出行) = count(天气=晴天 and 类别=出行) / count(类别=出行)
让我们举个另一个例子。假设输入是职业,输出是内向/外向。假设我采访100个人,询问他们的职业以及他们是内向还是外向。
现在,假设我只遇到3个IT工作者,而且他们都是内向的。其余97人也是其他职业且内向(仅为简化起见)。
现在,如果我按照您的例子,那么IT工作者是内向者的概率是:
P(职业=IT|类别=内向) = count(职业=IT=内向) / count(类别=内向)
也就是说:
3 / 100 = 3% 的IT工作者是内向的。但这是否正确?我们采访了3个IT人员,所有人都说是。难道不应该是:
P(职业=IT|类别=内向) = count(职业=IT=内向) / count(职业=IT)?
这样我们就得到了100%,这反映了我们的样本。或者?也许天气样本也类似?
并且应该是:
P(天气=晴天|类别=出行) = count(天气=晴天 and 类别=出行) / count(天气=晴天)?
Luky 敬上
也许两种比例都有意义,但您的比例似乎更容易受到数据结构的影响。假设我只有10k人中的3个IT工作者,那么IT内向者的比例将是10k个内向者中的3个(假设),这将是一个非常小的数字,而第二种比例(IT内向者/IT工作者)则不易受到不平等分布样本数据的影响。(即使只有3个IT工作者,它也显示为100%)。但这只是我的看法,我对您的观点很好奇:)。
数学是正确的。但是您问的是不同的问题。
IT工作者和内向者的概率是多少?与我们知道一个人在IT工作的情况下,他是内向者的概率是多少?
更正:“3%的IT工作者是内向的”= IT工作者是内向者的概率为3%。
但是我现在看到,按照文章的比例概率计算,在我的例子中,外向者的概率会是0,这将小于4%的内向者,因此结果会是内向者,这是一个正确的预测……所以这有一定道理……汗。数学和逻辑真是吓人😛
坚持下去!
非常棒的帖子——解释得太好了!
请指导一下,当有多个输入变量时,例如除了天气和汽车之外,还有“有小说要完成”和“感到疲倦”,我该如何预测类别?
在这种情况下,如何扩展该方法?
考虑使用scikit-learn内置的朴素贝叶斯,而不是自己从头开发。
https://machinelearning.org.cn/spot-check-classification-machine-learning-algorithms-python-scikit-learn/
嗨
我需要使用朴素贝叶斯来检测和防止SQL注入。
这个目的的最佳模型是什么?
并且当分类器将客户端请求识别为SQL注入攻击时,之后应该发生什么?是将请求重定向到另一个页面,还是在服务器端设置超时,还是将请求传递给代理?
谢谢^_^
我不知道,也许可以搜索一下这个主题,或者使用这个框架来构建和探索问题。
https://machinelearning.org.cn/how-to-define-your-machine-learning-problem/
嗨!
干得好,Browwnlee博士。但我仍然需要您的帮助,请您展示一下如何计算像Pima Indian Diabetes Dataset这样的训练数据的条件概率。
你好!
你是否找到了检测SQL注入的最佳模型?
在您的特定数据集上尝试一套模型,并发现哪种效果最好。
Jason,
这个博客写得非常有趣且简洁,几乎每个人都能理解。但是,我们如何利用您的方法来处理连续变量呢?
谢谢。
您可以使用高斯分布来近似变量的概率分布。
这被称为高斯朴素贝叶斯。
这种方法看起来很简单,但对于一个有许多变量值(如2000条记录)的表格,我该如何使用它?例如,假设我有一个变量电压和电池充电和放电的时间,并且我想找到剩余有用寿命,并将阈值设定为1.4V,电池电压为2.1V。鉴于这些变量有数千条数据,我该如何使用贝叶斯?
也许从清晰地定义问题开始。
https://machinelearning.org.cn/how-to-define-your-machine-learning-problem/
感谢您对朴素贝叶斯分类器的精彩概述!
不客气。
Jason博士您好
我是Python编程语言和机器学习方面的新手,我正在练习机器学习算法。在《从零开始的机器学习算法》一书中第12章“朴素贝叶斯”的练习中,我使用“Iris.csv”数据集运行得很好,但在用另一个数据集“Abseinteeism_at_work.csv”进行练习时,出现了“ZeroDivisionError: float division by zero”的错误。我在网上查找了解决错误的方法,并且已经花了几天时间,但在Stack Overflow链接上也找不到解决方案。您能否帮助我解决这个问题,以便我能继续学习这个领域?
也许数据中有一些特殊的东西导致了这个问题?
也许可以尝试逐一删除输入列,看看它对模型有何影响,以及是否能解决问题。这将帮助您缩小问题的范围。
告诉我进展如何。
先生,非常感谢。您在NB方法中是否有任何插补方法?
我认为不行。
你到底遇到了什么问题?
嗨,Jason,
我遇到了这些错误:
回溯(最近一次调用)
File “”, line 17, in
main()
File “”, line 9, in main
summaries = summarizeByClass(trainingSet)
File “”, line 43, in summarizeByClass
for classValue, instances in separated.iteritems()
AttributeError: ‘dict’ object has no attribute ‘iteritems’
抱歉,我明白了。
很高兴听到这个消息。
谢谢 Jason 先生
不客气。
Hi Jason,感谢您提供的清晰教程!
但是,有一个潜在的问题
P(h|d) = (P(d|h) * P(h)) / P(d)
如果我们计算P(d),其中d = 天气是晴天且汽车是工作,我们得到0.6 * 0.5 = 0.3
但是 (P(d|h) * P(h)) = 0.32。
因此 P(h|d) = 0.32 / 0.3,这大于1。
概率可能大于1吗?
提前感谢您的回复!
不,概率必须在0到1之间。
那么就有一个问题。当h=出行,d=(天气是晴朗且汽车是工作)
P(h|d) = 0.32 / 0.3 = 1.0666…
您对此有什么想法吗?
请注意,“|”表示“给定”,而不是“除”。
感谢您的回复。
“/”我指的是这个公式中的除号。
P(h|d) = (P(d|h) * P(h)) / P(d)
我知道我们不一定需要这个除法来进行朴素贝叶斯算法,但是,我仍然好奇地计算了P(h|d)。
我发现:
P(h|d) = (P(d|h) * P(h)) / P(d) = 0.8 * 0.8 * 0.5 / 0.3 = 0.32 / 0.3 = 1.0666…
h = 出行
d = (天气好,汽车工作)
P(d) = P(天气好,汽车工作) = P(天气好) * P(汽车工作) = 0.6 * 0.5 = 0.3
因此,P(h|d) = 1.0666… 一方面这是不可能的。但另一方面,我找不到计算概率的问题。
我明白了,谢谢。
嗨,Jason,
我非常感谢您让机器学习对非技术专业人士来说如此容易。您解释朴素贝叶斯的方式非常容易理解。我读过大量的博客和课程,但我发现当我从您的博客学习时,我学得更容易。您让机器学习对我来说非常有趣和简单。非常感谢!
谢谢!
嗨,Jason,
我们为什么要计算这些概率?
我们想得到 P(类别=出行 | 天气=晴天, 汽车=工作),因此,我们可以直接从您的表格中找到它,而无需进行任何朴素的假设。
当类别=出行时有5种情况,其中4种出现在天气=晴天且汽车=工作时。这很简单意味着:
P(类别=出行 | 天气=晴天, 汽车=工作) = 4/5
然后我们可以用类似的方式得到P(类别=在家 | 天气=晴天, 汽车=工作)。有5种类别=在家的情况,只有1种出现在天气=晴天且汽车=工作时。因此:
P(类别=在家 | 天气=晴天, 汽车=工作) = 1/5
就是这样。那么我们为什么需要您所有的计算呢?如果知道答案,提前感谢。
好问题,我想在这种情况下,我正在尝试演示基于概率运行的朴素贝叶斯方法。
Hi Jason,感谢您的有用教程!如何在不使用外部包的情况下,使用多个类别而不是二元类别(晴天、雨天、多云、下雪……)来实现它?您知道将类别转换为数字的有用方法吗?再次感谢!
上述示例直接推广到多个类别,例如从二项概率分布转换为多项概率分布。
你好 Jason,
您得出结论,这个人为构造的数据集对于任何类别都有一个类别的概率,即50%。
( ==> 5 / (5+ 5).
但是,对于第一个类别(晴天或雨天),有6个晴天和4个雨天。
我的理解是否正确,是否犯了错误?
我将第六个晴天改成了雨天(如果从列的顶部计数)。
仅供参考,您的教程布局非常简单易懂。谢谢您。
这有助于激励我继续学习机器学习课程。毕竟,它看起来并不那么难。
感谢您的反馈Muso!您说得对!