初学者常见的错误之一是在没有建立性能基准的情况下,将机器学习算法应用于问题。
一个性能基准提供了一个最低分数,高于该分数,模型就被认为在数据集中具有技能。它还为在数据集上评估的所有模型提供了相对改进的参考点。可以使用朴素分类器建立基准,例如预测测试数据集中所有样本的一个类标签。
初学者另一个常见的错误是,在类别分布不平衡的问题上,使用分类准确率作为性能指标。即使大多数类别被预测给所有案例,这也可能导致高准确率分数。相反,必须从一系列分类度量中选择一个替代的性能指标。
挑战在于性能基准取决于性能指标的选择。因此,为了选择一个合适的朴素分类器来建立性能基准,可能需要对每个性能指标有深入的了解。
在本教程中,您将发现为每个不平衡分类性能指标使用哪个朴素分类器。
完成本教程后,您将了解:
- 在评估机器学习模型用于不平衡分类问题时需要考虑的指标。
- 可用于计算模型性能基准的朴素分类模型。
- 用于每个指标的朴素分类器,包括其原理和工作示例。
启动您的项目,阅读我的新书 Python中的不平衡分类,其中包含分步教程和所有示例的Python源代码文件。
让我们开始吧。

每个不平衡分类指标的朴素分类器是什么?
照片由 土地管理局 拍摄,保留部分权利。
教程概述
本教程分为四个部分;它们是
- 不平衡分类指标
- 朴素分类模型
- 分类指标的朴素分类器
- 准确率的朴素分类器
- G-Mean 的朴素分类器
- F-Measure 的朴素分类器
- ROC AUC 的朴素分类器
- Precision-Recall AUC 的朴素分类器
- Brier Score 的朴素分类器
- 指标映射总结
不平衡分类指标
对于不平衡分类,有许多指标可供选择。
选择指标可能是项目中最重要的一步,因为选择错误的指标可能会导致优化和选择一个解决了与您实际要解决的问题不同的问题的模型。
因此,在数十甚至数百个最常用的指标中,可能有5个指标适用于不平衡分类。它们如下:
评估预测类标签的指标
- 准确率。
- G-Mean。
- F1-Measure。
- F0.5-Measure。
- F2-Measure。
评估预测概率的指标
- ROC 曲线下面积 (ROC AUC)。
- Precision Recall 曲线下面积 (PR AUC)。
- Brier Score。
有关如何计算每个指标的更多信息,请参阅教程
朴素分类模型
一个朴素分类器是一个没有逻辑的分类算法,它为分类数据集提供了一个性能基准。
为分类数据集建立性能基准很重要。它提供了一个基准,所有其他算法都可以与之进行比较。一个得分低于朴素分类模型的算法在数据集中没有技能,而一个得分高于朴素分类模型的算法在数据集中具有一定的技能。
可能存在五种不同的朴素分类方法可用于在数据集上建立性能基准。
在不平衡二分类(二元)分类问题的背景下,朴素分类方法如下:
- 均匀随机猜测:以相等的概率预测0或1。
- 先验随机猜测:根据数据集中先验概率预测0或1。
- 多数类:预测0。
- 少数类:预测1。
- 类先验:为每个类预测先验概率。
这些可以使用scikit-learn库中的DummyClassifier类来实现。
此类提供了允许使用不同朴素分类器技术的 `strategy` 参数。示例包括:
- 均匀随机猜测:将“strategy”参数设置为“uniform”。
- 先验随机猜测:将“strategy”参数设置为“stratified”。
- 多数类:将“strategy”参数设置为“most_frequent”。
- 少数类:将“strategy”参数设置为“constant”并将“constant”参数设置为1。
- 类先验:将“strategy”参数设置为“prior”。
有关朴素分类器的更多信息,请参阅教程
想要开始学习不平衡分类吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
分类指标的朴素分类器
我们已经确定,对于不平衡分类问题,有许多不同的指标可供选择。
我们还确定,使用朴素分类器为新的分类问题确定性能基准至关重要。
挑战在于,每个分类指标都需要仔细选择一个合适的朴素分类策略,以实现适当的“无技能”性能。这可以并且应该通过了解每个指标并仔细的实验来确定的。
在本节中,我们将对每个不平衡分类指标选择合适的朴素分类器进行解释,然后通过在合成二分类数据集上进行实证结果来确认选择。
合成数据集有10,000个样本,其中99%属于多数类(负案例或类别标签0),1%属于少数类(正案例或类别标签1)。
每个朴素分类器策略都使用分层10折交叉验证(重复3次)进行评估,并且性能通过这些运行的平均值和标准差进行汇总。
指标到朴素分类器的映射可以用于您的下一个不平衡分类项目,实证结果可以确认其原理并帮助建立每个映射的直观理解。
让我们开始吧。
准确率的朴素分类器
分类准确率是正确预测的总数除以所做的总预测数。
分类准确率的适当朴素分类器是在所有情况下预测多数类。这将最大化真负例并最小化假负例。
我们可以通过一个工作示例来演示这一点,该示例在二分类问题上比较了每个朴素分类器策略。我们预计预测多数类将在此数据集上产生约99%的分类准确率。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
# 比较分类准确率指标的朴素分类器 from numpy import mean from numpy import std from sklearn.datasets import make_classification from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.dummy import DummyClassifier from matplotlib import pyplot # 评估模型 def evaluate_model(X, y, model): # 定义评估过程 cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) # 评估模型 scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1) 返回 分数 # 定义要测试的模型 定义 获取_模型(): models, names = list(), list() # 均匀随机猜测 models.append(DummyClassifier(strategy='uniform')) names.append('Uniform') # 先验随机猜测 models.append(DummyClassifier(strategy='stratified')) names.append('Stratified') # 多数类:预测0 models.append(DummyClassifier(strategy='most_frequent')) names.append('Majority') # 少数类:预测1 models.append(DummyClassifier(strategy='constant', constant=1)) names.append('Minority') # 类先验 models.append(DummyClassifier(strategy='prior')) names.append('Prior') return models, names # 定义数据集 X, y = make_classification(n_samples=10000, n_features=2, n_redundant=0, n_clusters_per_class=1, weights=[0.99], flip_y=0, random_state=4) # 定义模型 models, names = get_models() results = list() # 评估每个模型 for i in range(len(models)): # 评估模型并存储结果 scores = evaluate_model(X, y, models[i]) results.append(scores) # 总结并存储 print('>%s %.3f (%.3f)' % (names[i], mean(scores), std(scores))) # 绘制结果图 pyplot.boxplot(results, labels=names, showmeans=True) pyplot.show() |
运行该示例将报告每个朴素分类器策略的分类准确率。
注意:您的结果可能因算法或评估程序的随机性、或数值精度差异而有所不同。考虑运行示例几次并比较平均结果。
在这种情况下,我们可以看到,正如预期的那样,多数类策略实现了最佳的99%分类准确率。我们还可以看到,先验策略也实现了相同的结果,因为它在所有情况下都主要预测0.01(少数类占1%),这被映射为多数类标签0。
|
1 2 3 4 5 |
>Uniform 0.501 (0.015) >Stratified 0.980 (0.003) >Majority 0.990 (0.000) >Minority 0.010 (0.000) >Prior 0.990 (0.000) |
每个朴素分类器策略的箱形图也已创建,允许直观地比较分数的分布。
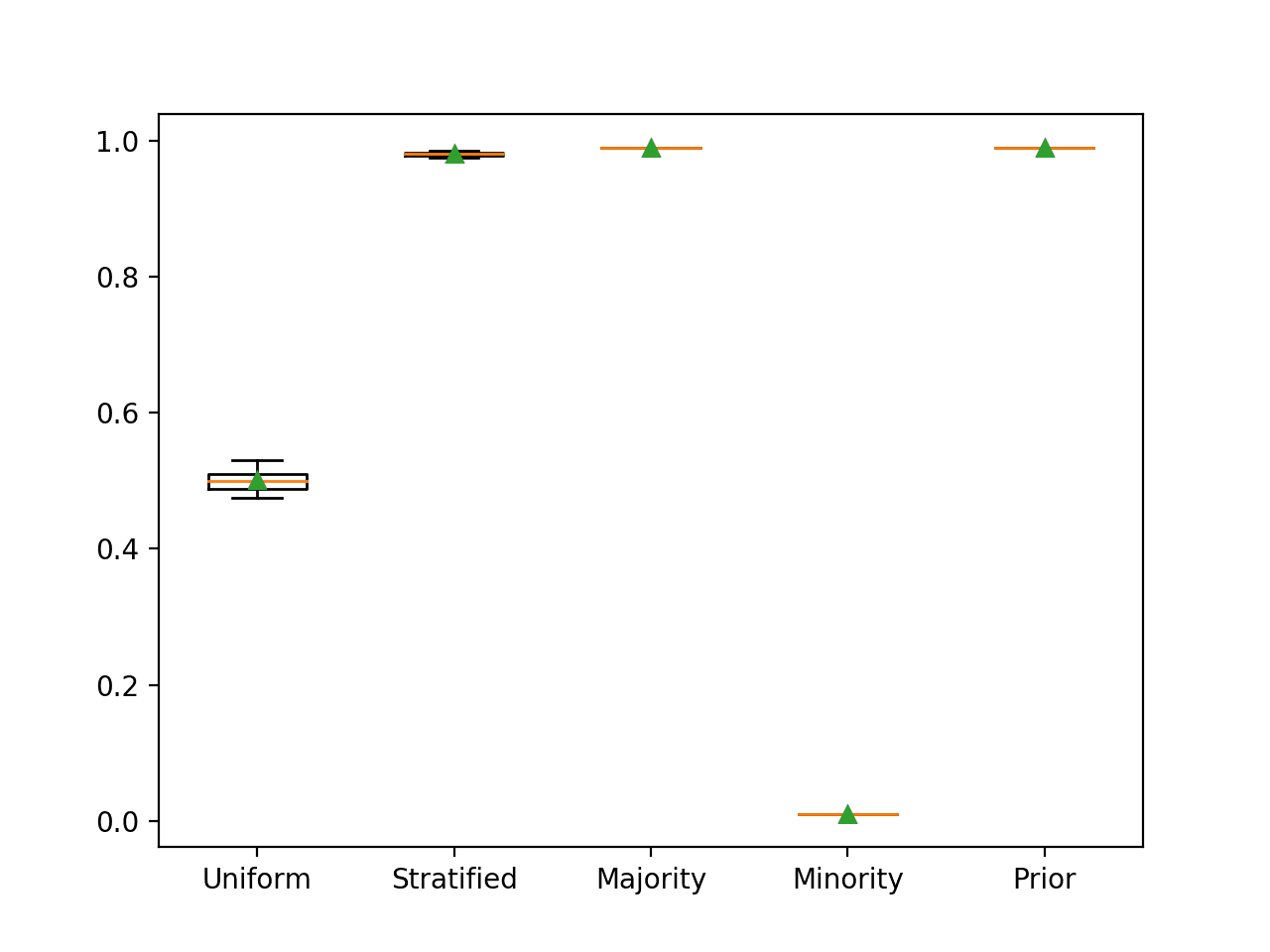
使用分类准确率评估的朴素分类器策略的箱形图
G-Mean 的朴素分类器
几何平均值,或 G-Mean,是几何平均值的敏感性和特异性分数。
敏感性总结了正面类别的预测情况,特异性总结了负面类别的预测情况。
在多数类或少数类上完美表现将以在另一类上表现最差为代价,这将导致 G-Mean 分数为零。
因此,最合适的朴素分类策略是以相等的概率预测每个类别,这将为每个类别提供正确预测的机会。
我们可以通过一个工作示例来演示这一点,该示例在二分类问题上比较了每个朴素分类器策略。我们预计预测均匀随机类标签将在此数据集上产生约0.5的 G-Mean。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 |
# 比较g-mean指标的朴素分类器 from numpy import mean from numpy import std from sklearn.datasets import make_classification from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.dummy import DummyClassifier from imblearn.metrics import geometric_mean_score from sklearn.metrics import make_scorer from matplotlib import pyplot # 评估模型 def evaluate_model(X, y, model): # 定义评估过程 cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) # 定义模型评估指标 metric = make_scorer(geometric_mean_score) # 评估模型 scores = cross_val_score(model, X, y, scoring=metric, cv=cv, n_jobs=-1) 返回 分数 # 定义要测试的模型 定义 获取_模型(): models, names = list(), list() # 均匀随机猜测 models.append(DummyClassifier(strategy='uniform')) names.append('Uniform') # 先验随机猜测 models.append(DummyClassifier(strategy='stratified')) names.append('Stratified') # 多数类:预测0 models.append(DummyClassifier(strategy='most_frequent')) names.append('Majority') # 少数类:预测1 models.append(DummyClassifier(strategy='constant', constant=1)) names.append('Minority') # 类先验 models.append(DummyClassifier(strategy='prior')) names.append('Prior') return models, names # 定义数据集 X, y = make_classification(n_samples=10000, n_features=2, n_redundant=0, n_clusters_per_class=1, weights=[0.99], flip_y=0, random_state=4) # 定义模型 models, names = get_models() results = list() # 评估每个模型 for i in range(len(models)): # 评估模型并存储结果 scores = evaluate_model(X, y, models[i]) results.append(scores) # 总结并存储 print('>%s %.3f (%.3f)' % (names[i], mean(scores), std(scores))) # 绘制结果图 pyplot.boxplot(results, labels=names, showmeans=True) pyplot.show() |
运行该示例将报告每个朴素分类器策略的 G-mean。
注意:您的结果可能因算法或评估程序的随机性、或数值精度差异而有所不同。考虑运行示例几次并比较平均结果。
在这种情况下,我们可以看到,正如预期的那样,均匀随机朴素分类器产生了0.5的 G-Mean,而所有其他策略都产生了0的 G-Mean 分数。
|
1 2 3 4 5 |
>Uniform 0.507 (0.074) >Stratified 0.021 (0.079) >Majority 0.000 (0.000) >Minority 0.000 (0.000) >Prior 0.000 (0.000) |
每个朴素分类器策略的箱形图也已创建,允许直观地比较分数的分布。
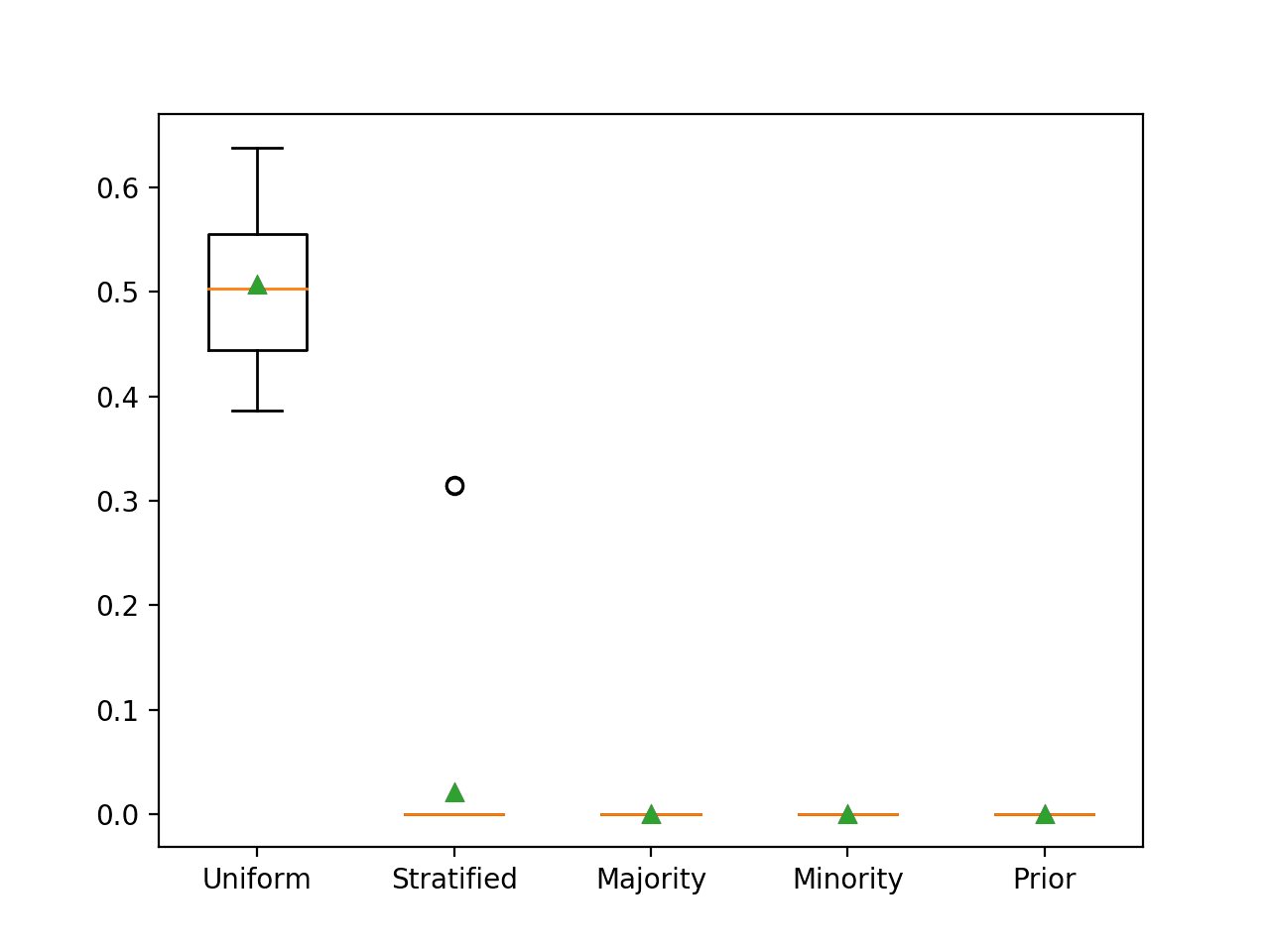
使用 G-Mean 评估的朴素分类器策略的箱形图
F-Measure 的朴素分类器
F-measure(也称为 F1-score)计算为精确率和召回率之间的调和平均值。
精确率总结了被分配到正面类别的样本中有多少属于正面类别,召回率总结了在所有可能被做出的正面预测中,有多少正面类别被成功预测。
倾向于精确率的预测(例如,预测少数类)也将导致召回率的下限。
因此,F-measure 的朴素策略是预测少数类。
我们可以通过一个工作示例来演示这一点,该示例在二分类问题上比较了每个朴素分类器策略。
对于此数据集,仅预测少数类的 F-measure 最初并不明显。召回率将是完美的,即 1.0。精确率将等同于少数类的先验概率,即 1% 或 0.01。因此,F-measure 是 1.0 和 0.01 之间的调和平均值,约为 0.02。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
# 比较f1-measure的朴素分类器 from numpy import mean from numpy import std from sklearn.datasets import make_classification from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.dummy import DummyClassifier from matplotlib import pyplot # 评估模型 def evaluate_model(X, y, model): # 定义评估过程 cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) # 评估模型 scores = cross_val_score(model, X, y, scoring='f1', cv=cv, n_jobs=-1) 返回 分数 # 定义要测试的模型 定义 获取_模型(): models, names = list(), list() # 均匀随机猜测 models.append(DummyClassifier(strategy='uniform')) names.append('Uniform') # 先验随机猜测 models.append(DummyClassifier(strategy='stratified')) names.append('Stratified') # 多数类:预测0 models.append(DummyClassifier(strategy='most_frequent')) names.append('Majority') # 少数类:预测1 models.append(DummyClassifier(strategy='constant', constant=1)) names.append('Minority') # 类先验 models.append(DummyClassifier(strategy='prior')) names.append('Prior') return models, names # 定义数据集 X, y = make_classification(n_samples=10000, n_features=2, n_redundant=0, n_clusters_per_class=1, weights=[0.99], flip_y=0, random_state=4) # 定义模型 models, names = get_models() results = list() # 评估每个模型 for i in range(len(models)): # 评估模型并存储结果 scores = evaluate_model(X, y, models[i]) results.append(scores) # 总结并存储 print('>%s %.3f (%.3f)' % (names[i], mean(scores), std(scores))) # 绘制结果图 pyplot.boxplot(results, labels=names, showmeans=True) pyplot.show() |
运行该示例将报告每个朴素分类器策略的 ROC AUC。
注意:您的结果可能因算法或评估程序的随机性、或数值精度差异而有所不同。考虑运行示例几次并比较平均结果。
当评估仅预测少数类的朴素分类器时,您可能会收到警告,因为没有预测到正面案例。您将看到如下警告:
|
1 |
UndefinedMetricWarning: F-score is ill-defined and being set to 0.0 due to no predicted samples. |
在这种情况下,我们可以看到,预测少数类导致了预期的 F-measure 约为 0.02。我们还可以看到,使用均匀和分层策略时,我们近似了该分数。
|
1 2 3 4 5 |
>Uniform 0.020 (0.007) >Stratified 0.020 (0.040) >Majority 0.000 (0.000) >Minority 0.020 (0.000) >Prior 0.000 (0.000) |
每个朴素分类器策略的箱形图也已创建,允许直观地比较分数的分布。
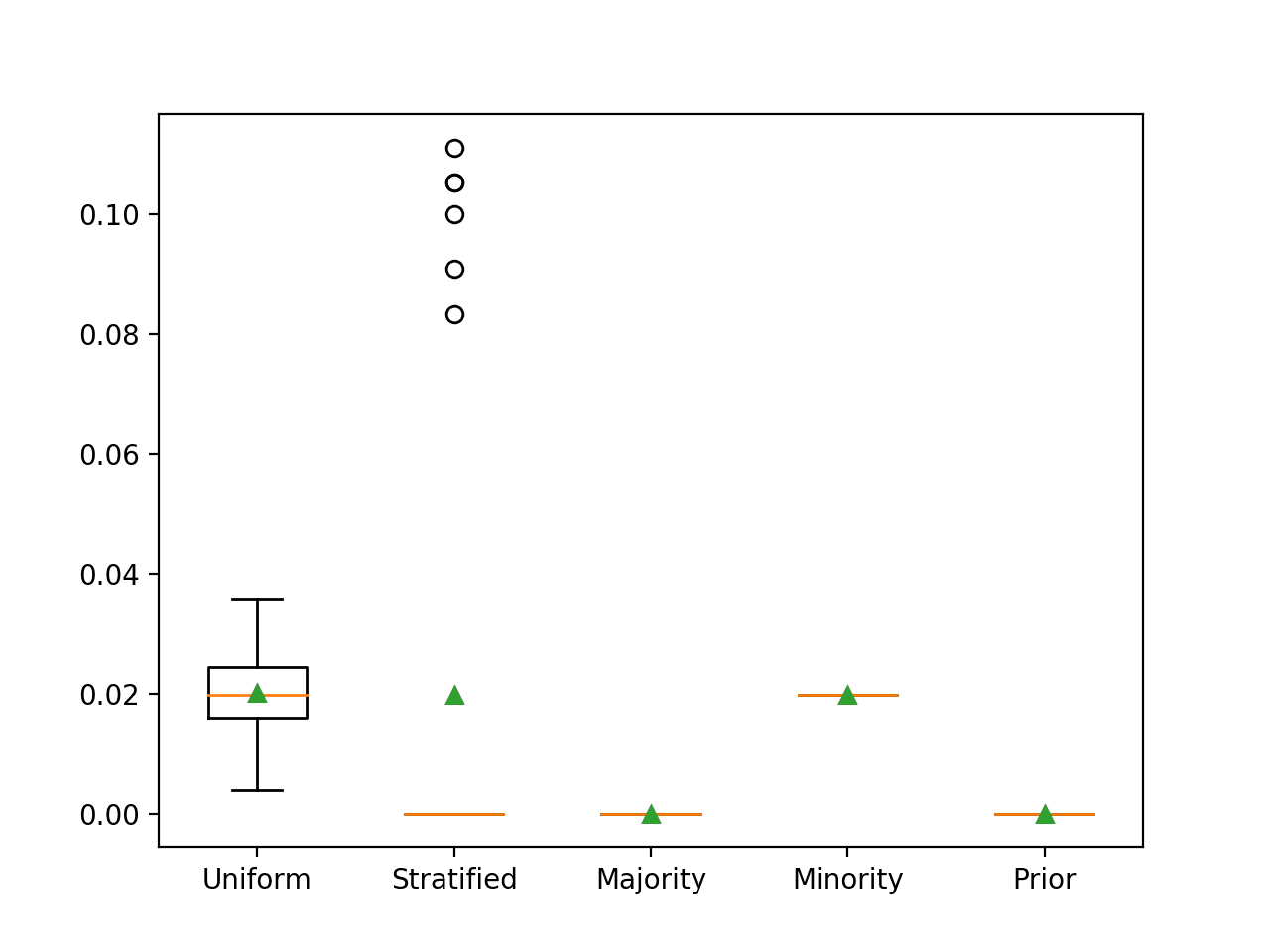
使用 F-Measure 评估的朴素分类器策略的箱形图
使用少数类进行预测的相同朴素分类器策略也适用于 F0.5 和 F2 度量。
ROC AUC 的朴素分类器
ROC 曲线是针对一系列不同概率阈值绘制的假阳性率与真阳性率的关系图。
ROC 曲线下面积是 ROC 曲线的积分或面积的近似值,总结了算法在整个概率阈值范围内的性能。
无技能模型具有 0.5 的 ROC AUC,可以通过随机但按其基础速率(例如,无区分能力)比例预测类标签来实现。这将是分层方法。
预测一个恒定值,如多数类或少数类,将导致 ROC 曲线无效(例如,一个点),进而导致 ROC AUC 分数无效。应忽略预测恒定值的模型的得分。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
# 比较roc auc的朴素分类器 from numpy import mean from numpy import std from sklearn.datasets import make_classification from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.dummy import DummyClassifier from matplotlib import pyplot # 评估模型 def evaluate_model(X, y, model): # 定义评估过程 cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) # 评估模型 scores = cross_val_score(model, X, y, scoring='roc_auc', cv=cv, n_jobs=-1) 返回 分数 # 定义要测试的模型 定义 获取_模型(): models, names = list(), list() # 均匀随机猜测 models.append(DummyClassifier(strategy='uniform')) names.append('Uniform') # 先验随机猜测 models.append(DummyClassifier(strategy='stratified')) names.append('Stratified') # 多数类:预测0 models.append(DummyClassifier(strategy='most_frequent')) names.append('Majority') # 少数类:预测1 models.append(DummyClassifier(strategy='constant', constant=1)) names.append('Minority') # 类先验 models.append(DummyClassifier(strategy='prior')) names.append('Prior') return models, names # 定义数据集 X, y = make_classification(n_samples=10000, n_features=2, n_redundant=0, n_clusters_per_class=1, weights=[0.99], flip_y=0, random_state=4) # 定义模型 models, names = get_models() results = list() # 评估每个模型 for i in range(len(models)): # 评估模型并存储结果 scores = evaluate_model(X, y, models[i]) results.append(scores) # 总结并存储 print('>%s %.3f (%.3f)' % (names[i], mean(scores), std(scores))) # 绘制结果图 pyplot.boxplot(results, labels=names, showmeans=True) pyplot.show() |
运行该示例将报告每个朴素分类器策略的 ROC AUC。
注意:您的结果可能因算法或评估程序的随机性、或数值精度差异而有所不同。考虑运行示例几次并比较平均结果。
在这种情况下,我们可以看到,正如预期的那样,预测一个分层的随机标签会导致最差的 ROC AUC,即 0.5。
|
1 2 3 4 5 |
>Uniform 0.500 (0.000) >Stratified 0.506 (0.020) >Majority 0.500 (0.000) >Minority 0.500 (0.000) >Prior 0.500 (0.000) |
每个朴素分类器策略的箱形图也已创建,允许直观地比较分数的分布。
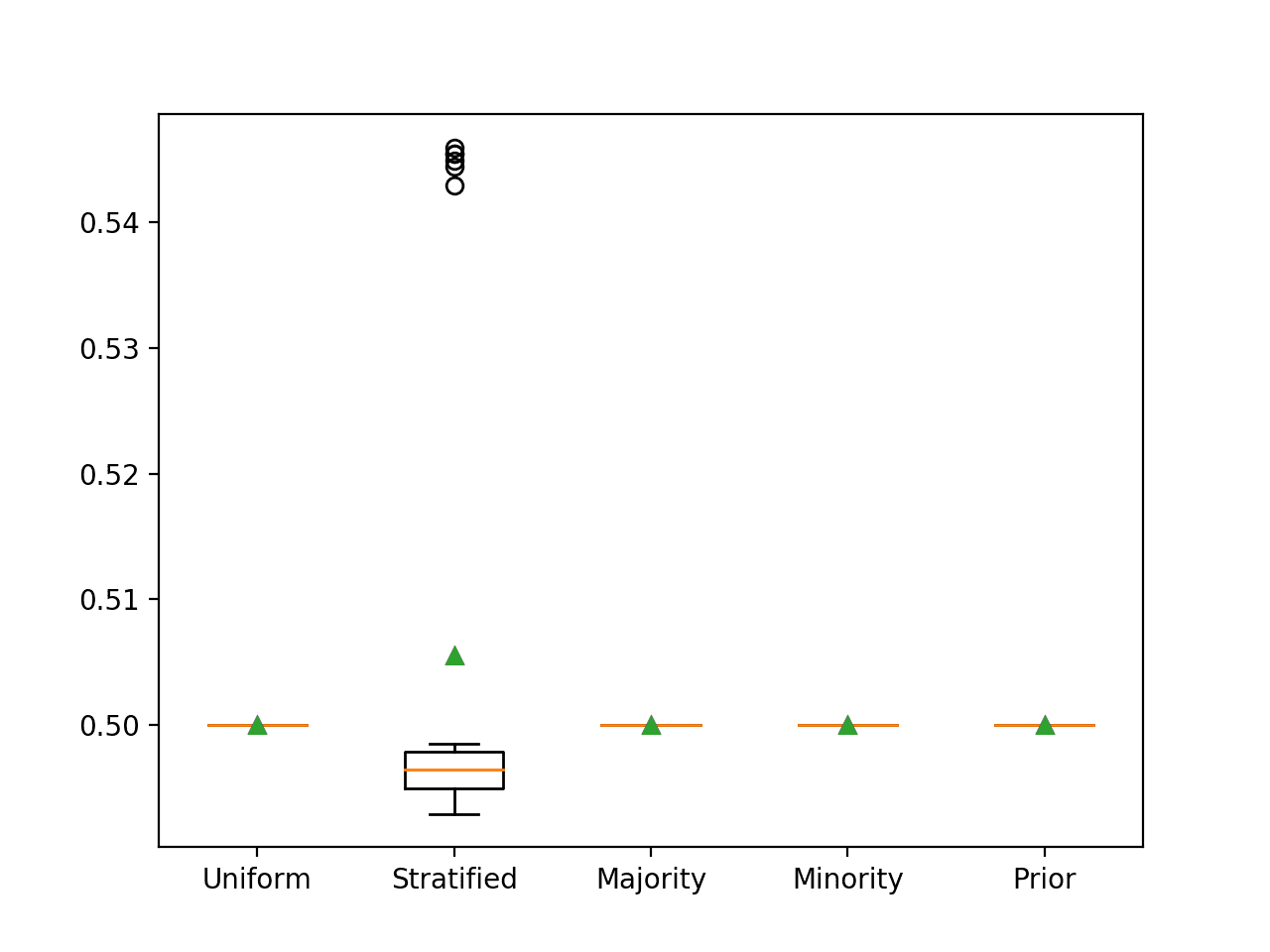
使用 ROC AUC 评估的朴素分类器策略的箱形图
Precision-Recall AUC 的朴素分类器
Precision-Recall 曲线(或 PR 曲线)是针对一系列不同概率阈值绘制的召回率与精确率的关系图。
Precision-Recall 曲线下面积是 Precision-Recall 曲线的积分或面积的近似值,总结了算法在整个概率阈值范围内的性能。
无技能模型具有接近正类基础速率的 PR AUC,例如 0.01。这可以通过随机但按其基础速率(例如,无区分能力)比例预测类标签来实现。这将是分层方法。
预测一个恒定值,如多数类或少数类,将导致 PR 曲线无效(例如,一个点),进而导致 PR AUC 分数无效。应忽略预测恒定值的模型的得分。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 |
# 比较precision-recall auc指标的朴素分类器 from numpy import mean from numpy import std from sklearn.datasets import make_classification from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.dummy import DummyClassifier from sklearn.metrics import precision_recall_curve from sklearn.metrics import auc from sklearn.metrics import make_scorer from matplotlib import pyplot # 计算precision-recall area under curve def pr_auc(y_true, probas_pred): # 计算precision-recall curve p, r, _ = precision_recall_curve(y_true, probas_pred) # calculate area under curve return auc(r, p) # 评估模型 def evaluate_model(X, y, model): # 定义评估过程 cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) # 定义模型评估指标 metric = make_scorer(pr_auc, needs_proba=True) # 评估模型 scores = cross_val_score(model, X, y, scoring=metric, cv=cv, n_jobs=-1) 返回 分数 # 定义要测试的模型 定义 获取_模型(): models, names = list(), list() # 均匀随机猜测 models.append(DummyClassifier(strategy='uniform')) names.append('Uniform') # 先验随机猜测 models.append(DummyClassifier(strategy='stratified')) names.append('Stratified') # 多数类:预测0 models.append(DummyClassifier(strategy='most_frequent')) names.append('Majority') # 少数类:预测1 models.append(DummyClassifier(strategy='constant', constant=1)) names.append('Minority') # 类先验 models.append(DummyClassifier(strategy='prior')) names.append('Prior') return models, names # 定义数据集 X, y = make_classification(n_samples=10000, n_features=2, n_redundant=0, n_clusters_per_class=1, weights=[0.99], flip_y=0, random_state=4) # 定义模型 models, names = get_models() results = list() # 评估每个模型 for i in range(len(models)): # 评估模型并存储结果 scores = evaluate_model(X, y, models[i]) results.append(scores) # 总结并存储 print('>%s %.3f (%.3f)' % (names[i], mean(scores), std(scores))) # 绘制结果图 pyplot.boxplot(results, labels=names, showmeans=True) pyplot.show() |
运行该示例将报告每个朴素分类器策略的 PR AUC 分数。
注意:您的结果可能因算法或评估程序的随机性、或数值精度差异而有所不同。考虑运行示例几次并比较平均结果。
在这种情况下,我们可以看到,正如预期的那样,预测一个分层的随机类标签会导致最差的 PR AUC,接近 0.01。
|
1 2 3 4 5 |
>Uniform 0.505 (0.000) >Stratified 0.015 (0.037) >Majority 0.505 (0.000) >Minority 0.505 (0.000) >Prior 0.505 (0.000) |
每个朴素分类器策略的箱形图也已创建,允许直观地比较分数的分布。
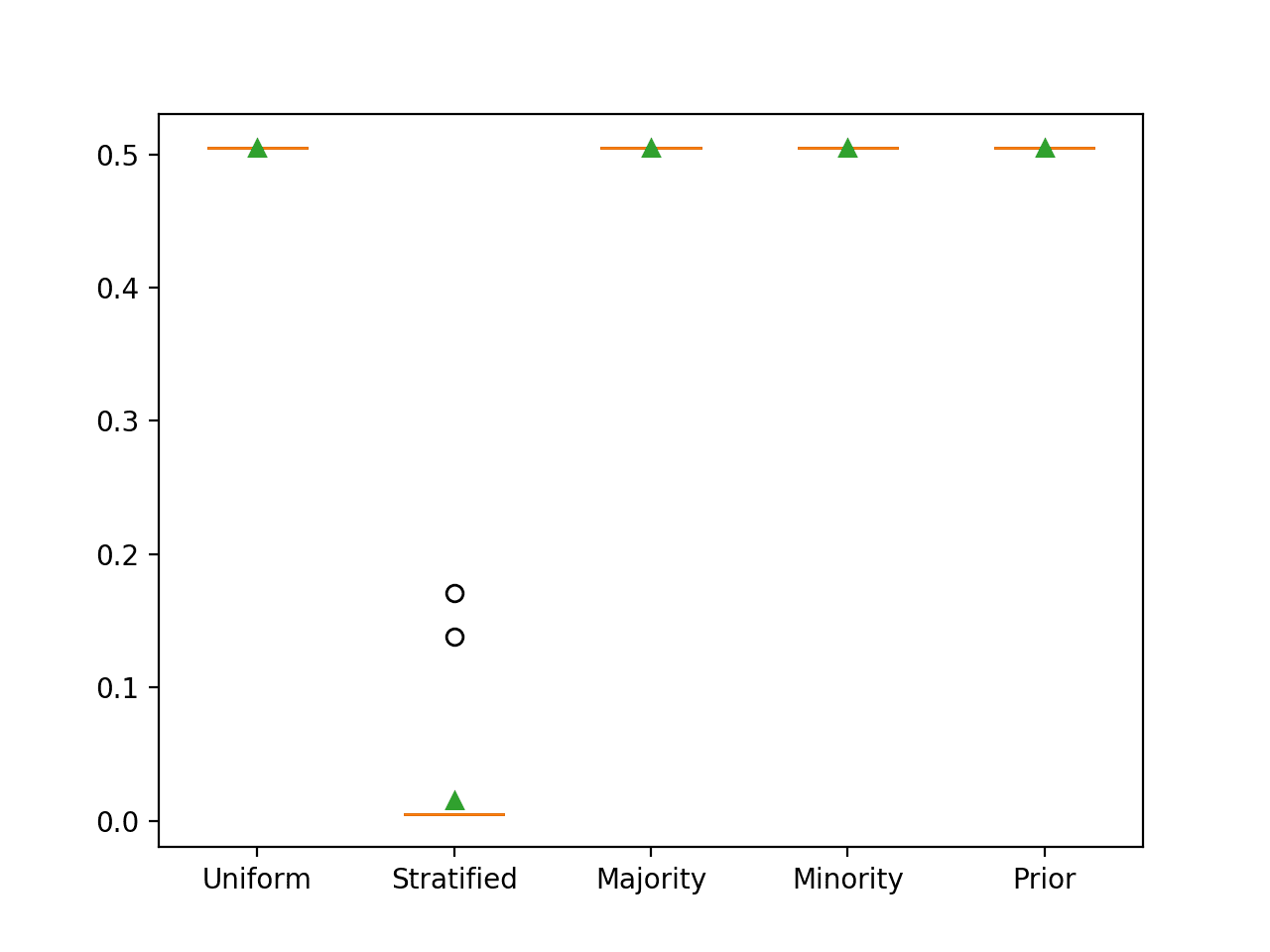
使用 Precision-Recall AUC 评估的朴素分类器策略的箱形图
Brier Score 的朴素分类器
Brier score 计算预期概率与预测概率之间的均方误差。
Brier score 的适当朴素分类器是在测试集中预测每个样本的类先验。对于涉及预测二项分布的二分类问题,这将是类0的先验和类1的先验。
我们可以通过一个工作示例来演示这一点,该示例在二分类问题上比较了每个朴素分类器策略。
模型将在所有情况下预测概率 [0.99, 0.01]。我们预计这将导致均方误差接近少数类的先验,即此数据集上的 0.01。这是因为大多数样本的二项概率为0.0,只有1%的样本为1.0,这导致1%的案例出现最大误差,或Brier score为0.01。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
# 比较brier score指标的朴素分类器 from numpy import mean from numpy import std from sklearn.datasets import make_classification from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.dummy import DummyClassifier from matplotlib import pyplot # 评估模型 def evaluate_model(X, y, model): # 定义评估过程 cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) # 评估模型 scores = cross_val_score(model, X, y, scoring='brier_score_loss', cv=cv, n_jobs=-1) 返回 分数 # 定义要测试的模型 定义 获取_模型(): models, names = list(), list() # 均匀随机猜测 models.append(DummyClassifier(strategy='uniform')) names.append('Uniform') # 先验随机猜测 models.append(DummyClassifier(strategy='stratified')) names.append('Stratified') # 多数类:预测0 models.append(DummyClassifier(strategy='most_frequent')) names.append('Majority') # 少数类:预测1 models.append(DummyClassifier(strategy='constant', constant=1)) names.append('Minority') # 类先验 models.append(DummyClassifier(strategy='prior')) names.append('Prior') return models, names # 定义数据集 X, y = make_classification(n_samples=10000, n_features=2, n_redundant=0, n_clusters_per_class=1, weights=[0.99], flip_y=0, random_state=4) # 定义模型 models, names = get_models() results = list() # 评估每个模型 for i in range(len(models)): # 评估模型并存储结果 scores = evaluate_model(X, y, models[i]) results.append(scores) # 总结并存储 print('>%s %.3f (%.3f)' % (names[i], mean(scores), std(scores))) # 绘制结果图 pyplot.boxplot(results, labels=names, showmeans=True) pyplot.show() |
运行该示例将报告每个朴素分类器策略的 Brier score。
注意:您的结果可能因算法或评估程序的随机性、或数值精度差异而有所不同。考虑运行示例几次并比较平均结果。
Brier score 被最小化,0.0 表示可能获得的最低分数。
因此,scikit-learn 通过使其变为负数来反转分数,因此每个朴素分类器都具有负的平均 Brier 分数。因此,可以忽略符号。
正如预期的那样,我们可以看到预测先验概率会获得最佳分数。我们还可以看到,预测多数类也会获得相同的最佳 Brier 分数。
|
1 2 3 4 5 |
>Uniform -0.250 (0.000) >Stratified -0.020 (0.003) >Majority -0.010 (0.000) >Minority -0.990 (0.000) >Prior -0.010 (0.000) |
每个朴素分类器策略的箱形图也已创建,允许直观地比较分数的分布。
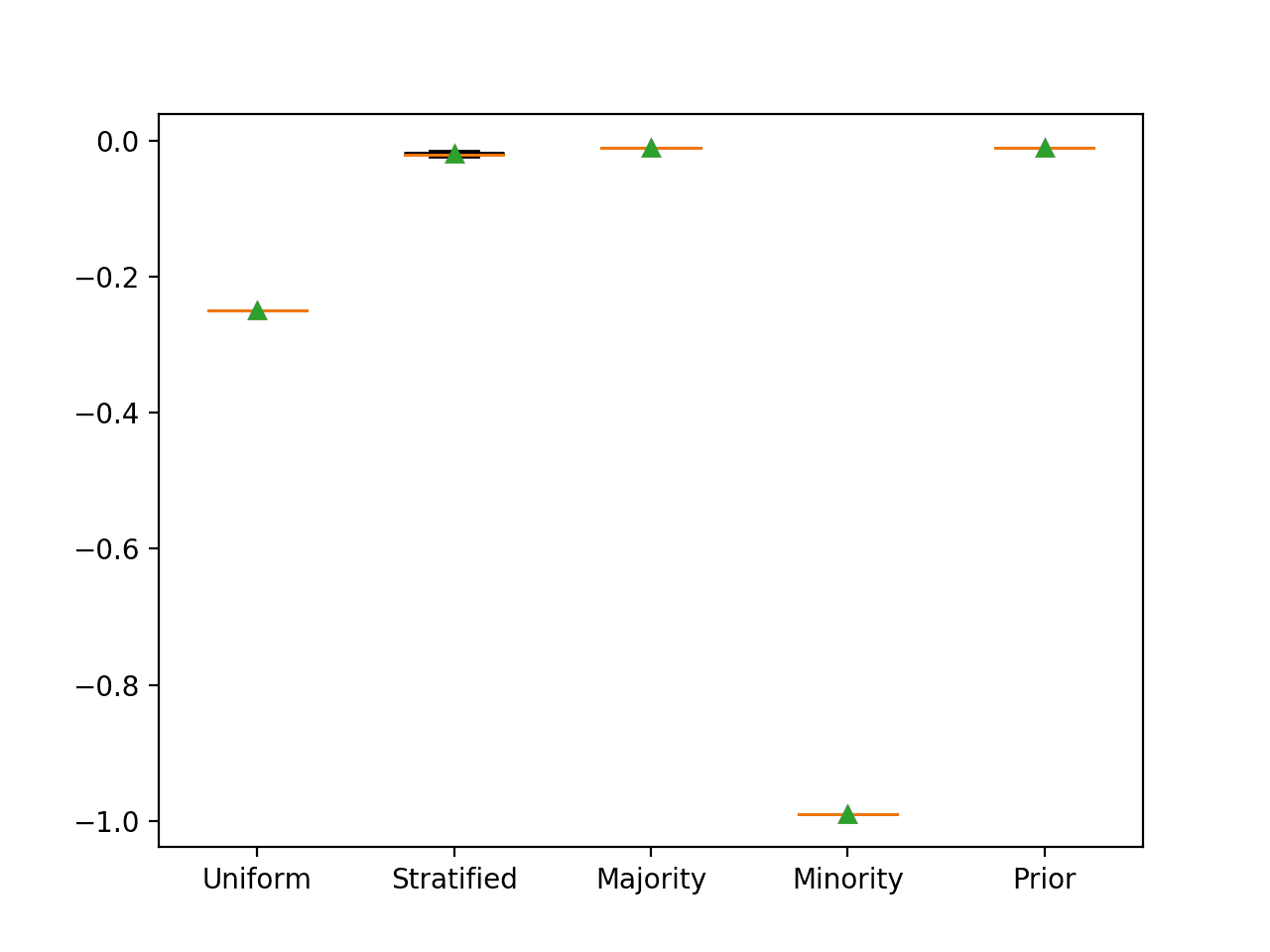
朴素分类器策略的箱线图,使用 Brier 分数进行评估
指标映射总结
我们可以总结不平衡分类指标到朴素分类方法的映射。
这提供了一个查找表,您可以在下一个不平衡分类项目中进行查阅。
- 准确率:预测多数类(类别 0)。
- G-平均数:预测均匀随机类别。
- F1 分数:预测少数类(类别 1)。
- F0.5 分数:预测少数类(类别 1)。
- F2 分数:预测少数类(类别 1)。
- ROC AUC:预测分层随机类别。
- PR ROC:预测分层随机类别。
- Brier 分数:预测多数类先验。
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
教程
API
总结
在本教程中,您发现了为每个不平衡分类性能指标应使用的朴素分类器。
具体来说,你学到了:
- 在评估机器学习模型用于不平衡分类问题时需要考虑的指标。
- 可用于计算模型性能基准的朴素分类模型。
- 用于每个指标的朴素分类器,包括其原理和工作示例。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。






对于一个多类别不平衡问题,我希望使用准确率、精确率、召回率和 F 分数作为我的评估指标。
使用预测少数类的虚拟分类器来获得所有上述指标的基线性能是否正确?
或者是否有其他好的方法来解决这个问题。
谢谢
San
我强烈建议选择一个指标进行优化。
我能知道原因吗?
谢谢
San
是的,同时优化多个指标会导致优先级的混淆,并在所有指标上产生糟糕的结果。
谢谢,清楚多了。
谢谢。
您好!我认为精确率和召回率在这段中是颠倒的
“精确率总结了被分配到正类别的样本中属于正类别的比例,而召回率总结了在所有可能做出的正预测中,正类别被预测得有多好。”
精确率或阳性预测值,意味着真阳性预测的总数除以总预测数。召回率或真阳性率是真阳性总数除以所有阳性样本的总数。
这可能有帮助
https://machinelearning.org.cn/fbeta-measure-for-machine-learning/
这些例子是二分类。我有一个多类别问题。当类别超过 2 个时,会有什么变化?
变化不大,只需向指标指定哪些类别是正例,哪些是负例。
例如,这里的文档将有所帮助
https://scikit-learn.cn/stable/modules/generated/sklearn.metrics.precision_score.html
请在此处查看多类别示例
https://machinelearning.org.cn/precision-recall-and-f-measure-for-imbalanced-classification/
嗨,Jason,
我对这个教程有几个问题
1.如果数据集与本教程中使用的数据集不同,那么朴素分类器的分数指标值会改变吗?例如,在本教程数据集上使用均匀策略的 PR AUC 度量值为 0.505。对于其他数据集是否相同?
2.在映射摘要中,它提到了 ROC AUC:预测分层随机类别。
PR ROC:预测分层随机类别。Brier 分数:预测多数类先验。这三个指标都是用于不平衡数据集的概率预测评估。我仍然不明白“预测分层随机类别”以及“预测多数类先验”是什么意思?您能指导一下吗?特别是对于 Brier 分数,为什么它预测多数类先验,而它用于不平衡数据集?
感谢您的回复
分数会根据测试集的构成而变化。
是的,也许这个教程能更好地解释朴素分类器。
https://machinelearning.org.cn/how-to-develop-and-evaluate-naive-classifier-strategies-using-probability/
感谢分享您的知识,Brownlee 博士!如果我理解您帖子的意思,那么其思想是选择一种朴素策略,该策略在您感兴趣的指标上比其他策略表现更好。这就是我们可以用来与模型进行比较的“无技能”基线。在您的摘要中,似乎选择了最佳场景。除了 PR AUC,您说预测一个分层随机类别,但这种策略的表现远不如其他所有策略(0.015 对比 0.505)。这是笔误还是有推荐表现较差策略的原因?
对于该指标来说,这在技术上是正确的方法——分数接近类别比例。其他的指标是根据记忆最大化精确率或召回率。
在您的回复和再次查看 PR AUC 和 F 分数部分的信息后,我明白了。谢谢!
不客气。
读完这个教程后,我仍然感到困惑。
1. 为什么要看这 5 个选项的图表?
目标是找到 5 个中提供最大指标值的,并将其作为基线吗?(因为更高的性能更好?)
这个想法与我在准确率图表中看到的一致(多数类在那里最高),G-平均数(均匀随机在那里最高),F 分数不一致(均匀随机的平均数与少数类相同,但它有超过少数类的异常值,为什么选择少数类?),ROC AUC 一致(选择了分层随机类),但在 PR AUC 中完全相反(我期望总是选择最高的,但选择的分层随机类是最低的策略)。那么我们如何看待这些现象?
2. ROC AUC 需要非阈值的预测概率。DummyClassifier 如何提供这些?它不是只根据某些规则输出 1/0,这会不会破坏创建 ROC 所需的排序?
3. 本文讨论了一个 1:99 比例的正例/负例的数据集。当类别比例改变时,整个分析会有什么变化?
图表是为了确认数值发现——这样你就可以建立直觉。也许这对你没有帮助。
默认/朴素分类器不根据数据集而改变,只根据所选指标而改变。
具体的指标值会根据数据准备、模型、模型配置等选择而变化。
>“预测一个恒定的值,比如多数类或少数类,将导致无效的 ROC 曲线(例如,一个点)”
我有一些担忧。在为 roc_auc 和 pr_auc 指标建议的“分层”策略下,虚拟分类器将输出离散的 {0,1} 类值,而不是连续概率。而“先验”会导致所有样本的单一、恒定概率,从而导致无效的单点曲线。