评估用于预测家庭用电量的朴素模型

作者 Jason Brownlee 于 2020年8月28日分类于时间序列深度学习 23

随着智能电表和太阳能电池板等发电技术的广泛应用，大量的用电数据可供使用。

这些数据代表了一个与电力相关的多元时间序列，进而可以用于建模甚至预测未来的用电量。

在本教程中，您将了解如何为“家庭用电量”数据集开发测试框架，并评估三种朴素预测策略，为更复杂的算法提供基准。

完成本教程后，您将了解：

如何加载、准备和降采样家庭用电量数据集，为开发模型做好准备。
如何开发指标、数据集拆分以及前向验证元素，为评估预测模型构建强大的测试框架。
如何开发、评估和比较一系列朴素的持续性预测方法的性能。

立即开始您的项目，阅读我的新书《时间序列预测深度学习》，其中包含分步教程以及所有示例的Python源代码文件。

让我们开始吧。

How to Develop and Evaluate Naive Forecast Methods for Forecasting Household Electricity Consumption

如何开发和评估家庭用电量预测的朴素预测方法
照片由 Philippe Put 拍摄，部分权利保留。

教程概述

本教程分为四个部分；它们是

问题描述
加载并准备数据集
模型评估
朴素预测模型

问题描述

“家庭用电量”数据集是一个多元时间序列数据集，描述了单个家庭四年的用电量。

数据收集于 2006 年 12 月至 2010 年 11 月期间，每分钟收集一次家庭用电量的观测值。

它是一个多元序列，包含七个变量（除了日期和时间）；它们是

global_active_power：家庭消耗的总有功功率（千瓦）。
global_reactive_power：家庭消耗的总无功功率（千瓦）。
voltage：平均电压（伏特）。
global_intensity：平均电流强度（安培）。
sub_metering_1：厨房的有功电能（瓦时有功电能）。
sub_metering_2：洗衣房的有功电能（瓦时有功电能）。
sub_metering_3：气候控制系统的有功电能（瓦时有功电能）。

有功电能和无功电能指的是交流电的技术细节。

第四个子计量变量可以通过将三个定义的子计量变量的总和从总有功电能中减去来创建，如下所示

sub_metering_remainder = (global_active_power * 1000 / 60) - (sub_metering_1 + sub_metering_2 + sub_metering_3)

1	sub_metering_remainder = (global_active_power * 1000 / 60) - (sub_metering_1 + sub_metering_2 + sub_metering_3)

加载并准备数据集

该数据集可以从 UCI 机器学习仓库下载，为一个 20 兆字节的 .zip 文件

household_power_consumption.zip

下载数据集并将其解压缩到当前工作目录。现在您将拥有文件“household_power_consumption.txt”，其大小约为 127 兆字节，并包含所有观测值。

我们可以使用 read_csv() 函数加载数据，并将前两列合并为一个日期时间列，我们可以将其用作索引。

# load all data
dataset = read_csv('household_power_consumption.txt', sep=';', header=0, low_memory=False, infer_datetime_format=True, parse_dates={'datetime':[0,1]}, index_col=['datetime'])

1 2	# 加载所有数据 dataset = read_csv('household_power_consumption.txt', sep=';', header=0, low_memory=False, infer_datetime_format=True, parse_dates={'datetime':[0,1]}, index_col=['datetime'])

接下来，我们可以将用“?”字符表示的所有缺失值标记为 NaN 值，这是一个浮点数。

这将允许我们以一个浮点值数组而不是混合类型（效率较低）来处理数据。

# mark all missing values
dataset.replace('?', nan, inplace=True)
# make dataset numeric
dataset = dataset.astype('float32')

# 标记所有缺失值

dataset.replace('?', nan, inplace=True)

# 使数据集数值化

dataset = dataset.astype('float32')

现在我们需要填补已标记的缺失值。

一个非常简单的方法是复制前一天同一时间的观测值。我们可以在一个名为 fill_missing() 的函数中实现这一点，该函数将接收数据的 NumPy 数组并复制 24 小时前的值。

# fill missing values with a value at the same time one day ago
def fill_missing(values):
	one_day = 60 * 24
	for row in range(values.shape[0]):
		for col in range(values.shape[1]):
			if isnan(values[row, col]):
				values[row, col] = values[row - one_day, col]

# 用一天前同一时间的值填充缺失值

def fill_missing(values):

one_day = 60 * 24

for row in range(values.shape[0]):

for col in range(values.shape[1]):

if isnan(values[row, col]):

values[row, col] = values[row - one_day, col]

我们可以直接将此函数应用于 DataFrame 中的数据。

# fill missing
fill_missing(dataset.values)

1 2	# 填充缺失值 fill_missing(dataset.values)

现在我们可以创建一个新列，其中包含子计量的剩余部分，使用上一节中的计算。

# add a column for for the remainder of sub metering
values = dataset.values
dataset['sub_metering_4'] = (values[:,0] * 1000 / 60) - (values[:,4] + values[:,5] + values[:,6])

# 添加一个用于子计量剩余部分的新列

values = dataset.values

dataset['sub_metering_4'] = (values[:,0] * 1000 / 60) - (values[:,4] + values[:,5] + values[:,6])

现在我们可以将清理后的数据集保存到一个新文件中；在这种情况下，我们只需将文件扩展名更改为 .csv 并将数据集保存为“household_power_consumption.csv”。

# save updated dataset
dataset.to_csv('household_power_consumption.csv')

1 2	# 保存更新后的数据集 dataset.to_csv('household_power_consumption.csv')

将所有这些串联起来，加载、清理和保存数据集的完整示例列在下面。

# load and clean-up data
from numpy import nan
from numpy import isnan
from pandas import read_csv
from pandas import to_numeric

# fill missing values with a value at the same time one day ago
def fill_missing(values):
	one_day = 60 * 24
	for row in range(values.shape[0]):
		for col in range(values.shape[1]):
			if isnan(values[row, col]):
				values[row, col] = values[row - one_day, col]

# load all data
dataset = read_csv('household_power_consumption.txt', sep=';', header=0, low_memory=False, infer_datetime_format=True, parse_dates={'datetime':[0,1]}, index_col=['datetime'])
# mark all missing values
dataset.replace('?', nan, inplace=True)
# make dataset numeric
dataset = dataset.astype('float32')
# fill missing
fill_missing(dataset.values)
# add a column for for the remainder of sub metering
values = dataset.values
dataset['sub_metering_4'] = (values[:,0] * 1000 / 60) - (values[:,4] + values[:,5] + values[:,6])
# save updated dataset
dataset.to_csv('household_power_consumption.csv')

# 加载和清理数据

from numpy import nan

from numpy import isnan

from pandas import read_csv

from pandas import to_numeric

# 用一天前同一时间的值填充缺失值

def fill_missing(values):

one_day = 60 * 24

for row in range(values.shape[0]):

for col in range(values.shape[1]):

if isnan(values[row, col]):

values[row, col] = values[row - one_day, col]

# 加载所有数据

dataset = read_csv('household_power_consumption.txt', sep=';', header=0, low_memory=False, infer_datetime_format=True, parse_dates={'datetime':[0,1]}, index_col=['datetime'])

# 标记所有缺失值

dataset.replace('?', nan, inplace=True)

# 使数据集数值化

dataset = dataset.astype('float32')

# 填充缺失值

fill_missing(dataset.values)

# 添加一个用于子计量剩余部分的新列

values = dataset.values

dataset['sub_metering_4'] = (values[:,0] * 1000 / 60) - (values[:,4] + values[:,5] + values[:,6])

# 保存更新后的数据集

dataset.to_csv('household_power_consumption.csv')

运行示例会创建一个新的文件“household_power_consumption.csv”，我们可以将其作为建模项目的起点。

时间序列深度学习需要帮助吗？

立即参加我为期7天的免费电子邮件速成课程（附示例代码）。

点击注册，同时获得该课程的免费PDF电子书版本。

模型评估

在本节中，我们将考虑如何为家庭用电数据集开发和评估预测模型。

本节分为四个部分；它们是

问题构建
评估指标
训练集和测试集
逐时验证

问题构建

有许多方法可以利用和探索家庭用电量数据集。

在本教程中，我们将使用数据来探索一个非常具体的问题；那就是

鉴于最近的用电量，未来一周的预期用电量是多少？

这要求预测模型预测未来七天每天的总有功功率。

严格来说，这种问题框架被称为多步时间序列预测问题，因为它包含多个预测步。使用多个输入变量的模型可能被称为多元多步时间序列预测模型。

这种类型的模型可能有助于家庭规划开支。它也可能有助于供应方规划特定家庭的电力需求。

这种数据集的框架还表明，将每分钟的用电量观测值下采样到每日总计可能很有用。这不是必需的，但考虑到我们关注的是每天的总功率，这样做是合理的。

我们可以轻松地通过 Pandas DataFrame 上的 resample() 函数来实现这一点。将参数 ‘D‘ 传递给此函数，可以按天对由日期时间索引的数据进行分组（查看所有偏移别名）。然后，我们可以计算每天所有观测值的总和，并为每个变量创建一个新的每日用电量数据数据集。

完整的示例如下所示。

# resample minute data to total for each day
from pandas import read_csv
# load the new file
dataset = read_csv('household_power_consumption.csv', header=0, infer_datetime_format=True, parse_dates=['datetime'], index_col=['datetime'])
# resample data to daily
daily_groups = dataset.resample('D')
daily_data = daily_groups.sum()
# summarize
print(daily_data.shape)
print(daily_data.head())
# save
daily_data.to_csv('household_power_consumption_days.csv')

# 将分钟数据重新采样为每天的总量

from pandas import read_csv

# 加载新文件

dataset = read_csv('household_power_consumption.csv', header=0, infer_datetime_format=True, parse_dates=['datetime'], index_col=['datetime'])

# 将数据重新采样为每日数据

daily_groups = dataset.resample('D')

daily_data = daily_groups.sum()

# 总结

print(daily_data.shape)

print(daily_data.head())

# 保存

daily_data.to_csv('household_power_consumption_days.csv')

运行示例将创建一个新的每日总用电量数据集，并将结果保存到一个名为“household_power_consumption_days.csv”的单独文件中。

我们可以将其用作拟合和评估所选问题框架的预测模型的数据集。

评估指标

预测将由七个值组成，未来一周的每一天一个值。

在多步预测问题中，通常会单独评估每个预测时间步长。这有几个原因

评论特定提前期（例如，+1 天与 +3 天）的技能。
根据模型在不同提前期（例如，+1 天擅长的模型与 +5 天擅长的模型）的技能来对比模型。

总功率的单位是千瓦，拥有一个相同单位的误差度量将很有用。均方根误差 (RMSE) 和平均绝对误差 (MAE) 都符合这个要求，尽管 RMSE 更常用，并将在本教程中采用。与 MAE 不同，RMSE 对预测误差的惩罚更大。

此问题的性能指标将是第 1 天到第 7 天每个提前期的 RMSE。

作为一种捷径，为了帮助模型选择，使用单个分数来总结模型的性能可能很有用。

可以使用的一个可能分数是所有预测天的 RMSE。

下面的 evaluate_forecasts() 函数将实现此行为，并根据多个七天预测返回模型的性能。

# evaluate one or more weekly forecasts against expected values
def evaluate_forecasts(actual, predicted):
	scores = list()
	# calculate an RMSE score for each day
	for i in range(actual.shape[1]):
		# calculate mse
		mse = mean_squared_error(actual[:, i], predicted[:, i])
		# calculate rmse
		rmse = sqrt(mse)
		# store
		scores.append(rmse)
	# calculate overall RMSE
	s = 0
	for row in range(actual.shape[0]):
		for col in range(actual.shape[1]):
			s += (actual[row, col] - predicted[row, col])**2
	score = sqrt(s / (actual.shape[0] * actual.shape[1]))
	return score, scores

# 针对期望值评估一个或多个每周预测

def evaluate_forecasts(actual, predicted):

scores = list()

# 计算每一天的 RMSE 分数

for i in range(actual.shape[1]):

# 计算 mse

mse = mean_squared_error(actual[:, i], predicted[:, i])

# 计算 rmse

rmse = sqrt(mse)

# 存储

scores.append(rmse)

# 计算整体 RMSE

s = 0

for row in range(actual.shape[0]):

for col in range(actual.shape[1]):

s += (actual[row, col] - predicted[row, col])**2

score = sqrt(s / (actual.shape[0] * actual.shape[1]))

return score, scores

运行函数将首先返回与日期无关的整体 RMSE，然后返回每天的 RMSE 分数数组。

训练集和测试集

我们将使用前三年的数据进行预测模型训练，并使用最后一年进行模型评估。

给定数据集中的数据将划分为标准周。这些周以周日开始，以周六结束。

这是一种现实且有用的方法，可以利用所选的模型框架，预测未来一周的电力消耗。这对于建模也很有帮助，因为模型可以用来预测特定的一天（例如星期三）或整个序列。

我们将把数据划分为标准周，从测试数据集倒序进行。

数据的最后一年是 2010 年，2010 年的第一个星期日是 1 月 3 日。数据于 2010 年 11 月中旬结束，数据中最近的最后一个星期六是 11 月 20 日。这提供了 46 周的测试数据。

下面提供了测试数据集的每日数据的起始行和结束行以供确认。

2010-01-03,2083.4539999999984,191.61000000000055,350992.12000000034,8703.600000000033,3842.0,4920.0,10074.0,15888.233355799992
...
2010-11-20,2197.006000000004,153.76800000000028,346475.9999999998,9320.20000000002,4367.0,2947.0,11433.0,17869.76663959999

2010-01-03,2083.4539999999984,191.61000000000055,350992.12000000034,8703.600000000033,3842.0,4920.0,10074.0,15888.233355799992

...

2010-11-20,2197.006000000004,153.76800000000028,346475.9999999998,9320.20000000002,4367.0,2947.0,11433.0,17869.76663959999

每日数据始于 2006 年末。

数据集中的第一个星期日是 12 月 17 日，这是数据的第二行。

将数据组织成标准周后，用于训练预测模型的完整标准周有 159 个。

2006-12-17,3390.46,226.0059999999994,345725.32000000024,14398.59999999998,2033.0,4187.0,13341.0,36946.66673200004
...
2010-01-02,1309.2679999999998,199.54600000000016,352332.8399999997,5489.7999999999865,801.0,298.0,6425.0,14297.133406600002

2006-12-17,3390.46,226.0059999999994,345725.32000000024,14398.59999999998,2033.0,4187.0,13341.0,36946.66673200004

...

2010-01-02,1309.2679999999998,199.54600000000016,352332.8399999997,5489.7999999999865,801.0,298.0,6425.0,14297.133406600002

下面的 split_dataset() 函数将每日数据拆分为训练集和测试集，并将每个数据集组织成标准周。

使用数据集的已知信息，使用特定的行偏移量来分割数据。然后使用 NumPy split() 函数将分割后的数据集组织成周数据。

# split a univariate dataset into train/test sets
def split_dataset(data):
	# split into standard weeks
	train, test = data[1:-328], data[-328:-6]
	# restructure into windows of weekly data
	train = array(split(train, len(train)/7))
	test = array(split(test, len(test)/7))
	return train, test

# 将单变量数据集拆分为训练/测试集

def split_dataset(data):

# 拆分为标准周

train, test = data[1:-328], data[-328:-6]

# 重构为每周数据的窗口

train = array(split(train, len(train)/7))

test = array(split(test, len(test)/7))

return train, test

我们可以通过加载每日数据集并打印训练集和测试集的第一行和最后一行数据来测试此函数，以确认它们符合上述预期。

完整的代码示例如下所示。

# split into standard weeks
from numpy import split
from numpy import array
from pandas import read_csv

# split a univariate dataset into train/test sets
def split_dataset(data):
	# split into standard weeks
	train, test = data[1:-328], data[-328:-6]
	# restructure into windows of weekly data
	train = array(split(train, len(train)/7))
	test = array(split(test, len(test)/7))
	return train, test

# load the new file
dataset = read_csv('household_power_consumption_days.csv', header=0, infer_datetime_format=True, parse_dates=['datetime'], index_col=['datetime'])
train, test = split_dataset(dataset.values)
# validate train data
print(train.shape)
print(train[0, 0, 0], train[-1, -1, 0])
# validate test
print(test.shape)
print(test[0, 0, 0], test[-1, -1, 0])

# 拆分为标准周

from numpy import split

from numpy import array

from pandas import read_csv

# 将单变量数据集拆分为训练/测试集

def split_dataset(data):

# 拆分为标准周

train, test = data[1:-328], data[-328:-6]

# 重构为每周数据的窗口

train = array(split(train, len(train)/7))

test = array(split(test, len(test)/7))

return train, test

# 加载新文件

dataset = read_csv('household_power_consumption_days.csv', header=0, infer_datetime_format=True, parse_dates=['datetime'], index_col=['datetime'])

train, test = split_dataset(dataset.values)

# 验证训练数据

print(train.shape)

print(train[0, 0, 0], train[-1, -1, 0])

# 验证测试数据

print(test.shape)

print(test[0, 0, 0], test[-1, -1, 0])

运行示例表明，训练集确实有 159 周的数据，而测试集有 46 周的数据。

我们可以看到，训练集和测试集的第一行和最后一行的总有功功率与我们定义为每个集合标准周边界的特定日期的数据相匹配。

(159, 7, 8)
3390.46 1309.2679999999998
(46, 7, 8)
2083.4539999999984 2197.006000000004

(159, 7, 8)

3390.46 1309.2679999999998

(46, 7, 8)

2083.4539999999984 2197.006000000004

逐时验证

模型将使用一种名为滚动预测的方案进行评估。

在这里，模型需要进行一周的预测，然后该周的实际数据将提供给模型，以便模型可以作为预测下一周的基础。这对于模型在实际中的使用方式是现实的，并且对模型有益，因为它们可以利用最佳可用数据。

我们可以在下面通过分离输入数据和输出/预测数据来演示这一点。

Input, 						Predict
[Week1]						Week2
[Week1 + Week2]				Week3
[Week1 + Week2 + Week3]		Week4
...

输入，预测

[第1周] 第2周

[第1周 + 第2周] 第3周

[第1周 + 第2周 + 第3周] 第4周

...

下面实现了使用前向验证方法来评估此数据集上的预测模型，该方法名为evaluate_model()。

作为参数“model_func”传递的是模型的函数名。该函数负责定义模型、在训练数据上拟合模型以及进行一周的预测。

然后，使用先前定义的 evaluate_forecasts() 函数，根据测试数据集评估模型所做的预测。

# evaluate a single model
def evaluate_model(model_func, train, test):
	# history is a list of weekly data
	history = [x for x in train]
	# walk-forward validation over each week
	predictions = list()
	for i in range(len(test)):
		# predict the week
		yhat_sequence = model_func(history)
		# store the predictions
		predictions.append(yhat_sequence)
		# get real observation and add to history for predicting the next week
		history.append(test[i, :])
	predictions = array(predictions)
	# evaluate predictions days for each week
	score, scores = evaluate_forecasts(test[:, :, 0], predictions)
	return score, scores

# 评估单个模型

def evaluate_model(model_func, train, test):

# 历史数据是每周数据的列表

history = [x for x in train]

# 对每一周进行前向验证

predictions = list()

for i in range(len(test)):

# 预测这一周

yhat_sequence = model_func(history)

# 存储预测结果

predictions.append(yhat_sequence)

# 获取实际观测值并添加到历史记录中，用于预测下一周

history.append(test[i, :])

predictions = array(predictions)

# 评估每周的预测天数

score, scores = evaluate_forecasts(test[:, :, 0], predictions)

return score, scores

一旦我们对模型进行了评估，我们就可以总结其性能。

下面的 *summarize_scores()* 函数将模型的性能显示为一行，以便与其他模型进行轻松比较。

# summarize scores
def summarize_scores(name, score, scores):
	s_scores = ', '.join(['%.1f' % s for s in scores])
	print('%s: [%.3f] %s' % (name, score, s_scores))

# 总结得分

def summarize_scores(name, score, scores):

s_scores = ', '.join(['%.1f' % s for s in scores])

print('%s: [%.3f] %s' % (name, score, s_scores))

我们现在拥有所有要素，可以开始评估数据集上的预测模型。

朴素预测模型

在任何新的预测问题上测试朴素预测模型非常重要。

来自朴素模型的结果提供了对预测问题难易程度的量化了解，并提供了一个基准性能，以便对更复杂的预测方法进行评估。

在本节中，我们将为家庭用电量预测问题开发和比较三种朴素预测方法；它们是：

每日持续性预测。
每周持续性预测。
周一年份之前的持续性预测。

每日持续性预测

我们将开发的第一个朴素预测是每日持续性模型。

该模型采用预测期（例如，星期六）之前最后一天的有功功率，并将其用作预测期（星期日至星期六）每天的功率值。

下面的daily_persistence() 函数实现了每日持续性预测策略。

# daily persistence model
def daily_persistence(history):
	# get the data for the prior week
	last_week = history[-1]
	# get the total active power for the last day
	value = last_week[-1, 0]
	# prepare 7 day forecast
	forecast = [value for _ in range(7)]
	return forecast

# 每日持续性模型

def daily_persistence(history):

# 获取前一周的数据

last_week = history[-1]

# 获取最后一天的总有功功率

value = last_week[-1, 0]

# 准备7天的预测

forecast = [value for _ in range(7)]

return forecast

每周持续性预测

在预测标准周时，另一个好的朴素预测方法是将整个前一周用作下一周的预测。

它基于这样的想法：下周将与本周非常相似。

下面的weekly_persistence() 函数实现了每周持续性预测策略。

# weekly persistence model
def weekly_persistence(history):
	# get the data for the prior week
	last_week = history[-1]
	return last_week[:, 0]

# 每周持续性模型

def weekly_persistence(history):

# 获取前一周的数据

last_week = history[-1]

return last_week[:, 0]

周一年份之前的持续性预测

与使用上周来预测下周的想法类似，是使用去年同期来预测下周的想法。

也就是说，使用 52 周前的观测周作为预测，基于下周将与去年同期相似的想法。

下面的week_one_year_ago_persistence() 函数实现了周一年份之前的预测策略。

# week one year ago persistence model
def week_one_year_ago_persistence(history):
	# get the data for the prior week
	last_week = history[-52]
	return last_week[:, 0]

# 周一年份之前的持续性模型

def week_one_year_ago_persistence(history):

# 获取前一周的数据

last_week = history[-52]

return last_week[:, 0]

朴素模型比较

我们可以使用上一节开发的测试框架来比较每种预测策略。

首先，可以加载数据集并将其拆分为训练集和测试集。

# load the new file
dataset = read_csv('household_power_consumption_days.csv', header=0, infer_datetime_format=True, parse_dates=['datetime'], index_col=['datetime'])
# split into train and test
train, test = split_dataset(dataset.values)

# 加载新文件

dataset = read_csv('household_power_consumption_days.csv', header=0, infer_datetime_format=True, parse_dates=['datetime'], index_col=['datetime'])

# 分割成训练集和测试集

train, test = split_dataset(dataset.values)

每种策略都可以存储在一个字典中，并用唯一的名称进行关联。此名称可用于打印和创建分数图。

# define the names and functions for the models we wish to evaluate
models = dict()
models['daily'] = daily_persistence
models['weekly'] = weekly_persistence
models['week-oya'] = week_one_year_ago_persistence

# 定义我们要评估的模型名称和函数

models = dict()

models['daily'] = daily_persistence

models['weekly'] = weekly_persistence

models['week-oya'] = week_one_year_ago_persistence

然后，我们可以枚举每种策略，使用前向验证对其进行评估，打印分数，并将分数添加到折线图中以进行可视化比较。

# evaluate each model
days = ['sun', 'mon', 'tue', 'wed', 'thr', 'fri', 'sat']
for name, func in models.items():
	# evaluate and get scores
	score, scores = evaluate_model(func, train, test)
	# summarize scores
	summarize_scores('daily persistence', score, scores)
	# plot scores
	pyplot.plot(days, scores, marker='o', label=name)

# 评估每个模型

days = ['sun', 'mon', 'tue', 'wed', 'thr', 'fri', 'sat']

for name, func in models.items():

# 评估并获取分数

score, scores = evaluate_model(func, train, test)

# 汇总分数

summarize_scores('daily persistence', score, scores)

# 绘制分数

pyplot.plot(days, scores, marker='o', label=name)

将所有这些内容联系起来，下面列出了评估三种朴素预测策略的完整示例。

# naive forecast strategies
from math import sqrt
from numpy import split
from numpy import array
from pandas import read_csv
from sklearn.metrics import mean_squared_error
from matplotlib import pyplot

# split a univariate dataset into train/test sets
def split_dataset(data):
	# split into standard weeks
	train, test = data[1:-328], data[-328:-6]
	# restructure into windows of weekly data
	train = array(split(train, len(train)/7))
	test = array(split(test, len(test)/7))
	return train, test

# evaluate one or more weekly forecasts against expected values
def evaluate_forecasts(actual, predicted):
	scores = list()
	# calculate an RMSE score for each day
	for i in range(actual.shape[1]):
		# calculate mse
		mse = mean_squared_error(actual[:, i], predicted[:, i])
		# calculate rmse
		rmse = sqrt(mse)
		# store
		scores.append(rmse)
	# calculate overall RMSE
	s = 0
	for row in range(actual.shape[0]):
		for col in range(actual.shape[1]):
			s += (actual[row, col] - predicted[row, col])**2
	score = sqrt(s / (actual.shape[0] * actual.shape[1]))
	return score, scores

# summarize scores
def summarize_scores(name, score, scores):
	s_scores = ', '.join(['%.1f' % s for s in scores])
	print('%s: [%.3f] %s' % (name, score, s_scores))

# evaluate a single model
def evaluate_model(model_func, train, test):
	# history is a list of weekly data
	history = [x for x in train]
	# walk-forward validation over each week
	predictions = list()
	for i in range(len(test)):
		# predict the week
		yhat_sequence = model_func(history)
		# store the predictions
		predictions.append(yhat_sequence)
		# get real observation and add to history for predicting the next week
		history.append(test[i, :])
	predictions = array(predictions)
	# evaluate predictions days for each week
	score, scores = evaluate_forecasts(test[:, :, 0], predictions)
	return score, scores

# daily persistence model
def daily_persistence(history):
	# get the data for the prior week
	last_week = history[-1]
	# get the total active power for the last day
	value = last_week[-1, 0]
	# prepare 7 day forecast
	forecast = [value for _ in range(7)]
	return forecast

# weekly persistence model
def weekly_persistence(history):
	# get the data for the prior week
	last_week = history[-1]
	return last_week[:, 0]

# week one year ago persistence model
def week_one_year_ago_persistence(history):
	# get the data for the prior week
	last_week = history[-52]
	return last_week[:, 0]

# load the new file
dataset = read_csv('household_power_consumption_days.csv', header=0, infer_datetime_format=True, parse_dates=['datetime'], index_col=['datetime'])
# split into train and test
train, test = split_dataset(dataset.values)
# define the names and functions for the models we wish to evaluate
models = dict()
models['daily'] = daily_persistence
models['weekly'] = weekly_persistence
models['week-oya'] = week_one_year_ago_persistence
# evaluate each model
days = ['sun', 'mon', 'tue', 'wed', 'thr', 'fri', 'sat']
for name, func in models.items():
	# evaluate and get scores
	score, scores = evaluate_model(func, train, test)
	# summarize scores
	summarize_scores(name, score, scores)
	# plot scores
	pyplot.plot(days, scores, marker='o', label=name)
# show plot
pyplot.legend()
pyplot.show()

100

101

102

# 朴素预测策略

from math import sqrt

from numpy import split

from numpy import array

from pandas import read_csv

from sklearn.metrics import mean_squared_error

from matplotlib import pyplot

# 将单变量数据集拆分为训练/测试集

def split_dataset(data):

# 拆分为标准周

train, test = data[1:-328], data[-328:-6]

# 重构为每周数据的窗口

train = array(split(train, len(train)/7))

test = array(split(test, len(test)/7))

return train, test

# 针对期望值评估一个或多个每周预测

def evaluate_forecasts(actual, predicted):

scores = list()

# 计算每一天的 RMSE 分数

for i in range(actual.shape[1]):

# 计算 mse

mse = mean_squared_error(actual[:, i], predicted[:, i])

# 计算 rmse

rmse = sqrt(mse)

# 存储

scores.append(rmse)

# 计算整体 RMSE

s = 0

for row in range(actual.shape[0]):

for col in range(actual.shape[1]):

s += (actual[row, col] - predicted[row, col])**2

score = sqrt(s / (actual.shape[0] * actual.shape[1]))

return score, scores

# 总结得分

def summarize_scores(name, score, scores):

s_scores = ', '.join(['%.1f' % s for s in scores])

print('%s: [%.3f] %s' % (name, score, s_scores))

# 评估单个模型

def evaluate_model(model_func, train, test):

# 历史数据是每周数据的列表

history = [x for x in train]

# 对每一周进行前向验证

predictions = list()

for i in range(len(test)):

# 预测这一周

yhat_sequence = model_func(history)

# 存储预测结果

predictions.append(yhat_sequence)

# 获取实际观测值并添加到历史记录中，用于预测下一周

history.append(test[i, :])

predictions = array(predictions)

# 评估每周的预测天数

score, scores = evaluate_forecasts(test[:, :, 0], predictions)

return score, scores

# 每日持续性模型

def daily_persistence(history):

# 获取前一周的数据

last_week = history[-1]

# 获取最后一天的总有功功率

value = last_week[-1, 0]

# 准备7天的预测

forecast = [value for _ in range(7)]

return forecast

# 每周持续性模型

def weekly_persistence(history):

# 获取前一周的数据

last_week = history[-1]

return last_week[:, 0]

# 周一年份之前的持续性模型

def week_one_year_ago_persistence(history):

# 获取前一周的数据

last_week = history[-52]

return last_week[:, 0]

# 加载新文件

dataset = read_csv('household_power_consumption_days.csv', header=0, infer_datetime_format=True, parse_dates=['datetime'], index_col=['datetime'])

# 分割成训练集和测试集

train, test = split_dataset(dataset.values)

# 定义我们要评估的模型名称和函数

models = dict()

models['daily'] = daily_persistence

models['weekly'] = weekly_persistence

models['week-oya'] = week_one_year_ago_persistence

# 评估每个模型

days = ['sun', 'mon', 'tue', 'wed', 'thr', 'fri', 'sat']

for name, func in models.items():

# 评估并获取分数

score, scores = evaluate_model(func, train, test)

# 汇总分数

summarize_scores(name, score, scores)

# 绘制分数

pyplot.plot(days, scores, marker='o', label=name)

# 显示图

pyplot.legend()

pyplot.show()

运行示例首先会打印每个模型的总分和每日分。

我们可以看到，每周策略的性能优于每日策略，而“去年同一周”（week-oya）的性能又略好一些。

注意：您获得的结果可能会有所不同，这取决于算法或评估过程的随机性，或者数值精度的差异。考虑多次运行示例并比较平均结果。

我们可以看到，每个模型的总体 RMSE 分数和每个预测日的每日分数都体现了这一点。一个例外是第一天（星期日）的预测误差，其中每日持续模型似乎优于两个每周策略。

我们可以将“去年同一周”策略的总体 RMSE（465.294 千瓦）作为基线性能，供我们在该特定问题框架下考虑更复杂的模型。

daily: [511.886] 452.9, 596.4, 532.1, 490.5, 534.3, 481.5, 482.0
weekly: [469.389] 567.6, 500.3, 411.2, 466.1, 471.9, 358.3, 482.0
week-oya: [465.294] 550.0, 446.7, 398.6, 487.0, 459.3, 313.5, 555.1

每日：[511.886] 452.9、596.4、532.1、490.5、534.3、481.5、482.0

每周：[469.389] 567.6、500.3、411.2、466.1、471.9、358.3、482.0

去年同一周：[465.294] 550.0、446.7、398.6、487.0、459.3、313.5、555.1

还会创建一个每日预测误差的折线图。

我们可以看到，与每日策略相比，每周策略通常表现更好，除了第一天的情况。

对我来说，去年同一周的表现优于使用前一周的表现，这令人惊讶。我原本以为上周的电力消耗会更相关。

在同一张图上审视所有策略，提示了可能将这些策略组合起来以获得更好性能的方法。

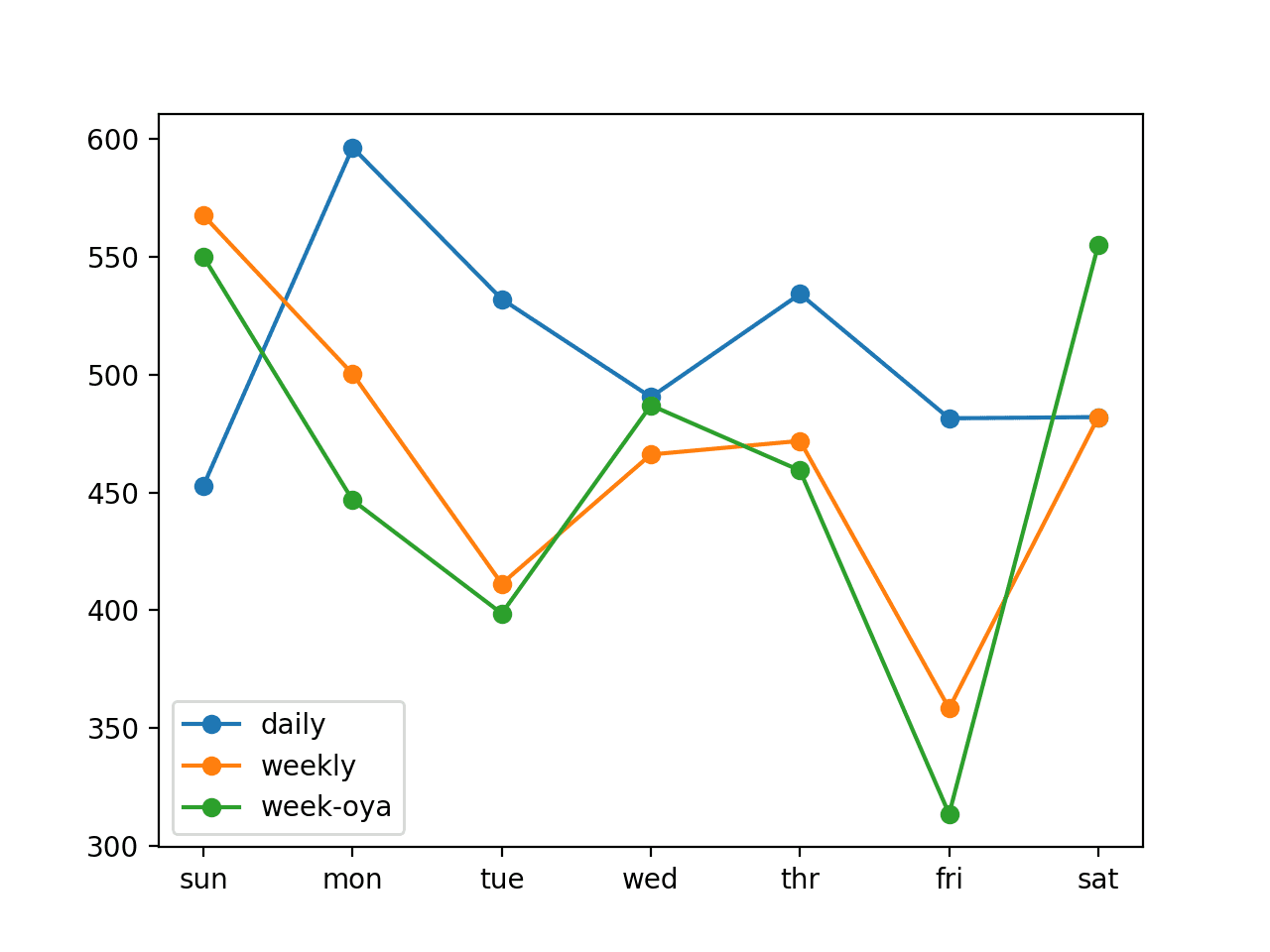
Line Plot Comparing Naive Forecast Strategies for Household Power Forecasting

家庭电力预测朴素策略比较折线图

扩展

本节列出了一些您可能希望探索的扩展本教程的想法。

附加朴素策略。为预测下一周的电力消耗提出、开发和评估一种额外的朴素策略。
朴素集成策略。开发一种集成策略，结合三种提出的朴素预测方法的预测。
优化直接持续模型。测试并为直接持续模型中的每个预测日找到最佳的相对前一天（例如 -1 或 -7）。

如果您探索了这些扩展中的任何一个，我很想知道。

进一步阅读

如果您想深入了解，本节提供了更多关于该主题的资源。

API

文章

总结

在本教程中，您学习了如何为家庭电力消耗数据集开发测试框架，并评估了三种朴素预测策略，为更复杂的算法提供了基线。

具体来说，你学到了：

如何加载、准备和降采样家庭电力消耗数据集，使其适合建模。
如何开发指标、数据集拆分以及前向验证元素，为评估预测模型构建强大的测试框架。
如何开发、评估和比较一系列朴素的持续性预测方法的性能。

你有什么问题吗？
在下面的评论中提出你的问题，我会尽力回答。

关于此主题的更多信息

如何加载和探索家庭用电数据

家庭用电量的自回归预测模型

评估家庭用电量预测的朴素模型的 23 条回复

sanjie 2018 年 10 月 3 日 12:38 am #

你好，杰森，
您的文章对我们学习 ML 和 DL 非常有帮助。
您是否有关于强化学习的文章，例如 Sarsa、Q learning、Monte-carlo learning、Deep-Q-Network 等？

非常感谢。

回复
- Jason Brownlee 2018 年 10 月 3 日 6:19 am #
  
  目前还没有，我不认为它们除了玩具问题之外还有什么用处（例如，我认为开发人员无法在“工作中”使用这些方法）。
  
  回复
Nayan 2018 年 10 月 3 日 4:18 am #

嗨，Jason！
我目前正在做一个 NMT 项目，用于翻译我的母语和英语之间的互译。按照我的项目导师的说法，我使用 openNMT 包附带的默认自述文件生成了 20 个 epoch。现在我被要求再生成 80 个 epoch。他告诉我这可以通过 start_index 和 end_index 来实现。我搜索了很多如何做到这一点的方法，最终找到了这个
https://machinelearning.org.cn/text-generation-lstm-recurrent-neural-networks-python-keras/

请指导我如何做到这一点！
谢谢你

回复
- Jason Brownlee 2018 年 10 月 3 日 6:23 am #
  
  抱歉，我没有关于 openNMT 的资料，我无法提供好的即时建议。
  
  回复
  - Nayan 2018 年 10 月 3 日 6:47 pm #
    
    好的！
    谢谢您的回复
    
    回复
sanjie 2018 年 10 月 3 日 9:54 am #

感谢您的回复。
祝您有美好的一天。

回复
- Jason Brownlee 2018 年 10 月 3 日 4:13 pm #
  
  不客气。
  
  回复
Allan 2018 年 10 月 9 日 11:49 am #

很棒的文章（和系列）。谢谢。有 R 语言版本的代码吗？

回复
- Jason Brownlee 2018 年 10 月 9 日 3:05 pm #
  
  谢谢。
  
  没有，抱歉，我目前专注于 Python，因为需求更大。
  
  回复

mk 2019 年 1 月 9 日 6:52 pm #

将数据集转换为 household_power_consumption_hour
我使用了您的代码。
六小时为一个“基准”，就像七天为一个星期一样。
我这样理解正确吗？

# daily persistence model
def daily_persistence(history):
	# get the data for the prior week
	last_week = history[-1]
	# get the total active power for the last day
	value = last_week[-1, 0]
	# prepare 6 hours forecast
	forecast = [value for _ in range(6)]
	return forecast

# 每日持续性模型

def daily_persistence(history):

# 获取前一周的数据

last_week = history[-1]

# 获取最后一天的总有功功率

value = last_week[-1, 0]

# 准备 6 小时预测

forecast = [value for _ in range(6)]

return forecast

谢谢

Jason Brownlee 2019 年 1 月 10 日 7:48 am #

抱歉，我没有能力调试您的更改。

回复

KG 2019 年 2 月 28 日 5:56 pm #

你好！我现在想做一个功率放大器的模型。功率放大器的输入和输出都是由实部和虚部组成的复数。现在我有输入和输出的数据。如何处理这些数据？非常感谢！

回复
- Jason Brownlee 2019 年 3 月 1 日 6:15 am #
  
  也许可以尝试一系列表示和模型，看看哪种最适合您的特定数据集，这可能会有帮助。
  https://machinelearning.org.cn/faq/single-faq/what-algorithm-config-should-i-use
  
  回复
Darshittaa 2019 年 8 月 21 日 6:23 pm #

您能否详细说明朴素贝叶斯算法的应用结论？

回复
- Jason Brownlee 2019 年 8 月 22 日 6:24 am #
  
  本教程中没有使用朴素贝叶斯。
  
  回复
Nicholas Jallan 2020 年 4 月 6 日 8:53 pm #

总体 RMSE 可以用以下公式计算：
”’python
score = np.sqrt(np.mean((actual-predicted)**2))
”’
为了清晰起见，数据集应仅保留将要预测的值（并删除所有其他列），并且仅操作 numpy 数组（而不是列表）。

一个很好的附加图是显示一段时间内的预测和真实基线。
此致

回复
- Jason Brownlee 2020 年 4 月 7 日 5:47 am #
  
  谢谢。
  
  回复
William Amador 2020 年 4 月 9 日 7:15 am #

非常好的贡献，一个问题是，如果我的感兴趣的预测变量是电压，作为一种调整，以便在预测中它将此值作为输出。

感谢您的合作

回复
- Jason Brownlee 2020 年 4 月 9 日 8:10 am #
  
  抱歉，我不明白您的问题，也许您可以重述一下？
  
  回复
  - William Amador 2020 年 4 月 9 日 9:37 am #
    
    如何更改代码中的预测变量？
    在这种情况下，选择数据集中的另一个变量（电压）
    
    回复
    - Jason Brownlee 2020 年 4 月 9 日 1:13 pm #
      
      也许可以关注“加载和准备数据集”部分。
      
      这应该相当直接，如果不行，也许可以从一些更简单的教程开始，以熟悉 Python 编程。
      
      回复
Sarah Alhrbi 2020 年 6 月 3 日 6:27 pm #

嗨，Jason，

感谢这个很棒的教程，

关于数据集的重塑方式，有些地方我没能理解。实际上，我在您的大部分教程中都遇到了这个问题。我相信我误解了某个要点。

所以，数据分割后的形状如下：训练集：(159, 7, 8)，测试集：(46, 7, 8)

那么预测的形状将是 (46, 7, 1)？对吗？
如果是这样，这意味着预测的点比需要的要多，不是吗？

我尝试绘制结果时得到了一些奇怪的东西。我不确定为什么！

这是它的样子：

我https://www.dropbox.com/s/8jblxjhxmtfjcip/Screen%20Shot%202020-06-03%20at%206.23.29%20pm.png?dl=0

您的反馈对我非常有价值。

还有一个问题，如果我想购买您的某本书，是否有折扣？

此致，

回复
- Jason Brownlee 2020 年 6 月 4 日 6:13 am #
  
  LSTM 的输入形状可能令人困惑，这会有帮助。
  https://machinelearning.org.cn/faq/single-faq/what-is-the-difference-between-samples-timesteps-and-features-for-lstm-input
  
  回复

导航

评估用于预测家庭用电量的朴素模型

教程概述

问题描述

加载并准备数据集

时间序列深度学习需要帮助吗？

模型评估

问题构建

评估指标

训练集和测试集

逐时验证

朴素预测模型

每日持续性预测

每周持续性预测

周一年份之前的持续性预测

朴素模型比较

扩展

进一步阅读

API

文章

总结

立即开发时间序列深度学习模型！

在几分钟内开发您自己的预测模型

最终将深度学习应用于您的时间序列预测项目

关于此主题的更多信息

评估家庭用电量预测的朴素模型的 23 条回复

留下回复点击这里取消回复。

导航

教程概述

问题描述

加载并准备数据集

时间序列深度学习需要帮助吗？

模型评估

问题构建

评估指标

训练集和测试集

逐时验证

朴素预测模型

每日持续性预测

每周持续性预测

周一年份之前的持续性预测

朴素模型比较

扩展

进一步阅读

API

文章

总结

立即开发时间序列深度学习模型！

在几分钟内开发您自己的预测模型

最终将深度学习应用于您的时间序列预测项目

关于此主题的更多信息

评估家庭用电量预测的朴素模型 的 23 条回复

留下回复 点击这里取消回复。

评估家庭用电量预测的朴素模型的 23 条回复

留下回复点击这里取消回复。