为新的数据集开发神经网络预测模型可能具有挑战性。
一种方法是首先检查数据集并构思可能适用的模型,然后探索简单模型在数据集上的学习动态,最后使用健壮的测试框架开发和调整模型以适应数据集。
这个过程可以用于开发有效的神经网络模型,用于分类和回归预测建模问题。
在本教程中,您将学习如何为癌症生存二元分类数据集开发多层感知器神经网络模型。
完成本教程后,您将了解:
- 如何加载和总结癌症生存数据集,并利用结果提出数据准备和模型配置建议。
- 如何探索简单MLP模型在数据集上的学习动态。
- 如何开发模型性能的稳健估计,调整模型性能并对新数据进行预测。
让我们开始吧。

为癌症生存数据集开发一个神经网络
照片由 Bernd Thaller 提供,部分权利保留。
教程概述
本教程分为4个部分,它们是:
- Haberman 乳腺癌生存数据集
- 神经网络学习动态
- 稳健的模型评估
- 最终模型及预测
Haberman 乳腺癌生存数据集
第一步是定义和探索数据集。
我们将使用“haberman”标准二元分类数据集。
该数据集描述了乳腺癌患者数据,结果是患者的生存情况。具体来说,患者是否生存了五年或更长时间,或者是否未生存。
这是不平衡分类研究中的一个标准数据集。根据数据集的描述,这些手术于1958年至1970年间在芝加哥大学 Billings 医院进行。
数据集中有306个样本,有3个输入变量;它们是:
- 患者手术时的年龄。
- 手术的两位数年份。
- 检测到的“阳性腋窝淋巴结”数量,这是衡量癌症是否扩散的指标。
因此,除了数据集中可用的信息外,我们无法控制构成数据集的案例选择或在这些案例中使用哪些特征。
尽管该数据集描述了乳腺癌患者的生存情况,但考虑到数据集规模小,并且数据基于几十年前的乳腺癌诊断和手术,因此在该数据集上构建的模型预计不会有泛化能力。
注意:为求清楚明了,我们 不是 在“解决乳腺癌”。我们正在研究一个标准分类数据集。
下面是数据集中前 5 行的样本
|
1 2 3 4 5 6 |
30,64,1,1 30,62,3,1 30,65,0,1 31,59,2,1 31,65,4,1 ... |
你可以在此处了解更多关于此数据集的信息:
我们可以直接从 URL 将数据集加载为 pandas DataFrame;例如:
|
1 2 3 4 5 6 7 8 |
# 加载 haberman 数据集并总结其形状 from pandas import read_csv # 定义数据集位置 url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/haberman.csv' # 加载数据集 df = read_csv(url, header=None) # 总结形状 print(df.shape) |
运行示例将直接从 URL 加载数据集并报告数据集的形状。
在这种情况下,我们可以确认数据集有4个变量(3个输入和1个输出),并且数据集有306行数据。
对于神经网络来说,这并不算很多行数据,这表明使用小型网络,可能带有正则化,会是比较合适的。
这还表明,使用 k 折交叉验证是个好主意,因为它能比训练/测试分割提供更可靠的模型性能估计,并且一个模型可以在几秒钟内完成训练,而不是像大型数据集那样需要数小时或数天。
|
1 |
(306, 4) |
接下来,我们可以通过查看摘要统计信息和数据图来进一步了解数据集。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# 显示 haberman 数据集的统计摘要和图表 from pandas import read_csv from matplotlib import pyplot # 定义数据集位置 url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/haberman.csv' # 加载数据集 df = read_csv(url, header=None) # 显示摘要统计信息 print(df.describe()) # plot histograms df.hist() pyplot.show() |
运行示例首先加载数据,然后打印每个变量的摘要统计信息。
我们可以看到值具有不同的均值和标准差,可能在建模之前需要进行一些归一化或标准化。
|
1 2 3 4 5 6 7 8 9 |
0 1 2 3 count 306.000000 306.000000 306.000000 306.000000 mean 52.457516 62.852941 4.026144 1.264706 std 10.803452 3.249405 7.189654 0.441899 min 30.000000 58.000000 0.000000 1.000000 25% 44.000000 60.000000 0.000000 1.000000 50% 52.000000 63.000000 1.000000 1.000000 75% 60.750000 65.750000 4.000000 2.000000 max 83.000000 69.000000 52.000000 2.000000 |
然后为每个变量创建直方图。
我们可以看到,第一个变量可能是高斯分布,而接下来的两个输入变量可能是指数分布。
我们可能可以通过对每个变量使用幂变换来获得一些好处,以使概率分布的偏斜程度降低,这可能会提高模型性能。
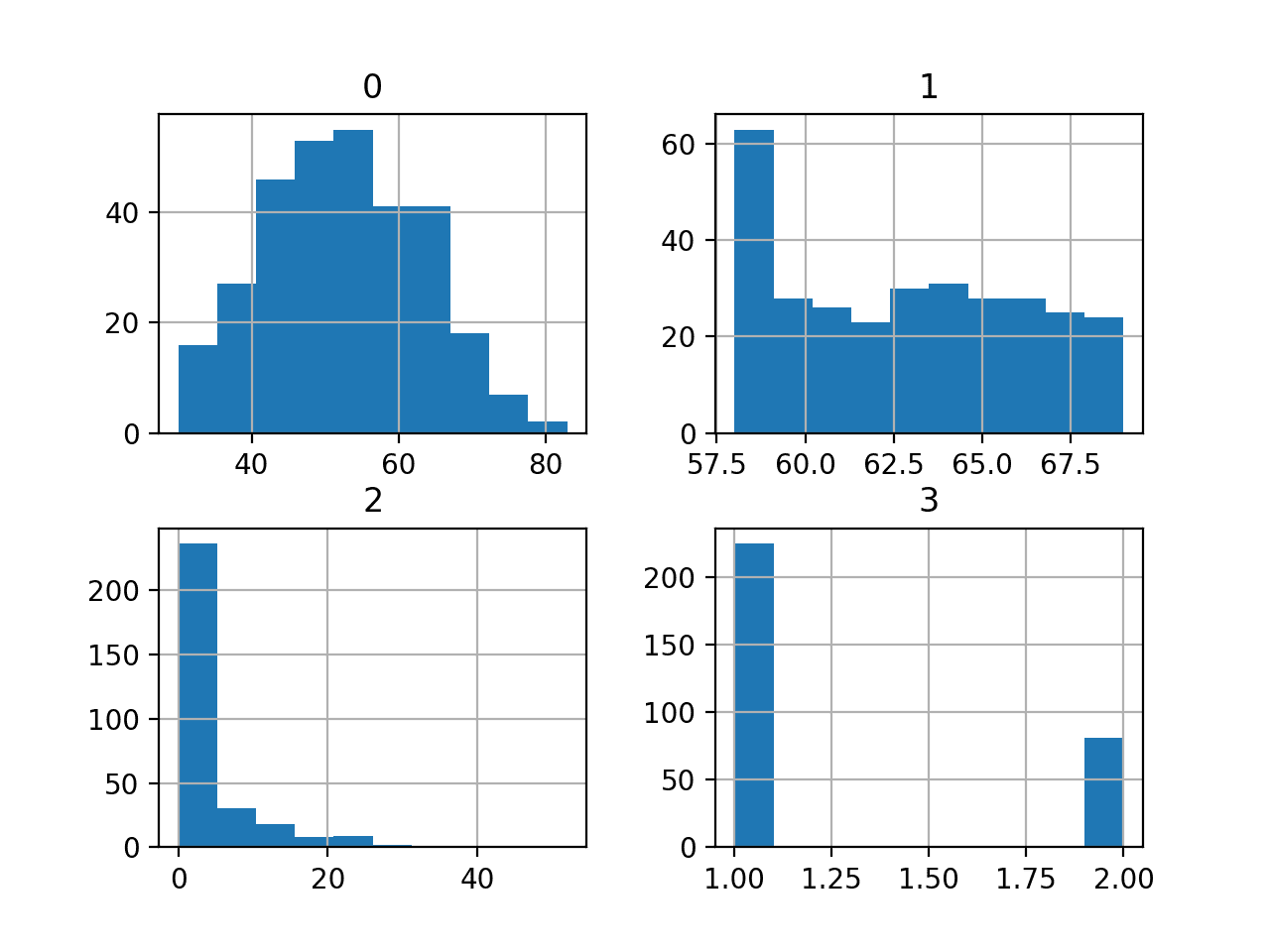
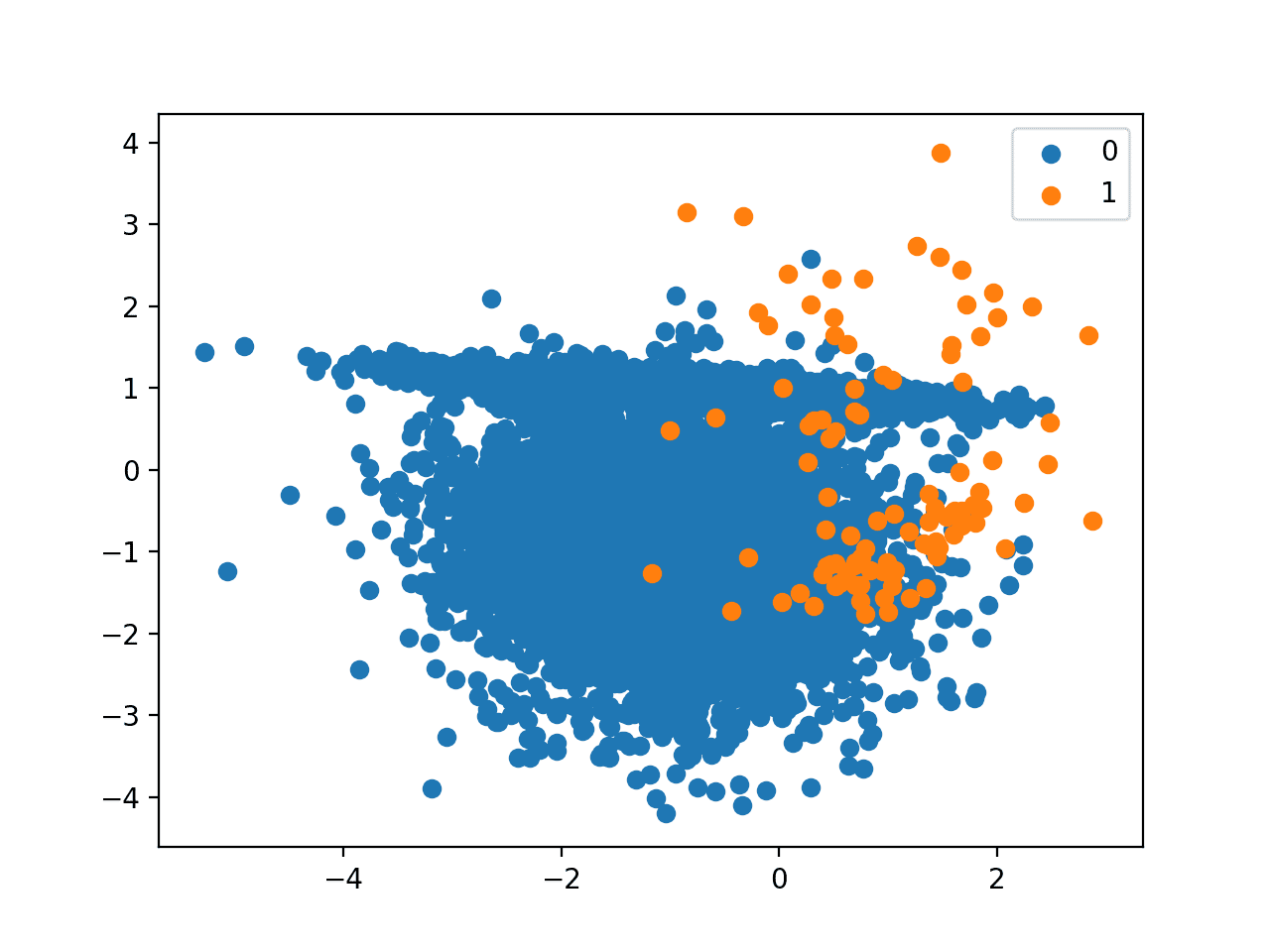
Haberman 乳腺癌生存分类数据集的直方图
我们可以看到两个类别之间的样本分布存在一些偏斜,这意味着分类问题是不平衡的。它是倾斜的。
了解数据集的实际不平衡程度可能会有所帮助。
我们可以使用 Counter 对象来计算每个类别的样本数量,然后利用这些数量来总结分布。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
# 总结 haberman 数据集的类别比例 from pandas import read_csv from collections import Counter # 定义数据集位置 url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/haberman.csv' # 定义数据集列名 columns = ['age', 'year', 'nodes', 'class'] # 将csv文件加载为数据框 dataframe = read_csv(url, header=None, names=columns) # 总结类别分布 target = dataframe['class'].values counter = Counter(target) for k,v in counter.items(): per = v / len(target) * 100 print('Class=%d, Count=%d, Percentage=%.3f%%' % (k, v, per)) |
运行示例可以总结数据集的类别分布。
我们可以看到,生存类别1的样本最多,为225个,占数据集的74%左右。非生存类别2的样本较少,为81个,占数据集的26%左右。
类别分布是倾斜的,但并不严重不平衡。
|
1 2 |
Class=1, Count=225, Percentage=73.529% Class=2, Count=81, Percentage=26.471% |
这很有帮助,因为如果我们使用分类准确率,那么任何准确率低于73.5%的模型在这个数据集上都没有技能。
现在我们熟悉了数据集,让我们探索一下如何开发神经网络。
神经网络学习动态
我们将使用 TensorFlow 为该数据集开发多层感知器 (MLP) 模型。
我们无法知道什么模型架构或学习超参数最适合这个数据集,因此我们必须进行实验和探索,找出有效的方法。
考虑到数据集较小,使用较小的批次大小可能是个好主意,例如16或32行。在开始时,使用随机梯度下降的 Adam 版本是个好主意,因为它会自动调整学习率,并且在大多数数据集上效果很好。
在我们认真评估模型之前,最好回顾学习动态并调整模型架构和学习配置,直到我们获得稳定的学习动态,然后再考虑如何充分利用模型。
我们可以通过使用简单训练/测试分割数据并查看学习曲线图来实现这一点。这将帮助我们了解是否出现过拟合或欠拟合;然后我们可以相应地调整配置。
首先,我们必须确保所有输入变量都是浮点值,并将目标标签编码为整数值 0 和 1。
|
1 2 3 4 5 |
... # 确保所有数据都是浮点值 X = X.astype('float32') # 将字符串编码为整数 y = LabelEncoder().fit_transform(y) |
接下来,我们可以将数据集分割为输入和输出变量,然后分割为 67/33 的训练集和测试集。
我们必须确保分割是按类别分层的,以确保训练集和测试集具有与主数据集相同的类别标签分布。
|
1 2 3 4 5 |
... # 分割成输入和输出列 X, y = df.values[:, :-1], df.values[:, -1] # 分割为训练集和测试集 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, stratify=y, random_state=3) |
我们可以定义一个最小的 MLP 模型。在这种情况下,我们将使用一个具有10个节点的隐藏层和一个输出层(任意选择)。我们将在隐藏层中使用 ReLU 激活函数 和“he_normal” 权重初始化,因为这两者结合起来是一个好的实践。
模型的输出是用于二元分类的 sigmoid 激活,我们将最小化二元 交叉熵损失。
|
1 2 3 4 5 6 7 8 9 |
... # 确定输入特征的数量 n_features = X.shape[1] # 定义模型 model = Sequential() model.add(Dense(10, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,))) model.add(Dense(1, activation='sigmoid')) # 编译模型 model.compile(optimizer='adam', loss='binary_crossentropy') |
我们将为模型拟合200个训练周期(任意选择),批次大小为16,因为这是一个小数据集。
我们使用原始数据来拟合模型,我们认为这可能是个好主意,但这只是一个重要的起点。
|
1 2 3 |
... # 拟合模型 history = model.fit(X_train, y_train, epochs=200, batch_size=16, verbose=0, validation_data=(X_test,y_test)) |
训练结束后,我们将评估模型在测试集上的性能,并报告分类准确率作为性能指标。
|
1 2 3 4 5 6 |
... # 预测测试集 yhat = model.predict_classes(X_test) # 评估预测 score = accuracy_score(y_test, yhat) print('Accuracy: %.3f' % score) |
最后,我们将绘制训练过程中训练集和测试集上交叉熵损失的学习曲线。
|
1 2 3 4 5 6 7 8 9 |
... # 绘制学习曲线 pyplot.title('学习曲线') pyplot.xlabel('Epoch') pyplot.ylabel('交叉熵') pyplot.plot(history.history['loss'], label='train') pyplot.plot(history.history['val_loss'], label='val') pyplot.legend() pyplot.show() |
将所有内容汇总起来,下面是评估我们在癌症生存数据集上的第一个 MLP 的完整示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
# 在 haberman 数据集上拟合简单的 mlp 模型并查看学习曲线 from pandas import read_csv from sklearn.model_selection import train_test_split from sklearn.preprocessing import LabelEncoder from sklearn.metrics import accuracy_score from tensorflow.keras import Sequential from tensorflow.keras.layers import Dense from matplotlib import pyplot # 加载数据集 path = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/haberman.csv' df = read_csv(path, header=None) # 分割成输入和输出列 X, y = df.values[:, :-1], df.values[:, -1] # 确保所有数据都是浮点值 X = X.astype('float32') # 将字符串编码为整数 y = LabelEncoder().fit_transform(y) # 分割为训练集和测试集 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, stratify=y, random_state=3) # 确定输入特征的数量 n_features = X.shape[1] # 定义模型 model = Sequential() model.add(Dense(10, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,))) model.add(Dense(1, activation='sigmoid')) # 编译模型 model.compile(optimizer='adam', loss='binary_crossentropy') # 拟合模型 history = model.fit(X_train, y_train, epochs=200, batch_size=16, verbose=0, validation_data=(X_test,y_test)) # 预测测试集 yhat = model.predict_classes(X_test) # 评估预测 score = accuracy_score(y_test, yhat) print('Accuracy: %.3f' % score) # 绘制学习曲线 pyplot.title('学习曲线') pyplot.xlabel('Epoch') pyplot.ylabel('交叉熵') pyplot.plot(history.history['loss'], label='train') pyplot.plot(history.history['val_loss'], label='val') pyplot.legend() pyplot.show() |
运行示例首先在训练数据集上拟合模型,然后报告测试数据集上的分类准确率。
使用我的新书 机器学习数据准备 快速启动您的项目,其中包含分步教程以及所有示例的Python源代码文件。
在这种情况下,我们可以看到模型表现优于无技能模型,因为准确率高于约 73.5%。
|
1 |
Accuracy: 0.765 |
然后创建训练集和测试集上损失的学习曲线图。
我们可以看到,模型可以快速在数据集上找到一个好的拟合,并且似乎没有过拟合或欠拟合。
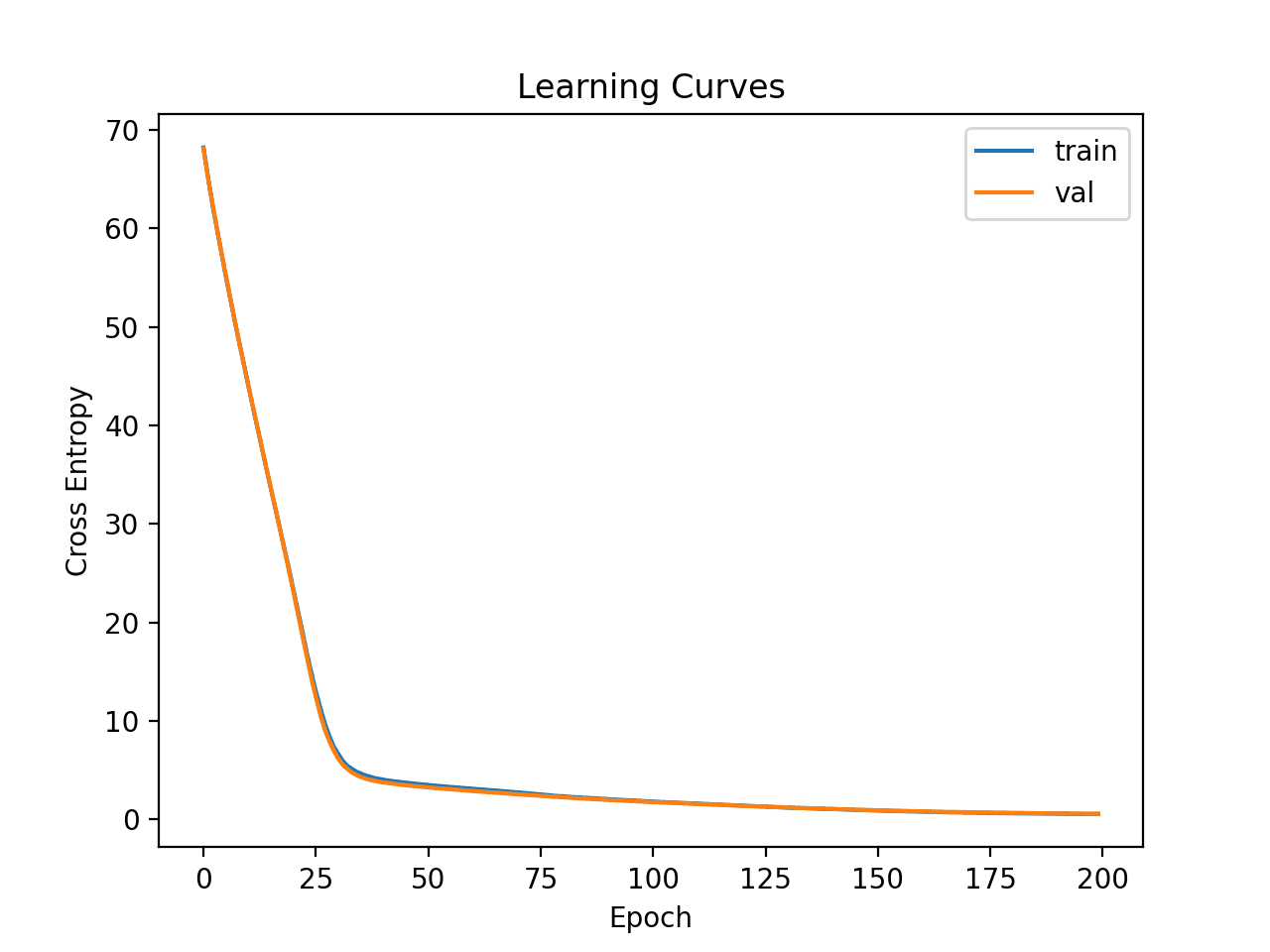
简单多层感知器在癌症生存数据集上的学习曲线
现在我们对简单 MLP 模型在数据集上的学习动态有了一些了解,我们可以着手开发更稳健的模型性能评估。
稳健的模型评估
k 折交叉验证过程可以提供更可靠的 MLP 性能估计,尽管它可能非常耗时。
这是因为必须拟合和评估 k 个模型。当数据集规模很小时,例如癌症生存数据集,这不是问题。
我们可以使用 StratifiedKFold 类并手动枚举每个折叠,拟合模型,对其进行评估,然后在过程结束时报告评估分数的平均值。
|
1 2 3 4 5 6 7 8 9 10 11 |
... # 准备交叉验证 kfold = KFold(10) # 枚举划分 scores = list() for train_ix, test_ix in kfold.split(X, y): # 拟合和评估模型... ... ... # 汇总所有分数 print('Mean Accuracy: %.3f (%.3f)' % (mean(scores), std(scores))) |
我们可以使用这个框架来为基础配置开发可靠的 MLP 模型性能估计,甚至可以针对一系列不同的数据准备、模型架构和学习配置进行评估。
在上一节中,我们在数据集上理解了模型的学习动态,这在进行 k 折交叉验证以估计性能之前很重要。如果我们直接开始调整模型,我们可能会得到好的结果,但如果没有,我们可能不知道原因,例如模型过拟合或欠拟合。
如果我们再次对模型进行大的更改,最好回到并确认模型正在正确收敛。
下面列出了使用此框架评估上一节中基础 MLP 模型的完整示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 |
# haberman 数据集的基线模型的 k 折交叉验证 from numpy import mean from numpy import std from pandas import read_csv from sklearn.model_selection import StratifiedKFold from sklearn.preprocessing import LabelEncoder from sklearn.metrics import accuracy_score from tensorflow.keras import Sequential from tensorflow.keras.layers import Dense from matplotlib import pyplot # 加载数据集 path = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/haberman.csv' df = read_csv(path, header=None) # 分割成输入和输出列 X, y = df.values[:, :-1], df.values[:, -1] # 确保所有数据都是浮点值 X = X.astype('float32') # 将字符串编码为整数 y = LabelEncoder().fit_transform(y) # 准备交叉验证 kfold = StratifiedKFold(10, random_state=1) # 枚举划分 scores = list() for train_ix, test_ix in kfold.split(X, y): # 分割数据 X_train, X_test, y_train, y_test = X[train_ix], X[test_ix], y[train_ix], y[test_ix] # 确定输入特征的数量 n_features = X.shape[1] # 定义模型 model = Sequential() model.add(Dense(10, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,))) model.add(Dense(1, activation='sigmoid')) # 编译模型 model.compile(optimizer='adam', loss='binary_crossentropy') # 拟合模型 model.fit(X_train, y_train, epochs=200, batch_size=16, verbose=0) # 预测测试集 yhat = model.predict_classes(X_test) # 评估预测结果 score = accuracy_score(y_test, yhat) print('>%.3f' % score) scores.append(score) # 汇总所有分数 print('Mean Accuracy: %.3f (%.3f)' % (mean(scores), std(scores))) |
运行示例将报告每次评估过程的模型的性能,并在运行结束时报告分类准确率的平均值和标准差。
使用我的新书 机器学习数据准备 快速启动您的项目,其中包含分步教程以及所有示例的Python源代码文件。
在这种情况下,我们可以看到 MLP 模型达到了约 75.2% 的平均准确率,这与我们在上一节中的粗略估计非常接近。
这证实了我们的预期,即基线模型配置可能比该数据集的朴素模型效果更好。
|
1 2 3 4 5 6 7 8 9 10 11 |
>0.742 >0.774 >0.774 >0.806 >0.742 >0.710 >0.767 >0.800 >0.767 >0.633 Mean Accuracy: 0.752 (0.048) |
这是一个好结果吗?
事实上,这是一个具有挑战性的分类问题,达到约 74.5% 以上的分数是很好的。
接下来,我们看看如何拟合最终模型并使用它来做出预测。
最终模型及预测
选择模型配置后,我们可以使用所有可用数据训练最终模型,并用它来对新数据进行预测。
在此案例中,我们将使用带有 dropout 和小型批次大小的模型作为我们的最终模型。
我们可以像以前一样准备数据并拟合模型,但这次是在整个数据集上,而不是在一个训练子集上。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
... # 分割成输入和输出列 X, y = df.values[:, :-1], df.values[:, -1] # 确保所有数据都是浮点值 X = X.astype('float32') # 将字符串编码为整数 le = LabelEncoder() y = le.fit_transform(y) # 确定输入特征的数量 n_features = X.shape[1] # 定义模型 model = Sequential() model.add(Dense(10, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,))) model.add(Dense(1, activation='sigmoid')) # 编译模型 model.compile(optimizer='adam', loss='binary_crossentropy') |
然后,我们可以使用此模型对新数据进行预测。
首先,我们可以定义一个新数据行。
|
1 2 3 |
... # 定义一行新数据 row = [30,64,1] |
注意:我从数据集中第一行取了一行,期望的标签是“1”。
然后我们可以进行预测。
|
1 2 3 |
... # 进行预测 yhat = model.predict_classes([row]) |
然后对预测结果进行逆变换,以便我们可以使用或解释正确标签下的结果(对于此数据集,它只是一个整数)。
|
1 2 3 |
... # 逆变换以获得类别标签 yhat = le.inverse_transform(yhat) |
在这种情况下,我们将只报告预测结果。
|
1 2 3 |
... # 报告预测结果 print('Predicted: %s' % (yhat[0])) |
将所有内容汇总起来,下面是为 haberman 数据集拟合最终模型并使用它来预测新数据的完整示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
# 为 haberman 数据集拟合最终模型并对新数据进行预测 from pandas import read_csv from sklearn.preprocessing import LabelEncoder from sklearn.metrics import accuracy_score from tensorflow.keras import Sequential from tensorflow.keras.layers import Dense from tensorflow.keras.layers import Dropout # 加载数据集 path = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/haberman.csv' df = read_csv(path, header=None) # 分割成输入和输出列 X, y = df.values[:, :-1], df.values[:, -1] # 确保所有数据都是浮点值 X = X.astype('float32') # 将字符串编码为整数 le = LabelEncoder() y = le.fit_transform(y) # 确定输入特征的数量 n_features = X.shape[1] # 定义模型 model = Sequential() model.add(Dense(10, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,))) model.add(Dense(1, activation='sigmoid')) # 编译模型 model.compile(optimizer='adam', loss='binary_crossentropy') # 拟合模型 model.fit(X, y, epochs=200, batch_size=16, verbose=0) # 定义一行新数据 row = [30,64,1] # 进行预测 yhat = model.predict_classes([row]) # 逆变换以获得类别标签 yhat = le.inverse_transform(yhat) # 报告预测结果 print('Predicted: %s' % (yhat[0])) |
运行示例会将模型拟合到整个数据集,并为新数据的单行进行预测。
使用我的新书 机器学习数据准备 快速启动您的项目,其中包含分步教程以及所有示例的Python源代码文件。
在这种情况下,我们可以看到模型为输入行预测了“1”标签。
|
1 |
Predicted: 1 |
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
教程
总结
在本教程中,您学习了如何为癌症生存二元分类数据集开发多层感知器神经网络模型。
具体来说,你学到了:
- 如何加载和总结癌症生存数据集,并利用结果提出数据准备和模型配置建议。
- 如何探索简单MLP模型在数据集上的学习动态。
- 如何开发模型性能的稳健估计,调整模型性能并对新数据进行预测。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。

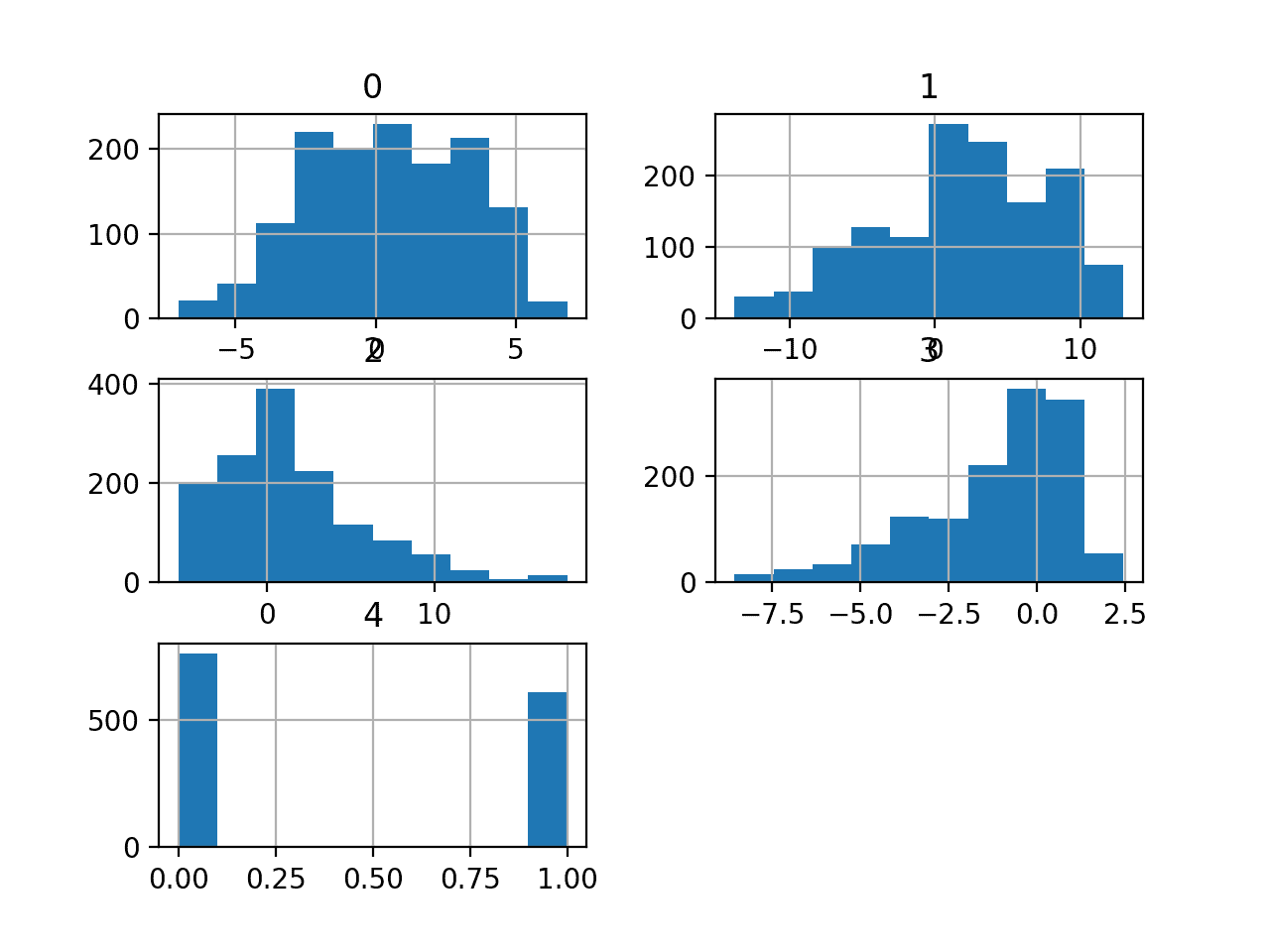
Jason您好。我对这句话感到困惑:“任何准确率低于73.5%的模型在这个数据集上都没有技能”。在ROC AUC文章中,您说对于不平衡数据集,准确率可能过于乐观。
对于这个模型(Dense(10)),您的准确率为76.5%,但F1分数=0 – 这是否意味着模型没有技能?
我之所以问这个问题,是因为当我应用 SMOTE 时,准确率降至71.6%,但F1分数提高到0.57。现在我感到困惑——模型现在有技能吗?哪个参数更重要?
更新:200个周期后F1不总是0.0。有时是0.127。
更新:我绘制了 F1 图表,并注意到它取决于正则化器。
如果 L2 >= 0.05,F1 会大幅波动。它在大约 50-70 个周期达到 ~0.2 的最大值然后下降。
如果 L2 < 0.05,F1 会稳步增长,在大约 250 个周期达到 ~0.5 的最大值。
如果 L2 < 0.003,F1 会快速增长,在大约 50 个周期达到 ~0.5 的最大值,但随后会发生过拟合。
因此 – 在 CV 分割 70/30(使用我的自定义 F1 回调)的情况下,不使用 SMOTE 的最佳结果是:
2 层 Dense(18) L2 = 0.008
准确率 = 79.35%
ROC AUC = 0.744
Recall AUC = 0.514
F1 分数 = 0.558
是的,F1 对这个数据集来说是更好的指标。
关于 F1 和准确率的这个问题:我们最好查看混淆矩阵,看看最终有多少 FP 或 FN……而且,可以说在像这样的医疗领域场景中,最应该避免的成本是避免 FN : )
谢谢 Jason。训练这个数据集非常复杂——我不得不阅读很多文章并进行了大量实验才获得一些结果。
现在我对如何解释它们感到困惑。
我将数据分成 70/30,假设我在 CV (X_test, y_test) 上获得了
准确率=75% F1=0.489。
然后我在整个数据集 (X,y) 上运行预测,结果更好:准确率=78.4% F1=0.535。
但对于不同的正则化器(L2 = 0.007),情况却相反。
准确率=80.39% F1=0.583 在 CV 数据集 (X_test, y_test) 上
准确率=77.43% F1=0.507 在整个数据集 (X,y) 上
整个数据集上的数字应该优先考虑吗?
这个数据集上达到的最好分数是多少?
我建议选择一个指标,以及一个稳健的测试框架,例如重复分层 k 折交叉验证。
先生,如何解决以下错误?我已经安装了 Keras。
No module named ‘keras.cross_validation’
我认为您的代码有误。
我的准确率是0。能告诉我原因吗?
你好 Diviya……你可能正在处理一个回归问题,并且实现了零预测误差。
或者,你可能正在处理分类问题并实现 100% 的准确率。
这很不寻常,原因有很多,包括:
你不小心在训练集上评估了模型性能。
你的保留数据集(训练集或验证集)太小或不具代表性。
你的代码中引入了一个错误,它正在做一些与你预期不同的事情。
你的预测问题很容易或微不足道,可能不需要机器学习。
最常见的原因是你的保留数据集太小或不代表更广泛的问题。
可以通过以下方法解决:
使用 k 折交叉验证来估计模型性能,而不是训练/测试拆分。
收集更多数据。
使用不同的数据拆分进行训练和测试,例如 50/50。
文本中提到了添加 dropout,但我在代码中没有看到。
Jason,我虽然发现您的文章比较晚,但还是饶有兴趣地读了,因为它反映了我30多年前的一个研究项目。我一直在尝试让您的源代码在不同于 Haberman 数据集的数据上运行。Haberman 数据实际上有一个很大的缺陷,手术操作日期通常对生存率的相关性很小。我想知道如何修改 Python 源代码来检查,比如,多于 n.3 个变量。
我的代码出现错误,因为“model.predict_classes()”自2021年起已被弃用,这显然是在您撰写本文之后。
我这样重写了它,似乎有效
from sklearn.metrics import accuracy_score
yhat = np.argmax(model.predict(X_test), axis=-1)
# ‘yhat’是‘预测’(我希望如此)
# 评估预测
score = accuracy_score(y_test, yhat)
print(‘\nAccuracy: %.3f’ % score)
我是一名医生,不是专业的程序员,所以请原谅。
你好 Daniel……感谢您的反馈!继续加油!
以下位置是开始构建机器学习知识的绝佳起点
https://machinelearning.org.cn/start-here/
嗨 James,
在“神经网络学习动态”章节中,我的准确率只有0.73。由于我使用的是不同版本的TF,我不知道我的代码是否发生了任何变化,从而影响了准确率。为了使其正常工作,我不得不调整了测试预测,将其设置为“yhat = np.argmax(model.predict(X_test), axis=1)”。我不知道这是否会影响准确率。我一直在阅读TF文档,但没有找到任何线索。
你好Alcides…你可能想在Google Colab中尝试你的代码,以确定是否存在任何版本差异。
嗨 James,
在Colab中,我的Tensorflow版本是2.12,而在我的机器上是2.13.0-rc。
运行完全相同的代码,我的准确率结果是一样的。也许是我自己做错了什么。