机器学习中的监督学习可以用函数逼近来描述。
给定一个由输入和输出组成的数据集,我们假设存在一个未知的底层函数,它在目标域中一致地将输入映射到输出,并由此生成了数据集。然后,我们使用监督学习算法来逼近这个函数。
神经网络是监督机器学习算法的一个例子,它或许在函数逼近的背景下最容易理解。这可以通过神经网络逼近简单一维函数的例子来演示,这有助于培养对模型正在学习什么的直觉。
在本教程中,您将了解神经网络作为函数逼近算法的直觉。
完成本教程后,您将了解:
- 在数据上训练神经网络可以逼近从输入到输出的未知底层映射函数。
- 一维输入和输出数据集为发展函数逼近的直觉提供了有用的基础。
- 如何开发和评估一个用于函数逼近的小型神经网络。
通过我的新书《使用Python进行深度学习》来启动您的项目,其中包括分步教程和所有示例的Python源代码文件。
让我们开始吧。

神经网络是函数近似算法
图片来自daveynin,保留部分权利。
教程概述
本教程分为三个部分;它们是:
- 什么是函数逼近
- 简单函数的定义
- 逼近一个简单函数
什么是函数逼近
函数逼近是一种利用领域中的历史或可用观测数据来估计未知底层函数的技术。
人工神经网络学习逼近一个函数。
在监督学习中,数据集由输入和输出组成,监督学习算法学习如何将输入的例子最好地映射到输出的例子。
我们可以将这种映射视为受一个数学函数(称为映射函数)控制,监督学习算法试图最好地逼近这个函数。
神经网络是监督学习算法的一个例子,它试图逼近数据所代表的函数。这是通过计算预测输出和预期输出之间的误差,并在训练过程中最小化此误差来实现的。
最好将前馈网络视为旨在实现统计泛化的函数逼近机器,偶尔从我们对大脑的了解中获取一些见解,而不是作为大脑功能的模型。
— 第169页,《深度学习》,2016年。
我们说“逼近”,是因为尽管我们怀疑存在这样的映射函数,但我们对其一无所知。
将输入映射到输出的真实函数是未知的,通常被称为目标函数。它是学习过程的目标,是我们试图仅使用可用数据来逼近的函数。如果我们知道目标函数,我们就不需要逼近它,即我们不需要监督机器学习算法。因此,函数逼近只有在底层目标映射函数未知时才是一个有用的工具。
我们所拥有的只是来自领域中包含输入和输出示例的观测数据。这暗示了数据的大小和质量;例如:
- 我们拥有的例子越多,我们就越有可能弄清楚映射函数。
- 观测数据中的噪声越少,我们对映射函数所做的逼近就越清晰。
那么,我们为什么喜欢使用神经网络进行函数逼近呢?
原因在于它们是通用逼近器。理论上,它们可以用来逼近任何函数。
...通用逼近定理指出,一个带有线性输出层和至少一个具有任何“挤压”激活函数(如逻辑S形激活函数)的隐藏层的前馈网络,可以以任意所需的非零误差量逼近从一个有限维空间到另一个有限维空间的任何[...]函数,前提是网络有足够的隐藏单元
— 第198页,《深度学习》,2016年。
回归预测建模涉及根据输入预测一个数值。分类预测建模涉及根据输入预测一个类别标签。
这两种预测建模问题都可以看作是函数逼近的例子。
为了使其具体化,我们可以回顾一个实例。
在下一节中,让我们定义一个可以稍后逼近的简单函数。
简单函数的定义
我们可以定义一个只有一个数值输入变量和一个数值输出变量的简单函数,并以此作为理解神经网络进行函数逼近的基础。
我们可以将一个数字域定义为我们的输入,例如从-50到50的浮点值。
然后,我们可以选择一个数学运算来应用于输入以获取输出值。所选择的数学运算将是映射函数,由于我们选择它,我们将知道它是什么。实际上,情况并非如此,这也是为什么我们会使用像神经网络这样的监督学习算法来学习或发现映射函数的原因。
在这种情况下,我们将使用输入的平方作为映射函数,定义为:
- y = x^2
其中 y 是输出变量,x 是输入变量。
我们可以通过列举输入变量范围内的值,并计算每个输入的输出值,然后绘制结果来对这个映射函数有一个直观的理解。
下面的例子在Python中实现了这一点。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# 创建一个具有给定映射函数的一元数据集的例子 from matplotlib import pyplot # 定义输入数据 x = [i for i in range(-50,51)] # 定义输出数据 y = [i**2.0 for i in x] # 绘制输入与输出的关系 pyplot.scatter(x,y) pyplot.title('输入 (x) 与输出 (y)') pyplot.xlabel('输入变量 (x)') pyplot.ylabel('输出变量 (y)') pyplot.show() |
运行示例首先会创建整个输入域中整数值的列表。
然后使用映射函数计算输出值,接着创建一个图表,x轴为输入值,y轴为输出值。
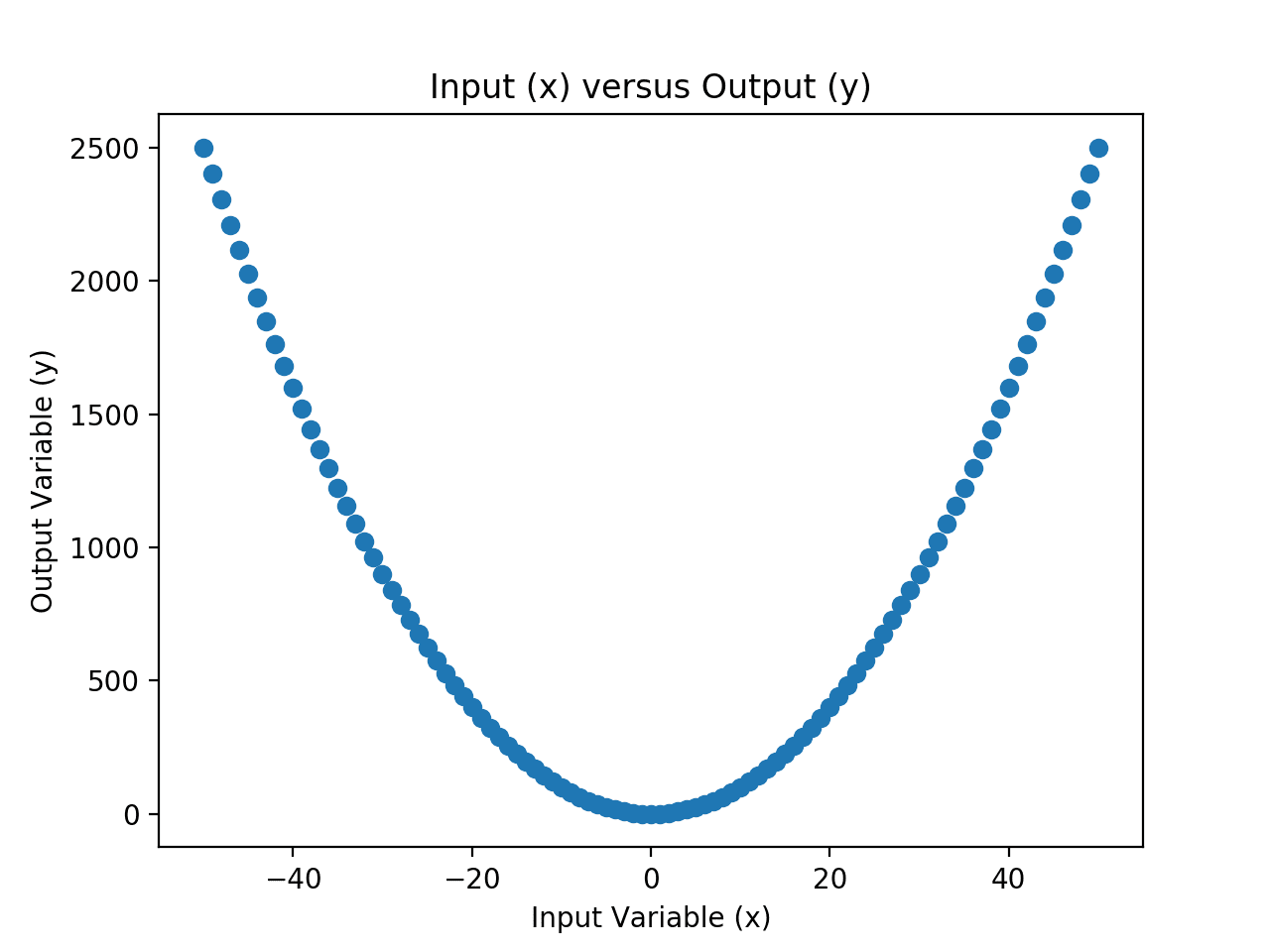
所选映射函数的输入和输出值散点图
输入和输出变量代表我们的数据集。
接下来,我们可以假装忘记我们知道映射函数是什么,然后使用神经网络重新学习或重新发现映射函数。
逼近一个简单函数
我们可以在输入和输出的例子上拟合一个神经网络模型,看看模型是否能学习到映射函数。
这是一个非常简单的映射函数,因此我们预计一个小型神经网络可以快速学习它。
我们将使用 Keras 深度学习库定义网络,并使用 scikit-learn 库中的一些数据准备工具。
首先,让我们定义数据集。
|
1 2 3 4 5 |
... # 定义数据集 x = asarray([i for i in range(-50,51)]) y = asarray([i**2.0 for i in x]) print(x.min(), x.max(), y.min(), y.max()) |
接下来,我们需要重塑数据,使输入和输出变量成为列,每行一个观测值,正如使用监督学习模型时所期望的那样。
|
1 2 3 4 |
... # 将数组重塑为行和列 x = x.reshape((len(x), 1)) y = y.reshape((len(y), 1)) |
接下来,我们需要对输入和输出进行缩放。
输入范围在-50到50之间,而输出范围在-50^2 (2500)到0^2 (0)之间。大的输入和输出值可能使神经网络训练不稳定,因此,最好先缩放数据。
我们可以使用MinMaxScaler分别将输入值和输出值归一化到0到1的范围内。
|
1 2 3 4 5 6 7 |
... # 分别缩放输入和输出变量 scale_x = MinMaxScaler() x = scale_x.fit_transform(x) scale_y = MinMaxScaler() y = scale_y.fit_transform(y) print(x.min(), x.max(), y.min(), y.max()) |
我们现在可以定义一个神经网络模型。
经过一些尝试和错误,我选择了一个带有两个隐藏层,每个层有10个节点的模型。或许可以尝试其他配置,看看能否做得更好。
|
1 2 3 4 5 6 |
... # 设计神经网络模型 model = Sequential() model.add(Dense(10, input_dim=1, activation='relu', kernel_initializer='he_uniform')) model.add(Dense(10, activation='relu', kernel_initializer='he_uniform')) model.add(Dense(1)) |
我们将使用均方损失拟合模型,并使用高效的 Adam 版随机梯度下降来优化模型。
这意味着模型将尝试在逼近映射函数时,最小化预测值和预期输出值(y)之间的均方误差。
|
1 2 3 |
... # 定义损失函数和优化算法 model.compile(loss='mse', optimizer='adam') |
我们没有很多数据(例如大约100行),所以我们将模型拟合500个 epoch,并使用10的小批量大小。
同样,这些值是在经过一些尝试和错误后找到的;尝试不同的值,看看您是否能做得更好。
|
1 2 3 |
... # 在训练数据集上拟合模型 model.fit(x, y, epochs=500, batch_size=10, verbose=0) |
一旦拟合,我们就可以评估模型。
我们将对数据集中的每个示例进行预测并计算误差。一个完美的逼近将是0.0。由于观测中的噪声、不完整的数据以及未知底层映射函数的复杂性,这通常是不可能的。
在这种情况下,这是可能的,因为我们拥有所有观测数据,数据中没有噪声,并且底层函数不复杂。
首先,我们可以进行预测。
|
1 2 3 |
... # 对输入数据进行预测 yhat = model.predict(x) |
然后我们必须反转我们执行的缩放。
这是为了使误差以目标变量的原始单位报告。
|
1 2 3 4 5 |
... # 反向转换 x_plot = scale_x.inverse_transform(x) y_plot = scale_y.inverse_transform(y) yhat_plot = scale_y.inverse_transform(yhat) |
然后我们可以计算并报告目标变量原始单位中的预测误差。
|
1 2 3 |
... # 报告模型误差 print('MSE: %.3f' % mean_squared_error(y_plot, yhat_plot)) |
最后,我们可以创建一个散点图,比较输入到输出的真实映射与输入到预测输出的映射,并从空间上看看映射函数的逼近情况。
这有助于培养对神经网络正在学习什么的直觉。
|
1 2 3 4 5 6 7 8 |
... # 绘制x与yhat的散点图 pyplot.scatter(x_plot,yhat_plot, label='预测值') pyplot.title('输入 (x) 与输出 (y)') pyplot.xlabel('输入变量 (x)') pyplot.ylabel('输出变量 (y)') pyplot.legend() pyplot.show() |
将这些结合起来,完整的示例列在下面。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 |
# 在x与x^2上拟合神经网络的例子 从 sklearn.预处理 导入 MinMaxScaler from sklearn.metrics import mean_squared_error from keras.models import Sequential from keras.layers import Dense from numpy import asarray from matplotlib import pyplot # 定义数据集 x = asarray([i for i in range(-50,51)]) y = asarray([i**2.0 for i in x]) print(x.min(), x.max(), y.min(), y.max()) # 将数组重塑为行和列 x = x.reshape((len(x), 1)) y = y.reshape((len(y), 1)) # 分别缩放输入和输出变量 scale_x = MinMaxScaler() x = scale_x.fit_transform(x) scale_y = MinMaxScaler() y = scale_y.fit_transform(y) print(x.min(), x.max(), y.min(), y.max()) # 设计神经网络模型 model = Sequential() model.add(Dense(10, input_dim=1, activation='relu', kernel_initializer='he_uniform')) model.add(Dense(10, activation='relu', kernel_initializer='he_uniform')) model.add(Dense(1)) # 定义损失函数和优化算法 model.compile(loss='mse', optimizer='adam') # 在训练数据集上拟合模型 model.fit(x, y, epochs=500, batch_size=10, verbose=0) # 对输入数据进行预测 yhat = model.predict(x) # 反向转换 x_plot = scale_x.inverse_transform(x) y_plot = scale_y.inverse_transform(y) yhat_plot = scale_y.inverse_transform(yhat) # 报告模型误差 print('MSE: %.3f' % mean_squared_error(y_plot, yhat_plot)) # 绘制x与y的散点图 pyplot.scatter(x_plot,y_plot, label='实际值') # 绘制x与yhat的散点图 pyplot.scatter(x_plot,yhat_plot, label='预测值') pyplot.title('输入 (x) 与输出 (y)') pyplot.xlabel('输入变量 (x)') pyplot.ylabel('输出变量 (y)') pyplot.legend() pyplot.show() |
运行该示例首先报告输入和输出变量的值范围,然后报告缩放后相同变量的范围。这证实了缩放操作正如我们预期地执行。
然后对数据集进行模型拟合和评估。
注意:由于算法或评估过程的随机性,或数值精度的差异,您的结果可能会有所不同。请考虑运行示例几次并比较平均结果。
在这种情况下,我们可以看到均方误差大约是1300,以平方单位表示。如果计算平方根,这将给出原始单位中的均方根误差 (RMSE)。我们可以看到平均误差大约是36个单位,这还可以,但不是很好。
你得到了什么结果?你能做得更好吗?
在下面的评论中告诉我。
|
1 2 3 |
-50 50 0.0 2500.0 0.0 1.0 0.0 1.0 均方误差:1300.776 |
然后创建一个散点图,比较输入与实际输出,以及输入与预测输出。
这两个数据系列之间的差异是映射函数逼近的误差。我们可以看到逼近是合理的;它捕捉到了大致的形状。我们可以看到存在误差,尤其是在输入值接近0的地方。
这表明仍有很大的改进空间,例如使用不同的激活函数或不同的网络架构来更好地逼近映射函数。
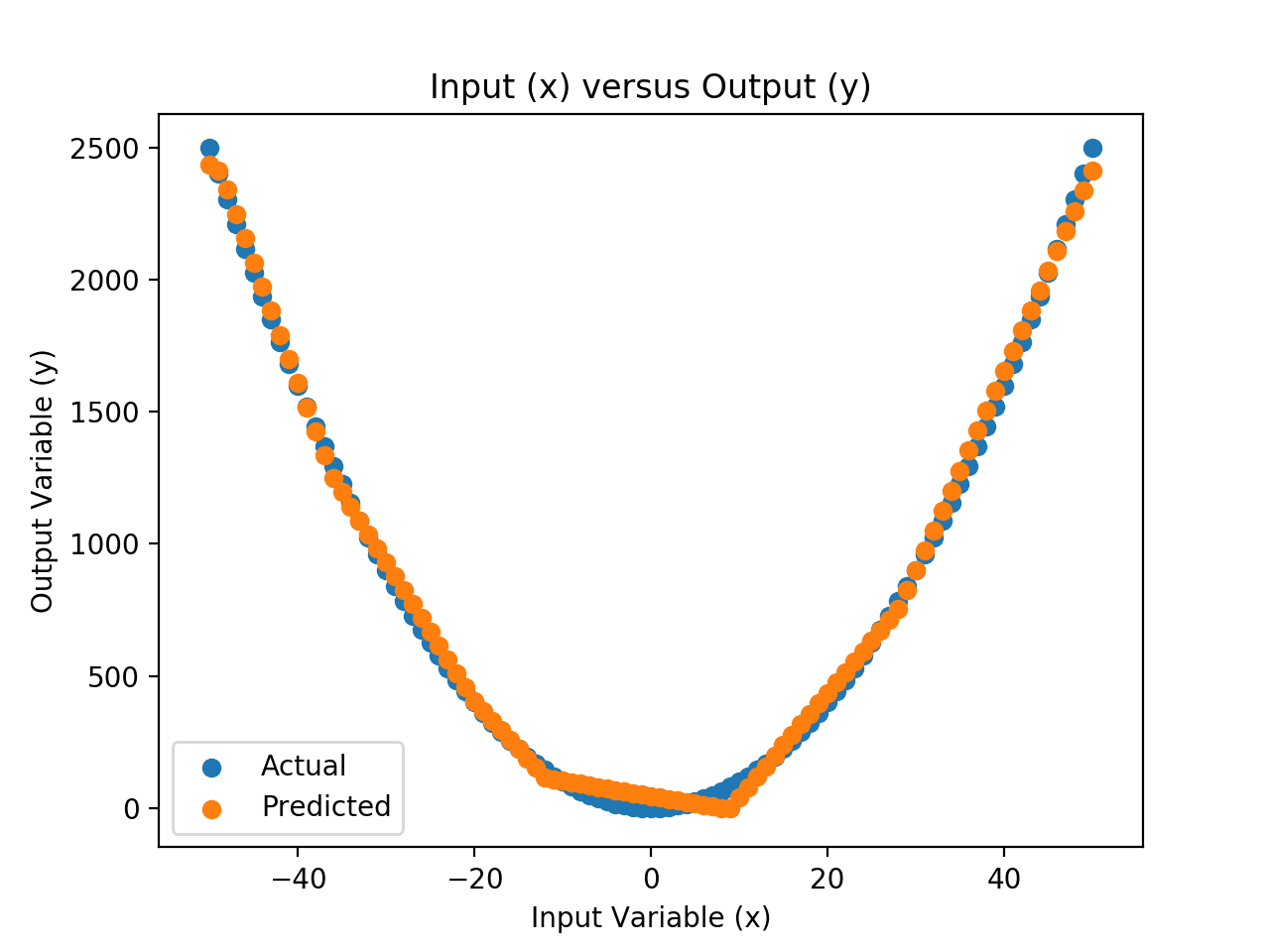
神经网络逼近的输入与实际值和预测值散点图
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
教程
书籍
- 深度学习, 2016.
文章
总结
在本教程中,您了解了神经网络作为函数逼近算法背后的直觉。
具体来说,你学到了:
- 在数据上训练神经网络可以逼近从输入到输出的未知底层映射函数。
- 一维输入和输出数据集为发展函数逼近的直觉提供了有用的基础。
- 如何开发和评估一个用于函数逼近的小型神经网络。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。






我建议生成随机值作为x_hat并预测y_hat。那样会更真实。你甚至可以为x获取随机值并计算y。
很好的建议,谢谢。
我还建议绘制残差 (y-y_hat) 在y轴上,以及您的输入变量在x轴上的散点图,以检查可辨别的模式。可辨别的模式意味着函数逼近需要改进。
好建议!始终检查您的残差。
函数逼近正是非参数回归所做的。有关它们的介绍,请参见此处 (https://cran.r-project.cn/web/packages/NNS/vignettes/NNSvignette_Clustering_and_Regression.html),有关它们在机器学习中(包括连续和离散分类问题)的扩展应用,请参见此处 (https://github.com/OVVO-Financial/NNS/tree/NNS-Beta-Version/examples#3-machine-learning)。
对于手头的问题,使用上述引用的NNS技术,MSE可以比所演示的NN表现得异常好。
在R中
> library(NNS)
> x = seq(-50,50,1); y = x^2
> y.hat = NNS.reg(x,y)$Fitted.xy$y.hat
> mean((y.hat – y)^2)
[1] 149.4403
很好,谢谢分享!
不客气!这篇文章很好地解释了函数逼近的重要性及其扩展。
谢谢。
然而,当每个n个权重只有一个非线性项时,传统的神经网络存在稀释问题。其中n是网络的宽度。这意味着对于像ReLU网络这样的网络,其“断点”比每个权重有一个非线性项(ReLU输出)时要少。这导致拟合效果不佳。
我想说(不是自高自大),神经网络研究人员应该回顾一下他们正在做的基本工作。
https://ai462qqq.blogspot.com/2019/11/artificial-neural-networks.html
https://discourse.numenta.org/t/and-there-they-stopped/7293
感谢分享。
喜欢这个关于我个人认为机器学习中最容易被忽视却最基本概念(即你在逼近一个函数)的简洁总结。鉴于你的能力,我很想看到你对“没有免费午餐”的看法。有没有可能写一篇关于清晰解释“没有免费午餐”的文章呢?🙂
谢谢。
好建议,我很了解它。重要的是要记住,您应该使用仔细而广泛的实验,而不是偏爱的算法来获得问题的最佳结果。
我认为,正如其他人提到的,用一些小的补充来增强这篇文章也会有所帮助(或者可以在后续文章中包含)。接下来,你可以在观测到的y值周围添加一个小的正态曲线误差,并展示会发生什么,解释为什么了解这一点很重要。另一件你可以做的事情是,砍掉两边的一些数据(最低和最高的x值),然后通过展示NN在训练样本耗尽后如何处理边缘来展示过拟合的效果。我在这里的期望是,如果你没有正确地进行过拟合训练,一旦NN达到边缘,它可能不知道该怎么办。如果使用测试集和训练集等进行正确训练,那么它可能会沿着边缘继续表现良好,并持续遵循y=x^2曲线。
很棒的拓展!
组织良好,演示出色。我喜欢阅读你的文章。
另一个建议是关于函数逼近和多值数据的文章。像x^2、sinx、cosx等函数就是其中之一。那会非常有趣。
谢谢。
好建议。
你好,Jason!我喜欢你的教程。我刚刚通过Tensorflow入门(https://colab.research.google.com/github/lmoroney/mlday-tokyo/blob/master/Lab1-Hello-ML-World.ipynb)回顾了同一个主题,使用了基本相同的问题,我被逼近的分段线性性质以及它对对称函数的不对称拟合所震惊。我尝试了不同数量的隐藏神经元、不同的激活函数和不同数量的 epoch,以更好地理解逼近的形状与这些变量的关系。你对这些问题有什么一般性的评论要补充吗?这样的思考对于这个教程来说可能是一个有用的补充,否则它似乎突然结束了。
尝试将隐藏层中的激活函数更改为 sigmoid。
好的……但我问这个问题之前已经这样做了。
谢谢。
“为什么”对于神经网络来说很难。
对于一个给定的模型,我们可以探索每个节点的计算并了解特定输出是如何产生的。如果我们将重点放在预测建模问题的模型技能上,这会非常耗时,并且收效甚微。我通常尽量避免为模型构建“为什么”的叙述。
https://machinelearning.org.cn/faq/single-faq/how-do-i-interpret-the-predictions-from-my-model
嗨,Jason,
很棒的函数逼近教程。我喜欢它!
在开始研究你使用GAN的其他教程(我对这种激进的“对抗网络方法”感到兴奋!)之前,我决定花一些时间研究这个教程。
在这里,我分享了我基于你的脚本变体的“实验”。感谢你提供如此简单且经过测试的代码。
我的评论
1º) 在我的观点中,函数或数据拟合方法在数学上与泰勒级数、最小二乘法(在Python中使用“scipy.optimize.curve_fit()”库解决)等相关。但在NN这种情况下,我们不必事先假设f(x)的类型……我们只是拟合数据!!所以在我看来,这是一种更先进的方法……
2º) 我在3个全连接层之外添加了其他层,例如BatchNormalization()、Dropout()。我还使用了l1_l2正则化器,但我得到的结果甚至比你基本的3个全连接层模型还要差!
3º) 我将全连接层中的10个单元数量更改为更高(50,100,...)和更低(5),但我没有得到任何关于你的最优模型的改进。
4º) 我决定不使用归一化数据(如MinMaxScaler()),所以我测试了原始(X,Y)数据……没有归一化……令人惊讶的是,代码仍然表现良好,并且稳定……我唯一的观察是它需要更多的(X,Y)样本!
5º) 除了二次函数和线性函数,我还测试了三次函数(X^3)……对于所有这些函数,它们都很好地拟合了整个数据集……但是有了更多的样本和更多的训练周期,我得到了更低的“均方根误差”,直到一个极限,大约是0.03。
6º) 我决定用相同的架构和模型测试三角函数(正弦),表现也非常好。
7º) 我决定用相同的架构和模型测试指数函数(a+e^bx+c),表现也非常好。
所以你的模型非常简单、稳健,并且在所有这些情况下都表现非常好……我所有的实验之后唯一的“发现”是,当我在数据集学习范围(Xmin-Xmax,Ymin-Ymax)之外测试值时,逼近或NN模型预测开始变差……越是超出范围,结果越差……所以它在范围内学习得很好……但它不能很好地泛化到该范围之外……除非你知道要应用后续方法(如“scipy.optimize.curve-fit()”)的函数类型……但在这种情况下,你需要假设预期函数的类型以及超出范围值的预测行为。
这就是我更喜欢神经网络“诚实”的原因……因为超出范围的值……你什么也无法肯定!……没有值可以测试!
正如我之前所说,我对我对GAN如何处理这些函数逼近学习与这种非常简单的NN方法感到兴奋!
此致,
JG
很酷,干得好!
根据函数的形式,神经网络可能外推得好,也可能不好。在这种情况下就不太好。函数可能有点太非线性,模型有点太简单。
将训练限制在有效输入空间的子集上,看看它是否能正确学习插值,这可能会很有趣。我期待它可以。这将表明它至少能在域内学习到可行的近似——这与你的外推实验有关。
你可以把你的实验写成教程,我立刻就会发布它们!
嗨,Jason,
更多关于我的实验的评论!
我回顾了几项NN函数逼近实验(多项式、三角函数和指数函数),针对不同空间子集数据集进行训练,我确认数据集训练范围之外的解随着距离训练范围越远而变得越差。无论如何,函数逼近在数据集训练归一化(应用于输入数据集处理)和更多训练样本的情况下效果更好!
三角函数(例如 F(X) = a*sine(f*X)+c 我解决了)的特殊情况是,如果我增加频率(“f”),函数逼近会失去 F(X) 的快速变化……唯一的解决方案是大幅增加数据集训练量(调整数量以捕捉 F(X) 的快速变化)。我欣赏某种“奈奎斯特-香农”采样率的必要性!
更糟糕的是,在这个三角函数的情况下,函数逼近在X训练范围之外根本不起作用。它似乎遵循一个比正确频率更低的模式。无论如何,它在训练范围之内是正常的。
问题
1º) 我有一个大问题。如果神经网络是X(假设一个唯一的特征或输入或X)和输出或F(X)=Y之间的映射。一旦模型学习完毕(我可以想象我们可以构建一个显式的权重,乘以输入(X)加上一些偏差,我们得到最终的“Y”或输出(F(X)))。
那么,在这种情况下,我们如何才能不显式地表达模型学习到的函数逼近,而不是继续将模型视为一个黑箱(无法显式映射)?
2º) 接着是F(X)映射的这个特殊情况……在X和F(X)之间,如果我们可以根据权重和偏差(这都是关于NN的)重构Y(输出)与X(唯一输入)的这种依赖关系,那么一个最终的常数(由权重乘积和加上输入X的偏差组成)如何能够重现一个更复杂的函数,例如F(X) = an*X^2 + a(n-1)*X^(n-1) + …b =0?
我可能对神经网络中的模型权重和偏差丢失了一些关键的东西,或者这只是北半球夏季炎热的问题:-))
是的,你可以手动使用前馈网络来执行映射,或者使用像Keras这样的框架。也许我没有理解你的第一个问题?
一个配置良好的神经网络理论上可以学习任何函数,无论是线性的还是非线性的。诀窍在于找到一个能够从示例中实际拟合它的配置和训练计划。
让我换一种方式来说。
如果权重(神经元之间的乘法系数)和偏差(模型层之间的加法)是常数(至少在模型学习过程结束时),那么我们就可以“理想地重构”模型输入(X)和输出(F(x))之间的数学关系……
这个最终的显式“方程”(至少对于我们有一个唯一输入X和唯一输出Y = F(X)的情况)可能如下所示:
Y = 常数(最终权重和偏差的乘法和加法) * X + 偏差(最终偏差结果)
所以我们最终得到了模型学习到的映射函数的显式设置……(这是一个重要的问题,可以解释或理解学习模型的T结果,而这通常是无法做到的)……这可能吗?还是我错了!
按照这种方法(我的第二个衍生问题),因此我不明白这个最终方程如何能重现例如一个更复杂的多项式,如F(X) = a* x^4+ b *X^3 + c*X^2 + d*X + sin(X) + ..。它只是 = 常数 +X + 常数 !!
我想我可能错过了任何模型学习到的最终权重和偏差的关键之处……:-(
这有可能,有些人也确实这么做,但它会很庞大,充满了矩阵乘法,比如一团糟,难以阅读。
函数的近似值看起来会非常不同,令人无法辨认。这让一些从业者感到抓狂并放弃。
:-)) 谢谢Jason!
不客气。
嗨,Jason,
首先,非常感谢你辛勤创作的优秀内容。
我有一个问题。我创建了一个简单的反V形数据集,并添加了能够拟合这些数据的最少层数和节点数,如下所示。我一半的随机训练尝试都导致了不拟合的线条(损失值非常高,可能达到了局部最小值?),另一半则完美拟合(我想它找到了全局最小值)。
然而,当我在你的例子中增加每层的层数和节点数时,完美拟合的几率约为95%。剩下的5%中,损失值仍然非常高。
我的问题是,为什么增加层数和节点数会增加拟合的几率?
import numpy as np
import matplotlib.pyplot as plt
from keras import models
from keras import layers
from keras import optimizers
X_1 = np.linspace(-5,0,25)
y_1 = 5 + X_1 + 0.2*np.random.normal(0,1,size=25)
X_2 = np.linspace(0,5,25)
y_2 = 5 – X_2 + 0.2*np.random.normal(0,1,size=25)
X=np.concatenate((X_1,X_2))
y=np.concatenate((y_1,y_2))
fig, ax = plt.subplots()
ax.set_title(“线性回归”)
ax.scatter(X, y, label=”训练数据”,s=1)
ax.grid()
model = models.Sequential()
model.add(layers.Dense(2,activation = ‘relu’))
model.add(layers.Dense(1,activation=”linear”))
model.compile(loss=’mean_squared_error’, optimizer=optimizers.Adam(lr=0.1))
history = model.fit(X,y, epochs=500, verbose=1)
y_hat = model.predict(X)
ax.plot(X,y_hat,’r’)
fig.tight_layout()
好问题,改变模型的架构将改变可以拟合的函数类型。
在使用神经网络时,我们面临着一项艰巨的任务:找到一个好的架构(函数集)和一个好的优化处理(学习配置)。
你好Jason,文章很棒。我是一个Python新手。抱歉问一个(对你来说可能很简单)问题。我尝试重现示例,但我失败了。我正在使用Spyder(anaconda 1.10)。出现了一个关于keras的错误。
File “C:\Users\Usuario\Documents\Data Science\1 Python_Examples\fitting_NeuralNet_on dataset.py”, line 10, in
来自 keras.models import Sequential
ModuleNotFoundError: 没有名为 'keras' 的模块
我按照以下方式安装了keras:python -m pip install –user keras。甚至尝试了更新keras,但仍然无效。你能帮忙解决这个问题吗?
祝好,
埃德温
也许可以尝试将代码复制到一个新文件中,保存文件并从命令行运行Python脚本。
https://machinelearning.org.cn/faq/single-faq/how-do-i-run-a-script-from-the-command-line
此外,请根据本教程中的建议,确认Keras已安装并在命令行中可用。
https://machinelearning.org.cn/setup-python-environment-machine-learning-deep-learning-anaconda/
嗨,Jason,
非常感谢。确认keras的教程确实奏效了!我非常感谢你所做的一切。
还有一件事想请教,我尝试在Pycharm中运行你的教程,但我认为发生了一些与Anaconda中类似的问题。这次它没有识别出大部分函数(pyplot、numpy等)。下面是一个例子:
ModuleNotFoundError: No module named ‘matplotlib’
你有什么建议?
祝好,
埃德温
谢谢!
看起来你还没有安装matplotlib库。
另外,我建议不要使用IDE,这里有更多解释。
https://machinelearning.org.cn/faq/single-faq/why-dont-use-or-recommend-notebooks
非常好,但是我不使用库。
那么你可能会喜欢这篇文章:https://machinelearning.org.cn/implement-backpropagation-algorithm-scratch-python/
完全从零开始构建一个神经网络!
有没有更新的、针对 Keras 的多变量输入输出版本的示例?我有一个问题,有 5 个特征,输出 3 个数字,这很可能是一些标准差公式。也许是移动平均。我有数百万个样本用于监督学习,这似乎是解码它的好方法。
对于多变量,简单的更改是更改input_dim和模型中最终Dense(n)括号中的数字。它们分别对应输入和输出维度。然而,由于多变量本身更复杂,您可能需要更多的隐藏层才能产生好的结果。
在哪里可以找到第10课的神经实验室程序函数逼近。谢谢你!
Nick
你好Nick…请澄清你指的是什么,以便我们更好地帮助你。
你好,谢谢你的快速回复。那是通过神经网络逼近实验数据y=f(x)的依赖关系,参考https://www.youtube.com/watch?v=kze0QxYzo5w
亲爱的詹姆斯!
抱歉打扰,我已经解决了问题。