朴素贝叶斯算法是一种简单但功能强大的监督机器学习技术。其高斯变体在 OpenCV 库中实现。
在本教程中，您将学习如何应用 OpenCV 的普通贝叶斯算法，首先在自定义的二维数据集上，然后用于图像分割。
完成本教程后，您将了解：
- 将贝叶斯定理应用于机器学习的几个最重要点。
- 如何在 OpenCV 中将普通贝叶斯算法应用于自定义数据集。
- 如何在 OpenCV 中使用普通贝叶斯算法分割图像。
通过我的书《OpenCV 机器学习》启动您的项目。它提供了带有可用代码的自学教程。
让我们开始吧。
使用 OpenCV 进行图像分割的正态贝叶斯分类器
照片由 Fabian Irsara 拍摄，保留部分权利。
教程概述
本教程分为三个部分；它们是：
- 贝叶斯定理在机器学习中的应用回顾
- 探索 OpenCV 中的贝叶斯分类
- 使用普通贝叶斯分类器进行图像分割
贝叶斯定理在机器学习中的应用回顾
Jason Brownlee 的本教程深入解释了机器学习的贝叶斯定理，所以我们先从回顾他教程中的一些最重要点开始
贝叶斯定理在机器学习中很有用，因为它提供了一个统计模型来阐述数据和假设之间的关系。
- 贝叶斯定理表示为 $P(h | D) = P(D | h) * P(h) / P(D)$，它指出给定假设为真的概率（表示为 $P(h | D)$，称为假设的后验概率）可以通过以下方式计算：
-
- 在给定假设的情况下观察数据的概率（表示为 $P(D | h)$，称为似然）。
- 假设为真的概率，与数据无关（表示为 $P(h)$，称为假设的先验概率）。
- 独立于假设观察数据的概率（表示为 $P(D)$，称为证据）。
- 贝叶斯定理假设构成输入数据 $D$ 的每个变量（或特征）都依赖于所有其他变量（或特征）。
- 在数据分类的背景下，贝叶斯定理可以应用于计算给定数据样本的类别标签的条件概率问题：$P(class | data) = P(data | class) * P(class) / P(data)$，其中类别标签现在取代了假设。证据 $P(data)$ 是一个常数，可以省略。
- 在上述要点概述的问题表述中，似然 $P(data | class)$ 的估计可能很困难，因为它要求数据样本的数量足够大，以包含每个类别的所有可能的变量（或特征）组合。这种情况很少出现，尤其是在具有许多变量的高维数据中。
- 上述公式可以简化为朴素贝叶斯，其中每个输入变量都被单独处理：$P(class | X_1, X_2, \dots, X_n) = P(X_1 | class) * P(X_2 | class) * \dots * P(X_n | class) * P(class)$
- 朴素贝叶斯估计将公式从依赖条件概率模型更改为独立条件概率模型，其中输入变量（或特征）现在被假定为独立的。这个假设在真实世界数据中很少成立，因此得名朴素。
探索 OpenCV 中的贝叶斯分类
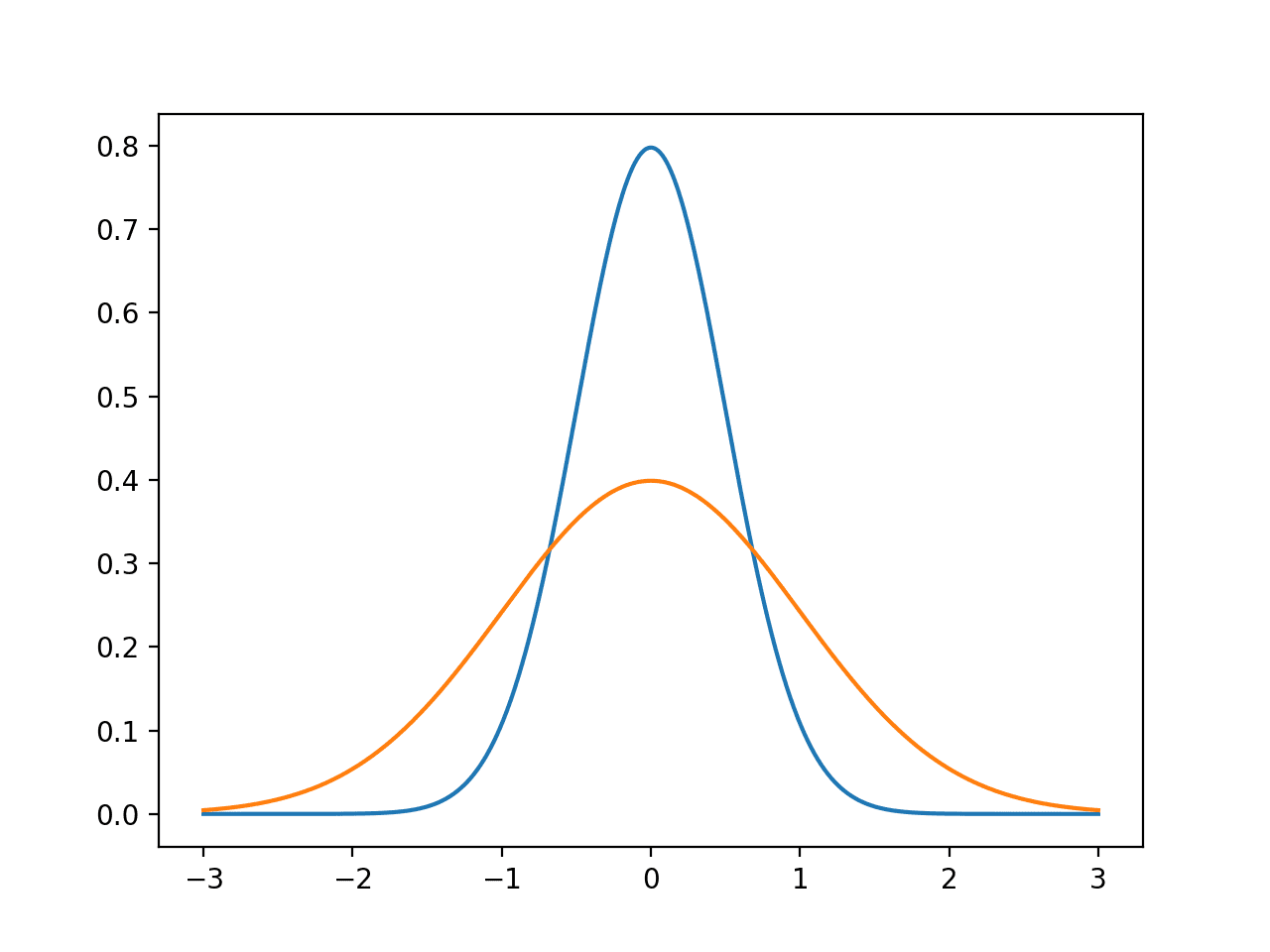
假设我们正在处理的输入数据是连续的。在这种情况下，可以使用连续概率分布（例如高斯（或正态）分布）对其进行建模，其中属于每个类的数据由其均值和标准差建模。
OpenCV 中实现的贝叶斯分类器是普通贝叶斯分类器（也常称为高斯朴素贝叶斯），它假设每个类的输入特征呈正态分布。
这个简单的分类模型假设每个类的特征向量都呈正态分布（尽管不一定独立分布）。
– OpenCV，机器学习概述，2023。
要了解如何在 OpenCV 中使用普通贝叶斯分类器，我们首先在简单的二维数据集上进行测试，就像我们在之前的教程中所做的那样。
想开始学习 OpenCV 机器学习吗？
立即参加我的免费电子邮件速成课程（附示例代码）。
点击注册，同时获得该课程的免费PDF电子书版本。
为此，让我们生成一个包含 100 个数据点（由 n_samples 指定）的数据集，这些数据点平均分为 2 个高斯簇（由 centers 标识），标准差设置为 1.5（由 cluster_std 指定）。我们还定义 random_state 的值，以便能够重现结果
|
1 2 3 4 5 6 |
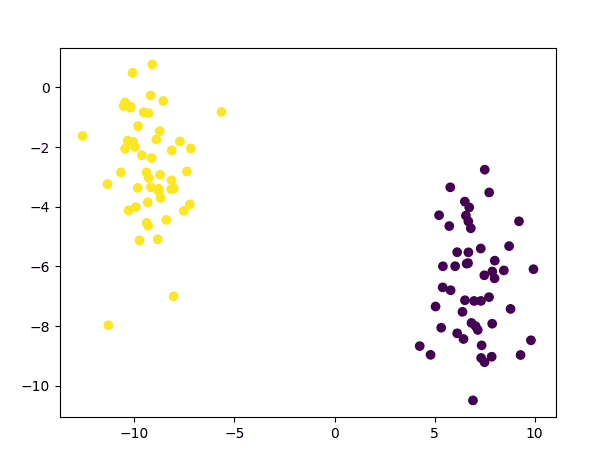
# 生成一个二维数据点及其真实标签的数据集 x, y_true = make_blobs(n_samples=100, centers=2, cluster_std=1.5, random_state=15) # 绘制数据集 scatter(x[:, 0], x[:, 1], c=y_true) show() |
上面的代码应该生成以下数据点图
由 2 个高斯簇组成的数据集散点图
然后我们将分割此数据集，将 80% 的数据分配给训练集，剩余 20% 分配给测试集
|
1 2 |
# 将数据拆分为训练集和测试集 x_train, x_test, y_train, y_test = ms.train_test_split(x, y_true, test_size=0.2, random_state=10) |
在此之后，我们将创建普通贝叶斯分类器，并在将数据集值类型转换为 32 位浮点数后，继续对其进行训练和测试
|
1 2 3 4 5 6 7 8 |
# 创建一个新的普通贝叶斯分类器 norm_bayes = ml.NormalBayesClassifier_create() # 在训练数据上训练分类器 norm_bayes.train(x_train.astype(float32), ml.ROW_SAMPLE, y_train) # 从训练好的分类器生成预测 ret, y_pred, y_probs = norm_bayes.predictProb(x_test.astype(float32)) |
通过使用 predictProb 方法，我们将获得每个输入向量的预测类别（每个向量存储在输入到普通贝叶斯分类器的数组的每一行中）和输出概率。
在上面的代码中，预测的类别存储在 y_pred 中，而 y_probs 是一个具有与类别一样多列（本例中为两列）的数组，其中包含每个输入向量属于所考虑的每个类别的概率值。分类器为每个输入向量返回的输出概率值总和为一是有道理的。然而，情况可能并非如此，因为分类器返回的概率值未通过证据 $P(data)$ 进行归一化，正如上一节所述，我们已将其从分母中删除。
相反，报告的是似然，它基本上是条件概率方程 p(C) p(M | C) 的分子。分母 p(M) 不需要计算。
– OpenCV 机器学习，2017。
尽管如此，无论值是否归一化，都可以通过识别具有最高概率值的类别来找到每个输入向量的类别预测。
目前的代码清单如下
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
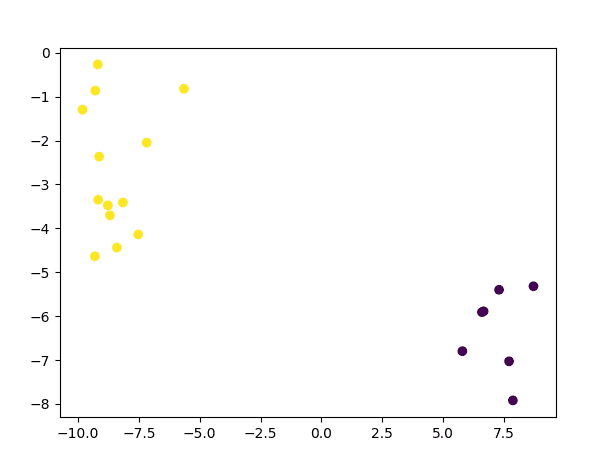
from sklearn.datasets import make_blobs from sklearn import model_selection as ms from numpy import float32 from matplotlib.pyplot import scatter, show from cv2 import ml # 生成一个二维数据点及其真实标签的数据集 x, y_true = make_blobs(n_samples=100, centers=2, cluster_std=1.5, random_state=15) # 绘制数据集 scatter(x[:, 0], x[:, 1], c=y_true) show() # 将数据拆分为训练集和测试集 x_train, x_test, y_train, y_test = ms.train_test_split(x, y_true, test_size=0.2, random_state=10) # 创建一个新的普通贝叶斯分类器 norm_bayes = ml.NormalBayesClassifier_create() # 在训练数据上训练分类器 norm_bayes.train(x_train.astype(float32), ml.ROW_SAMPLE, y_train) # 从训练好的分类器生成预测 ret, y_pred, y_probs = norm_bayes.predictProb(x_test.astype(float32)) # 绘制类别预测 scatter(x_test[:, 0], x_test[:, 1], c=y_pred) show() |
我们可以看到，在这个简单数据集上训练的普通贝叶斯分类器产生的类别预测是正确的
测试样本预测散点图
使用普通贝叶斯分类器进行图像分割
在众多应用中，贝叶斯分类器常用于皮肤分割，将图像中的皮肤像素与非皮肤像素分开。
我们可以修改上面的代码来分割图像中的皮肤像素。为此，我们将使用皮肤分割数据集，它包含 50,859 个皮肤样本和 194,198 个非皮肤样本，来训练普通贝叶斯分类器。该数据集以 BGR 顺序和其对应的类别标签呈现像素值。
加载数据集后，我们将把 BGR 像素值转换为 HSV（表示色相、饱和度和亮度），然后使用色相值来训练普通贝叶斯分类器。在图像分割任务中，色相通常比 RGB 更受青睐，因为它代表真实的颜色而没有修改，并且受光照变化的影响比 RGB 小。在 HSV 颜色模型中，色相值径向排列，范围在 0 到 360 度之间。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
from cv2 import ml, from numpy import loadtxt, float32 from matplotlib.colors import rgb_to_hsv # 从文本文件中加载数据 data = loadtxt("Data/Skin_NonSkin.txt", dtype=int) # 从加载的数据中选择 BGR 值 BGR = data[:, :3] # 通过交换数组列转换为 RGB RGB = BGR.copy() RGB[:, [2, 0]] = RGB[:, [0, 2]] # 将 RGB 值转换为 HSV HSV = rgb_to_hsv(face_RGB.reshape(face_RGB.shape[0], -1, 3) / 255) HSV = HSV.reshape(RGB.shape[0], 3) # 只选择色相值 hue = HSV[:, 0] * 360 # 从加载的数据中选择标签 labels = data[:, -1] # 创建一个新的普通贝叶斯分类器 norm_bayes = ml.NormalBayesClassifier_create() # 在色相值上训练分类器 norm_bayes.train(hue.astype(float32), ml.ROW_SAMPLE, labels) |
注 1：OpenCV 库提供了 cvtColor 方法用于在颜色空间之间进行转换，如本教程所示，但 cvtColor 方法需要原始形状的源图像作为输入。另一方面，Matplotlib 中的 rgb_to_hsv 方法接受 (..., 3) 形式的 NumPy 数组作为输入，其中数组值应归一化到 0 到 1 的范围。我们在这里使用后者，因为我们的训练数据由单个像素组成，它们不以常见的三通道图像形式组织。
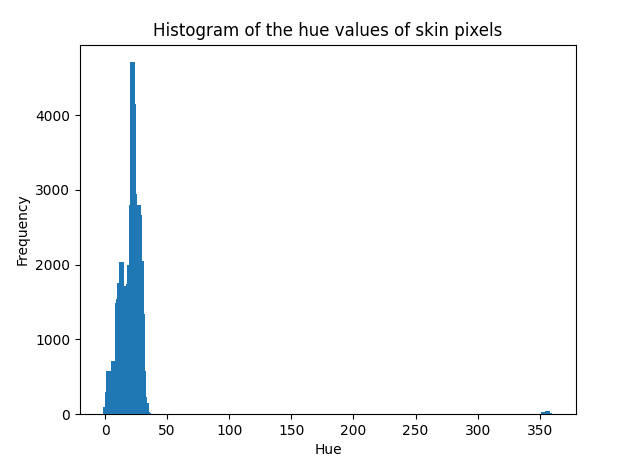
注 2：普通贝叶斯分类器假设要建模的数据服从高斯分布。虽然这不是一个严格的要求，但如果数据分布方式不同，分类器的性能可能会下降。我们可以通过绘制数据的直方图来检查我们正在处理的数据的分布。如果我们以皮肤像素的色相值为例，我们会发现高斯曲线可以描述它们的分布
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
from numpy import histogram from matplotlib.pyplot import bar, title, xlabel, ylabel, show # 选择皮肤标记的色相值 skin = x[labels == 1] # 计算它们的直方图 hist, bin_edges = histogram(skin, range=[0, 360], bins=360) # 显示计算出的直方图 bar(bin_edges[:-1], hist, width=4) xlabel('色相') ylabel('频率') title('皮肤像素色相值的直方图') show() |
检查数据分布
一旦普通贝叶斯分类器训练完成，我们就可以在一张图像上进行测试（我们以这张示例图像为例进行测试）
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
from cv2 import imread from matplotlib.pyplot import show, imshow # 加载测试图像 face_img = imread("Images/face.jpg") # 将图像重塑为三列数组 face_BGR = face_img.reshape(-1, 3) # 通过交换数组列转换为 RGB face_RGB = face_BGR.copy() face_RGB[:, [2, 0]] = face_RGB[:, [0, 2]] # 从 RGB 转换为 HSV face_HSV = rgb_to_hsv(face_RGB.reshape(face_RGB.shape[0], -1, 3) / 255) face_HSV = face_HSV.reshape(face_RGB.shape[0], 3) # 只选择色相值 face_hue = face_HSV[:, 0] * 360 # 显示色相图像 imshow(face_hue.reshape(face_img.shape[0], face_img.shape[1])) show() # 从训练好的分类器生成预测 ret, labels_pred, output_probs = norm_bayes.predictProb(face_hue.astype(float32)) # 将数组重塑为输入图像大小，并选择皮肤标记的像素 skin_mask = labels_pred.reshape(face_img.shape[0], face_img.shape[1], 1) == 1 # 显示分割后的图像 imshow(skin_mask, cmap='gray') show() |
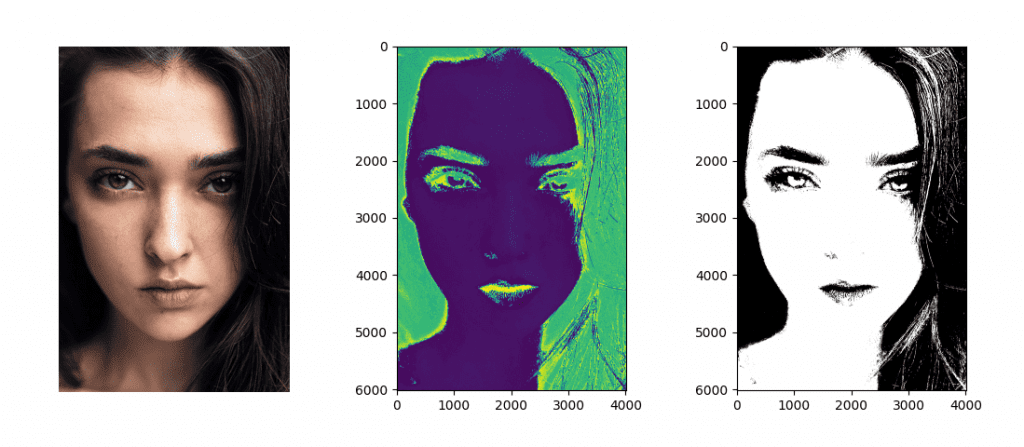
分割后的结果掩码显示了被标记为皮肤的像素（类别标签等于 1）。
通过定性分析结果，我们可以看到大部分皮肤像素都被正确标记。我们还可以看到一些发丝（因此是非皮肤像素）被错误地标记为皮肤。如果我们查看它们的色相值，我们可能会注意到它们与皮肤区域的色相值非常相似，因此导致了错误标记。此外，我们还可以注意到使用色相值的有效性，在原始 RGB 图像中显得明亮或阴影的脸部区域，色相值保持相对恒定
原始图像（左）；色相值（中）；分割后的皮肤像素（右）
您还能想到用普通贝叶斯分类器进行哪些测试吗？
进一步阅读
如果您想深入了解此主题，本节提供了更多资源。
书籍
- OpenCV 机器学习, 2017.
- 使用 Python 精通 OpenCV 4, 2019.
总结
在本教程中，您学习了如何应用 OpenCV 的普通贝叶斯算法，首先在自定义的二维数据集上，然后用于图像分割。
具体来说，你学到了：
- 将贝叶斯定理应用于机器学习的几个最重要点。
- 如何在 OpenCV 中将普通贝叶斯算法应用于自定义数据集。
- 如何在 OpenCV 中使用普通贝叶斯算法分割图像。
你有什么问题吗？
在下面的评论中提出您的问题，我将尽力回答。
开始使用 OpenCV 进行机器学习！
学习如何在图像处理项目中使用机器学习技术
...以高级方式使用 OpenCV，超越像素处理
在我的新电子书中探索如何实现
OpenCV 机器学习
它提供带有所有可用 Python 代码的自学教程，让您从新手成长为专家。它为您提供了
逻辑回归、随机森林、支持向量机、k 均值聚类、神经网络等等……所有这些都使用 OpenCV 中的机器学习模块
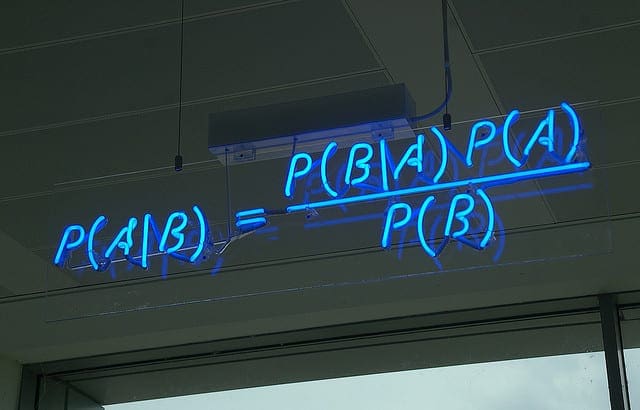
暂无评论。