分类算法学习如何将类别标签分配给示例,尽管它们的决策可能显得不透明。
理解分类算法所做决策的一种常用诊断工具是**决策面**。这是一个图表,显示了已拟合的机器学习算法如何预测输入特征空间上的粗网格。
决策面图是一种强大的工具,用于理解给定模型“_如何看待_”预测任务,以及它如何决定按类别标签划分输入特征空间。
在本教程中,您将学习如何绘制分类机器学习算法的决策面。
完成本教程后,您将了解:
- 决策面是一种诊断工具,用于理解分类算法如何划分特征空间。
- 如何使用清晰的类别标签为机器学习算法绘制决策面。
- 如何使用预测概率绘制和解释决策面。
通过我的新书《使用 Python 进行机器学习精通》**启动您的项目**,其中包括_分步教程_和所有示例的_Python 源代码_文件。
让我们开始吧。

在 Python 中绘制机器学习算法的决策面
图片来自 Tony Webster,保留部分权利。
教程概述
本教程分为三个部分;它们是:
- 决策面
- 数据集和模型
- 绘制决策面
决策面
分类机器学习算法学习将标签分配给输入示例。
考虑用于分类任务的数值输入特征,这些特征定义了一个连续的输入特征空间。
我们可以将每个输入特征视为定义特征空间上的一个轴或维度。两个输入特征将定义一个平面特征空间,点代表输入空间中的输入坐标。如果存在三个输入变量,则特征空间将是一个三维体积。
空间中的每个点都可以分配一个类别标签。在二维特征空间中,我们可以将平面上的每个点根据其分配的类别具有不同的颜色。
分类算法的目标是学习如何划分特征空间,以便将标签正确地分配给特征空间中的点,或者至少尽可能正确地分配。
这是对分类预测建模的有用几何理解。我们可以更进一步。
一旦分类机器学习算法划分了特征空间,我们就可以对特征空间中的每个点(在任意网格上)进行分类,以了解算法究竟是如何选择划分特征空间的。
这称为**决策面**或**决策边界**,它提供了一种诊断工具,用于理解分类预测建模任务中的模型。
尽管“_表面_”的概念暗示二维特征空间,但该方法可用于具有两个以上维度的特征空间,其中为每对输入特征创建一个表面。
现在我们熟悉了什么是决策面,接下来,让我们定义一个数据集和模型,稍后我们将探索其决策面。
数据集和模型
在本节中,我们将定义一个分类任务和预测模型来学习该任务。
合成分类数据集
我们可以使用 make_blobs() scikit-learn 函数来定义一个分类任务,该任务具有二维类别数值特征空间,并且每个点分配两个类别标签之一,例如二元分类任务。
|
1 2 3 |
... # 生成数据集 X, y = make_blobs(n_samples=1000, centers=2, n_features=2, random_state=1, cluster_std=3) |
定义后,我们可以创建特征空间的散点图,其中第一个特征定义 x 轴,第二个特征定义 y 轴,每个样本表示为特征空间中的一个点。
然后我们可以根据它们的类别标签(0 或 1)对散点图中的点进行着色。
|
1 2 3 4 5 6 7 8 9 |
... # 为每个类别的样本创建散点图 for class_value in range(2): # 获取具有此类别的样本的行索引 row_ix = where(y == class_value) # 创建这些样本的散点图 pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # 显示绘图 pyplot.show() |
综合起来,下面列出了定义和绘制合成分类数据集的完整示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# 生成二元分类数据集并绘制 from numpy import where from matplotlib import pyplot from sklearn.datasets import make_blobs # 生成数据集 X, y = make_blobs(n_samples=1000, centers=2, n_features=2, random_state=1, cluster_std=3) # 为每个类别的样本创建散点图 for class_value in range(2): # 获取具有此类别的样本的行索引 row_ix = where(y == class_value) # 创建这些样本的散点图 pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # 显示绘图 pyplot.show() |
运行示例会创建数据集,然后将数据集绘制成散点图,点按类别标签着色。
我们可以看到两个类别之间的清晰分离,我们可以想象机器学习模型如何画一条线来分离这两个类别,例如,可能是一条穿过两组中间的对角线。
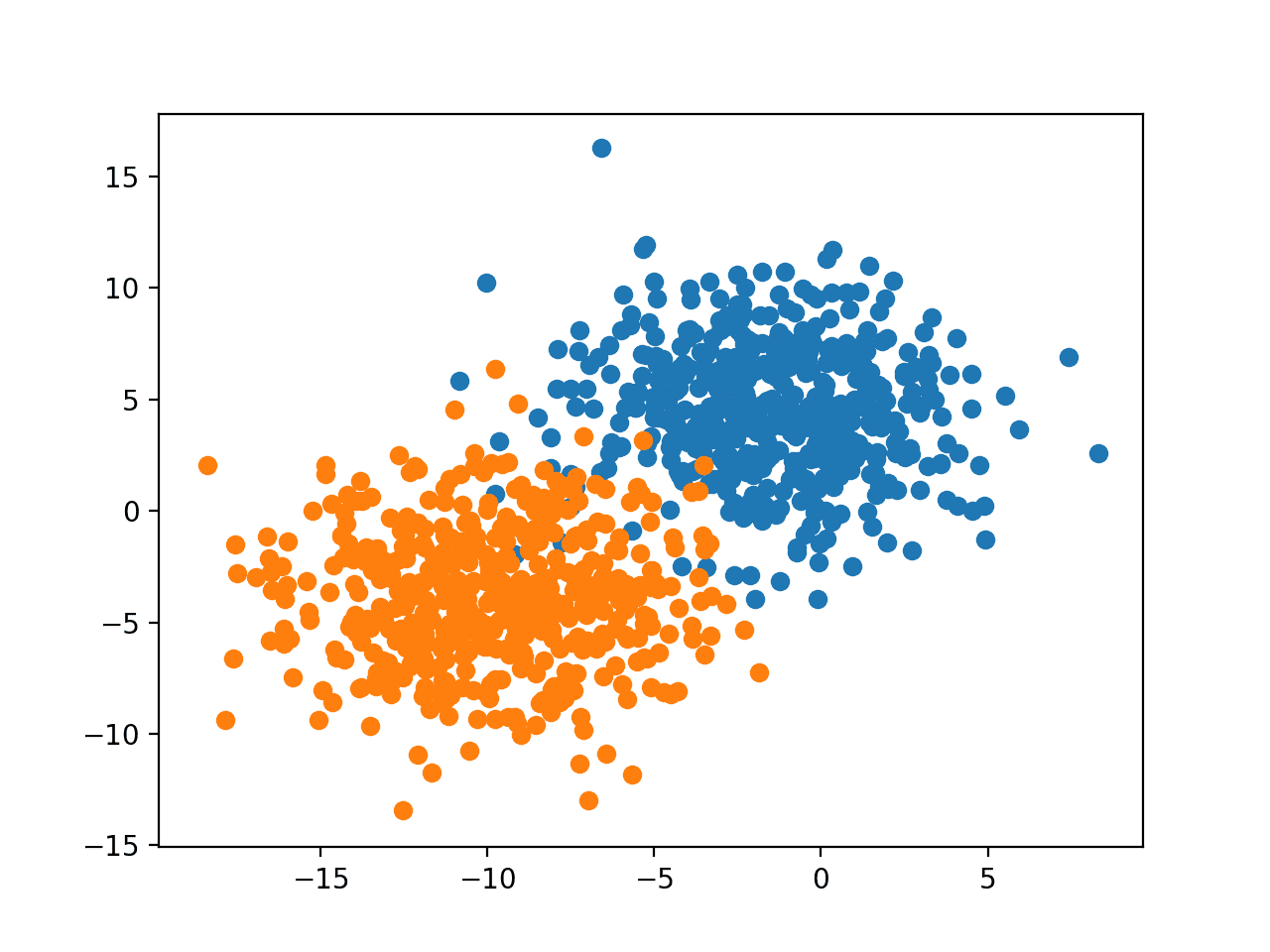
具有二维特征空间的二元分类数据集散点图
拟合分类预测模型
现在我们可以在我们的数据集上拟合一个模型。
在这种情况下,我们将拟合一个逻辑回归算法,因为我们可以预测清晰的类别标签和概率,两者都可以在我们的决策面中使用。
我们可以定义模型,然后在训练数据集上拟合它。
|
1 2 3 4 5 |
... # 定义模型 model = LogisticRegression() # 拟合模型 model.fit(X, y) |
定义后,我们可以使用该模型对训练数据集进行预测,以了解它学习如何划分训练数据集的特征空间并分配标签的效果如何。
|
1 2 3 |
... # 进行预测 yhat = model.predict(X) |
预测可以使用分类准确度进行评估。
|
1 2 3 4 |
... # 评估预测 acc = accuracy_score(y, yhat) print('Accuracy: %.3f' % acc) |
综合起来,下面列出了在合成二元分类数据集上拟合和评估模型的完整示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
# 在分类数据集上拟合和评估模型的示例 from sklearn.datasets import make_blobs from sklearn.linear_model import LogisticRegression from sklearn.metrics import accuracy_score # 生成数据集 X, y = make_blobs(n_samples=1000, centers=2, n_features=2, random_state=1, cluster_std=3) # 定义模型 model = LogisticRegression() # 拟合模型 model.fit(X, y) # 进行预测 yhat = model.predict(X) # 评估预测 acc = accuracy_score(y, yhat) print('Accuracy: %.3f' % acc) |
运行示例会拟合模型并对每个示例进行预测。
**注意**:考虑到算法或评估过程的随机性,或者数值精度差异,您的结果可能会有所不同。考虑多次运行示例并比较平均结果。
在这种情况下,我们可以看到模型的性能约为 97.2%。
|
1 |
准确率:0.972 |
现在我们有了一个数据集和模型,让我们探讨如何开发决策面。
绘制决策面
我们可以通过在训练数据集上拟合模型,然后使用该模型对输入域上的网格值进行预测来创建决策面。
一旦我们有了预测网格,我们就可以绘制值及其类别标签。
如果采用足够精细的网格,可以使用散点图。更好的方法是使用可以插值点之间颜色的等高线图。
可以使用 contourf() Matplotlib 函数。
这需要几个步骤。
首先,我们需要在特征空间中定义一个点网格。
为此,我们可以找到每个特征的最小值和最大值,并将网格扩展一步,以确保覆盖整个特征空间。
|
1 2 3 4 |
... # 定义域的边界 min1, max1 = X[:, 0].min()-1, X[:, 0].max()+1 min2, max2 = X[:, 1].min()-1, X[:, 1].max()+1 |
然后我们可以使用 arange() 函数以选定的分辨率在每个维度上创建均匀样本。在这种情况下,我们将使用 0.1 的分辨率。
|
1 2 3 4 |
... # 定义 x 和 y 刻度 x1grid = arange(min1, max1, 0.1) x2grid = arange(min2, max2, 0.1) |
现在我们需要将其转换为网格。
我们可以使用 meshgrid() NumPy 函数从这两个向量创建网格。
如果第一个特征 x1 是我们特征空间的 x 轴,那么对于 y 轴上的每个点,我们需要网格的 x1 值的一行。
同样,如果我们将 x2 作为特征空间的 y 轴,那么对于 x 轴上的每个点,我们需要网格的 x2 值的一列。
_meshgrid()_ 函数将为我们完成此操作,根据需要复制行和列。它返回两个网格,用于两个输入向量。第一个是 x 值网格,第二个是 y 值网格,以适当大小的行和列网格在特征空间中组织。
|
1 2 3 |
... # 创建网格的所有行和列 xx, yy = meshgrid(x1grid, x2grid) |
然后我们需要展平网格以创建可以输入模型并进行预测的样本。
为此,首先,我们将每个网格展平为向量。
|
1 2 3 4 |
... # 将每个网格展平为向量 r1, r2 = xx.flatten(), yy.flatten() r1, r2 = r1.reshape((len(r1), 1)), r2.reshape((len(r2), 1)) |
然后我们将向量并排堆叠作为输入数据集中的列,例如,像我们原始的训练数据集一样,但分辨率更高。
|
1 2 3 |
... # 将向量水平堆叠以创建模型的 x1,x2 输入 grid = hstack((r1,r2)) |
然后我们可以将其输入到我们的模型中,并获得网格中每个点的预测。
|
1 2 3 4 |
... # 对网格进行预测 yhat = model.predict(grid) # 将预测结果重塑回网格 |
到目前为止,一切顺利。
我们有一个特征空间上的值网格和模型预测的类别标签。
接下来,我们需要将值网格绘制为等高线图。
contourf() 函数为每个轴采用单独的网格,就像我们之前调用 _meshgrid()_ 返回的那样。太棒了!
因此,我们可以使用我们之前准备的 _xx_ 和 _yy_,并简单地将模型的预测(_yhat_)重塑为相同的形状。
|
1 2 3 |
... # 将预测结果重塑回网格 zz = yhat.reshape(xx.shape) |
然后我们用两种颜色的颜色映射绘制决策面。
|
1 2 3 |
... # 将 x、y 和 z 值的网格绘制成曲面 pyplot.contourf(xx, yy, zz, cmap='Paired') |
然后我们可以在顶部绘制数据集的实际点,以查看它们如何被逻辑回归决策面很好地分离。
下面列出了在我们的合成二元分类数据集上为逻辑回归模型绘制决策面的完整示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
# 二元分类数据集上逻辑回归的决策面 from numpy import where from numpy import meshgrid from numpy import arange from numpy import hstack from sklearn.datasets import make_blobs from sklearn.linear_model import LogisticRegression from matplotlib import pyplot # 生成数据集 X, y = make_blobs(n_samples=1000, centers=2, n_features=2, random_state=1, cluster_std=3) # 定义域的边界 min1, max1 = X[:, 0].min()-1, X[:, 0].max()+1 min2, max2 = X[:, 1].min()-1, X[:, 1].max()+1 # 定义 x 和 y 刻度 x1grid = arange(min1, max1, 0.1) x2grid = arange(min2, max2, 0.1) # 创建网格的所有行和列 xx, yy = meshgrid(x1grid, x2grid) # 将每个网格展平为向量 r1, r2 = xx.flatten(), yy.flatten() r1, r2 = r1.reshape((len(r1), 1)), r2.reshape((len(r2), 1)) # 将向量水平堆叠以创建模型的 x1,x2 输入 grid = hstack((r1,r2)) # 定义模型 model = LogisticRegression() # 拟合模型 model.fit(X, y) # 对网格进行预测 yhat = model.predict(grid) # 将预测结果重塑回网格 zz = yhat.reshape(xx.shape) # 将 x、y 和 z 值的网格绘制成曲面 pyplot.contourf(xx, yy, zz, cmap='Paired') # 为每个类别的样本创建散点图 for class_value in range(2): # 获取具有此类别的样本的行索引 row_ix = where(y == class_value) # 创建这些样本的散点图 pyplot.scatter(X[row_ix, 0], X[row_ix, 1], cmap='Paired') # 显示绘图 pyplot.show() |
运行示例会拟合模型,并使用它预测特征空间中网格值的输出,然后将结果绘制为等高线图。
正如我们可能怀疑的那样,我们可以看到逻辑回归使用直线划分特征空间。毕竟,它是一个线性模型;这是它唯一能做的。
创建决策面几乎像魔法一样。它立即提供有意义的洞察,了解模型如何学习任务。
尝试使用不同的算法,例如 SVM 或决策树。
在下面的评论中以链接形式发布您生成的地圖!

二元分类任务中逻辑回归的决策面
我们可以通过使用模型预测概率而不是类别标签来增加决策面的深度。
|
1 2 3 4 5 |
... # 对网格进行预测 yhat = model.predict_proba(grid) # 只保留类别 0 的概率 yhat = yhat[:, 0] |
绘制后,我们可以看到特征空间中的每个点属于每个类别标签的置信度或可能性,如模型所示。
我们可以使用不同的颜色图,它具有渐变,并显示图例,以便我们可以解释颜色。
|
1 2 3 4 5 |
... # 将 x、y 和 z 值的网格绘制成曲面 c = pyplot.contourf(xx, yy, zz, cmap='RdBu') # 添加图例,称为颜色条 pyplot.colorbar(c) |
下面列出了使用概率创建决策面的完整示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 |
# 二元分类数据集上逻辑回归的概率决策面 from numpy import where from numpy import meshgrid from numpy import arange from numpy import hstack from sklearn.datasets import make_blobs from sklearn.linear_model import LogisticRegression from matplotlib import pyplot # 生成数据集 X, y = make_blobs(n_samples=1000, centers=2, n_features=2, random_state=1, cluster_std=3) # 定义域的边界 min1, max1 = X[:, 0].min()-1, X[:, 0].max()+1 min2, max2 = X[:, 1].min()-1, X[:, 1].max()+1 # 定义 x 和 y 刻度 x1grid = arange(min1, max1, 0.1) x2grid = arange(min2, max2, 0.1) # 创建网格的所有行和列 xx, yy = meshgrid(x1grid, x2grid) # 将每个网格展平为向量 r1, r2 = xx.flatten(), yy.flatten() r1, r2 = r1.reshape((len(r1), 1)), r2.reshape((len(r2), 1)) # 将向量水平堆叠以创建模型的 x1,x2 输入 grid = hstack((r1,r2)) # 定义模型 model = LogisticRegression() # 拟合模型 model.fit(X, y) # 对网格进行预测 yhat = model.predict_proba(grid) # 只保留类别 0 的概率 yhat = yhat[:, 0] # 将预测结果重塑回网格 zz = yhat.reshape(xx.shape) # 将 x、y 和 z 值的网格绘制成曲面 c = pyplot.contourf(xx, yy, zz, cmap='RdBu') # 添加图例,称为颜色条 pyplot.colorbar(c) # 为每个类别的样本创建散点图 for class_value in range(2): # 获取具有此类别的样本的行索引 row_ix = where(y == class_value) # 创建这些样本的散点图 pyplot.scatter(X[row_ix, 0], X[row_ix, 1], cmap='Paired') # 显示绘图 pyplot.show() |
运行示例会预测特征空间中网格上每个点的类别成员概率,并绘制结果。
在这里,我们可以看到模型在域的中间部分不确定(颜色较浅),因为该特征空间区域存在采样噪声。我们还可以看到模型在域的左下半部分和右上半部分非常自信(颜色饱满)。
清晰的类别和概率决策面共同构成了强大的诊断工具,用于理解您的模型以及它如何为您的预测建模任务划分特征空间。
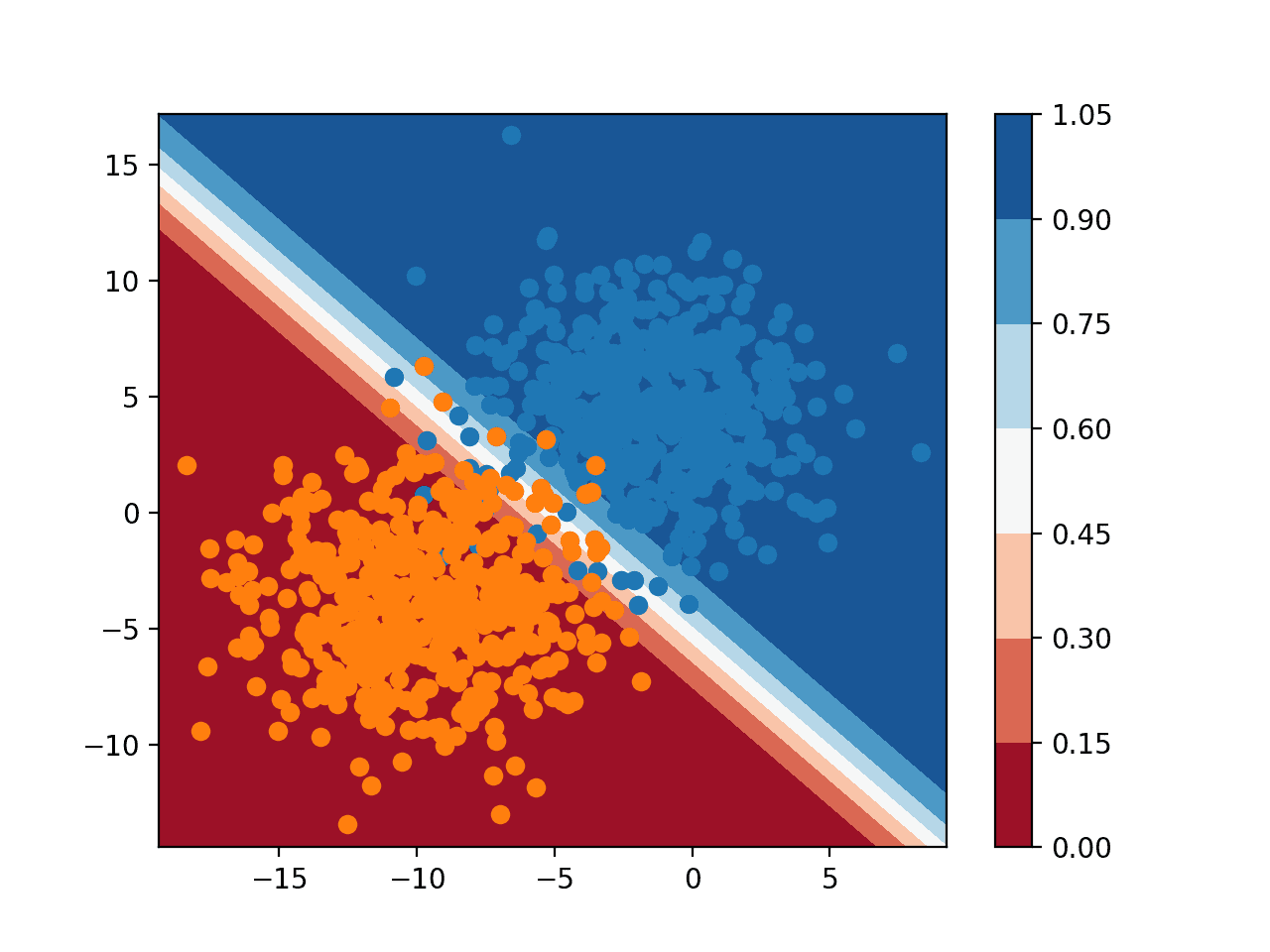
二元分类任务中逻辑回归的概率决策面
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
总结
在本教程中,您学习了如何为分类机器学习算法绘制决策面。
具体来说,你学到了:
- 决策面是一种诊断工具,用于理解分类算法如何划分特征空间。
- 如何使用清晰的类别标签为机器学习算法绘制决策面。
- 如何使用预测概率绘制和解释决策面。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。







很棒的教程!
在过去一年中,我一直在使用一系列计算成本相当高的 for 循环函数执行类似的任务,这里的代码似乎大大加快了我的旧代码!
谢谢 Jason
谢谢!很高兴听到它有用。
您好,我们如何对决策树和螺旋数据集执行相同的操作。
感谢您精彩的教程,非常有帮助!
有没有计划提供包含三个或更多特征的教程?那会非常有趣。或者您有什么阅读建议吗?
不客气。
如果特征超过 2 个,您需要为每对输入变量创建一个曲面图。
和往常一样,Jason 的作品很棒。
您能否提供关于数据发现和编目的简单明了的读物。
还有一件事,请问,
数据源 API
此致
谢谢。
什么是“数据发现和编目”?
感谢这堂精彩的课!
不客气。
感谢这个很棒的教程!
我在 Google 上搜索了一个创建决策面的库模块,发现了这个
https://towardsdatascience.com/easily-visualize-scikit-learn-models-decision-boundaries-dd0fb3747508
我将该模块重命名为 plot_decision_boundaries.py,因为 python 不接受原始名称。有了它,并将文件放在我当前的目录中,我就可以执行以下 python 代码了
from numpy import where
from matplotlib import pyplot
from sklearn.datasets import make_blobs
from sklearn.linear_model import LogisticRegression
from plot_decision_boundaries import plot_decision_boundaries
# 生成数据集
X, y = make_blobs(n_samples=1000, centers=2, n_features=2, random_state=1, cluster_std=3)
fig = pyplot.figure()
plot_decision_boundaries(X, y, LogisticRegression)
pyplot.savefig(‘plot_decision_boundaries_1.png’)
pyplot.close(fig=’all’)
干得不错。
尊敬的Jason博士,
对我来说,创建网格并使用网格值进行预测是其中最“复杂”的操作。虽然您可以在以下位置找到关于 arange 和 meshgrid 的帮助文件:
我将用虚构数据来解释上述操作,以便理解数据结构。可能会涉及到伪代码。
总而言之,了解特征数组 (X) 如何转换为网格,然后转换为网格,有助于我们理解网格如何馈送到模型中以预测决策面的坐标。决策面的颜色由 xx 确定,并馈送到 contourf 函数中。
我将用鸢尾花数据进行实验。该项目将根据花瓣长度与花瓣宽度,以及萼片长度与萼片宽度分为两幅图。
谢谢你,
悉尼的Anthony
干得不错。
你好,
我尝试了上述 Python 代码,效果很好。
问题
如何将这些代码行链接到 CSV 文件?
好问题,这会有帮助
https://machinelearning.org.cn/how-to-connect-model-input-data-with-predictions-for-machine-learning/
非常有趣!
我该如何更改代码,以便每个类别都用不同的标记绘制?比如说橙色用标记“+”,蓝色用标记“o”?
你好,Murilo,
请参考以下内容
https://matplotlib.net.cn/stable/api/markers_api.html
此致,
对于具有三个类别的 softmax 回归,我应该进行哪些更改?
你好 San……你可能会发现以下资源很有用
https://machinelearning.org.cn/multinomial-logistic-regression-with-python/
https://towardsdatascience.com/multiclass-classification-with-softmax-regression-explained-ea320518ea5d