神经网络的训练过程是一个具有挑战性的优化过程,它常常会失败,无法收敛。
这意味着训练结束时的模型可能不是用于最终模型的稳定或表现最佳的一组权重。
解决此问题的一种方法是使用训练过程中后期多个模型权重的平均值。这被称为 Polyak-Ruppert 平均,可以通过使用模型权重线性或指数递减的加权平均来进一步改进。除了产生更稳定的模型外,平均模型权重的性能也可以带来更好的性能。
在本教程中,您将了解如何将多个不同模型的权重合并到一个模型中以进行预测。
完成本教程后,您将了解:
- 神经网络训练的随机性和挑战性可能意味着优化过程不会收敛。
- 通过对训练过程中观察到的模型权重的平均值创建模型,可以获得更稳定、有时性能更好的解决方案。
- 如何开发由多个已保存模型中的模型参数等权重、线性加权和指数加权平均创建的最终模型。
用我的新书《更好的深度学习》来启动你的项目,书中包含分步教程和所有示例的 Python 源代码文件。
让我们开始吧。
- 2019 年 10 月更新:更新至 Keras 2.3 和 TensorFlow 2.0。
- **2020年1月更新**:已针对 scikit-learn v0.22 API 的变更进行更新。

如何在 Keras 中创建神经网络模型权重的等权重、线性加权和指数加权平均
照片由 netselesoobrazno 提供,保留部分权利。
教程概述
本教程分为七个部分,它们是:
- 平均模型权重集成
- 多类别分类问题
- 多层感知器模型
- 将多个模型保存到文件
- 具有平均模型权重的模型
- 使用平均模型权重集成进行预测
- 线性与指数递减加权平均
平均模型权重集成
学习深度神经网络模型的权重需要解决高维非凸优化问题。
解决此优化问题的一个挑战是存在许多“好”的解决方案,并且学习算法可能会来回跳跃而无法固定在其中一个上。在随机优化领域,这被称为优化算法在解决方案上的收敛问题,其中解决方案由一组特定的权重值定义。
如果您遇到模型收敛问题,可能会看到一个症状,即训练和/或测试损失值显示出比预期更高的方差,例如,它在训练周期中会剧烈波动或上下跳动。
解决此问题的一种方法是组合在训练过程结束时收集的权重。通常,这可能被称为时间平均,并被称为 Polyak 平均或 Polyak-Ruppert 平均,以该方法最初的开发者命名。
Polyak 平均包括对优化算法访问的参数空间轨迹中的几个点进行平均。
— 第 322 页,深度学习,2016。
在学习过程中平均多个有噪声的权重集,听起来可能比调整优化过程本身更不理想,但可能会被证明是一个理想的解决方案,特别是对于可能需要花费数天、数周甚至数月才能训练的大型神经网络。
基础性的进步是基于一个看似矛盾的想法实现的:平均收敛速率较低的慢速算法。
— 通过平均加速随机近似,1992。
平均单个训练运行中的多个模型权重,可以平滑掉由于学习超参数(例如学习率)的选择或正在学习的映射函数的形状而可能产生的噪声优化过程。结果是一个最终模型或一组权重,它可能提供更稳定、或许更准确的结果。
基本思想是,优化算法可能会在山谷两侧来回跳跃数次,而从未到达山谷底部附近。然而,两侧所有位置的平均值应该接近山谷底部。
— 第 322 页,深度学习,2016。
Polyak-Ruppert 平均最简单的实现方法是计算训练后期模型权重的平均值。
可以通过计算加权平均值来改进这一点,其中对更近期的模型应用更多的权重,该权重在先前周期中呈线性递减。另一种更常用的方法是使用加权平均的指数衰减。
Polyak-Ruppert 平均已被证明可以改善标准 SGD 的收敛性 [...]。或者,可以使用参数的指数移动平均,为最近的参数值赋予更高的权重。
— Adam:一种随机优化方法,2014。
在最终模型中使用模型权重的平均值或加权平均值是确保从训练运行中获得最佳结果的常用技术。该方法是 Google Inception V2 和 V3 深度卷积神经网络模型中用于照片分类的众多“技巧”之一,这是深度学习领域的一个里程碑。
模型评估使用随时间计算的参数的运行平均值进行。
— 重新思考用于计算机视觉的 Inception 架构,2015。
想要通过深度学习获得更好的结果吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
多类别分类问题
我们将使用一个小型的多类分类问题作为演示模型权重集成的基础。
scikit-learn 类提供了 make_blobs() 函数,可用于创建具有指定样本数、输入变量、类别和类别内样本方差的多类分类问题。
该问题有两个输入变量(用于表示点的x和y坐标),并且每个组内点的标准差为 2.0。我们将使用相同的随机状态(伪随机数生成器的种子)来确保我们始终获得相同的数据点。
|
1 2 |
# 生成二维分类数据集 X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2) |
结果是我们可以建模的数据集的输入和输出元素。
为了了解问题的复杂性,我们可以在二维散点图上绘制每个点,并根据类别值对每个点进行着色。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# blob 数据集的散点图 from sklearn.datasets import make_blobs from matplotlib import pyplot from numpy import where # 生成二维分类数据集 X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2) # 每个类别值的散点图 for class_value in range(3): # 选择具有类标签的点的索引 row_ix = where(y == class_value) # 绘制不同颜色点的散点图 pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # 显示图 pyplot.show() |
运行此示例将生成整个数据集的散点图。我们可以看到,标准差为 2.0 意味着这些类不是线性可分的(不能用一条线分开),导致许多模糊的点。
这是可取的,因为它意味着问题并非微不足道,并且可以让神经网络模型找到许多不同的“足够好”的候选解决方案,从而产生高方差。
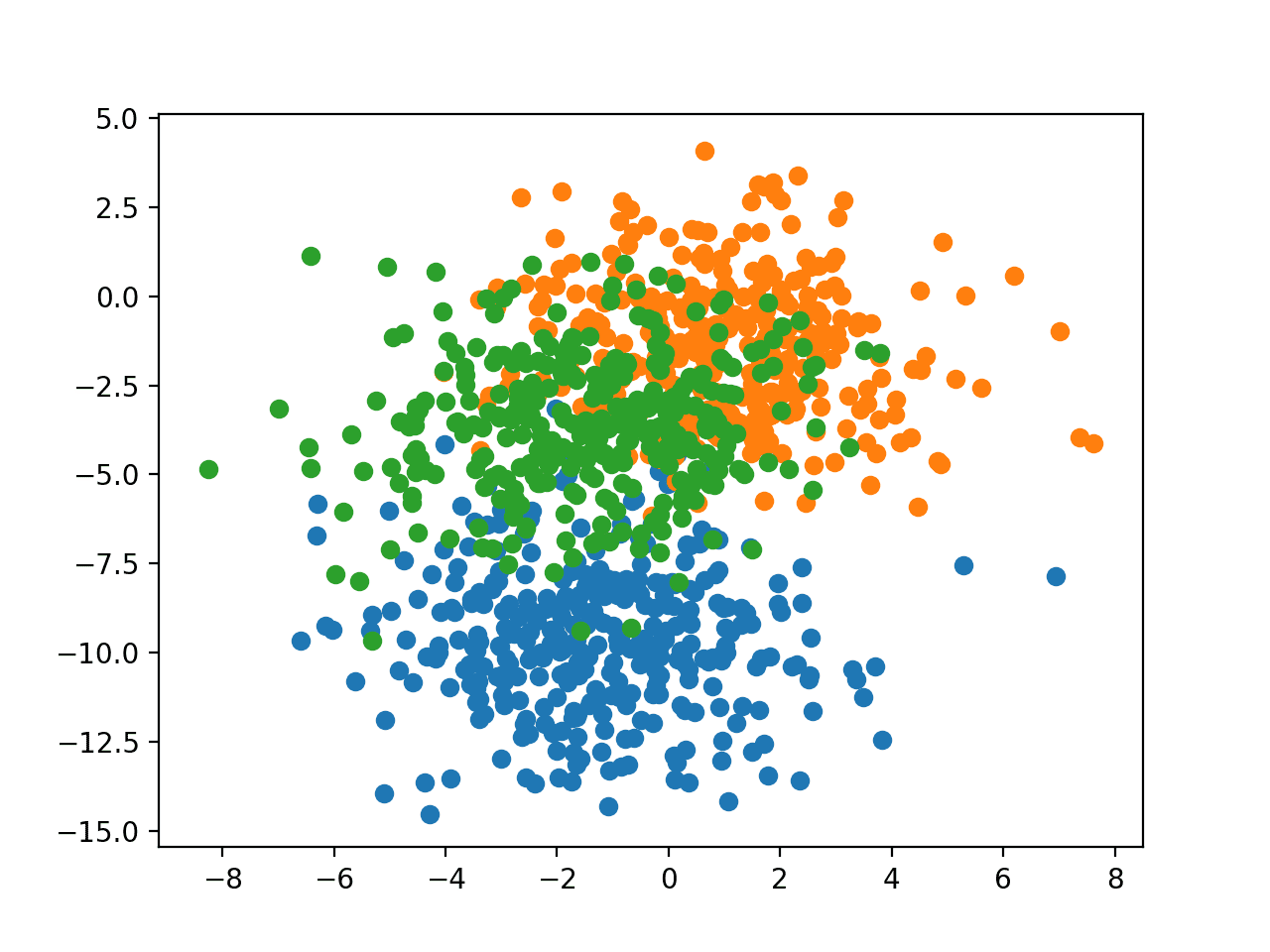
具有三个类别且点按类别值着色的 Blob 数据集散点图
多层感知器模型
在定义模型之前,我们需要设计一个适合集成的任务。
在我们的问题中,训练数据集相对较小。具体来说,训练数据集中的样本与保留数据集的比例为 10:1。这模拟了我们可能拥有大量未标记示例和少量标记示例来训练模型的情况。
我们将从斑点问题中创建 1100 个数据点。模型将在前 100 个点上进行训练,其余 1000 个将保留在测试数据集中,模型无法使用。
该问题是一个多类分类问题,我们将使用输出层上的 softmax 激活函数对其进行建模。这意味着模型将预测一个包含三个元素的向量,表示样本属于三个类别中每个类别的概率。因此,在我们将行分割为训练和测试数据集之前,必须对类别值进行独热编码。我们可以使用 Keras 的to_categorical()函数来做到这一点。
|
1 2 3 4 5 6 7 8 |
# 生成二维分类数据集 X, y = make_blobs(n_samples=1100, centers=3, n_features=2, cluster_std=2, random_state=2) # 独热编码输出变量 y = to_categorical(y) # 分割成训练集和测试集 n_train = 100 trainX, testX = X[:n_train, :], X[n_train:, :] trainy, testy = y[:n_train], y[n_train:] |
接下来,我们可以定义并编译模型。
模型将需要两个输入变量的样本。然后,模型有一个具有 25 个节点的单个隐藏层和 ReLU 激活函数,然后是一个具有三个节点以预测每个类别概率的输出层,并带有 softmax 激活函数。
由于问题是多类的,我们将使用分类交叉熵损失函数来优化模型,并使用带有较小学习率和动量的随机梯度下降。
|
1 2 3 4 5 6 |
# 定义模型 model = Sequential() model.add(Dense(25, input_dim=2, activation='relu')) model.add(Dense(3, activation='softmax')) opt = SGD(lr=0.01, momentum=0.9) model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy']) |
模型将进行 500 个训练周期,我们将在每个周期在测试集上评估模型,将测试集用作验证集。
|
1 2 |
# 拟合模型 history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=500, verbose=0) |
运行结束时,我们将评估模型在训练集和测试集上的性能。
|
1 2 3 4 |
# 评估模型 _, train_acc = model.evaluate(trainX, trainy, verbose=0) _, test_acc = model.evaluate(testX, testy, verbose=0) print('Train: %.3f, Test: %.3f' % (train_acc, test_acc)) |
最后,我们将绘制模型在训练集和验证集上每个训练周期的准确率学习曲线。
|
1 2 3 4 5 |
# 模型准确率的学习曲线 pyplot.plot(history.history['accuracy'], label='train') pyplot.plot(history.history['val_accuracy'], label='test') pyplot.legend() pyplot.show() |
将所有这些联系在一起,完整的示例如下。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
# 为 blob 数据集开发一个 mlp from sklearn.datasets import make_blobs from keras.utils import to_categorical from keras.models import Sequential from keras.layers import Dense from keras.optimizers import SGD from matplotlib import pyplot # 生成二维分类数据集 X, y = make_blobs(n_samples=1100, centers=3, n_features=2, cluster_std=2, random_state=2) # 独热编码输出变量 y = to_categorical(y) # 分割成训练集和测试集 n_train = 100 trainX, testX = X[:n_train, :], X[n_train:, :] trainy, testy = y[:n_train], y[n_train:] # 定义模型 model = Sequential() model.add(Dense(25, input_dim=2, activation='relu')) model.add(Dense(3, activation='softmax')) opt = SGD(lr=0.01, momentum=0.9) model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy']) # 拟合模型 history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=500, verbose=0) # 评估模型 _, train_acc = model.evaluate(trainX, trainy, verbose=0) _, test_acc = model.evaluate(testX, testy, verbose=0) print('Train: %.3f, Test: %.3f' % (train_acc, test_acc)) # 模型准确率的学习曲线 pyplot.plot(history.history['accuracy'], label='train') pyplot.plot(history.history['val_accuracy'], label='test') pyplot.legend() pyplot.show() |
运行示例会打印出最终模型在训练集和测试集上的性能。
注意:由于算法或评估程序的随机性,或者数值精度的差异,您的结果可能有所不同。请考虑运行示例几次并比较平均结果。
在这种情况下,我们可以看到模型在训练集上达到了约 86% 的准确率,我们知道这是乐观的,在测试集上达到了约 81% 的准确率,我们预期这会更现实。
|
1 |
训练:0.860,测试:0.812 |
还创建了一条线图,显示了模型在训练集和测试集上每个训练周期的准确率学习曲线。
我们可以看到,在大部分训练过程中,训练准确率都比测试准确率更乐观,正如我们在最终分数中也注意到的那样。重要的是,我们在训练期间的训练和测试数据集上的准确率都有相当大的方差,这可能为使用模型权重平均提供了一个良好的基础。
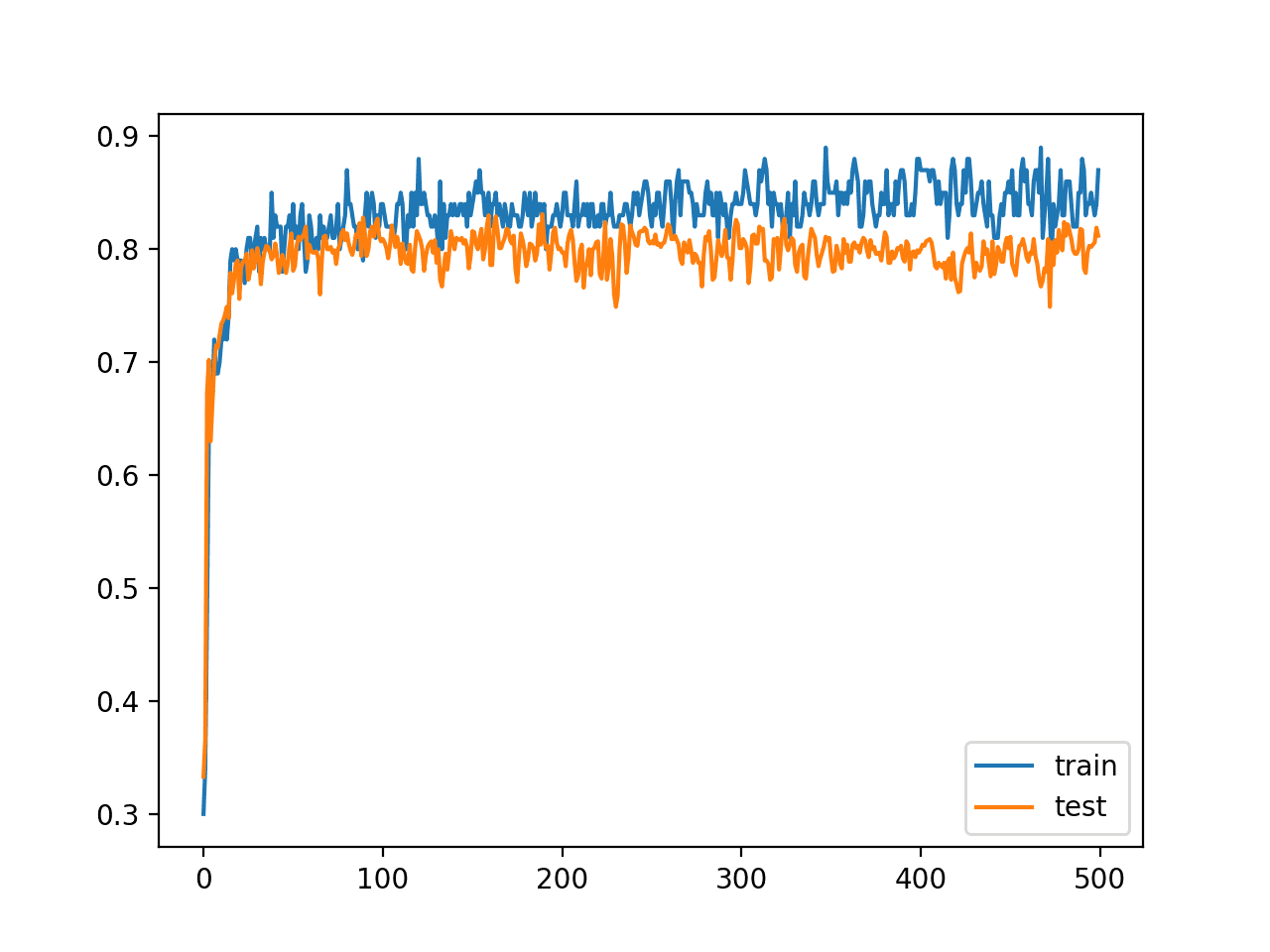
绘制每个训练周期中模型在训练集和测试集上的准确率学习曲线
将多个模型保存到文件
模型权重集成的一种方法是保持模型权重的运行平均值在内存中。
这种方法有三个缺点:
- 它要求您预先知道模型权重将如何组合;也许您想尝试不同的方法。
- 它要求您知道训练的训练周期数;也许您想使用提前停止。
- 它要求您将至少一个完整的网络副本保留在内存中;对于大型模型来说,这可能非常昂贵,如果训练过程崩溃或被终止,则非常脆弱。
另一种方法是作为第一步在训练过程中将模型权重保存到文件,然后稍后组合来自已保存模型的权重以创建最终模型。
也许最简单的实现方法是逐个周期地手动驱动训练过程,然后在超出训练周期数量上限的情况下,在周期结束时保存模型。
例如,对于我们的测试问题,我们将训练模型 500 个周期,并可能从第 490 个周期开始保存模型(例如,在第 490 个和第 499 个周期之间,包括两者)。
|
1 2 3 4 5 6 7 8 |
# 拟合模型 n_epochs, n_save_after = 500, 490 for i in range(n_epochs): # 拟合模型一个周期 model.fit(trainX, trainy, epochs=1, verbose=0) # 检查是否应保存模型 if i >= n_save_after: model.save('model_' + str(i) + '.h5') |
可以使用模型上的save()函数将模型保存到文件,并指定包含周期号的文件名。
请注意,在 Keras 中保存和加载神经网络模型需要安装 h5py 库。您可以使用 pip 如下安装此库:
|
1 |
pip install h5py |
将所有这些内容联系起来,训练模型并在训练数据集上进行拟合并保存最后 10 个周期的所有模型的完整示例,如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
# 将模型保存到训练运行末尾的文件 from sklearn.datasets import make_blobs from keras.utils import to_categorical from keras.models import Sequential from keras.layers import Dense # 生成二维分类数据集 X, y = make_blobs(n_samples=1100, centers=3, n_features=2, cluster_std=2, random_state=2) # 独热编码输出变量 y = to_categorical(y) # 分割成训练集和测试集 n_train = 100 trainX, testX = X[:n_train, :], X[n_train:, :] trainy, testy = y[:n_train], y[n_train:] # 定义模型 model = Sequential() model.add(Dense(25, input_dim=2, activation='relu')) model.add(Dense(3, activation='softmax')) model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy']) # 拟合模型 n_epochs, n_save_after = 500, 490 for i in range(n_epochs): # 拟合模型一个周期 model.fit(trainX, trainy, epochs=1, verbose=0) # 检查是否应保存模型 if i >= n_save_after: model.save('model_' + str(i) + '.h5') |
运行示例将在当前工作目录中保存 10 个模型。
具有平均模型权重的模型
我们可以从具有相同体系结构的多个现有模型创建新模型。
首先,我们需要将模型加载到内存中。这还是合理的,因为模型很小。如果您处理的是非常大的模型,那么一次加载一个模型并在内存中平均权重可能会更容易。
Keras 的load_model() 函数可用于从文件加载已保存的模型。下面的load_all_models()函数将从当前工作目录加载模型。它将开始和结束周期作为参数,以便您可以尝试保存的连续周期的不同模型组。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# 从文件加载模型 def load_all_models(n_start, n_end): all_models = list() for epoch in range(n_start, n_end): # 为此集成模型定义文件名 filename = 'model_' + str(epoch) + '.h5' # 从文件加载模型 model = load_model(filename) # 添加到成员列表 all_models.append(model) print('>loaded %s' % filename) return all_models |
我们可以调用该函数来加载所有模型。
|
1 2 3 |
# 按顺序加载模型 members = load_all_models(490, 500) print('Loaded %d models' % len(members)) |
加载后,我们可以创建具有模型权重加权平均的新模型。
每个模型都有一个get_weights()函数,它返回一个数组列表,每个模型中的每个层一个。我们可以枚举模型中的每个层,检索每个模型中的同一层,并计算加权平均值。这将为我们提供一组权重。
然后,我们可以使用clone_model() Keras 函数来克隆体系结构,并调用set_weights()函数来使用我们准备好的平均权重。下面的model_weight_ensemble()函数实现了这一点。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# 从多个模型的权重创建模型 def model_weight_ensemble(members, weights): # 确定需要平均的层数 n_layers = len(members[0].get_weights()) # 创建一组平均模型权重 avg_model_weights = list() for layer in range(n_layers): # 从每个模型收集这一层 layer_weights = array([model.get_weights()[layer] for model in members]) # 此层的权重加权平均 avg_layer_weights = average(layer_weights, axis=0, weights=weights) # 存储平均层权重 avg_model_weights.append(avg_layer_weights) # 创建一个具有相同结构的全新模型 model = clone_model(members[0]) # 在新模型中设置权重 model.set_weights(avg_model_weights) model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy']) return model |
将这些元素结合起来,我们可以加载 10 个模型并计算模型权重的等权重(算术平均值)。完整的列表如下。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 |
# 对多个加载模型的权重进行平均 from keras.models import load_model from keras.models import clone_model from numpy import average from numpy import array # 从文件加载模型 def load_all_models(n_start, n_end): all_models = list() for epoch in range(n_start, n_end): # 为此集成模型定义文件名 filename = 'model_' + str(epoch) + '.h5' # 从文件加载模型 model = load_model(filename) # 添加到成员列表 all_models.append(model) print('>loaded %s' % filename) return all_models # 从多个模型的权重创建模型 def model_weight_ensemble(members, weights): # 确定需要平均的层数 n_layers = len(members[0].get_weights()) # 创建一组平均模型权重 avg_model_weights = list() for layer in range(n_layers): # 从每个模型收集这一层 layer_weights = array([model.get_weights()[layer] for model in members]) # 此层的权重加权平均 avg_layer_weights = average(layer_weights, axis=0, weights=weights) # 存储平均层权重 avg_model_weights.append(avg_layer_weights) # 创建一个具有相同结构的全新模型 model = clone_model(members[0]) # 在新模型中设置权重 model.set_weights(avg_model_weights) model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy']) return model # 将所有模型加载到内存中 members = load_all_models(490, 500) print('Loaded %d models' % len(members)) # 准备一个等权重数组 n_models = len(members) 权重 = [1/n_models for i in range(1, n_models+1)] # 创建一个由所有模型权重加权平均而成的新模型 model = model_weight_ensemble(members, weights) # 总结创建的模型 model.summary() |
运行示例首先会从文件中加载 10 个模型。
|
1 2 3 4 5 6 7 8 9 10 11 |
> loaded model_490.h5 > loaded model_491.h5 > loaded model_492.h5 > loaded model_493.h5 > loaded model_494.h5 > loaded model_495.h5 > loaded model_496.h5 > loaded model_497.h5 > loaded model_498.h5 > loaded model_499.h5 已加载 10 个模型 |
基于这 10 个模型创建了一个模型权重集成,每个模型具有相等的权重,并报告了模型结构的摘要。
|
1 2 3 4 5 6 7 8 9 10 11 |
_________________________________________________________________ 层(类型) 输出形状 参数数量 ================================================================= dense_1 (Dense) (None, 25) 75 _________________________________________________________________ dense_2 (Dense) (None, 3) 78 ================================================================= 总参数:153 可训练参数:153 不可训练参数: 0 _________________________________________________________________ |
使用平均模型权重集成进行预测
现在我们知道了如何计算模型权重的加权平均,我们可以用得到的模型来评估预测。
一个问题是我们不知道有多少模型适合组合以获得良好的性能。我们可以通过评估模型权重平均集成最近 n 个模型来解决这个问题,并改变 n 来查看有多少模型能获得良好的性能。
下面的 `evaluate_n_members()` 函数将从给定数量的已加载模型创建一个新模型。每个模型在最终模型的贡献中都具有相等的权重,然后调用 `model_weight_ensemble()` 函数来创建最终模型,并对测试数据集进行评估。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
# 评估集成中的特定数量成员 def evaluate_n_members(members, n_members, testX, testy): # 反转已加载的模型,以便我们先构建最后一个模型的集成 members = list(reversed(members)) # 选择成员子集 subset = members[:n_members] # 准备一个等权重数组 weights = [1.0/n_members for i in range(1, n_members+1)] # 创建一个由所有模型权重加权平均而成的新模型 model = model_weight_ensemble(subset, weights) # 进行预测并评估准确率 _, test_acc = model.evaluate(testX, testy, verbose=0) return test_acc |
重要的是,首先反转已加载的模型列表,以确保使用训练过程中最后 n 个模型,我们假定这些模型可能平均性能更好。
|
1 2 |
# 反转已加载的模型,以便我们先构建最后一个模型的集成 members = list(reversed(members)) |
然后,我们可以评估由训练过程中保存的最后 n 个模型中的不同数量的模型创建的模型,从最后一个模型到最后 10 个模型。除了评估组合的最终模型外,我们还可以评估每个单独保存的模型在测试数据集上的性能以进行比较。
|
1 2 3 4 5 6 7 8 9 10 11 |
# 在保留集上评估不同数量的集成 single_scores, ensemble_scores = list(), list() for i in range(1, len(members)+1): # 评估具有 i 个模型的集成 ensemble_score = evaluate_n_members(members, i, testX, testy) # 单独评估第 i 个模型 _, single_score = members[i-1].evaluate(testX, testy, verbose=0) # 总结这一步 print('> %d: single=%.3f, ensemble=%.3f' % (i, single_score, ensemble_score)) ensemble_scores.append(ensemble_score) single_scores.append(single_score) |
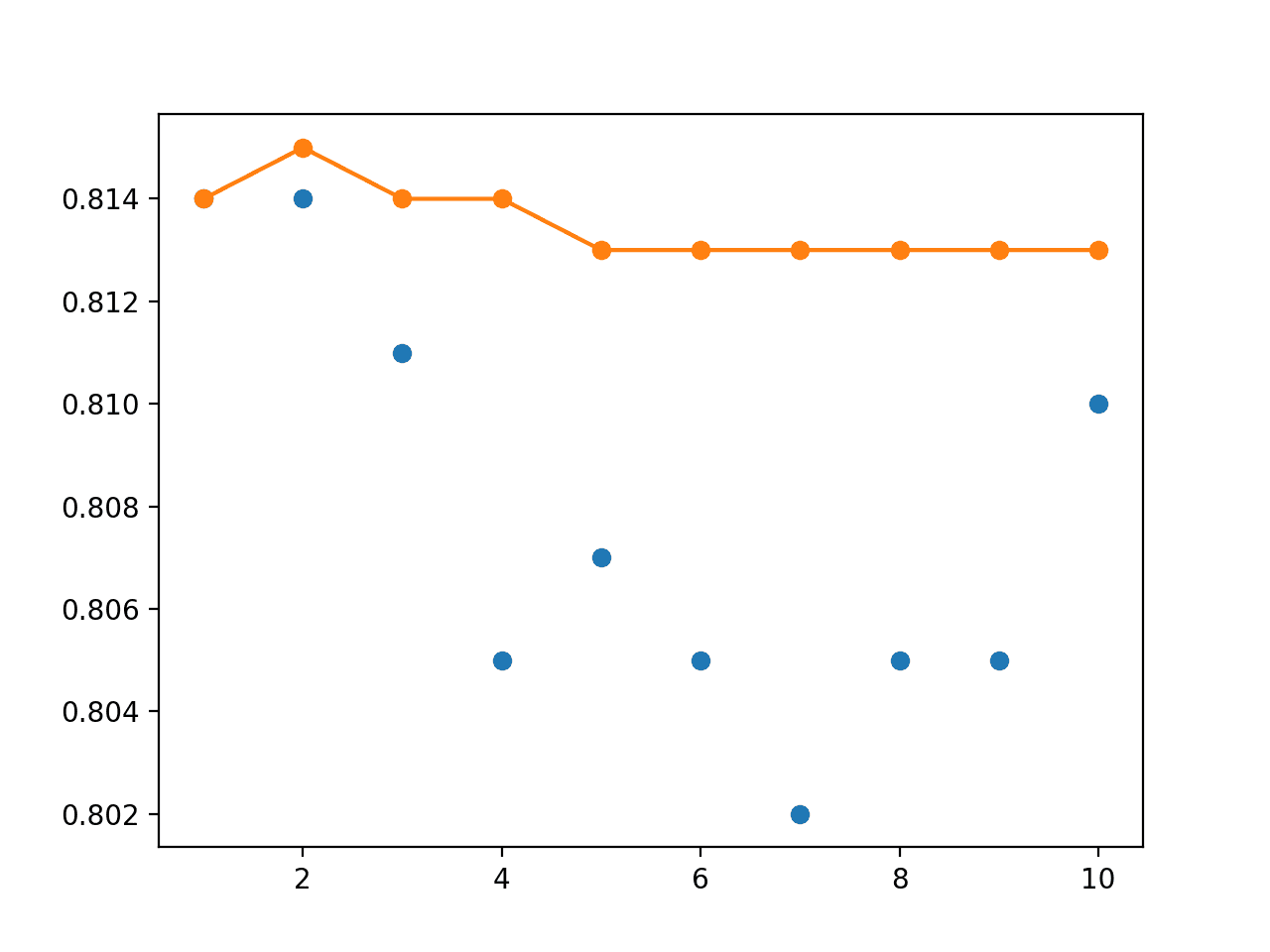
收集到的分数可以绘制出来,其中蓝色点表示单个已保存模型的准确率,橙色线表示组合了从最后 n 个模型直到当前模型的权重进行组合的模型在测试集上的准确率。
|
1 2 3 4 5 |
# 绘制分数与集成成员数量的关系 x_axis = [i for i in range(1, len(members)+1)] pyplot.plot(x_axis, single_scores, marker='o', linestyle='None') pyplot.plot(x_axis, ensemble_scores, marker='o') pyplot.show() |
将所有这些联系在一起,完整的示例如下。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 |
# blobs 问题上的模型权重平均 from sklearn.datasets import make_blobs from sklearn.metrics import accuracy_score from keras.utils import to_categorical from keras.models import load_model from keras.models import clone_model from keras.models import Sequential from keras.layers import Dense from matplotlib import pyplot from numpy import average from numpy import array # 从文件加载模型 def load_all_models(n_start, n_end): all_models = list() for epoch in range(n_start, n_end): # 为此集成模型定义文件名 filename = 'model_' + str(epoch) + '.h5' # 从文件加载模型 model = load_model(filename) # 添加到成员列表 all_models.append(model) print('>loaded %s' % filename) return all_models # # 从多个模型的权重创建一个模型 def model_weight_ensemble(members, weights): # 确定需要平均的层数 n_layers = len(members[0].get_weights()) # 创建一组平均模型权重 avg_model_weights = list() for layer in range(n_layers): # 从每个模型收集这一层 layer_weights = array([model.get_weights()[layer] for model in members]) # 此层的权重加权平均 avg_layer_weights = average(layer_weights, axis=0, weights=weights) # 存储平均层权重 avg_model_weights.append(avg_layer_weights) # 创建一个具有相同结构的全新模型 model = clone_model(members[0]) # 在新模型中设置权重 model.set_weights(avg_model_weights) model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy']) return model # 评估集成中的特定数量成员 def evaluate_n_members(members, n_members, testX, testy): # 选择成员子集 subset = members[:n_members] # 准备一个等权重数组 weights = [1.0/n_members for i in range(1, n_members+1)] # 创建一个由所有模型权重加权平均而成的新模型 model = model_weight_ensemble(subset, weights) # 进行预测并评估准确率 _, test_acc = model.evaluate(testX, testy, verbose=0) return test_acc # 生成二维分类数据集 X, y = make_blobs(n_samples=1100, centers=3, n_features=2, cluster_std=2, random_state=2) # 独热编码输出变量 y = to_categorical(y) # 分割成训练集和测试集 n_train = 100 trainX, testX = X[:n_train, :], X[n_train:, :] trainy, testy = y[:n_train], y[n_train:] # 按顺序加载模型 members = load_all_models(490, 500) print('Loaded %d models' % len(members)) # 反转已加载的模型,以便我们先构建最后一个模型的集成 members = list(reversed(members)) # 在保留集上评估不同数量的集成 single_scores, ensemble_scores = list(), list() for i in range(1, len(members)+1): # 评估具有 i 个模型的集成 ensemble_score = evaluate_n_members(members, i, testX, testy) # 单独评估第 i 个模型 _, single_score = members[i-1].evaluate(testX, testy, verbose=0) # 总结这一步 print('> %d: single=%.3f, ensemble=%.3f' % (i, single_score, ensemble_score)) ensemble_scores.append(ensemble_score) single_scores.append(single_score) # 绘制分数与集成成员数量的关系 x_axis = [i for i in range(1, len(members)+1)] pyplot.plot(x_axis, single_scores, marker='o', linestyle='None') pyplot.plot(x_axis, ensemble_scores, marker='o') pyplot.show() |
运行示例首先会加载 10 个已保存的模型。
|
1 2 3 4 5 6 7 8 9 10 11 |
> loaded model_490.h5 > loaded model_491.h5 > loaded model_492.h5 > loaded model_493.h5 > loaded model_494.h5 > loaded model_495.h5 > loaded model_496.h5 > loaded model_497.h5 > loaded model_498.h5 > loaded model_499.h5 已加载 10 个模型 |
报告了每个单独保存的模型以及一个模型权重集成(其权重是从所有模型(包括每个模型)平均而来,从训练运行的末尾向前工作)的性能。
注意:由于算法或评估程序的随机性,或者数值精度的差异,您的结果可能有所不同。请考虑运行示例几次并比较平均结果。
结果显示,最佳测试准确率约为 81.4%,由最后两个模型实现。我们可以看到,模型权重集成平均化了性能,并且性能同样好。
|
1 2 3 4 5 6 7 8 9 10 |
> 1: single=0.814, ensemble=0.814 > 2: single=0.814, ensemble=0.814 > 3: single=0.811, ensemble=0.813 > 4: single=0.805, ensemble=0.813 > 5: single=0.807, ensemble=0.811 > 6: single=0.805, ensemble=0.807 > 7: single=0.802, ensemble=0.809 > 8: single=0.805, ensemble=0.808 > 9: single=0.805, ensemble=0.808 > 10: single=0.810, ensemble=0.807 |
还创建了一个折线图,显示了每个单个模型的测试准确率(蓝色点)和模型权重集成(橙色线)的性能。
我们可以看到,平均模型权重确实使最终模型的性能趋于平稳,并且性能至少与运行的最后一个模型一样好。
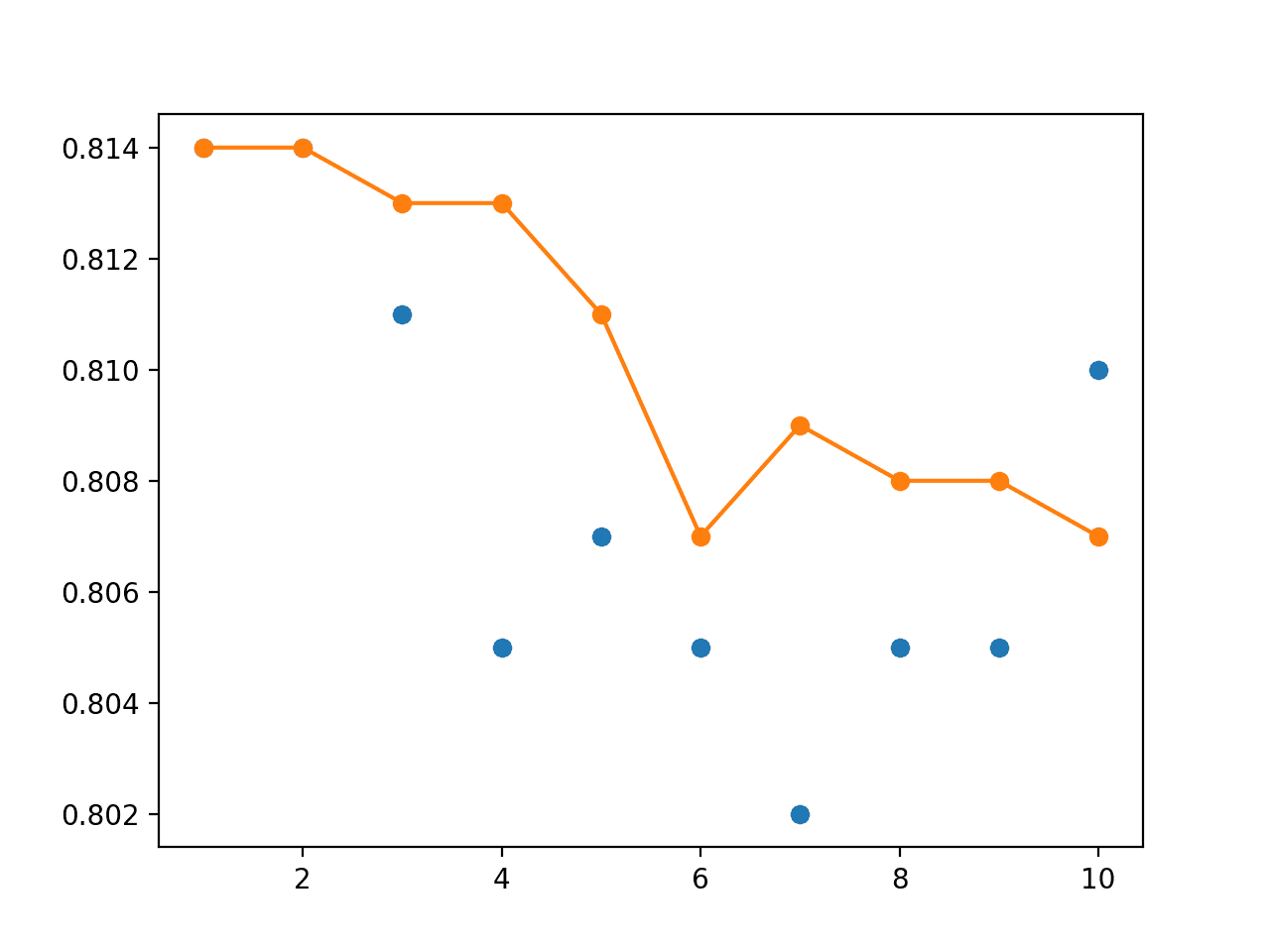
单个模型测试性能(蓝色点)和模型权重集成测试性能(橙色线)的折线图
线性与指数递减加权平均
我们可以更新示例并评估模型权重在集成中的线性递减加权。
权重可计算如下
|
1 2 |
# 准备一个线性递减权重数组 weights = [i/n_members for i in range(n_members, 0, -1)] |
这可以代替 `evaluate_n_members()` 函数中的等权重。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 |
# blobs 问题上模型的线性递减加权平均 from sklearn.datasets import make_blobs from sklearn.metrics import accuracy_score from keras.utils import to_categorical from keras.models import load_model from keras.models import clone_model from keras.models import Sequential from keras.layers import Dense from matplotlib import pyplot from numpy import average from numpy import array # 从文件加载模型 def load_all_models(n_start, n_end): all_models = list() for epoch in range(n_start, n_end): # 为此集成模型定义文件名 filename = 'model_' + str(epoch) + '.h5' # 从文件加载模型 model = load_model(filename) # 添加到成员列表 all_models.append(model) print('>loaded %s' % filename) return all_models # 从多个模型的权重创建模型 def model_weight_ensemble(members, weights): # 确定需要平均的层数 n_layers = len(members[0].get_weights()) # 创建一组平均模型权重 avg_model_weights = list() for layer in range(n_layers): # 从每个模型收集这一层 layer_weights = array([model.get_weights()[layer] for model in members]) # 此层的权重加权平均 avg_layer_weights = average(layer_weights, axis=0, weights=weights) # 存储平均层权重 avg_model_weights.append(avg_layer_weights) # 创建一个具有相同结构的全新模型 model = clone_model(members[0]) # 在新模型中设置权重 model.set_weights(avg_model_weights) model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy']) return model # 评估集成中的特定数量成员 def evaluate_n_members(members, n_members, testX, testy): # 选择成员子集 subset = members[:n_members] # 准备一个线性递减权重数组 weights = [i/n_members for i in range(n_members, 0, -1)] # 创建一个由所有模型权重加权平均而成的新模型 model = model_weight_ensemble(subset, weights) # 进行预测并评估准确率 _, test_acc = model.evaluate(testX, testy, verbose=0) return test_acc # 生成二维分类数据集 X, y = make_blobs(n_samples=1100, centers=3, n_features=2, cluster_std=2, random_state=2) # 独热编码输出变量 y = to_categorical(y) # 分割成训练集和测试集 n_train = 100 trainX, testX = X[:n_train, :], X[n_train:, :] trainy, testy = y[:n_train], y[n_train:] # 按顺序加载模型 members = load_all_models(490, 500) print('Loaded %d models' % len(members)) # 反转已加载的模型,以便我们先构建最后一个模型的集成 members = list(reversed(members)) # 在保留集上评估不同数量的集成 single_scores, ensemble_scores = list(), list() for i in range(1, len(members)+1): # 评估具有 i 个模型的集成 ensemble_score = evaluate_n_members(members, i, testX, testy) # 单独评估第 i 个模型 _, single_score = members[i-1].evaluate(testX, testy, verbose=0) # 总结这一步 print('> %d: single=%.3f, ensemble=%.3f' % (i, single_score, ensemble_score)) ensemble_scores.append(ensemble_score) single_scores.append(single_score) # 绘制分数与集成成员数量的关系 x_axis = [i for i in range(1, len(members)+1)] pyplot.plot(x_axis, single_scores, marker='o', linestyle='None') pyplot.plot(x_axis, ensemble_scores, marker='o') pyplot.show() |
运行示例会再次报告每个单个模型的性能,这次是每个平均模型权重集成在线性递减模型贡献下的测试准确率。
注意:由于算法或评估程序的随机性,或者数值精度的差异,您的结果可能有所不同。请考虑运行示例几次并比较平均结果。
我们可以看到,至少在这种情况下,集成实现了比任何独立模型都稍高的性能,准确率达到约 81.5%。
|
1 2 3 4 5 6 7 8 9 10 11 |
... > 1: single=0.814, ensemble=0.814 > 2: single=0.814, ensemble=0.815 > 3: single=0.811, ensemble=0.814 > 4: single=0.805, ensemble=0.813 > 5: single=0.807, ensemble=0.813 > 6: single=0.805, ensemble=0.813 > 7: single=0.802, ensemble=0.811 > 8: single=0.805, ensemble=0.810 > 9: single=0.805, ensemble=0.809 > 10: single=0.810, ensemble=0.809 |
折线图显示了性能的提升,并且与使用均匀加权的集成相比,在不同大小的集成模型中,测试准确率的性能更加稳定。
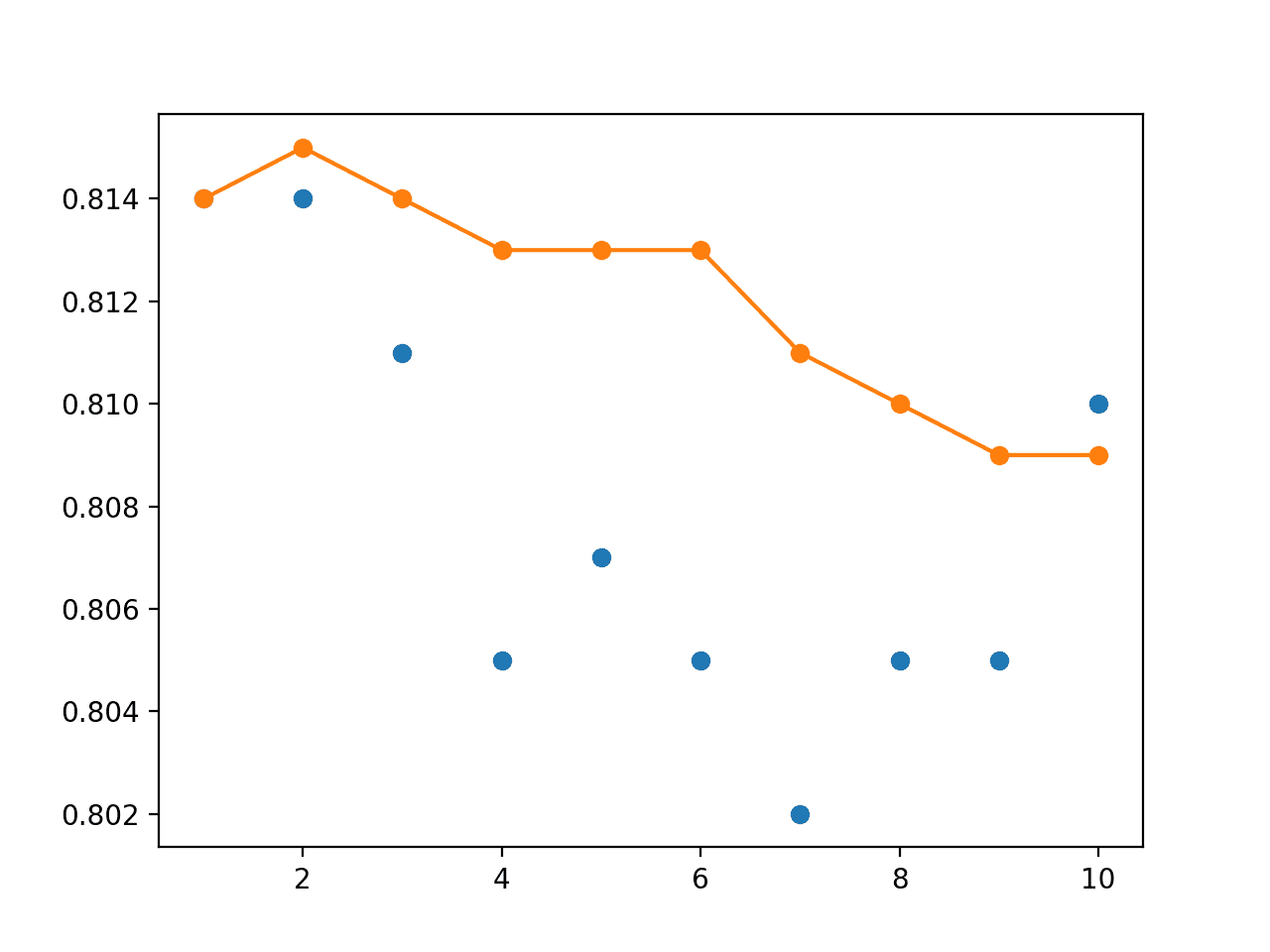
单个模型测试性能(蓝色点)和具有线性衰减的模型权重集成测试性能(橙色线)的折线图
我们还可以尝试模型贡献的指数衰减。这需要指定衰减率(alpha)。下面的示例创建了衰减率为 2 的指数衰减的权重。
|
1 2 3 |
# 准备一个指数递减权重数组 alpha = 2.0 weights = [exp(-i/alpha) for i in range(1, n_members+1)] |
下面列出了包含模型对集成模型平均权重贡献的指数衰减的完整示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 |
# blobs 问题上模型的指数递减加权平均 from sklearn.datasets import make_blobs from sklearn.metrics import accuracy_score from keras.utils import to_categorical from keras.models import load_model from keras.models import clone_model from keras.models import Sequential from keras.layers import Dense from matplotlib import pyplot from numpy import average from numpy import array from math import exp # 从文件加载模型 def load_all_models(n_start, n_end): all_models = list() for epoch in range(n_start, n_end): # 为此集成模型定义文件名 filename = 'model_' + str(epoch) + '.h5' # 从文件加载模型 model = load_model(filename) # 添加到成员列表 all_models.append(model) print('>loaded %s' % filename) return all_models # 从多个模型的权重创建模型 def model_weight_ensemble(members, weights): # 确定需要平均的层数 n_layers = len(members[0].get_weights()) # 创建一组平均模型权重 avg_model_weights = list() for layer in range(n_layers): # 从每个模型收集这一层 layer_weights = array([model.get_weights()[layer] for model in members]) # 此层的权重加权平均 avg_layer_weights = average(layer_weights, axis=0, weights=weights) # 存储平均层权重 avg_model_weights.append(avg_layer_weights) # 创建一个具有相同结构的全新模型 model = clone_model(members[0]) # 在新模型中设置权重 model.set_weights(avg_model_weights) model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy']) return model # 评估集成中的特定数量成员 def evaluate_n_members(members, n_members, testX, testy): # 选择成员子集 subset = members[:n_members] # 准备一个指数递减权重数组 alpha = 2.0 weights = [exp(-i/alpha) for i in range(1, n_members+1)] # 创建一个由所有模型权重加权平均而成的新模型 model = model_weight_ensemble(subset, weights) # 进行预测并评估准确率 _, test_acc = model.evaluate(testX, testy, verbose=0) return test_acc # 生成二维分类数据集 X, y = make_blobs(n_samples=1100, centers=3, n_features=2, cluster_std=2, random_state=2) # 独热编码输出变量 y = to_categorical(y) # 分割成训练集和测试集 n_train = 100 trainX, testX = X[:n_train, :], X[n_train:, :] trainy, testy = y[:n_train], y[n_train:] # 按顺序加载模型 members = load_all_models(490, 500) print('Loaded %d models' % len(members)) # 反转已加载的模型,以便我们先构建最后一个模型的集成 members = list(reversed(members)) # 在保留集上评估不同数量的集成 single_scores, ensemble_scores = list(), list() for i in range(1, len(members)+1): # 评估具有 i 个模型的集成 ensemble_score = evaluate_n_members(members, i, testX, testy) # 单独评估第 i 个模型 _, single_score = members[i-1].evaluate(testX, testy, verbose=0) # 总结这一步 print('> %d: single=%.3f, ensemble=%.3f' % (i, single_score, ensemble_score)) ensemble_scores.append(ensemble_score) single_scores.append(single_score) # 绘制分数与集成成员数量的关系 x_axis = [i for i in range(1, len(members)+1)] pyplot.plot(x_axis, single_scores, marker='o', linestyle='None') pyplot.plot(x_axis, ensemble_scores, marker='o') pyplot.show() |
注意:由于算法或评估程序的随机性,或者数值精度的差异,您的结果可能有所不同。请考虑运行示例几次并比较平均结果。
运行示例显示性能有小幅提升,与线性衰减加权平均已保存模型类似。
|
1 2 3 4 5 6 7 8 9 10 |
> 1: single=0.814, ensemble=0.814 > 2: single=0.814, ensemble=0.815 > 3: single=0.811, ensemble=0.814 > 4: single=0.805, ensemble=0.814 > 5: single=0.807, ensemble=0.813 > 6: single=0.805, ensemble=0.813 > 7: single=0.802, ensemble=0.813 > 8: single=0.805, ensemble=0.813 > 9: single=0.805, ensemble=0.813 > 10: single=0.810, ensemble=0.813 |
测试准确率分数的折线图显示,与线性或平均加权模型相比,使用指数衰减对性能的稳定作用更强。
单个模型测试性能(蓝色点)和具有指数衰减的模型权重集成测试性能(橙色线)的折线图
扩展
本节列出了一些您可能希望探索的扩展本教程的想法。
- 模型数量。评估更多模型将其权重贡献给最终模型的效应。
- 衰减率。评估使用不同衰减率对指数加权平均的测试性能的影响。
如果您探索了这些扩展中的任何一个,我很想知道。
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
书籍
- 第 8.7.3 节 Polyak 平均, Deep Learning, 2016。
论文
- 通过平均加速随机逼近, 1992.
- 从缓慢收敛的 Robbins-Monro 过程进行有效估计, 1988.
API
文章
总结
在本教程中,您了解了如何将多个不同模型的权重组合成一个模型来进行预测。
具体来说,你学到了:
- 神经网络训练的随机性和挑战性可能意味着优化过程不会收敛。
- 通过对训练过程中观察到的模型权重的平均值创建模型,可以获得更稳定、有时性能更好的解决方案。
- 如何开发由多个已保存模型中的模型参数等权重、线性加权和指数加权平均创建的最终模型。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。






谢谢 Jason 的文章!
我想了解一下,为什么这种权重平均比优化器中的自适应学习率更有效?实际上,两者应该是等效的。
你是指具有自适应学习率的一个模型与集成模型相比吗?
集成模型仍然可以减少方差,并且可能比单一解决方案有更高的技能。这 realmente 取决于问题的复杂性。
嗨,Jason,
有什么区别,或者哪种更有效?是平均权重到一个模型,还是平均多个模型的输出/分数?
另外,如果我训练了几个独立模型,我是否仍然应该平均权重?还是应该对模型进行集成?
谢谢!
也许可以尝试一下,并使用最有效的方法。
谢谢您,先生,
我想了解集成和过拟合,您能说些什么吗?
集成模型可以使过拟合更具挑战性,而不是相反。
我尝试使用 `model_weight_ensemble` 函数,遇到了以下错误:
“模型 sequential 的权重尚未创建。模型首次调用输入或使用 `input_shape` 调用
build()时会创建权重。” :-/听到这个消息很遗憾,也许这些提示会有帮助
https://machinelearning.org.cn/faq/single-faq/why-does-the-code-in-the-tutorial-not-work-for-me
我想非常感谢您写这篇文章。即使我的代码仍然出现错误,这个想法也很棒!
谢谢!
请检查您的库版本。
现在可以了,我没有给我的模型输入尺寸。是我的错 :)。再次感谢!
很高兴听到这个!
这是一个有趣的概述。然而,最终,集成结果比单个模型结果差很多。我让模型收敛然后保存模型,并重复几次,然后平均收敛模型的权重,而不是各个 epoch 的权重。这会造成什么问题吗?我也初始化了偏差,但我猜那不是问题。
如果您的方法在您的数据集上给您带来了良好的结果,并且没有将测试数据的知识泄露到训练中,那就去做吧!
你好,Jason。
我正在 Keras 中查找 Batch Normalisation 的输出。
我已经将我的问题发布到 Stackoverflow 上了
https://stackoverflow.com/questions/66832395/is-output-of-batch-normalization-in-keras-dependent-on-number-of-epochs
您能看一下吗?
这是我在这里回答的一个常见问题
https://machinelearning.org.cn/faq/single-faq/can-you-comment-on-my-stackoverflow-question
嗨 Jason
感谢分享集成建模的知识。您能否分享一下如何克隆子类模型(自定义模型)的链接或说明?
抱歉,我没有关于该主题的教程。