通常,预测建模任务的输入特征会以意想不到的、通常是非线性方式相互作用。
这些交互作用可以被学习算法识别和建模。另一种方法是工程化新特征,以揭示这些交互作用,并查看它们是否能提高模型性能。此外,像将输入变量提高到某个幂次这样的变换,有助于更好地揭示输入变量与目标变量之间重要关系。
这些特征称为交互特征和多项式特征,它们允许使用更简单的建模算法,因为解释输入变量及其关系的复杂性的一部分被推回到了数据准备阶段。有时这些特征可以提高建模性能,尽管代价是增加了数千甚至数百万个额外的输入变量。
在本教程中,您将了解如何使用多项式特征转换来对数值输入变量进行特征工程。
完成本教程后,您将了解:
- 某些机器学习算法更喜欢或在多项式输入特征上表现更好。
- 如何使用多项式特征转换来为预测建模创建输入变量的新版本。
- 多项式次数对转换创建的输入特征数量的影响。
立即开始您的项目,阅读我的新书《机器学习数据准备》,其中包含分步教程和所有示例的Python源代码文件。
让我们开始吧。

如何在机器学习中使用多项式特征变换
照片由D Coetzee拍摄,保留部分权利。
教程概述
本教程分为五个部分;它们是:
- 多项式特征
- 多项式特征转换
- 声纳数据集
- 多项式特征转换示例
- 多项式次数的影响
多项式特征
多项式特征是通过将现有特征提高到指数而创建的特征。
例如,如果一个数据集只有一个输入特征 X,那么多项式特征将是添加一个新特征(列),其值通过对 X 中的值进行平方计算,例如 X^2。这个过程可以对数据集中的每个输入变量重复进行,从而创建每个变量的转换版本。
因此,多项式特征是一种特征工程,例如基于现有特征创建新输入特征。
多项式的“次数”用于控制添加的特征数量,例如,次数为 3 将为每个输入变量添加两个新变量。通常使用较小的次数,例如 2 或 3。
总的来说,使用大于 3 或 4 的 d 是不寻常的,因为对于较大的 d 值,多项式曲线会变得非常灵活,并可能呈现出一些非常奇怪的形状。
— 第 266 页,《统计学习导论(附R应用)》,2014年。
添加表示特征之间交互作用的新变量也很常见,例如,一个表示一个变量乘以另一个变量的新列。这也可以为每个输入变量重复进行,为每对输入变量创建新的“交互”变量。
输入变量的平方或立方版本会改变概率分布,分离小值和大值,随着指数的增大,这种分离会增加。
这种分离可以帮助一些机器学习算法做出更好的预测,并且对于回归预测建模任务,以及通常具有数值输入变量的任务来说很常见。
通常,线性算法,如线性回归和逻辑回归,对使用多项式输入变量响应良好。
线性回归在模型参数上是线性的,并且向模型添加多项式项是让模型识别非线性模式的有效方法。
— 第 11 页,《特征工程与选择》,2019年。
例如,当用作线性回归算法的输入时,该方法更广泛地称为多项式回归。
多项式回归通过添加额外的预测变量来扩展线性模型,这些预测变量是通过将每个原始预测变量提高到某个幂次而获得的。例如,三次回归使用三个变量 X、X^2 和 X^3 作为预测变量。这种方法提供了一种对数据进行非线性拟合的简单方法。
— 第 265 页,《统计学习导论(附R应用)》,2014年。
想开始学习数据准备吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
多项式特征转换
scikit-learn Python机器学习库通过PolynomialFeatures类提供了多项式特征转换。
创建的特征包括
- 偏差(值为1.0)
- 每个次数的幂值(例如 x^1、x^2、x^3、…)
- 所有特征对的交互作用(例如 x1 * x2、x1 * x3、…)
例如,对于值为 2 和 3、次数为 2 的两个输入变量,创建的特征将是
- 1(偏差)
- 2^1 = 2
- 3^1 = 3
- 2^2 = 4
- 3^2 = 9
- 2 * 3 = 6
我们可以用一个例子来演示这一点
|
1 2 3 4 5 6 7 8 9 10 |
# 演示创建的特征类型 from numpy import asarray from sklearn.preprocessing import PolynomialFeatures # 定义数据集 data = asarray([[2,3],[2,3],[2,3]]) print(data) # 执行数据集的多项式特征转换 trans = PolynomialFeatures(degree=2) data = trans.fit_transform(data) print(data) |
运行示例首先报告原始数据,其中有两个特征(列),每个特征具有相同的值,即 2 或 3。
然后创建多项式特征,生成六个特征,与上面描述的一致。
|
1 2 3 4 5 6 7 |
[[2 3] [2 3] [2 3]] [[1. 2. 3. 4. 6. 9.] [1. 2. 3. 4. 6. 9.] [1. 2. 3. 4. 6. 9.]] |
“degree”参数控制创建的特征数量,默认为 2。
“interaction_only”参数意味着只包括原始值(次数 1)和交互作用(值对相乘),默认为*False*。
“include_bias”参数默认为*True*,表示包含偏差特征。
我们将更深入地研究如何在实际数据集中使用多项式特征转换。
首先,让我们介绍一个实际数据集。
声纳数据集
声纳数据集是用于二元分类的标准机器学习数据集。
它涉及 60 个实值输入和一个二类目标变量。数据集中有 208 个示例,并且类别相当平衡。
使用重复分层10折交叉验证,基线分类算法的分类准确率约为53.4%。在此数据集上的顶级性能约为88%,使用重复分层10折交叉验证。
数据集描述了岩石或模拟地雷的雷达回波。
您可以从这里了解更多关于数据集的信息
无需下载数据集;我们将从我们的示例中自动下载它。
首先,让我们加载并总结数据集。完整的示例列在下面。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# 加载并总结声纳数据集 from pandas import read_csv from pandas.plotting import scatter_matrix from matplotlib import pyplot # 加载数据集 url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/sonar.csv" dataset = read_csv(url, header=None) # 总结数据集的形状 print(dataset.shape) # 总结每个变量 print(dataset.describe()) # 变量的直方图 dataset.hist() pyplot.show() |
运行示例首先总结加载数据集的形状。
这证实了 60 个输入变量、一个输出变量和 208 行数据。
提供了输入变量的统计摘要,显示值是数值,大约在 0 到 1 之间。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
(208, 61) 0 1 2 ... 57 58 59 count 208.000000 208.000000 208.000000 ... 208.000000 208.000000 208.000000 mean 0.029164 0.038437 0.043832 ... 0.007949 0.007941 0.006507 std 0.022991 0.032960 0.038428 ... 0.006470 0.006181 0.005031 min 0.001500 0.000600 0.001500 ... 0.000300 0.000100 0.000600 25% 0.013350 0.016450 0.018950 ... 0.003600 0.003675 0.003100 50% 0.022800 0.030800 0.034300 ... 0.005800 0.006400 0.005300 75% 0.035550 0.047950 0.057950 ... 0.010350 0.010325 0.008525 max 0.137100 0.233900 0.305900 ... 0.044000 0.036400 0.043900 [8 rows x 60 columns] |
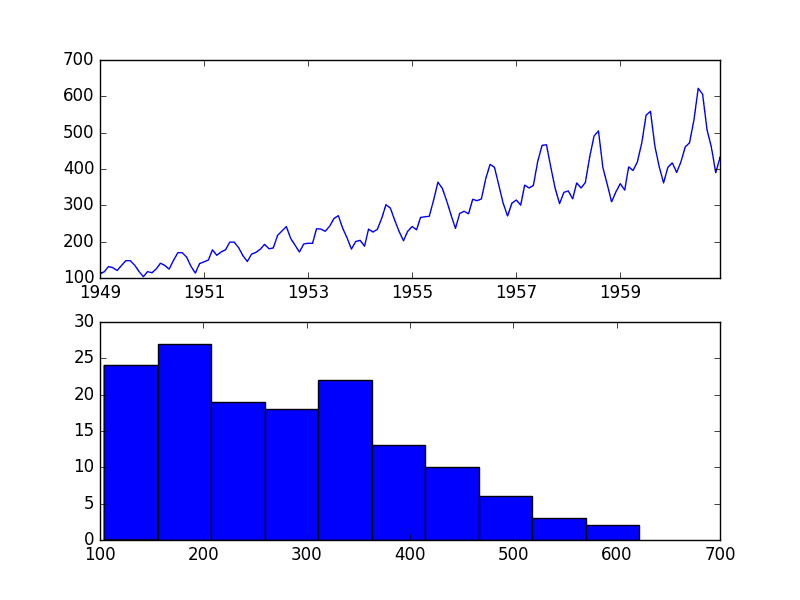
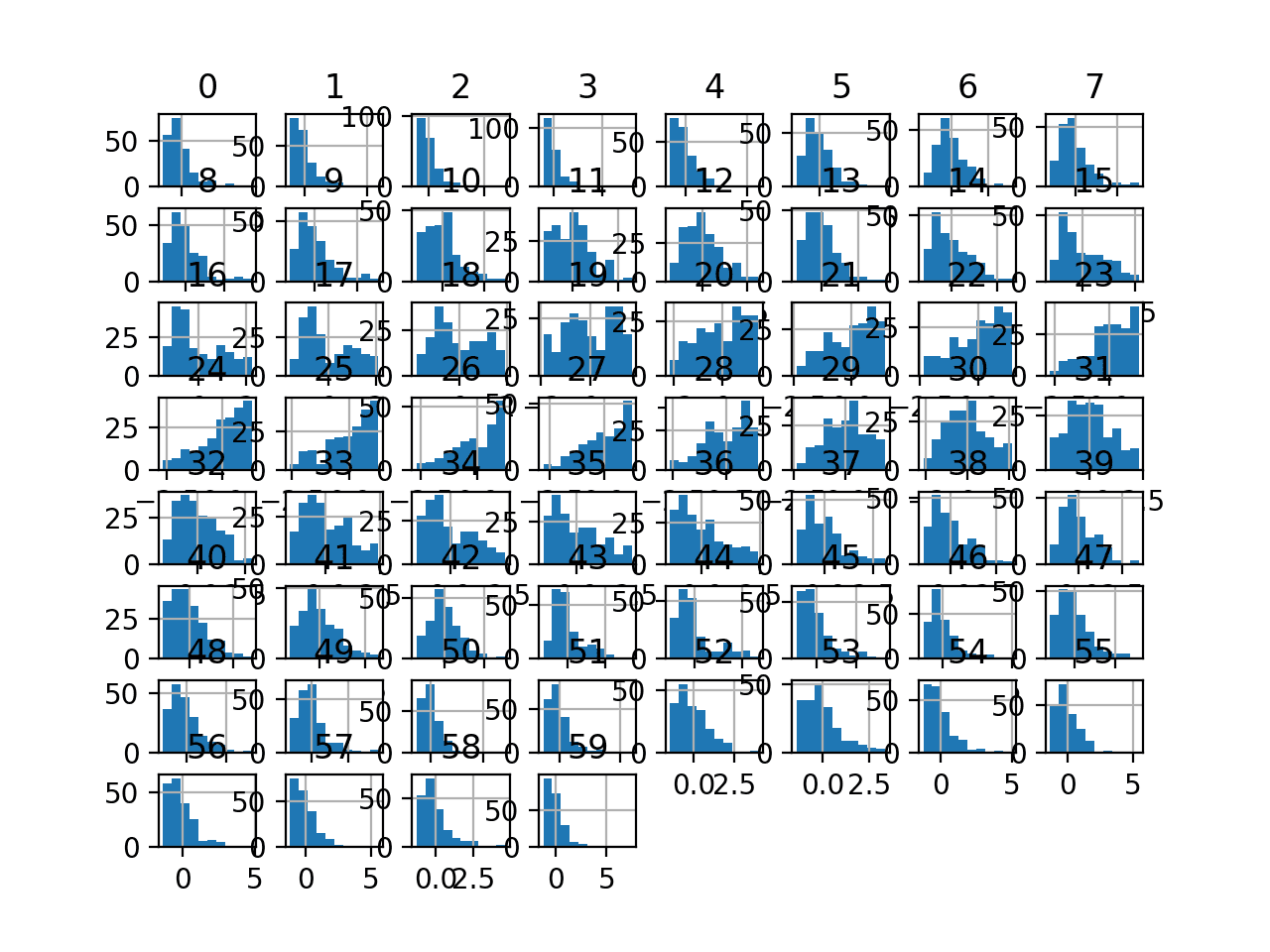
最后,为每个输入变量创建了一个直方图。
如果我们忽略图表的杂乱,只关注直方图本身,我们可以看到许多变量具有偏斜分布。
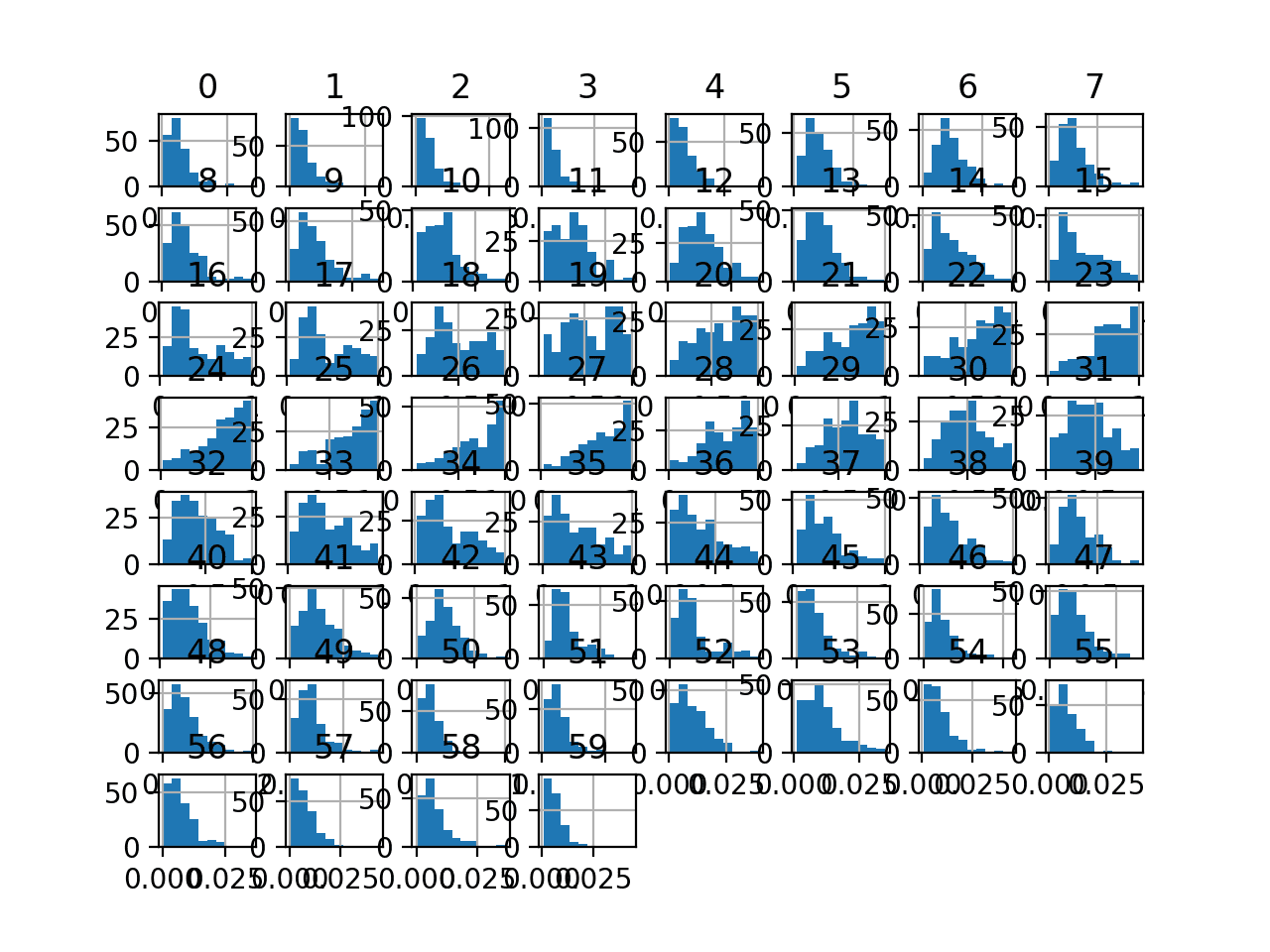
声纳二元分类数据集输入变量的直方图图
接下来,让我们在原始数据集上拟合和评估一个机器学习模型。
我们将使用具有默认超参数的k近邻算法,并通过重复分层k折交叉验证进行评估。完整的示例列在下面。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
# 在原始声纳数据集上评估 knn from numpy import mean from numpy import std from pandas import read_csv from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.neighbors import KNeighborsClassifier from sklearn.preprocessing import LabelEncoder from matplotlib import pyplot # 加载数据集 url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/sonar.csv" dataset = read_csv(url, header=None) data = dataset.values # 分割为输入和输出列 X, y = data[:, :-1], data[:, -1] # 确保输入是浮点数,输出是整数标签 X = X.astype('float32') y = LabelEncoder().fit_transform(y.astype('str')) # 定义和配置模型 model = KNeighborsClassifier() # 评估模型 cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) n_scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1, error_score='raise') # 报告模型性能 print('Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores))) |
运行示例评估 KNN 模型在原始声纳数据集上的性能。
注意:由于算法或评估过程的随机性,或数值精度的差异,您的结果可能有所不同。考虑多次运行示例并比较平均结果。
我们可以看到,该模型实现了大约 79.7% 的平均分类准确率,这表明它具有技能(优于 53.4%),并且接近良好性能(88%)。
|
1 |
准确率:0.797 (0.073) |
接下来,让我们探讨对数据集进行多项式特征转换。
多项式特征转换示例
我们可以直接将多项式特征转换应用于 Sonar 数据集。
在这种情况下,我们将使用次数 3。
|
1 2 3 4 |
... # 执行数据集的多项式特征转换 trans = PolynomialFeatures(degree=3) data = trans.fit_transform(data) |
让我们在声纳数据集上尝试一下。
创建 Sonar 数据集的特征转换并总结创建的特征的完整示例如下。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
# 可视化 Sonar 数据集的多项式特征转换 from pandas import read_csv from pandas import DataFrame from pandas.plotting import scatter_matrix from sklearn.preprocessing import PolynomialFeatures from matplotlib import pyplot # 加载数据集 url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/sonar.csv" dataset = read_csv(url, header=None) # 仅检索数字输入值 data = dataset.values[:, :-1] # 执行数据集的多项式特征转换 trans = PolynomialFeatures(degree=3) data = trans.fit_transform(data) # 将数组转换回数据框 dataset = DataFrame(data) # 总结 print(dataset.shape) |
运行示例会对 Sonar 数据集执行多项式特征转换。
我们可以看到,对于原始数据集,我们的特征从 61 个(60 个输入特征)增加到 39,711 个特征(39,710 个输入特征)。
|
1 |
(208, 39711) |
接下来,让我们评估与上一节相同的 KNN 模型,但这次是在数据集的多项式特征转换上。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
# 使用多项式特征转换评估 Sonar 数据集上的 KNN from numpy import mean from numpy import std from pandas import read_csv from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.neighbors import KNeighborsClassifier from sklearn.preprocessing import LabelEncoder from sklearn.preprocessing import PolynomialFeatures from sklearn.pipeline import Pipeline from matplotlib import pyplot # 加载数据集 url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/sonar.csv" dataset = read_csv(url, header=None) data = dataset.values # 分割为输入和输出列 X, y = data[:, :-1], data[:, -1] # 确保输入是浮点数,输出是整数标签 X = X.astype('float32') y = LabelEncoder().fit_transform(y.astype('str')) # 定义管道 trans = PolynomialFeatures(degree=3) model = KNeighborsClassifier() pipeline = Pipeline(steps=[('t', trans), ('m', model)]) # 评估管道 cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) n_scores = cross_val_score(pipeline, X, y, scoring='accuracy', cv=cv, n_jobs=-1, error_score='raise') # 报告管道性能 print('Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores))) |
注意:由于算法或评估过程的随机性,或数值精度的差异,您的结果可能有所不同。考虑多次运行示例并比较平均结果。
运行示例,我们可以看到多项式特征转换将性能从无转换时的 79.7% 准确率提升到有转换时的约 80.0% 准确率。
|
1 |
准确率:0.800 (0.077) |
接下来,让我们探讨不同缩放范围的效果。
多项式次数的影响
多项式的次数会急剧增加输入特征的数量。
为了了解这对特征数量的影响有多大,我们可以使用一系列不同的次数进行转换,并比较数据集中特征的数量。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
# 比较次数对创建特征数量的影响 from pandas import read_csv from sklearn.preprocessing import LabelEncoder from sklearn.preprocessing import PolynomialFeatures from matplotlib import pyplot # 获取数据集 定义 获取_数据集(): # 加载数据集 url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/sonar.csv" dataset = read_csv(url, header=None) data = dataset.values # 分离输入和输出列 X, y = data[:, :-1], data[:, -1] # 确保输入为浮点数,输出为整数标签 X = X.astype('float32') y = LabelEncoder().fit_transform(y.astype('str')) 返回 X, y # 定义数据集 X, y = get_dataset() # 计算特征数量的变化 num_features = list() degress = [i for i in range(1, 6)] for d in degress: # 创建转换器 trans = PolynomialFeatures(degree=d) # 拟合和转换 data = trans.fit_transform(X) # 记录特征数量 num_features.append(data.shape[1]) # 总结 print('Degree: %d, Features: %d' % (d, data.shape[1])) # 绘制次数与创建的特征数量的关系图 pyplot.plot(degress, num_features) pyplot.show() |
运行示例首先报告了从 1 到 5 的次数以及数据中的特征数量。
我们可以看到,次数为 1 没有效果,并且特征数量从 2 到 5 急剧增加。
这表明,对于非常小的数据集以外的情况,应使用次数 2 或 3 来避免输入变量的急剧增加。
|
1 2 3 4 5 |
次数:1,特征:61 次数:2,特征:1891 次数:3,特征:39711 次数:4,特征:635376 次数:5,特征:8259888 |
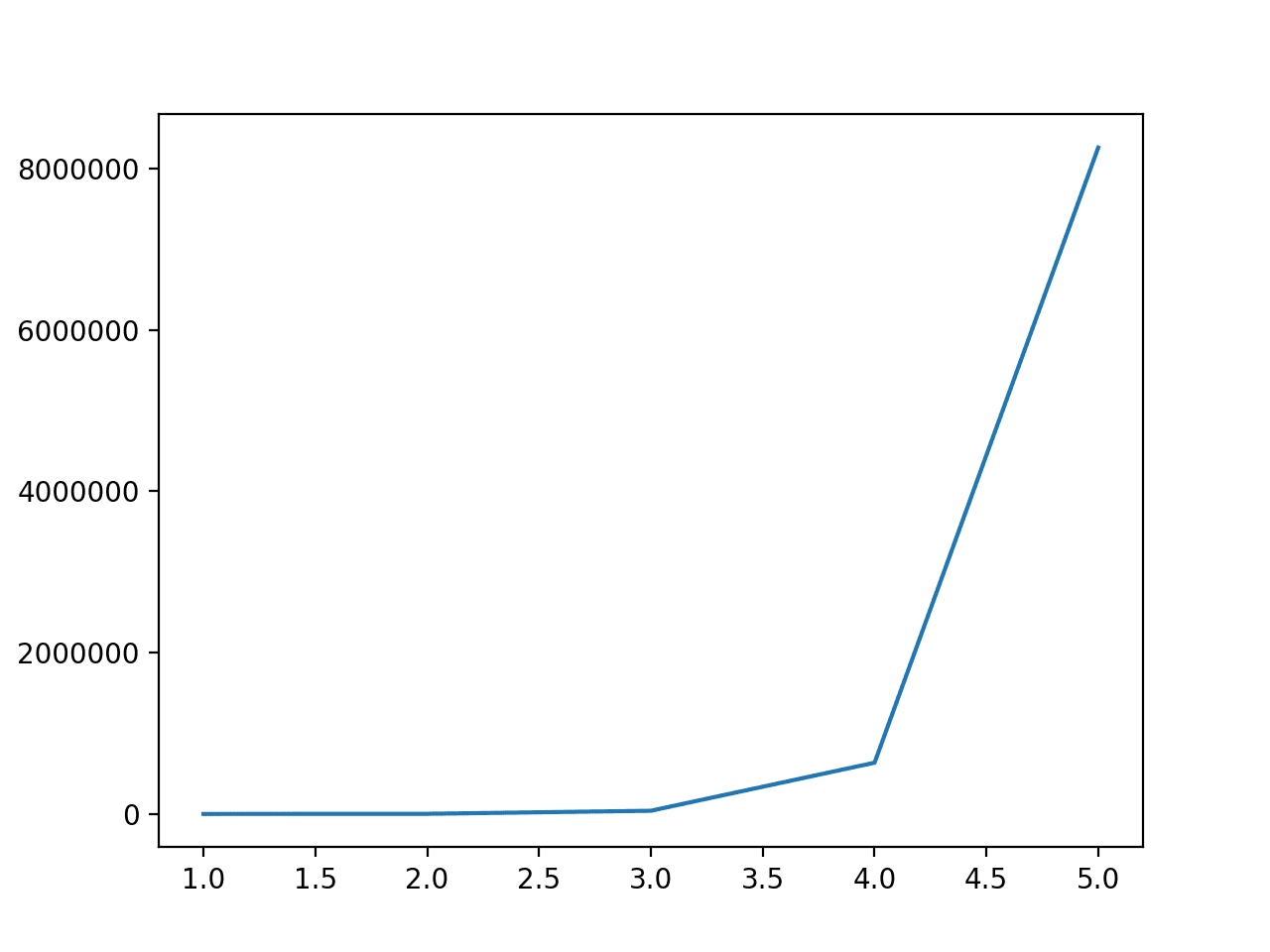
多项式特征转换的次数与输入特征数量的关系图
更多的特征可能会导致过拟合,从而导致结果变差。
将多项式特征转换的次数视为超参数并为您的数据集测试不同的值可能是一个好主意。
下面的示例探讨了次数从 1 到 4 的值,并评估了它们对所选模型分类准确率的影响。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 |
# 探索次数对多项式特征转换准确率的影响 from numpy import mean from numpy import std from pandas import read_csv from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.neighbors import KNeighborsClassifier from sklearn.preprocessing import PolynomialFeatures from sklearn.preprocessing import LabelEncoder from sklearn.pipeline import Pipeline from matplotlib import pyplot # 获取数据集 定义 获取_数据集(): # 加载数据集 url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/sonar.csv" dataset = read_csv(url, header=None) data = dataset.values # 分离输入和输出列 X, y = data[:, :-1], data[:, -1] # 确保输入为浮点数,输出为整数标签 X = X.astype('float32') y = LabelEncoder().fit_transform(y.astype('str')) 返回 X, y # 获取要评估的模型列表 定义 获取_模型(): models = dict() for d in range(1,5): # 定义管道 trans = PolynomialFeatures(degree=d) model = KNeighborsClassifier() models[str(d)] = Pipeline(steps=[('t', trans), ('m', model)]) 返回 模型 # 使用交叉验证评估给定模型 def evaluate_model(model, X, y): cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1, error_score='raise') 返回 分数 # 定义数据集 X, y = get_dataset() # 获取要评估的模型 模型 = 获取_模型() # 评估模型并存储结果 results, names = list(), list() for name, model in models.items(): scores = evaluate_model(model, X, y) results.append(scores) names.append(name) print('>%s %.3f (%.3f)' % (name, mean(scores), std(scores))) # 绘制模型性能以供比较 pyplot.boxplot(results, labels=names, showmeans=True) pyplot.show() |
运行示例会为每个多项式次数报告平均分类准确率。
注意:由于算法或评估过程的随机性,或数值精度的差异,您的结果可能有所不同。考虑多次运行示例并比较平均结果。
在这种情况下,我们可以看到,除了次数为 3 的情况外,性能通常比没有转换(次数 1)的情况要差。
在进行转换之前或之后对数据进行缩放,以了解其对模型性能的影响,这可能很有趣。
|
1 2 3 4 |
>1 0.797 (0.073) >2 0.793 (0.085) >3 0.800 (0.077) >4 0.795 (0.079) |
创建箱线图以总结每个多项式次数的分类准确率得分。
我们可以看到性能基本保持平稳,在次数为 4 时可能出现过拟合的早期迹象。
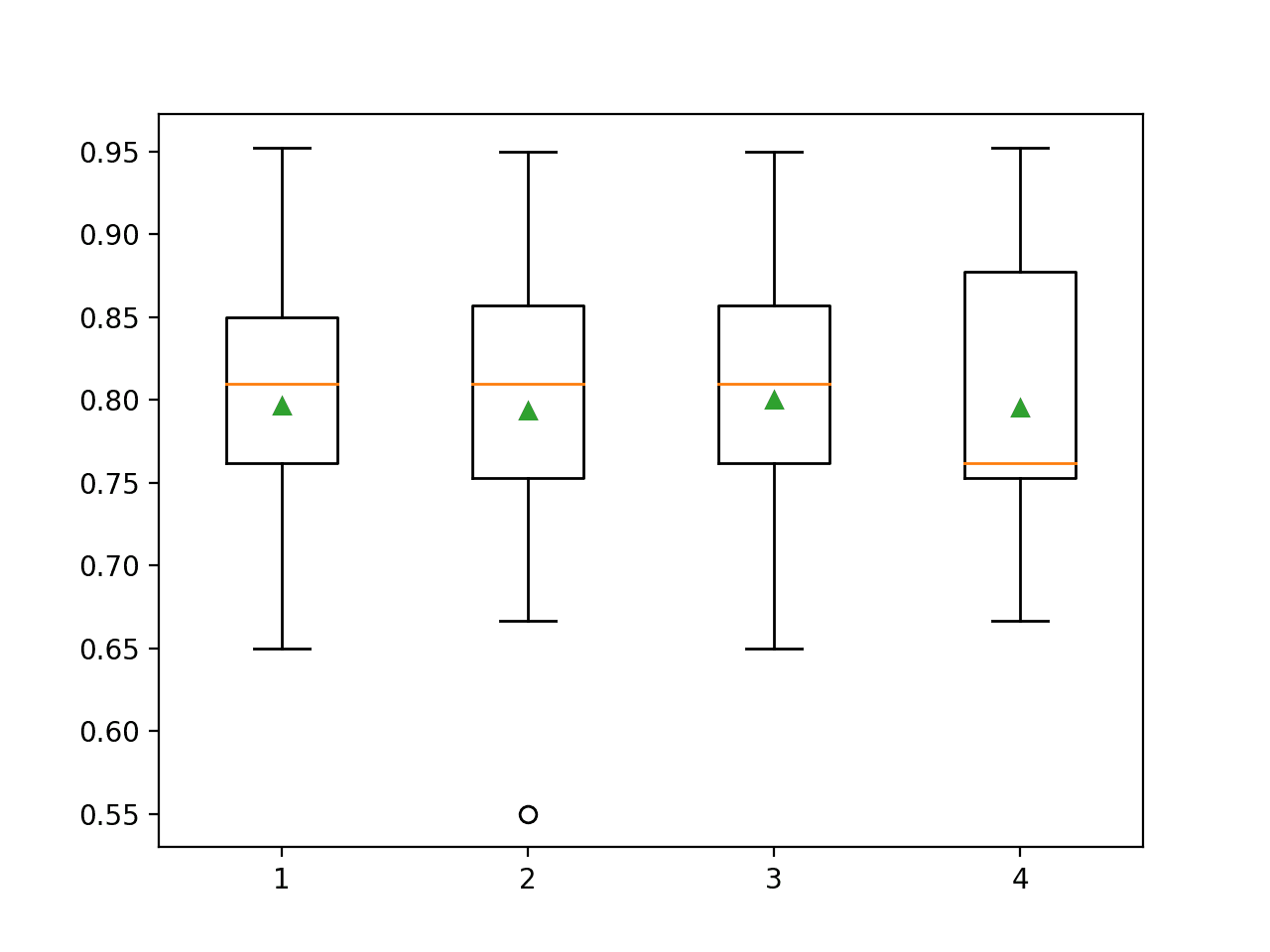
KNN 在 Sonar 数据集上进行多项式特征转换的分类准确率的次数箱线图
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
书籍
- 统计学习导论:R语言应用, 2014.
- 特征工程与选择, 2019.
API
文章
总结
在本教程中,您了解了如何使用多项式特征转换来对数值输入变量进行特征工程。
具体来说,你学到了:
- 某些机器学习算法更喜欢或在多项式输入特征上表现更好。
- 如何使用多项式特征转换来为预测建模创建输入变量的新版本。
- 多项式次数对转换创建的输入特征数量的影响。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。




你好,又见面了:)
我将使用前馈神经网络作为回归器,使用(5个输入特征/传感器读数)。
我想为这个项目尝试多项式特征转换以创建更多输入特征
我的问题是
我可以在执行 PolynomialFeatures 后执行(RobustScaler)或(StandardScaler)吗?
非常感谢
是的。
一种方法是将转换作为管道的一部分应用于您的数据集,然后将数据提供给模型。
这个案例研究对于多项式模型的优势并没有说服力。
您最初有 200 个数据点和 60 个变量。添加 1000 多个变量后,您的模型准确率提高了 0.3%。
1:这种程度的提高可能只是偶然发生的,即仅仅重新训练原始模型。
2:没有保留集 cv。实际上,您将有 150 个观测值用于建模,并且大多数模型在没有特征选择的情况下都会过拟合。
3:它很好地演示了 Python 模块的 OO 性质对于统计工作流程来说是多么麻烦。在 R 中,使用一半的代码量和两倍的可读性就可以做到同样的事情。
是的,我可以做得更好。感谢您的反馈。
你好 Jason,
是否可以使用 Keras 进行多项式回归?
您有简单的例子吗?
谢谢
Marco
是的,您可以生成特征,然后将它们传递给您的 keras 模型。
没有,我没有例子,但它应该很简单。
感谢您的分享,
如果我们想做预测,是否也应该为测试数据实现多项式特征转换?
再次感谢
是的,必须对训练集和测试集使用相同的转换对象。例如,它是在训练集上拟合的,然后应用于训练集和测试集。
你好 Jason,
您的博客文章对像我这样的从业者来说非常有趣!这次我有一个问题:多项式特征转换是否不会引入多重共线性(例如 x 和 x^2 之间的相关性),从而可能导致模型性能下降?
非常感谢
谢谢。
它可能会,这会影响一些线性模型。
尊敬的Jason博士,
我必须说,我没有理解 PolynomialFeatures 转换产生的模式。
我使用交互项和多项式以及仅交互项,使用数组 [1,2,3,4] 进行了以下操作
在 https://stackoverflow.com/questions/51906274/cannot-understand-with-sklearns-polynomialfeatures 的第二个答案的帮助下,您会得到以下模式。
那么 fit_transform(data) 会生成形式
如果您排除 a^2, b^2, c^2 和 d^2 的平方。
其类型是
度为 3 且值为 2 的情况,例如 data = [a,b]
转换后的输出数量 = (n + d)!/(n! * d!) 其中 n = 数字的数量,d = 多项式的次数。
例如,数字数量 = 3,多项式次数 = 2,
转换后的输出数量 = (n + d)! / (n! * d!) = 5!/(3! * 2!) =10
例如,数字数量 = 2,多项式次数 = 3
转换后的输出数量 = 5!/(2!*3!) = 10
谢谢你,
悉尼的Anthony
感谢分享您的发现。
尊敬的Jason博士,
我一直在尝试标题为“Polynomial Feature Transform Example”的代码,该代码也包含在您的书的第 310 页(第 327 页,共 398 页)的列表 23.10 中。
特别相关的几行是
我问这个问题“,,,作者为什么没有通过
并将其输入到 cross_val_score 中?
请注意,我没有使用管道,而是使用了转换后的多项式特征 X2。
我仍然得到了相同的结果。
问题是:在原始代码中,管道似乎执行了度为 3 的 PolynomialFeatures 函数,而没有将转换后的 (X) = X2 放入 cross_val_score 函数。
换句话说,在原始代码中,该管道是如何在不使用转换后的特征的情况下计算转换后的特征,并且仍然得到相同的结果的?
谢谢你,
悉尼的Anthony
管道将转换应用于输入数据,然后将转换后的数据传递给模型。
您可以在这里了解更多关于管道工作原理的信息
https://scikit-learn.cn/stable/modules/generated/sklearn.pipeline.Pipeline.html
尊敬的Jason博士,
“管道将转换应用于输入数据,然后将转换后的数据传递给模型。”
问题已澄清
谢谢你。
悉尼的安东尼。
很高兴听到这个消息。
嗨,Jason,
感谢您的文章,它非常翔实。我的问题是关于这项技术的应用。应该将特征转换为多项式用于回归问题,还是也可以用于分类问题?
谢谢你,
Bill
多项式特征可以帮助回归和分类任务,可以尝试与没有多项式特征的相同模型进行比较。
嗨,Jason,
我有一个问题。在 Pipeline 中,StandardScale 和 Polynomial Features 的正确顺序是什么?还是 Polynomial Features 和 StandardScale?我对这个感到困惑。
我的建议是测试一下它是否会产生影响。
我的直觉是,在这种情况下,它可能无关紧要。
明白了!非常感谢!您的网站太棒了!
不客气。
谢谢!
嗨,我只有一个自变量,它与目标变量之间存在非线性关系,我是否应该为基于树的模型从该自变量创建多项式特征?
也许可以尝试一下,并与其他方法的结果进行比较。
我创建了高达 4 次的多项式特征,它们显着提高了我的线性回归模型的 R2 分数(经交叉验证验证)。但是我的问题是,新创建的多项式特征与它们生成的原始特征高度相关,皮尔逊相关系数高于 0.80。这是否会导致多重共线性问题?或者模型结果是可以接受的?
有可能性。
专注于模型性能。如果模型表现更好,则保留新特征。
Jason 先生,非常感谢您的建议。我还有另一个问题。您提到过一本书的参考资料说“对于 d(次数)的大值,多项式曲线会变得过于灵活,并可能呈现非常奇怪的形状”。我的问题是,对于 d 的大值,例如 5,如果线性模型性能在提高,并且我看不到回归线有任何异常,我们可以保留这些特征来构建模型吗?
实际上,在我的案例中,我有 13 个特征,我找到了最重要的特征,从那个最重要的特征创建了 5 次多项式特征,观察到模型性能在 d=5 时有显着提高,在 d=6 时开始下降。我希望您能理解我的问题。提前感谢。
当然,使用最适合您数据和测试的方法。确保您的测试方法足够健壮,这样您就不会欺骗自己。
非常感谢您的回复。我非常欣赏您写的精彩文章。
谢谢。
嗨 Jason,我有一个问题。如果我创建了一个 VIF=5.6、p 值=0.7 的多项式特征,它将 Adj. R2 提高了 2.5%。我该如何解释这样的特征?
请谢谢。
抱歉,我尽量避免为读者解释结果。
可以尝试与使用其他方法的结果进行比较,并根据您的具体应用选择最有效或最可靠的方法。
感谢您的快速回复。我非常感激。您的评论对像我这样的学习者很有价值。
不客气。
您的文章非常精彩,内容翔实,解释和示例丰富。您是绝地大师!😀
谢谢!
输入变量为 2,3,4 且次数为 2 的情况下,输出变量的顺序是什么?
可能是这个?
1(偏差)
2^1
3^1
4^1
2^2
3^2
4^2
2*3
3*4
尝试替换
data = asarray([[2,3,4],[2,3,4]])
您会看到它是
1, 2^1, 3^1, 4^1, 2^2, 2*3, 2*4, 3^2, 3*4, 4^2
但 Jason Brownlee 在上面写道
“例如,有两个输入变量,值为 2 和 3,次数为 2,创建的特征将是
1(偏差)
2^1 = 2
3^1 = 3
2^2 = 4
3^2 = 9
2 * 3 = 6”
所以,交互项似乎是最后的。
您查看代码的输出,而不是要点,您会看到它是顺序为 [2,3,4,6,9] 而不是。
我通过多项式次数=2 生成了新特征,现在我应该替换/丢弃原始特征,还是保留所有特征及其多项式特征用于回归?
嗨 Salaf…以下内容可能对您理解一般数据集转换有所帮助
https://machinelearning.org.cn/how-to-improve-neural-network-stability-and-modeling-performance-with-data-scaling/