线性回归和高斯朴素贝叶斯等机器学习算法假设数值变量服从高斯概率分布。
您的数据可能不服从高斯分布,而是服从类高斯分布(例如,接近高斯分布但存在异常值或偏斜)或完全不同的分布(例如,指数分布)。
因此,通过将输入和/或输出变量转换为高斯分布或更接近高斯分布,您可以在各种机器学习算法上获得更好的性能。Box-Cox 变换和 Yeo-Johnson 变换等幂变换提供了一种自动对数据执行这些变换的方法,并已在 scikit-learn Python 机器学习库中提供。
在本教程中,您将学习如何在 scikit-learn 中使用幂变换,使变量更接近高斯分布以便进行建模。
完成本教程后,您将了解:
- 许多机器学习算法在数值变量服从高斯概率分布时表现更佳。
- 幂变换是一种将数值输入或输出变量转换为高斯分布或更接近高斯概率分布的技术。
- 如何在 scikit-learn 中使用 PowerTransform 来使用 Box-Cox 和 Yeo-Johnson 变换来为预测建模准备数据。
通过我的新书《机器学习数据准备》来启动您的项目,包括分步教程和所有示例的 Python 源代码文件。
让我们开始吧。

如何使用 Scikit-learn 进行幂变换
图片由 Ian D. Keating 拍摄,保留部分权利。
教程概述
本教程分为五个部分;它们是:
- 使数据更接近高斯分布
- 幂变换
- 声纳数据集
- Box-Cox 变换
- Yeo-Johnson 变换
使数据更接近高斯分布
当变量分布为高斯分布时,许多机器学习算法表现更好。
回想一下,每个变量的观测值可以被认为是来自一个概率分布。高斯分布是一种常见的、具有熟悉钟形曲线的分布。它非常常见,以至于通常被称为“正态”分布。
有关高斯概率分布的更多信息,请参阅教程
某些算法(如线性回归和逻辑回归)明确假设实值变量服从高斯分布。其他非线性算法可能没有这个假设,但当变量服从高斯分布时,通常表现更好。
这适用于分类和回归任务中的实值输入变量,以及回归任务中的实值目标变量。
有一些数据准备技术可以用于转换每个变量,使其分布为高斯分布,或者如果不是高斯分布,则更接近高斯分布。
这些变换在数据分布最初接近高斯分布且受到偏斜或异常值影响时最有效。
变换的另一个常见原因是消除分布偏斜。非偏斜分布是大致对称的。这意味着落在分布均值任一侧的概率大致相等。
— 第 31 页,《应用预测建模》,2013 年。
幂变换是指使用幂函数(如对数或指数)使变量的概率分布呈高斯分布或更接近高斯分布的一类技术。
有关使变量高斯化的更多信息,请参阅教程
想开始学习数据准备吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
幂变换
幂变换将使变量的概率分布更接近高斯分布。
这通常被描述为消除分布中的偏斜,尽管更普遍地被描述为稳定分布的方差。
对数变换是称为幂变换的变换族中的一个特定示例。在统计学中,这些是方差稳定变换。
— 第 23 页,《机器学习的特征工程》,2018 年。
我们可以直接通过计算变量的对数或平方根来应用幂变换,尽管这可能不是给定变量的最佳幂变换。
用对数、平方根或倒数替换数据可能有助于消除偏斜。
— 第 31 页,《应用预测建模》,2013 年。
相反,我们可以使用变换的广义版本,它找到一个参数(lambda),该参数能最佳地将变量变换为高斯概率分布。
有两种流行的方法可以进行这种自动幂变换;它们是
- Box-Cox 变换
- Yeo-Johnson 变换
然后,转换后的训练数据集可以输入到机器学习模型中,以学习预测建模任务。
一个超参数,通常称为 lambda,用于控制变换的性质。
... 统计方法可用于经验性地确定合适的变换。Box 和 Cox(1964)提出了一系列由参数(表示为 lambda)索引的变换
— 第 32 页,《应用预测建模》,2013 年。
以下是 lambda 的一些常见值
- lambda = -1. 是倒数变换。
- lambda = -0.5 是倒数平方根变换。
- lambda = 0.0 是对数变换。
- lambda = 0.5 是平方根变换。
- lambda = 1.0 不进行变换。
用于每个变量变换的最佳超参数值可以存储并重新用于将来以相同方式转换新数据,例如测试数据集或未来的新数据。
这些幂变换可通过 scikit-learn Python 机器学习库中的 PowerTransformer 类获得。
该类接受一个名为“method”的参数,可以设置为“yeo-johnson”或“box-cox”以选择首选方法。它还会在变换后自动标准化数据,这意味着每个变量将具有零均值和单位方差。这可以通过将“standardize”参数设置为 False 来关闭。
我们可以通过一个简单的工作示例来演示 PowerTransformer。我们可以生成一个随机高斯数的样本,并通过计算指数对分布施加偏斜。然后可以使用 PowerTransformer 自动从数据中去除偏斜。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
# 对有偏斜的数据进行幂变换的演示 from numpy import exp from numpy.random import randn from sklearn.preprocessing import PowerTransformer from matplotlib import pyplot # 生成高斯数据样本 data = randn(1000) # 给数据分布增加偏斜 data = exp(data) # 带有偏斜的原始数据直方图 pyplot.hist(data, bins=25) pyplot.show() # 将数据重塑为行和列 data = data.reshape((len(data),1)) # 对原始数据进行幂变换 power = PowerTransformer(method='yeo-johnson', standardize=True) data_trans = power.fit_transform(data) # 变换后数据的直方图 pyplot.hist(data_trans, bins=25) pyplot.show() |
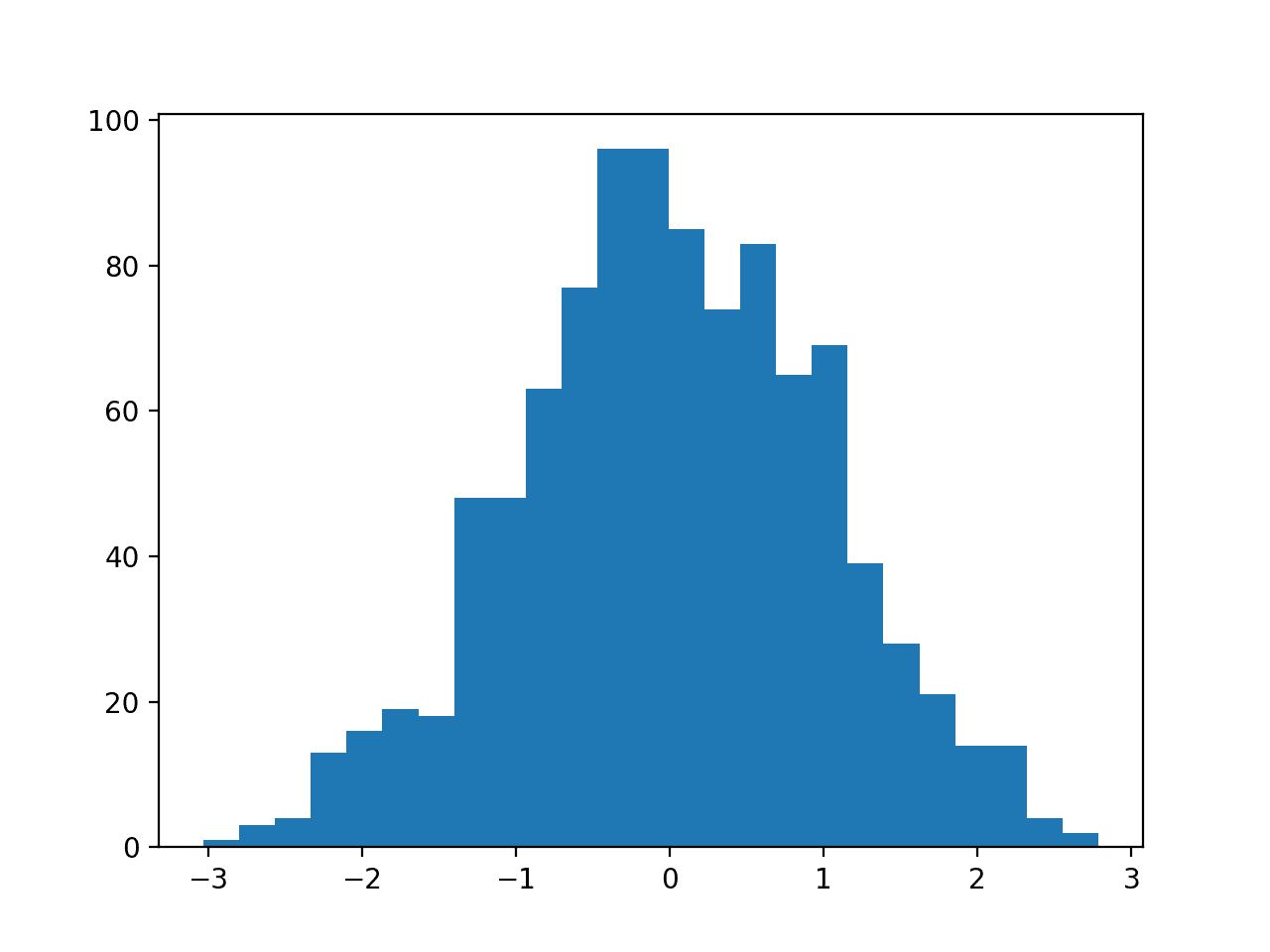
运行示例首先创建 1,000 个随机高斯值的样本,并向数据集添加偏斜。
从偏斜数据集中创建了一个直方图,清晰地显示分布被推到最左侧。
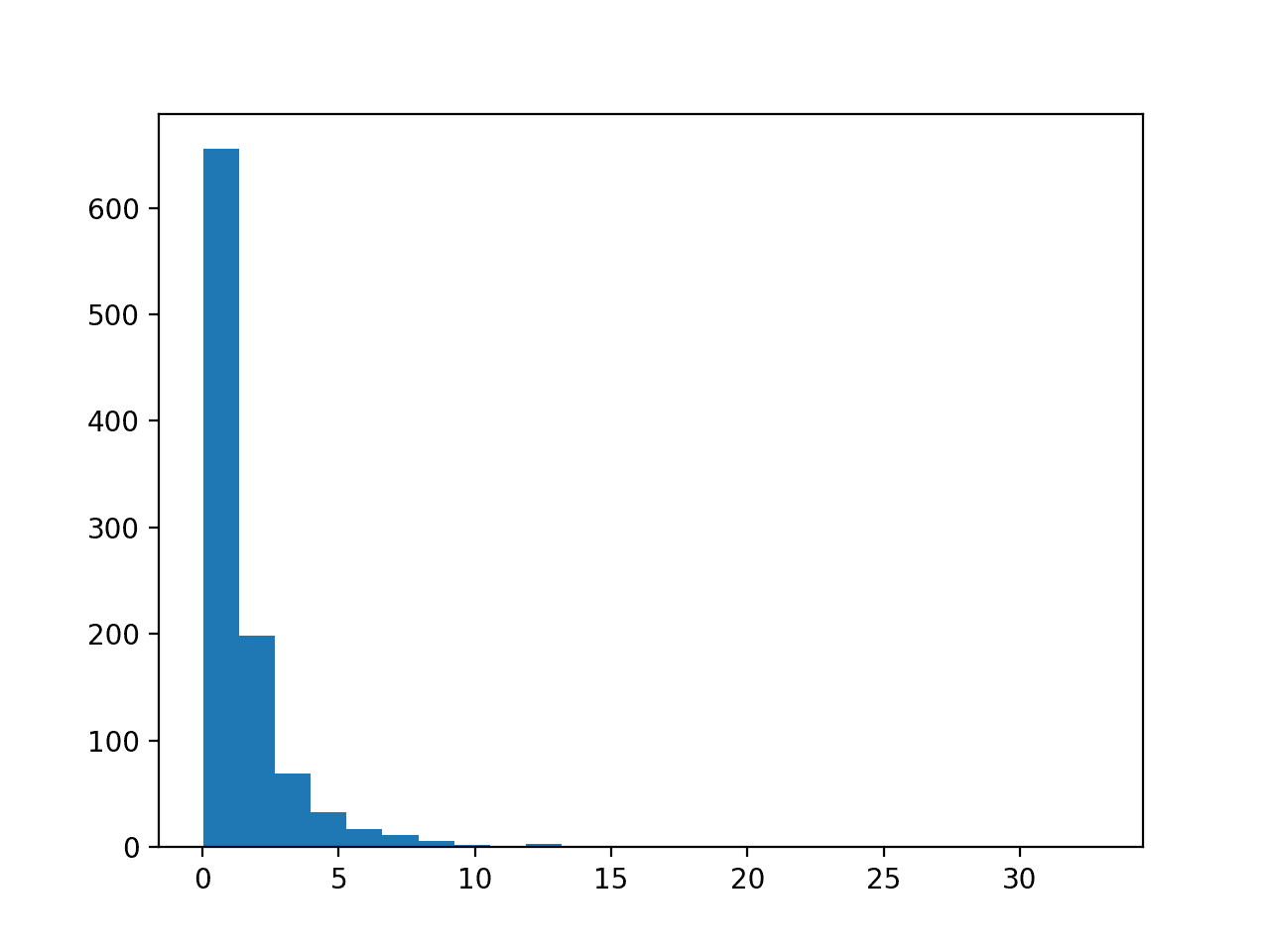
偏斜高斯分布的直方图
然后使用 PowerTransformer 使数据分布更接近高斯分布并标准化结果,将值集中在均值 0 和标准差 1.0 上。
创建了转换数据的直方图,显示了更接近高斯形状的数据分布。

幂变换后偏斜高斯数据的直方图
在接下来的部分中,我们将仔细研究如何在真实数据集上使用这两种幂变换。
接下来,我们介绍数据集。
声纳数据集
声纳数据集是用于二元分类的标准机器学习数据集。
它包含 60 个实值输入和一个 2 类目标变量。数据集中有 208 个示例,并且类是合理平衡的。
使用重复分层 10 折交叉验证,基线分类算法可以达到约 53.4% 的分类准确率。使用重复分层 10 折交叉验证,该数据集的最高性能约为 88%。
数据集描述了岩石或模拟地雷的雷达回波。
您可以从这里了解更多关于数据集的信息
无需下载数据集;我们将从我们的示例中自动下载它。
首先,让我们加载并总结数据集。完整的示例列在下面。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# 加载并总结声纳数据集 from pandas import read_csv from pandas.plotting import scatter_matrix from matplotlib import pyplot # 加载数据集 url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/sonar.csv" dataset = read_csv(url, header=None) # 总结数据集的形状 print(dataset.shape) # 总结每个变量 print(dataset.describe()) # 变量的直方图 dataset.hist() pyplot.show() |
运行示例首先总结加载数据集的形状。
这证实了 60 个输入变量、一个输出变量和 208 行数据。
提供了输入变量的统计摘要,显示值是数值,大约在 0 到 1 之间。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
(208, 61) 0 1 2 ... 57 58 59 count 208.000000 208.000000 208.000000 ... 208.000000 208.000000 208.000000 mean 0.029164 0.038437 0.043832 ... 0.007949 0.007941 0.006507 std 0.022991 0.032960 0.038428 ... 0.006470 0.006181 0.005031 min 0.001500 0.000600 0.001500 ... 0.000300 0.000100 0.000600 25% 0.013350 0.016450 0.018950 ... 0.003600 0.003675 0.003100 50% 0.022800 0.030800 0.034300 ... 0.005800 0.006400 0.005300 75% 0.035550 0.047950 0.057950 ... 0.010350 0.010325 0.008525 max 0.137100 0.233900 0.305900 ... 0.044000 0.036400 0.043900 [8 rows x 60 columns] |
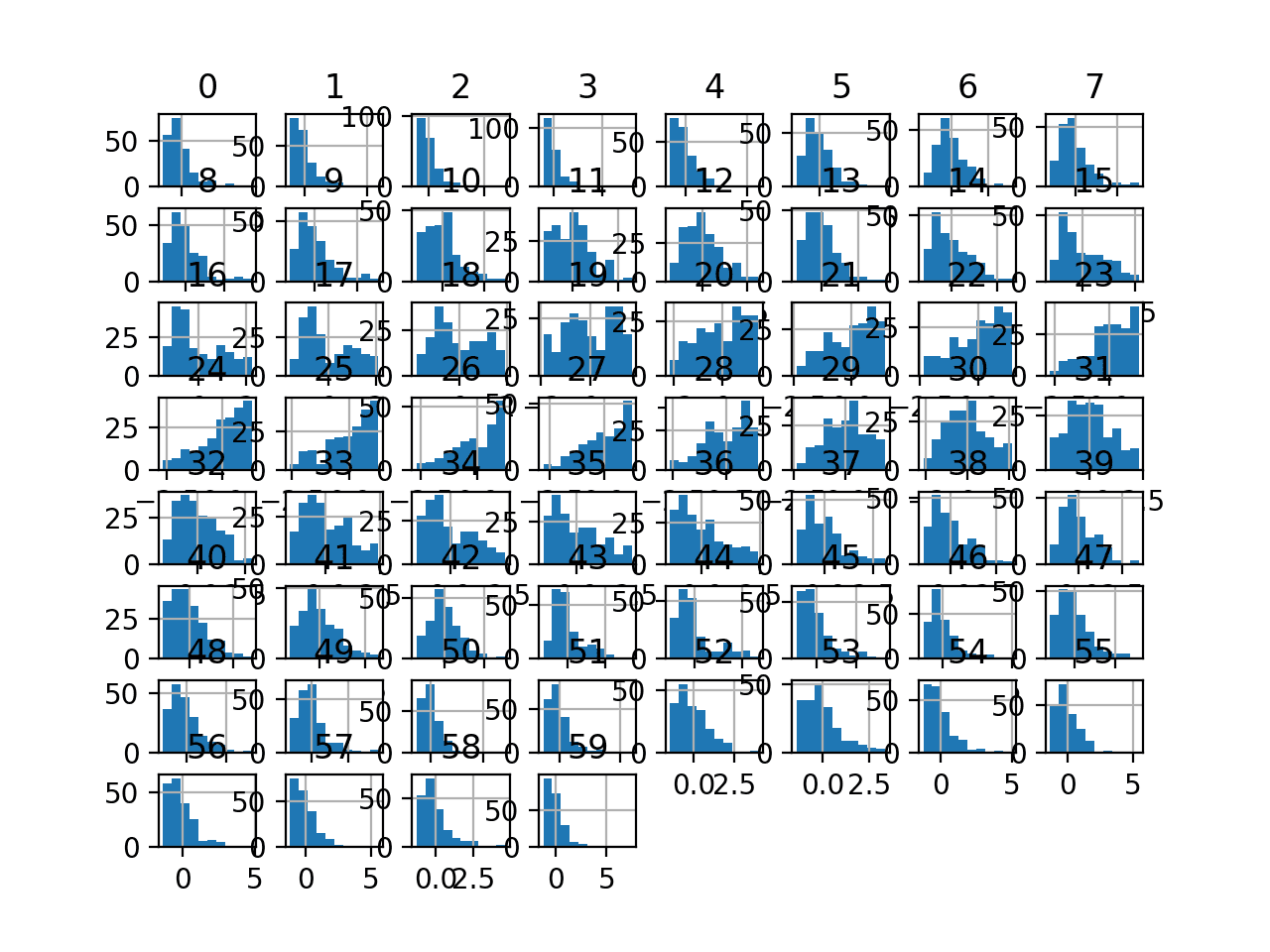
最后,为每个输入变量创建了一个直方图。
如果我们忽略图表的杂乱,只关注直方图本身,我们可以看到许多变量具有偏斜分布。
该数据集非常适合使用幂变换使变量更接近高斯分布。
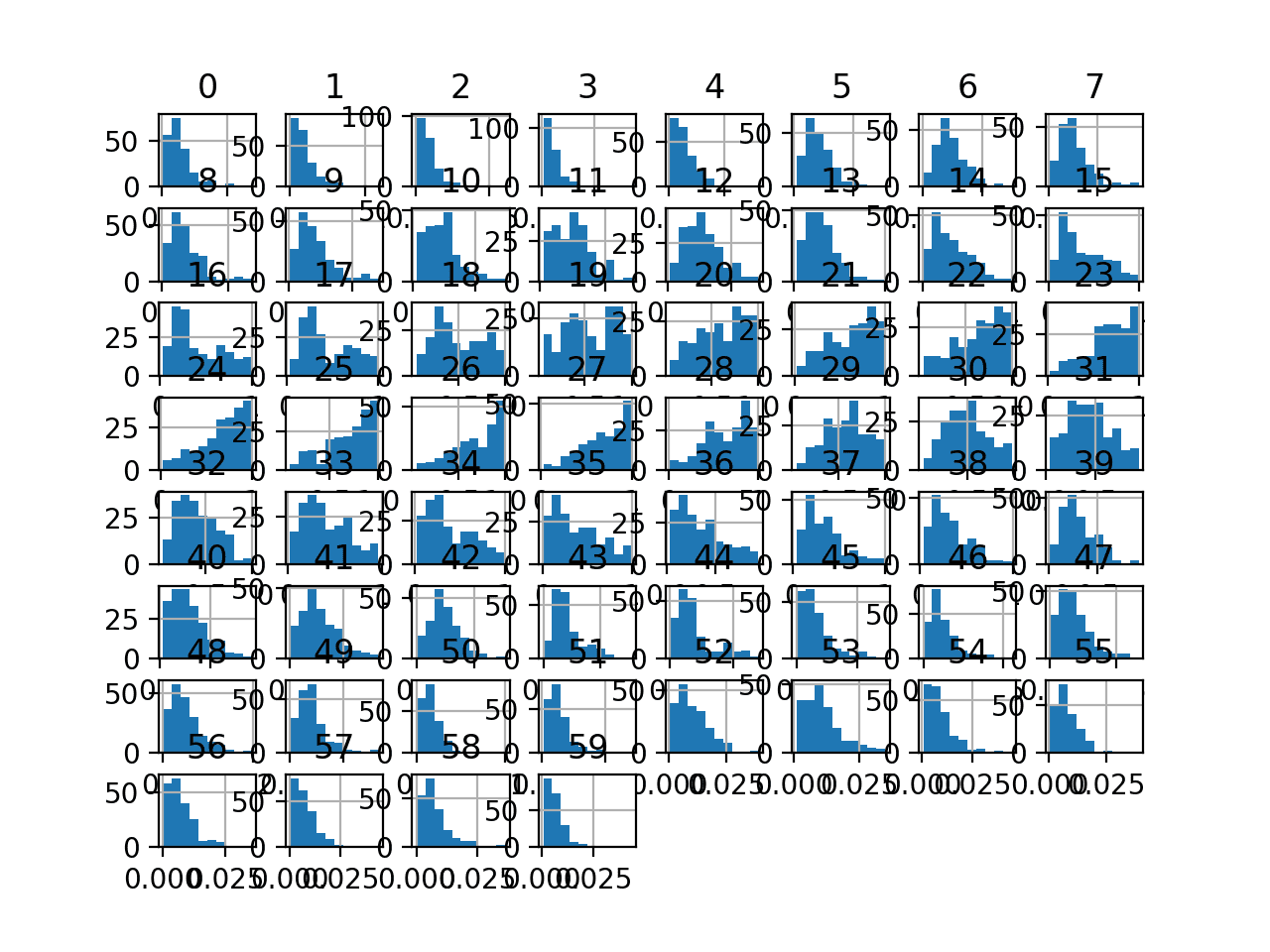
声纳二元分类数据集输入变量的直方图图
接下来,让我们在原始数据集上拟合和评估一个机器学习模型。
我们将使用默认超参数的 k-近邻算法,并使用重复分层 k 折交叉验证对其进行评估。完整的示例列在下面。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
# 在原始声纳数据集上评估 knn from numpy import mean from numpy import std from pandas import read_csv from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.neighbors import KNeighborsClassifier from sklearn.preprocessing import LabelEncoder from matplotlib import pyplot # 加载数据集 url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/sonar.csv" dataset = read_csv(url, header=None) data = dataset.values # 分割为输入和输出列 X, y = data[:, :-1], data[:, -1] # 确保输入是浮点数,输出是整数标签 X = X.astype('float32') y = LabelEncoder().fit_transform(y.astype('str')) # 定义和配置模型 model = KNeighborsClassifier() # 评估模型 cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) n_scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1, error_score='raise') # 报告模型性能 print('Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores))) |
运行示例评估 KNN 模型在原始声纳数据集上的性能。
注意:考虑到算法或评估过程的随机性,或数值精度的差异,您的结果可能会有所不同。请考虑多次运行示例并比较平均结果。
我们可以看到,该模型实现了大约 79.7% 的平均分类准确率,这表明它具有技能(优于 53.4%),并且接近良好性能(88%)。
|
1 |
准确率:0.797 (0.073) |
接下来,我们探讨数据集的 Box-Cox 幂变换。
Box-Cox 变换
Box-Cox 变换以该方法的两位作者命名。
它是一种幂变换,假设应用它的输入变量的值是严格正的。这意味着不支持 0 和负值。
需要注意的是,Box-Cox 过程只能应用于严格正的数据。
— 第 123 页,《特征工程与选择》,2019 年。
我们可以使用 PowerTransformer 类并设置“method”参数为“box-cox”来应用 Box-Cox 变换。定义后,我们可以调用 fit_transform() 函数并将其传递给我们的数据集,以创建我们数据集的 Box-Cox 变换版本。
|
1 2 3 |
... pt = PowerTransformer(method='box-cox') data = pt.fit_transform(data) |
我们的数据集没有负值,但可能有零值。这可能会导致问题。
我们还是试一下吧。
创建声纳数据集的 Box-Cox 变换并绘制结果直方图的完整示例列在下面。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# 可视化声纳数据集的 Box-Cox 变换 from pandas import read_csv from pandas import DataFrame from pandas.plotting import scatter_matrix from sklearn.preprocessing import PowerTransformer from matplotlib import pyplot # 加载数据集 url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/sonar.csv" dataset = read_csv(url, header=None) # 仅检索数字输入值 data = dataset.values[:, :-1] # 对数据集执行 Box-Cox 变换 pt = PowerTransformer(method='box-cox') data = pt.fit_transform(data) # 将数组转换回数据框 dataset = DataFrame(data) # 变量的直方图 dataset.hist() pyplot.show() |
运行该示例会导致以下错误
|
1 |
ValueError: Box-Cox 变换只能应用于严格正的数据 |
正如预期的那样,我们不能对原始数据使用变换,因为它不是严格正的。
解决此问题的一种方法是先使用 MixMaxScaler 变换将数据缩放到正值,然后应用变换。
我们可以使用 Pipeline 对象按顺序应用这两种变换;例如
|
1 2 3 4 5 6 |
... # 对数据集执行 Box-Cox 变换 scaler = MinMaxScaler(feature_range=(1, 2)) power = PowerTransformer(method='box-cox') pipeline = Pipeline(steps=[('s', scaler),('p', power)]) data = pipeline.fit_transform(data) |
将 Box-Cox 变换应用于缩放后的数据集的更新版本如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
# 可视化缩放后的声纳数据集的 Box-Cox 变换 from pandas import read_csv from pandas import DataFrame from pandas.plotting import scatter_matrix from sklearn.preprocessing import PowerTransformer 从 sklearn.预处理 导入 MinMaxScaler from sklearn.pipeline import Pipeline from matplotlib import pyplot # 加载数据集 url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/sonar.csv" dataset = read_csv(url, header=None) # 仅检索数字输入值 data = dataset.values[:, :-1] # 对数据集执行 Box-Cox 变换 scaler = MinMaxScaler(feature_range=(1, 2)) power = PowerTransformer(method='box-cox') pipeline = Pipeline(steps=[('s', scaler),('p', power)]) data = pipeline.fit_transform(data) # 将数组转换回数据框 dataset = DataFrame(data) # 变量的直方图 dataset.hist() pyplot.show() |
运行该示例会转换数据集并绘制每个输入变量的直方图。
我们可以看到,每个变量的直方图形状看起来比原始数据更接近高斯分布。

声纳数据集的 Box-Cox 变换输入变量的直方图
接下来,让我们评估与上一节相同的 KNN 模型,但这次是在 Box-Cox 变换的缩放数据集上。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
# 在 Box-Cox 声纳数据集上评估 knn from numpy import mean from numpy import std from pandas import read_csv from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.neighbors import KNeighborsClassifier from sklearn.preprocessing import LabelEncoder from sklearn.preprocessing import PowerTransformer 从 sklearn.预处理 导入 MinMaxScaler from sklearn.pipeline import Pipeline from matplotlib import pyplot # 加载数据集 url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/sonar.csv" dataset = read_csv(url, header=None) data = dataset.values # 分割为输入和输出列 X, y = data[:, :-1], data[:, -1] # 确保输入是浮点数,输出是整数标签 X = X.astype('float32') y = LabelEncoder().fit_transform(y.astype('str')) # 定义管道 scaler = MinMaxScaler(feature_range=(1, 2)) power = PowerTransformer(method='box-cox') model = KNeighborsClassifier() pipeline = Pipeline(steps=[('s', scaler),('p', power), ('m', model)]) # 评估管道 cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) n_scores = cross_val_score(pipeline, X, y, scoring='accuracy', cv=cv, n_jobs=-1, error_score='raise') # 报告管道性能 print('Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores))) |
注意:考虑到算法或评估过程的随机性,或数值精度的差异,您的结果可能会有所不同。请考虑多次运行示例并比较平均结果。
运行示例后,我们可以看到 Box-Cox 变换使性能从不进行变换的 79.7% 准确率提升到进行变换后的约 81.1%。
|
1 |
准确率:0.811 (0.085) |
接下来,让我们仔细看看 Yeo-Johnson 变换。
Yeo-Johnson 变换
Yeo-Johnson 变换也以作者的名字命名。
与 Box-Cox 变换不同,它不要求每个输入变量的值严格为正。它支持零值和负值。这意味着我们可以直接将其应用于我们的数据集,而无需先进行缩放。
我们可以通过定义一个 PowerTransform 对象并将“method”参数设置为“yeo-johnson”(默认值)来应用变换。
|
1 2 3 4 |
... # 对数据集执行 yeo-johnson 变换 pt = PowerTransformer(method='yeo-johnson') data = pt.fit_transform(data) |
下面的示例应用 Yeo-Johnson 变换并创建每个变换变量的直方图。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# 可视化声纳数据集的 Yeo-Johnson 变换 from pandas import read_csv from pandas import DataFrame from pandas.plotting import scatter_matrix from sklearn.preprocessing import PowerTransformer from matplotlib import pyplot # 加载数据集 url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/sonar.csv" dataset = read_csv(url, header=None) # 仅检索数字输入值 data = dataset.values[:, :-1] # 对数据集执行 yeo-johnson 变换 pt = PowerTransformer(method='yeo-johnson') data = pt.fit_transform(data) # 将数组转换回数据框 dataset = DataFrame(data) # 变量的直方图 dataset.hist() pyplot.show() |
运行该示例会转换数据集并绘制每个输入变量的直方图。
我们可以看到,每个变量的直方图形状看起来比原始数据更接近高斯分布,与 Box-Cox 变换非常相似。
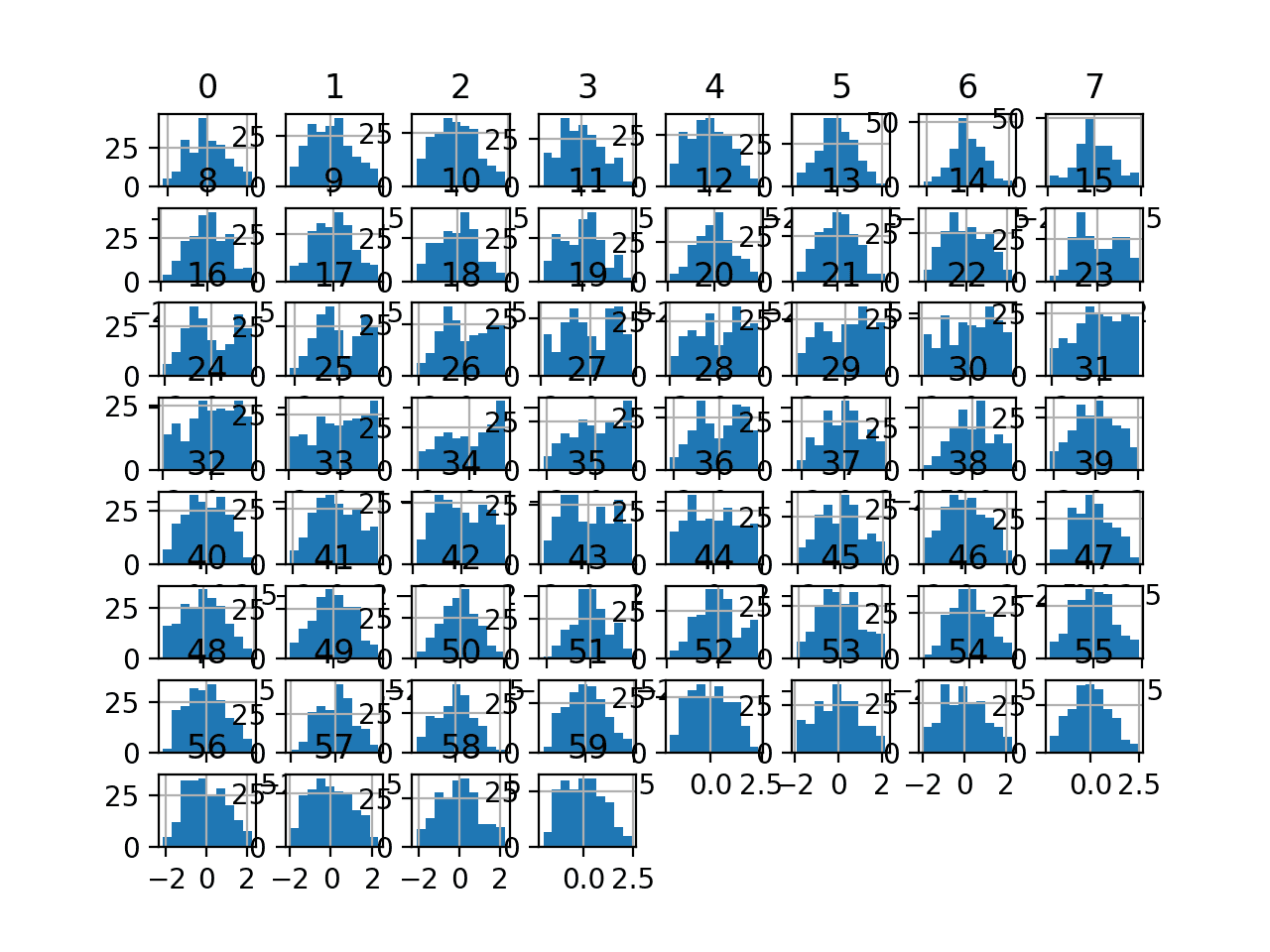
声纳数据集的 Yeo-Johnson 变换输入变量的直方图
接下来,我们将评估与上一节相同的 KNN 模型,但这次是在原始数据集的 Yeo-Johnson 变换上。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
# 在 Yeo-Johnson 声纳数据集上评估 knn from numpy import mean from numpy import std from pandas import read_csv from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.neighbors import KNeighborsClassifier from sklearn.preprocessing import LabelEncoder from sklearn.preprocessing import PowerTransformer 从 sklearn.预处理 导入 MinMaxScaler from sklearn.pipeline import Pipeline from matplotlib import pyplot # 加载数据集 url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/sonar.csv" dataset = read_csv(url, header=None) data = dataset.values # 分割为输入和输出列 X, y = data[:, :-1], data[:, -1] # 确保输入是浮点数,输出是整数标签 X = X.astype('float32') y = LabelEncoder().fit_transform(y.astype('str')) # 定义管道 power = PowerTransformer(method='yeo-johnson') model = KNeighborsClassifier() pipeline = Pipeline(steps=[('p', power), ('m', model)]) # 评估管道 cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) n_scores = cross_val_score(pipeline, X, y, scoring='accuracy', cv=cv, n_jobs=-1, error_score='raise') # 报告管道性能 print('Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores))) |
注意:考虑到算法或评估过程的随机性,或数值精度的差异,您的结果可能会有所不同。请考虑多次运行示例并比较平均结果。
运行示例后,我们可以看到 Yeo-Johnson 变换使性能从不进行变换的 79.7% 准确率提升到进行变换后的约 80.8%,低于 Box-Cox 变换实现的约 81.1%。
|
1 |
准确率:0.808 (0.082) |
有时,通过在执行 Yeo-Johnson 变换之前先标准化原始数据集,可以提高性能。
我们可以通过在管道中添加 StandardScaler 作为第一步来探索这一点。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
# 在 Yeo-Johnson 标准化的声纳数据集上评估 knn from numpy import mean from numpy import std from pandas import read_csv from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.neighbors import KNeighborsClassifier from sklearn.preprocessing import LabelEncoder from sklearn.preprocessing import PowerTransformer from sklearn.preprocessing import StandardScaler from sklearn.pipeline import Pipeline from matplotlib import pyplot # 加载数据集 url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/sonar.csv" dataset = read_csv(url, header=None) data = dataset.values # 分割为输入和输出列 X, y = data[:, :-1], data[:, -1] # 确保输入是浮点数,输出是整数标签 X = X.astype('float32') y = LabelEncoder().fit_transform(y.astype('str')) # 定义管道 scaler = StandardScaler() power = PowerTransformer(method='yeo-johnson') model = KNeighborsClassifier() pipeline = Pipeline(steps=[('s', scaler), ('p', power), ('m', model)]) # 评估管道 cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) n_scores = cross_val_score(pipeline, X, y, scoring='accuracy', cv=cv, n_jobs=-1, error_score='raise') # 报告管道性能 print('Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores))) |
注意:考虑到算法或评估过程的随机性,或数值精度的差异,您的结果可能会有所不同。请考虑多次运行示例并比较平均结果。
运行示例后,我们可以看到在 Yeo-Johnson 变换之前对数据进行标准化,使性能从大约 80.8% 提升到大约 81.6%,比 Box-Cox 变换的结果略有提升。
|
1 |
准确率:0.816 (0.077) |
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
教程
- 机器学习中的连续概率分布
- 如何在 Python 中使用幂变换进行时间序列预测数据
- 如何使用 Scikit-Learn 转换回归目标变量
- 如何转换数据以更好地适应正态分布
- 用于时间序列预测的 4 种常见机器学习数据转换
书籍
数据集 (Dataset)
API
文章
总结
在本教程中,您学习了如何在 scikit-learn 中使用幂变换,使变量更接近高斯分布以便进行建模。
具体来说,你学到了:
- 许多机器学习算法在数值变量服从高斯概率分布时表现更佳。
- 幂变换是一种将数值输入或输出变量转换为高斯分布或更接近高斯概率分布的技术。
- 如何在 scikit-learn 中使用 PowerTransform 来使用 Box-Cox 和 Yeo-Johnson 变换来为预测建模准备数据。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。



你好。我理解任何线性模型中都没有关于自变量分布的假设。你能澄清一下吗?
线性回归或逻辑回归等线性模型通常假设输入变量服从高斯分布。
嗨,Jason,
感谢这篇精彩的文章。
我的问题是,我看到你转换了整个数据集并在此基础上构建模型。
我非常困惑。这难道没有数据泄露吗?
请指教
在本教程中,我们只转换了整个数据以向您展示转换的效果。
教程中的建模示例使用 Pipeline 来避免数据泄露。如果这对您来说是个新概念,请参阅此
https://machinelearning.org.cn/data-preparation-without-data-leakage/
鉴于 MLE 正在估计 P(y | parameter, x) 的参数,您所说的“假设输入变量服从高斯分布”是指 P(x) ~ 高斯分布吗?
您好 oaixuroab…您是对的!感谢您的反馈!
亲爱的 Jason,
首先,感谢您触及这个话题,亲自动手解决这个话题非常有帮助。
我有两个在实践中探索数据转换过程时想到的问题。有没有关于如何首先做才能普遍拥有更健壮的过程的“黄金指南”?我的意思是,例如,您首先应用了缩放,然后进行了数据转换,但是首先进行数据转换然后进行缩放也可以找到类似的结果(我发现有时更好,有时更差的结果,这可能因不同的模型而异)。
此外,如果使用的数据包含负值甚至零值,Box-Cox 将返回“ValueError: The Box-Cox transformation can only be applied to strictly positive data”。
你知道在处理这类问题时仍然在管道中使用 Box-Cox 的方法吗?
非常感谢。
谢谢!
是的,先将数据缩放到正值,我发现范围 1 到 2 比 0e+5 到 1 更稳定。
你好,我将我的指数 1d 数组“Yeo-Johnson”应用于获得更多高斯数据,然后应用 Kde 并将我的 1d 数组分成 3 个簇。反正它效果更好,但我现在不知道如何取回我的原始数据值了?
太棒了!
你好 Jason,谢谢你,这很有帮助。
我有两个问题
我正在使用深度学习处理表格数据(回归)。
问题 1:我应该转换目标列吗?
问题 2:如果应该,那么当我部署模型进行新预测时,我会以转换后的方式获取目标,我该如何将其重新转换为原始数据值?
我去年黑色星期五购买了你所有的电子书 :) 我强烈推荐它们。
感谢你的出色工作。
试试看,看看是否能带来更好的性能。
是的!如果您使用管道,它会自动为您反转转换。
https://machinelearning.org.cn/how-to-transform-target-variables-for-regression-with-scikit-learn/
谢谢!
一如既往地精彩的课程。我非常喜欢阅读它,并且学到了很多。我还阅读了另外两篇关于分位数变换和离散化变换的相关文章。
我对代码的开头有一个愚蠢的问题,将 Panda 的数据框转换为 NumPy 数组(.values)是否必要?假设我们没有这样做,我们会得到相同的结果吗?或者它可能会导致转换器出现其他问题?
再次感谢您,请继续努力工作,
此致,
谢谢!
不,但我更喜欢直接使用 numpy 数组。
完美,感谢您的回复!
不客气。
标准化和幂变换之间的关键/独特区别是什么?
我理解(标准化是使它们处于相同的尺度),(幂变换是去除偏斜/稳定方差)。除此之外还有什么具体之处吗?提前感谢。
@Sam:值得一提的是,这两种变换都保持了变量内点的单调性。像随机森林这样的某些机器学习模型不受此类变换的影响,因此在那里测试/使用这些数据变换是不值得的。然而,在某些梯度提升树实现的情况下,我可以想象变量分箱方法可能依赖于幂变换的使用。
此致!
没关系,你说的很对。
亲爱的 Jason,一如既往,感谢这篇精彩的帖子!
我想知道关于“Box-Cox”方法,如果我只有零值(没有负值),我可以在转换之前将数据移动 0.001 或 1(或其他任何值)吗?
而不是使用 MixMaxScaler 变换?
我正在使用转换,然后应用迭代插补器(使用 BayesianRidge 估计器),所以我需要先转换我的数据。
谢谢!
伊迪特
是的,添加一个小数或缩放到新的正范围。
尝试几种方法,看看哪种效果好。
是的,我尝试了几种方法。有趣的是,无论我执行何种转换,迭代插补器在几次迭代后都会变得不稳定。似乎它陷入了一些超出范围值的糟糕反馈循环。然而,不执行任何转换到正态分布的替代选项会生成负的插补值,这是不合理的。
也许使用一些自定义代码来清理插补值或手动进行插补。
我会想办法的……非常感谢您的建议!
不客气。
如何将幂变换后的数据变回原始值尺度?例如,价格是目标变量,并被幂变换为正态分布。然后进行建模,预测的价格值需要使用底层变换函数转换回实际尺度。我该如何做?顺便说一下,这是一篇很棒的帖子!!谢谢!
如果您转换了目标,那么您可能需要反转模型所做预测的转换。
如果转换只应用于输入,则不需要反转转换。
嗨,Jason,
我有一个时间序列数据集(间隔=季度;多索引=(年份,季度),列=财务方面(例如应付账款))。
我没有提供 lambda 值,我让估计器估计 lambda 参数。
有些“X_columns”不适合 Yeo-Johnson 变换,而这些相同的列适合 BoxCox。
多次运行后,一致结果如下所示
Y-J 后 X_column 结果图:创建了一条水平线 (y=0.25),lambda = -3.99
B-C 后 X_column 结果图:预期结果,lambda = 0.00232
问题 1)您能提供这种结果差异的理论依据吗?
问题 2)B-C 和 Y-J 都“最大化对数似然函数”来估计 lambda,那么噪声从何而来?
你说的理论依据是什么意思?你可以手动进行计算,看看算法是如何得出结果的。
嗨,Jason,
是先缩放数据然后应用变换好,还是反之?
你在例子中就是这样做的
非常感谢
一如既往地非常有用! 🙂
我忘了再问一件事
一个包含 3 个任务的管道
A) Smote
B) PowerTransformer
C) MinMaxScaler
在管道中我应该以什么顺序执行这些步骤?
谢谢!
也许可以尝试一下,看看哪种顺序能为您的特定数据集和模型带来最佳性能。
我猜是 minmax,power,然后是 smote。
是的,我试过了,确实更好了。
谢谢 Jason,我真的很感激 🙂
干得好。
先缩放再转换。
感谢您发布这些内容,它完全有助于使事情更清晰
不客气!
你好 Jason。首先,感谢你出色的工作。我对本教程有一个疑问:当你将 PowerTransformer 引入 Pipeline 时,它也会转换目标数据吗?
我也强烈推荐购买您的课程,它们物有所值!
谢谢你
不客气。
不,管道只应用于输入。
谢谢!!!
你好,Jason!
这是一篇非常有趣的文章!!
幂变换对深度学习也有用吗?
谢谢
谢谢。
是的!
“有些算法,如线性回归和逻辑回归,明确假设实值变量服从高斯分布。”
不!逻辑回归并不与线性回归做出相同的假设。预测变量不需要正态分布。
好的,谢谢。
先生,我需要一个帮助。我已经对我的高斯过程回归的特征和目标参数都应用了分位数变换。但最终,我想在性能计算期间将点转换回。我该怎么做?有没有可用于此的库?
您可以在对象上调用 inverse_transform() 并传入数据。
嗨,Jason,
您能否解释一下将数据转换为类高斯分布在多大程度上会损害数据的有效性?
谢谢,
Keyvan
不完全是,这可能取决于数据和领域的具体情况。
您能否详细解释一下哪些数据规格和领域可能在机器学习应用中进行转换后破坏数据的有效性?
任何相关的参考文献也将不胜感激。
谢谢,
我推荐查阅“进一步阅读”部分列出的参考文献。
您能否提及非线性变换的缺点吗?无论是幂变换还是分位数变换?
您好 Esmat…以下资源可能有助于理解如何以及何时使用幂变换。
https://www.yourdatateacher.com/2021/04/21/when-and-how-to-use-power-transform-in-machine-learning/
非常感谢信息
不客气,Reyhan!
如果将 Yeo-Johnson 或 Box-Cox 应用于整个数据集,是否存在数据泄露的风险?
嗨 Ben……以下内容可能会让您感兴趣
https://machinelearning.org.cn/data-leakage-machine-learning/
亲爱的 Jason,
感谢您提供的真正有帮助且鼓舞人心的博客/网站——内容太棒了。
关于这篇文章和 Box-Cox 幂变换,我有一个问题:
是否可以只对我的数据集中选定的特征进行 Box-Cox 变换?现在我收到一个 ValueError(“Data must not be constant”),原因是我数据集中包含几个 0/1 特征。这主要是由于管道开头的独热编码变换造成的……如果可以只对选定的特征进行 Box-Cox 幂变换,我就能有一个“干净”的管道。还是我漏掉了什么简单的东西?
提前感谢!
诚挚的问候,
马兹。
嗨,Mads……以下讨论可能对您有所帮助
https://stackoverflow.com/questions/62116192/valueerror-data-must-not-be-constant