如何识别生成对抗网络训练过程中的不稳定模型。
GAN 很难训练。
它们之所以难以训练,是因为生成器模型和判别器模型在一个零和博弈中同时进行训练。这意味着一个模型的改进是以牺牲另一个模型为代价的。
训练两个模型的目标是找到两个相互竞争的顾虑点之间的平衡点。
这也意味着,每次更新其中一个模型的参数时,所解决的优化问题的性质都会发生变化。这就产生了动态系统的效果。从神经网络的角度来看,同时训练两个竞争性神经网络的技术挑战在于它们可能无法收敛。
重要的是要对GAN模型的正常收敛和GAN模型的异常收敛(有时称为故障模式)产生直觉。
在本教程中,我们将首先为简单的图像生成任务开发一个稳定的GAN模型,以确定正常收敛是什么样的,以及通常会遇到什么。
然后,我们将以不同的方式损害GAN模型,并探索在训练GAN模型时可能会遇到的一系列故障模式。这些场景将帮助您培养对GAN模型未能训练时需要查找或预期什么的直觉,以及如何处理它们的想法。
完成本教程后,您将了解:
- 如何通过查看生成器和判别器随时间的损失来识别稳定的GAN训练过程。
- 如何通过查看学习曲线和生成的图像来识别模式崩溃。
- 如何通过查看生成器和判别器随时间的损失的学习曲线来识别收敛失败。
通过我的新书《Python生成对抗网络》启动您的项目,其中包括分步教程和所有示例的Python源代码文件。
让我们开始吧。
- 更新于2020年8月:纠正了折线图上的标签。
- 2021 年 1 月更新:已更新,以便层冻结与批处理归一化一起使用。
- 更新于2021年1月:简化了模型架构,以确保我们能看到故障。

生成对抗网络故障模式的实用指南
照片来自 Jason Heavner,部分权利保留。
教程概述
本教程分为三个部分;它们是:
- 如何识别稳定的生成对抗网络
- 如何在生成对抗网络中识别模式崩溃
- 如何识别生成对抗网络中的收敛失败
如何训练稳定的生成对抗网络
在本节中,我们将训练一个稳定的GAN来生成手写数字的图像。
具体来说,我们将使用MNIST手写数字数据集中的数字“8”。
该模型的运行结果将建立一个稳定的GAN,用于后续实验,并为稳定的GAN训练过程的生成图像和学习曲线提供一个配置。
第一步是定义模型。
判别器模型接收一个28×28的灰度图像作为输入,并输出一个二元预测,判断图像是真实的(类别=1)还是伪造的(类别=0)。它被实现为一个适度的卷积神经网络,采用了GAN设计的最佳实践,例如使用斜率为0.2的LeakyReLU激活函数、2×2步幅进行下采样,以及Adam优化器(一种随机梯度下降变体),学习率为0.0002,动量为0.5。
下面的define_discriminator()函数实现了这一点,定义并编译了判别器模型并返回它。图像的输入形状被参数化为一个默认的函数参数,以使其清晰。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# 定义独立的判别器模型 def define_discriminator(in_shape=(28,28,1)): # 权重初始化 init = RandomNormal(stddev=0.02) # 定义模型 model = Sequential() # 下采样到 14x14 model.add(Conv2D(64, (4,4), strides=(2,2), padding='same', kernel_initializer=init, input_shape=in_shape)) model.add(LeakyReLU(alpha=0.2)) # 下采样到 7x7 model.add(Conv2D(64, (4,4), strides=(2,2), padding='same', kernel_initializer=init)) model.add(LeakyReLU(alpha=0.2)) # 分类器 model.add(Flatten()) model.add(Dense(1, activation='sigmoid')) # 编译模型 opt = Adam(lr=0.0002, beta_1=0.5) model.compile(loss='binary_crossentropy', optimizer=opt, metrics=['accuracy']) return model |
生成器模型接收潜在空间中的一个点作为输入,并输出一个28×28的灰度图像。这是通过使用一个全连接层来解释潜在空间中的点,并提供足够的激活来将其重塑为输出图像的低分辨率版本(例如7×7)的许多副本(在本例中为128个)来实现的。然后,它通过转置卷积层对输出图像进行两次上采样,每次都使激活的大小加倍,面积增加四倍。该模型使用了最佳实践,例如LeakyReLU激活、核大小是步幅大小的因子,以及输出层中的双曲正切(tanh)激活函数。
想从零开始开发GAN吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
下面的define_generator()函数定义了生成器模型,但有意不编译它,因为它不直接训练,然后返回模型。潜在空间的大小被参数化为一个函数参数。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
# 定义独立的生成器模型 def define_generator(latent_dim): # 权重初始化 init = RandomNormal(stddev=0.02) # 定义模型 model = Sequential() # 7x7 图像的基础 n_nodes = 128 * 7 * 7 model.add(Dense(n_nodes, kernel_initializer=init, input_dim=latent_dim)) model.add(LeakyReLU(alpha=0.2)) model.add(Reshape((7, 7, 128))) # 上采样到 14x14 model.add(Conv2DTranspose(128, (4,4), strides=(2,2), padding='same', kernel_initializer=init)) model.add(LeakyReLU(alpha=0.2)) # 上采样到 28x28 model.add(Conv2DTranspose(128, (4,4), strides=(2,2), padding='same', kernel_initializer=init)) model.add(LeakyReLU(alpha=0.2)) # 输出 28x28x1 model.add(Conv2D(1, (7,7), activation='tanh', padding='same', kernel_initializer=init)) return model |
接下来,可以定义一个GAN模型,将生成器模型和判别器模型组合成一个更大的模型。这个更大的模型将用于通过判别器模型的输出和计算出的误差来训练生成器中的模型权重。判别器模型是单独训练的,因此,在这个组合的GAN模型中,判别器模型的权重被标记为不可训练,以确保只有生成器模型的权重被更新。判别器权重的可训练性变化只在训练组合GAN模型时生效,在单独训练判别器时则不会。
这个更大的GAN模型以潜在空间中的一个点作为输入,使用生成器模型生成图像,然后将该图像作为输入馈送给判别器模型,然后输出或分类为真或假。
下面的define_gan()函数实现了这一点,它以已定义的生成器和判别器模型作为输入。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# 定义组合的生成器和判别器模型,用于更新生成器 def define_gan(generator, discriminator): # 使判别器中的权重不可训练 discriminator.trainable = False # 连接它们 model = Sequential() # 添加生成器 model.add(generator) # 添加判别器 model.add(discriminator) # 编译模型 opt = Adam(lr=0.0002, beta_1=0.5) model.compile(loss='binary_crossentropy', optimizer=opt) return model |
现在我们已经定义了GAN模型,我们需要训练它。但是,在训练模型之前,我们需要输入数据。
第一步是加载和缩放MNIST数据集。通过调用Keras的load_data()函数加载整个数据集,然后选择属于类别8(例如,手写数字8)的图像子集(约5000张)。然后必须将像素值缩放到[-1,1]的范围,以匹配生成器模型的输出。
下面的load_real_samples()函数实现了这一点,它返回已加载和缩放的MNIST训练数据集的子集,为建模做好准备。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# 加载mnist图像 def load_real_samples(): # 加载数据集 (trainX, trainy), (_, _) = load_data() # 扩展到3D,例如添加通道 X = expand_dims(trainX, axis=-1) # 选择给定类别的所有样本 selected_ix = trainy == 8 X = X[selected_ix] # 从整数转换为浮点数 X = X.astype('float32') # 从 [0,255] 缩放到 [-1,1] X = (X - 127.5) / 127.5 return X |
我们需要在每次更新GAN模型时,从数据集中获取一个(或半个)批次的真实图像。一个简单的方法是每次都从数据集中选择一个随机样本。
下面的generate_real_samples()函数实现了这一点,它接收准备好的数据集作为参数,选择并返回一个随机的脸部图像样本及其对应的类别标签,供判别器使用,具体来说是类别=1,表示它们是真实的图像。
|
1 2 3 4 5 6 7 8 9 |
# 选择真实样本 def generate_real_samples(dataset, n_samples): # 选择随机实例 ix = randint(0, dataset.shape[0], n_samples) # 选择图像 X = dataset[ix] # 生成类别标签 y = ones((n_samples, 1)) return X, y |
接下来,我们需要为生成器模型提供输入。这些是来自潜在空间的随机点,具体来说是高斯分布的随机变量。
下面的generate_latent_points()函数实现了这一点,它接收潜在空间的尺寸作为参数以及所需的点数,并将它们作为一个批次的输入样本返回给生成器模型。
|
1 2 3 4 5 6 7 |
# 在潜在空间中生成点作为生成器的输入 def generate_latent_points(latent_dim, n_samples): # 在潜在空间中生成点 x_input = randn(latent_dim * n_samples) # 重塑为网络的输入批次 x_input = x_input.reshape(n_samples, latent_dim) return x_input |
接下来,我们需要使用潜在空间中的点作为生成器的输入,以生成新的图像。
下面的generate_fake_samples()函数实现了这一点,它接收生成器模型和潜在空间的大小作为参数,然后生成潜在空间中的点并使用它们作为生成器模型的输入。该函数返回生成的图像及其对应的类别标签,供判别器模型使用,具体来说是类别=0,表示它们是伪造的或生成的。
|
1 2 3 4 5 6 7 8 9 |
# 使用生成器生成 n 个假示例,并带有类别标签 def generate_fake_samples(generator, latent_dim, n_samples): # 在潜在空间中生成点 x_input = generate_latent_points(latent_dim, n_samples) # 预测输出 X = generator.predict(x_input) # 创建类别标签 y = zeros((n_samples, 1)) return X, y |
我们需要记录模型的性能。也许评估GAN性能最可靠的方法是使用生成器生成图像,然后进行审查和主观评估。
下面的summarize_performance()函数在训练过程中的特定时间点接收生成器模型,并使用它生成100张图像,将它们排列成10×10的网格,然后进行绘制并保存到文件。此时模型也会被保存到文件,以防我们想稍后使用它来生成更多图像。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# 生成样本并保存为图,并保存模型 def summarize_performance(step, g_model, latent_dim, n_samples=100): # 准备伪示例 X, _ = generate_fake_samples(g_model, latent_dim, n_samples) # 将范围从[-1,1]缩放到[0,1] X = (X + 1) / 2.0 # 绘制图像 for i in range(10 * 10): # 定义子图 pyplot.subplot(10, 10, 1 + i) # 关闭轴线 pyplot.axis('off') # 绘制原始像素数据 pyplot.imshow(X[i, :, :, 0], cmap='gray_r') # 保存图到文件 pyplot.savefig('results_baseline/generated_plot_%03d.png' % (step+1)) pyplot.close() # 保存生成器模型 g_model.save('results_baseline/model_%03d.h5' % (step+1)) |
除了图像质量之外,跟踪模型随时间的损失和准确率也是一个好主意。
可以跟踪判别器对真实样本和伪造样本的损失和分类准确率,以及生成器在每次更新时的损失。然后,可以在训练结束时使用这些信息来创建损失和准确率的折线图。
下面的plot_history()函数实现了这一点,并将结果保存到文件。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
# 创建GAN损失的折线图并保存到文件 def plot_history(d1_hist, d2_hist, g_hist, a1_hist, a2_hist): # 绘制损失 pyplot.subplot(2, 1, 1) pyplot.plot(d1_hist, label='d-real') pyplot.plot(d2_hist, label='d-fake') pyplot.plot(g_hist, label='gen') pyplot.legend() # 绘制判别器准确率 pyplot.subplot(2, 1, 2) pyplot.plot(a1_hist, label='acc-real') pyplot.plot(a2_hist, label='acc-fake') pyplot.legend() # 保存图到文件 pyplot.savefig('results_baseline/plot_line_plot_loss.png') pyplot.close() |
我们现在准备好拟合GAN模型了。
该模型训练10个训练周期,这只是一个任意值,因为模型可能在最初几个周期后就开始生成类似数字8的数字。使用了128个样本的批次大小,每个训练周期包含5851/128,即大约45个批次的真实和伪造样本以及模型更新。因此,模型被训练了10个周期,每个周期45个批次,共计450次迭代。
首先,判别器模型用一个半批次的真实样本进行更新,然后用一个半批次的伪造样本进行更新,两者共同构成一个批次的权重更新。然后通过复合GAN模型更新生成器。重要的是,伪造样本的类别标签被设置为1,即真实。这会有效地更新生成器,使其在下一个批次中更擅长生成真实样本。
下面的train()函数实现了这一点,它接收定义的模型、数据集和潜在维度大小作为参数,并使用默认参数来设置周期数和批次大小。生成器模型在训练结束时被保存。
判别器和生成器模型的性能在每个迭代中都会被报告。样本图像每周期生成并保存,模型性能的折线图在运行结束时创建并保存。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
# 训练生成器和判别器 def train(g_model, d_model, gan_model, dataset, latent_dim, n_epochs=10, n_batch=128): # 计算每个周期的批次数 bat_per_epo = int(dataset.shape[0] / n_batch) # 根据批次和周期计算总迭代次数 n_steps = bat_per_epo * n_epochs # 计算半个批次中的样本数 half_batch = int(n_batch / 2) # 准备用于存储每次迭代统计信息的列表 d1_hist, d2_hist, g_hist, a1_hist, a2_hist = list(), list(), list(), list(), list() # 手动枚举 epoch for i in range(n_steps): # 获取随机选择的“真实”样本 X_real, y_real = generate_real_samples(dataset, half_batch) # 更新判别器模型权重 d_loss1, d_acc1 = d_model.train_on_batch(X_real, y_real) # 生成“假”示例 X_fake, y_fake = generate_fake_samples(g_model, latent_dim, half_batch) # 更新判别器模型权重 d_loss2, d_acc2 = d_model.train_on_batch(X_fake, y_fake) # 准备潜在空间中的点作为生成器的输入 X_gan = generate_latent_points(latent_dim, n_batch) # 为伪样本创建反转标签 y_gan = ones((n_batch, 1)) # 通过判别器的误差更新生成器 g_loss = gan_model.train_on_batch(X_gan, y_gan) # 总结此批次的损失 print('>%d, d1=%.3f, d2=%.3f g=%.3f, a1=%d, a2=%d' % (i+1, d_loss1, d_loss2, g_loss, int(100*d_acc1), int(100*d_acc2))) # 记录历史 d1_hist.append(d_loss1) d2_hist.append(d_loss2) g_hist.append(g_loss) a1_hist.append(d_acc1) a2_hist.append(d_acc2) # 每“个周期”评估模型性能 if (i+1) % bat_per_epo == 0: summarize_performance(i, g_model, latent_dim) plot_history(d1_hist, d2_hist, g_hist, a1_hist, a2_hist) |
现在所有函数都已定义,我们可以创建用于存储图像和模型的目录(在此例中为“*results_baseline*”),创建模型,加载数据集,并开始训练过程。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
# 为结果创建文件夹 makedirs('results_baseline', exist_ok=True) # 潜在空间的大小 latent_dim = 50 # 创建判别器 discriminator = define_discriminator() # 创建生成器 generator = define_generator(latent_dim) # 创建GAN gan_model = define_gan(generator, discriminator) # 加载图像数据 dataset = load_real_samples() print(dataset.shape) # 训练模型 train(generator, discriminator, gan_model, dataset, latent_dim) |
将所有这些联系在一起,完整的示例如下。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 |
# 训练一个用于生成手写数字的稳定 GAN 的示例 from os import makedirs from numpy import expand_dims from numpy import zeros from numpy import ones from numpy.random import randn from numpy.random import randint from keras.datasets.mnist import load_data from keras.optimizers import Adam from keras.models import Sequential from keras.layers import Dense from keras.layers import Reshape from keras.layers import Flatten 从 keras.layers 导入 Conv2D from keras.layers import Conv2DTranspose from keras.layers import LeakyReLU from keras.initializers import RandomNormal from matplotlib import pyplot # 定义独立的判别器模型 def define_discriminator(in_shape=(28,28,1)): # 权重初始化 init = RandomNormal(stddev=0.02) # 定义模型 model = Sequential() # 下采样到 14x14 model.add(Conv2D(64, (4,4), strides=(2,2), padding='same', kernel_initializer=init, input_shape=in_shape)) model.add(LeakyReLU(alpha=0.2)) # 下采样到 7x7 model.add(Conv2D(64, (4,4), strides=(2,2), padding='same', kernel_initializer=init)) model.add(LeakyReLU(alpha=0.2)) # 分类器 model.add(Flatten()) model.add(Dense(1, activation='sigmoid')) # 编译模型 opt = Adam(lr=0.0002, beta_1=0.5) model.compile(loss='binary_crossentropy', optimizer=opt, metrics=['accuracy']) return model # 定义独立的生成器模型 def define_generator(latent_dim): # 权重初始化 init = RandomNormal(stddev=0.02) # 定义模型 model = Sequential() # 7x7 图像的基础 n_nodes = 128 * 7 * 7 model.add(Dense(n_nodes, kernel_initializer=init, input_dim=latent_dim)) model.add(LeakyReLU(alpha=0.2)) model.add(Reshape((7, 7, 128))) # 上采样到 14x14 model.add(Conv2DTranspose(128, (4,4), strides=(2,2), padding='same', kernel_initializer=init)) model.add(LeakyReLU(alpha=0.2)) # 上采样到 28x28 model.add(Conv2DTranspose(128, (4,4), strides=(2,2), padding='same', kernel_initializer=init)) model.add(LeakyReLU(alpha=0.2)) # 输出 28x28x1 model.add(Conv2D(1, (7,7), activation='tanh', padding='same', kernel_initializer=init)) return model # 定义组合的生成器和判别器模型,用于更新生成器 def define_gan(generator, discriminator): # 使判别器中的权重不可训练 discriminator.trainable = False # 连接它们 model = Sequential() # 添加生成器 model.add(generator) # 添加判别器 model.add(discriminator) # 编译模型 opt = Adam(lr=0.0002, beta_1=0.5) model.compile(loss='binary_crossentropy', optimizer=opt) return model # 加载mnist图像 def load_real_samples(): # 加载数据集 (trainX, trainy), (_, _) = load_data() # 扩展到3D,例如添加通道 X = expand_dims(trainX, axis=-1) # 选择给定类别的所有样本 selected_ix = trainy == 8 X = X[selected_ix] # 从整数转换为浮点数 X = X.astype('float32') # 从 [0,255] 缩放到 [-1,1] X = (X - 127.5) / 127.5 return X # 选择真实样本 def generate_real_samples(dataset, n_samples): # 选择随机实例 ix = randint(0, dataset.shape[0], n_samples) # 选择图像 X = dataset[ix] # 生成类别标签 y = ones((n_samples, 1)) 返回 X, y # 在潜在空间中生成点作为生成器的输入 def generate_latent_points(latent_dim, n_samples): # 在潜在空间中生成点 x_input = randn(latent_dim * n_samples) # 重塑为网络的输入批次 x_input = x_input.reshape(n_samples, latent_dim) return x_input # 使用生成器生成 n 个假示例,并带有类别标签 def generate_fake_samples(generator, latent_dim, n_samples): # 在潜在空间中生成点 x_input = generate_latent_points(latent_dim, n_samples) # 预测输出 X = generator.predict(x_input) # 创建类别标签 y = zeros((n_samples, 1)) 返回 X, y # 生成样本并保存为图,并保存模型 def summarize_performance(step, g_model, latent_dim, n_samples=100): # 准备伪示例 X, _ = generate_fake_samples(g_model, latent_dim, n_samples) # 将范围从[-1,1]缩放到[0,1] X = (X + 1) / 2.0 # 绘制图像 for i in range(10 * 10): # 定义子图 pyplot.subplot(10, 10, 1 + i) # 关闭轴线 pyplot.axis('off') # 绘制原始像素数据 pyplot.imshow(X[i, :, :, 0], cmap='gray_r') # 保存图到文件 pyplot.savefig('results_baseline/generated_plot_%03d.png' % (step+1)) pyplot.close() # 保存生成器模型 g_model.save('results_baseline/model_%03d.h5' % (step+1)) # 创建GAN损失的折线图并保存到文件 def plot_history(d1_hist, d2_hist, g_hist, a1_hist, a2_hist): # 绘制损失 pyplot.subplot(2, 1, 1) pyplot.plot(d1_hist, label='d-real') pyplot.plot(d2_hist, label='d-fake') pyplot.plot(g_hist, label='gen') pyplot.legend() # 绘制判别器准确率 pyplot.subplot(2, 1, 2) pyplot.plot(a1_hist, label='acc-real') pyplot.plot(a2_hist, label='acc-fake') pyplot.legend() # 保存图到文件 pyplot.savefig('results_baseline/plot_line_plot_loss.png') pyplot.close() # 训练生成器和判别器 def train(g_model, d_model, gan_model, dataset, latent_dim, n_epochs=10, n_batch=128): # 计算每个周期的批次数 bat_per_epo = int(dataset.shape[0] / n_batch) # 根据批次和周期计算总迭代次数 n_steps = bat_per_epo * n_epochs # 计算半个批次中的样本数 half_batch = int(n_batch / 2) # 准备用于存储每次迭代统计信息的列表 d1_hist, d2_hist, g_hist, a1_hist, a2_hist = list(), list(), list(), list(), list() # 手动枚举 epoch for i in range(n_steps): # 获取随机选择的“真实”样本 X_real, y_real = generate_real_samples(dataset, half_batch) # 更新判别器模型权重 d_loss1, d_acc1 = d_model.train_on_batch(X_real, y_real) # 生成“假”示例 X_fake, y_fake = generate_fake_samples(g_model, latent_dim, half_batch) # 更新判别器模型权重 d_loss2, d_acc2 = d_model.train_on_batch(X_fake, y_fake) # 准备潜在空间中的点作为生成器的输入 X_gan = generate_latent_points(latent_dim, n_batch) # 为伪样本创建反转标签 y_gan = ones((n_batch, 1)) # 通过判别器的误差更新生成器 g_loss = gan_model.train_on_batch(X_gan, y_gan) # 总结此批次的损失 print('>%d, d1=%.3f, d2=%.3f g=%.3f, a1=%d, a2=%d' % (i+1, d_loss1, d_loss2, g_loss, int(100*d_acc1), int(100*d_acc2))) # 记录历史 d1_hist.append(d_loss1) d2_hist.append(d_loss2) g_hist.append(g_loss) a1_hist.append(d_acc1) a2_hist.append(d_acc2) # 每“个周期”评估模型性能 if (i+1) % bat_per_epo == 0: summarize_performance(i, g_model, latent_dim) plot_history(d1_hist, d2_hist, g_hist, a1_hist, a2_hist) # 为结果创建文件夹 makedirs('results_baseline', exist_ok=True) # 潜在空间的大小 latent_dim = 50 # 创建判别器 discriminator = define_discriminator() # 创建生成器 generator = define_generator(latent_dim) # 创建GAN gan_model = define_gan(generator, discriminator) # 加载图像数据 dataset = load_real_samples() print(dataset.shape) # 训练模型 train(generator, discriminator, gan_model, dataset, latent_dim) |
运行示例很快,在没有 GPU 的现代硬件上大约需要 10 分钟。
您的具体结果将因学习算法的随机性而异。尽管如此,训练的总体结构应该非常相似。
首先,鉴别器损失和准确性以及生成器模型的损失会报告给控制台,每个训练循环迭代一次。
这很重要。稳定的 GAN 将具有大约 0.5 的鉴别器损失,通常在 0.5 到可能高达 0.7 或 0.8 之间。生成器损失通常更高,可能在 1.0、1.5、2.0 甚至更高附近徘徊。
鉴别器在真实图像和生成(假)图像上的准确性不会是 50%,但通常应该在 70% 到 80% 左右徘徊。
对于鉴别器和生成器,行为很可能一开始是不稳定的,并且在模型收敛到稳定平衡之前会发生很多变化。
|
1 2 3 4 5 6 7 8 9 10 11 |
>1, d1=0.859, d2=0.664 g=0.872, a1=37, a2=59 >2, d1=0.190, d2=1.429 g=0.555, a1=100, a2=10 >3, d1=0.094, d2=1.467 g=0.597, a1=100, a2=4 >4, d1=0.097, d2=1.315 g=0.686, a1=100, a2=9 >5, d1=0.100, d2=1.241 g=0.714, a1=100, a2=9 ... >446, d1=0.593, d2=0.546 g=1.330, a1=76, a2=82 >447, d1=0.551, d2=0.739 g=0.981, a1=82, a2=39 >448, d1=0.628, d2=0.505 g=1.420, a1=79, a2=89 >449, d1=0.641, d2=0.533 g=1.381, a1=60, a2=85 >450, d1=0.550, d2=0.731 g=1.100, a1=76, a2=42 |
在运行结束时创建并保存损失和准确性的折线图。
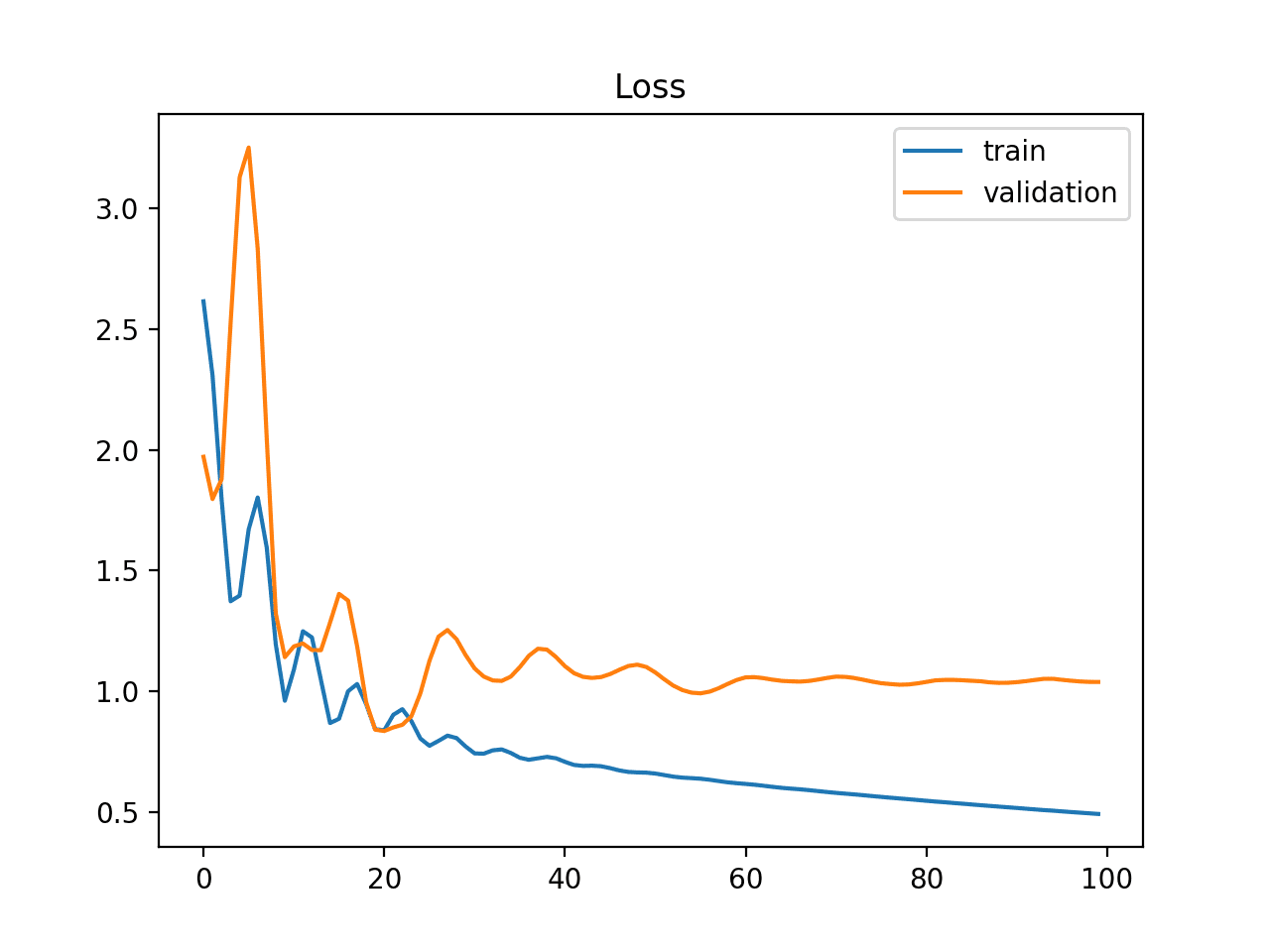
该图包含两个子图。顶部子图显示真实图像的鉴别器损失(蓝色)、生成假图像的鉴别器损失(橙色)和生成假图像的生成器损失(绿色)的折线图。
我们可以看到,所有三项损失在运行早期都有点不稳定,然后在第 100 到 300 个周期稳定下来。之后,损失保持稳定,尽管方差有所增加。
这是训练期间正常或预期损失的示例。也就是说,真实和假样本的鉴别器损失在大约 0.5 处大致相同,而生成器的损失略高,在 0.5 到 2.0 之间。如果生成器模型能够生成合理的图像,那么期望这些图像会在第 100 到 300 个周期之间生成,并且很可能也会在第 300 到 450 个周期之间生成。
底部子图显示了训练期间鉴别器在真实(蓝色)和假(橙色)图像上的准确性折线图。我们看到与损失子图类似的结构,即准确性在两种图像类型之间一开始差异很大,然后在第 100 到 300 个周期稳定在 70% 到 80% 左右,并在此之后保持稳定,尽管方差有所增加。
这些模式的时间尺度(例如,迭代次数或训练周期)和绝对值将因问题和 GAN 模型类型而异,尽管该图为稳定 GAN 模型训练时的预期提供了良好的基准。
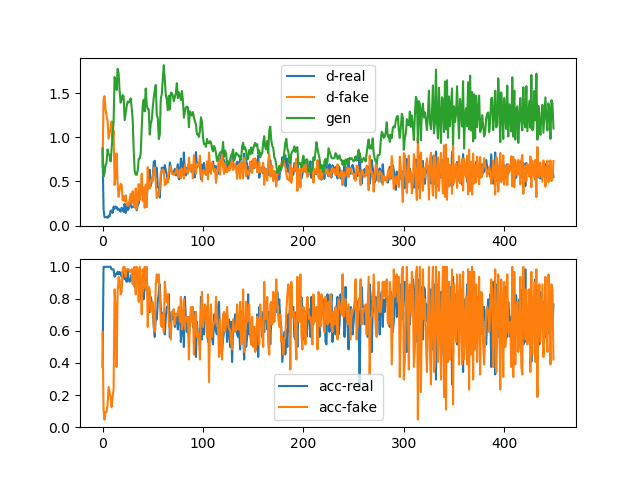
稳定生成对抗网络的损失和准确性折线图
最后,我们可以查看生成的图像样本。注意:我们正在使用反向灰度颜色图生成图像,这意味着普通的白色背景图被反转为白色背景上的黑色图。这是为了使生成的图形更易于查看。
正如我们所料,第 100 个周期之前生成的图像样本质量相对较差。

稳定 GAN 在第 45 个周期生成的 100 张手写数字 8 的图像样本。
第 100 到 300 个周期之间生成的图像样本是合理的,也许是质量最好的。
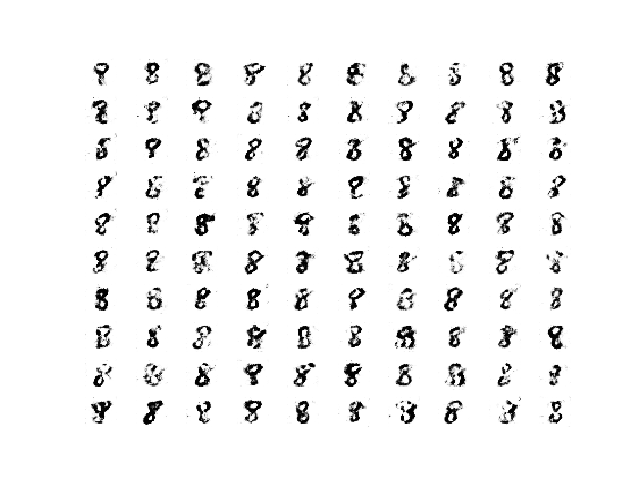
稳定 GAN 在第 180 个周期生成的 100 张手写数字 8 的图像样本。
第 300 个周期之后生成的图像样本仍然是合理的,尽管可能噪声更多,例如背景噪声。
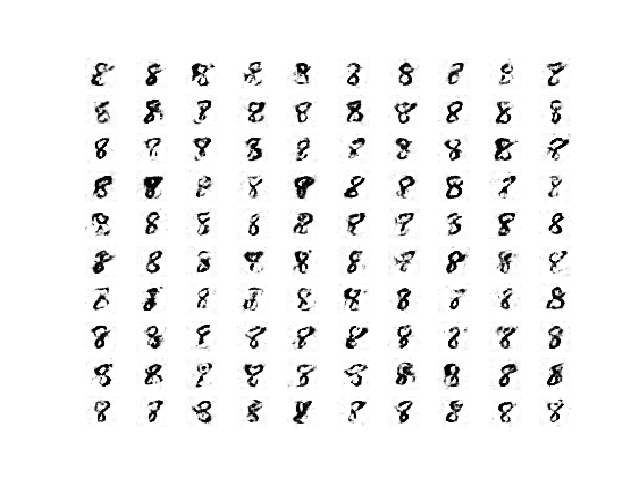
稳定 GAN 在第 450 个周期生成的 100 张手写数字 8 的图像样本。
这些结果很重要,因为它们突出表明,即使在训练过程稳定之后,生成的质量在运行过程中也会发生变化。
超出某个稳定训练点后,更多的训练迭代可能会或可能不会产生更高质量的图像。
我们可以将稳定 GAN 训练的这些观察结果总结如下:
- 真实和假图像的鉴别器损失预期在 0.5 左右。
- 假图像的生成器损失预期在 0.5 到 2.0 之间。
- 真实和假图像的鉴别器准确性预期在 80% 左右。
- 生成器和鉴别器损失的方差预计将保持适中。
- 生成器应在其稳定期间产生最高质量的图像。
- 训练稳定性可能会退化为高方差损失期以及相应较低质量的生成图像。
既然我们有了稳定的 GAN 模型,我们可以修改它来产生一些特定的失败案例。
在 GAN 模型在新问题上训练时,有两种常见的失败案例:模式崩溃和收敛失败。
如何在生成对抗网络中识别模式崩溃
模式崩溃是指生成器模型只能生成一种或一小组不同的结果或模式。
在此,模式是指输出分布,例如,多峰函数是指具有多个峰值或最优值的函数。对于 GAN 生成器模型,模式失败意味着输入潜在空间中的大量点(例如,在许多情况下是 100 维的超球体)会生成一个或一小组生成图像。
模式崩溃,也称为这种情况,是指生成器学会将多个不同的输入 z 值映射到同一个输出点。
— NIPS 2016 教程:生成对抗网络, 2016。
通过查看大量生成的图像样本可以识别模式崩溃。图像将显示多样性低,相同的相同图像或相同的一小组相同图像重复多次。
通过查看模型损失的折线图也可以识别模式崩溃。折线图将显示损失随时间的振荡,尤其是在生成器模型中,因为生成器模型被更新并且从生成一种模式跳到另一种具有不同损失的模式。
我们可以通过多种方式损害我们稳定的 GAN 以使其出现模式崩溃,也许最可靠的方法是直接限制潜在维的大小,迫使模型只生成一小组合理的输出。
具体来说,可以将“*latent_dim*”变量从 100 更改为 1,然后重新运行实验。
|
1 2 |
# 潜在空间的大小 latent_dim = 1 |
完整的代码清单如下。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 |
# 训练一个不稳定的 GAN 以生成手写数字的示例 from os import makedirs from numpy import expand_dims from numpy import zeros from numpy import ones from numpy.random import randn from numpy.random import randint from keras.datasets.mnist import load_data from keras.optimizers import Adam from keras.models import Sequential from keras.layers import Dense from keras.layers import Reshape from keras.layers import Flatten 从 keras.layers 导入 Conv2D from keras.layers import Conv2DTranspose from keras.layers import LeakyReLU from keras.initializers import RandomNormal from matplotlib import pyplot # 定义独立的判别器模型 def define_discriminator(in_shape=(28,28,1)): # 权重初始化 init = RandomNormal(stddev=0.02) # 定义模型 model = Sequential() # 下采样到 14x14 model.add(Conv2D(64, (4,4), strides=(2,2), padding='same', kernel_initializer=init, input_shape=in_shape)) model.add(LeakyReLU(alpha=0.2)) # 下采样到 7x7 model.add(Conv2D(64, (4,4), strides=(2,2), padding='same', kernel_initializer=init)) model.add(LeakyReLU(alpha=0.2)) # 分类器 model.add(Flatten()) model.add(Dense(1, activation='sigmoid')) # 编译模型 opt = Adam(lr=0.0002, beta_1=0.5) model.compile(loss='binary_crossentropy', optimizer=opt, metrics=['accuracy']) return model # 定义独立的生成器模型 def define_generator(latent_dim): # 权重初始化 init = RandomNormal(stddev=0.02) # 定义模型 model = Sequential() # 7x7 图像的基础 n_nodes = 128 * 7 * 7 model.add(Dense(n_nodes, kernel_initializer=init, input_dim=latent_dim)) model.add(LeakyReLU(alpha=0.2)) model.add(Reshape((7, 7, 128))) # 上采样到 14x14 model.add(Conv2DTranspose(128, (4,4), strides=(2,2), padding='same', kernel_initializer=init)) model.add(LeakyReLU(alpha=0.2)) # 上采样到 28x28 model.add(Conv2DTranspose(128, (4,4), strides=(2,2), padding='same', kernel_initializer=init)) model.add(LeakyReLU(alpha=0.2)) # 输出 28x28x1 model.add(Conv2D(1, (7,7), activation='tanh', padding='same', kernel_initializer=init)) return model # 定义组合的生成器和判别器模型,用于更新生成器 def define_gan(generator, discriminator): # 使判别器中的权重不可训练 discriminator.trainable = False # 连接它们 model = Sequential() # 添加生成器 model.add(generator) # 添加判别器 model.add(discriminator) # 编译模型 opt = Adam(lr=0.0002, beta_1=0.5) model.compile(loss='binary_crossentropy', optimizer=opt) return model # 加载mnist图像 def load_real_samples(): # 加载数据集 (trainX, trainy), (_, _) = load_data() # 扩展到3D,例如添加通道 X = expand_dims(trainX, axis=-1) # 选择给定类别的所有样本 selected_ix = trainy == 8 X = X[selected_ix] # 从整数转换为浮点数 X = X.astype('float32') # 从 [0,255] 缩放到 [-1,1] X = (X - 127.5) / 127.5 return X # # 选择真实样本 def generate_real_samples(dataset, n_samples): # 选择随机实例 ix = randint(0, dataset.shape[0], n_samples) # 选择图像 X = dataset[ix] # 生成类别标签 y = ones((n_samples, 1)) 返回 X, y # 在潜在空间中生成点作为生成器的输入 def generate_latent_points(latent_dim, n_samples): # 在潜在空间中生成点 x_input = randn(latent_dim * n_samples) # 重塑为网络的输入批次 x_input = x_input.reshape(n_samples, latent_dim) return x_input # 使用生成器生成 n 个假示例,并带有类别标签 def generate_fake_samples(generator, latent_dim, n_samples): # 在潜在空间中生成点 x_input = generate_latent_points(latent_dim, n_samples) # 预测输出 X = generator.predict(x_input) # 创建类别标签 y = zeros((n_samples, 1)) 返回 X, y # 生成样本并保存为图,并保存模型 def summarize_performance(step, g_model, latent_dim, n_samples=100): # 准备伪示例 X, _ = generate_fake_samples(g_model, latent_dim, n_samples) # 将范围从[-1,1]缩放到[0,1] X = (X + 1) / 2.0 # 绘制图像 for i in range(10 * 10): # 定义子图 pyplot.subplot(10, 10, 1 + i) # 关闭轴线 pyplot.axis('off') # 绘制原始像素数据 pyplot.imshow(X[i, :, :, 0], cmap='gray_r') # 保存图到文件 pyplot.savefig('results_collapse/generated_plot_%03d.png' % (step+1)) pyplot.close() # 保存生成器模型 g_model.save('results_collapse/model_%03d.h5' % (step+1)) # 创建GAN损失的折线图并保存到文件 def plot_history(d1_hist, d2_hist, g_hist, a1_hist, a2_hist): # 绘制损失 pyplot.subplot(2, 1, 1) pyplot.plot(d1_hist, label='d-real') pyplot.plot(d2_hist, label='d-fake') pyplot.plot(g_hist, label='gen') pyplot.legend() # 绘制判别器准确率 pyplot.subplot(2, 1, 2) pyplot.plot(a1_hist, label='acc-real') pyplot.plot(a2_hist, label='acc-fake') pyplot.legend() # 保存图到文件 pyplot.savefig('results_collapse/plot_line_plot_loss.png') pyplot.close() # 训练生成器和判别器 def train(g_model, d_model, gan_model, dataset, latent_dim, n_epochs=10, n_batch=128): # 计算每个周期的批次数 bat_per_epo = int(dataset.shape[0] / n_batch) # 根据批次和周期计算总迭代次数 n_steps = bat_per_epo * n_epochs # 计算半个批次中的样本数 half_batch = int(n_batch / 2) # 准备用于存储每次迭代统计信息的列表 d1_hist, d2_hist, g_hist, a1_hist, a2_hist = list(), list(), list(), list(), list() # 手动枚举 epoch for i in range(n_steps): # 获取随机选择的“真实”样本 X_real, y_real = generate_real_samples(dataset, half_batch) # 更新判别器模型权重 d_loss1, d_acc1 = d_model.train_on_batch(X_real, y_real) # 生成“假”示例 X_fake, y_fake = generate_fake_samples(g_model, latent_dim, half_batch) # 更新判别器模型权重 d_loss2, d_acc2 = d_model.train_on_batch(X_fake, y_fake) # 准备潜在空间中的点作为生成器的输入 X_gan = generate_latent_points(latent_dim, n_batch) # 为伪样本创建反转标签 y_gan = ones((n_batch, 1)) # 通过判别器的误差更新生成器 g_loss = gan_model.train_on_batch(X_gan, y_gan) # 总结此批次的损失 print('>%d, d1=%.3f, d2=%.3f g=%.3f, a1=%d, a2=%d' % (i+1, d_loss1, d_loss2, g_loss, int(100*d_acc1), int(100*d_acc2))) # 记录历史 d1_hist.append(d_loss1) d2_hist.append(d_loss2) g_hist.append(g_loss) a1_hist.append(d_acc1) a2_hist.append(d_acc2) # 每“个周期”评估模型性能 if (i+1) % bat_per_epo == 0: summarize_performance(i, g_model, latent_dim) plot_history(d1_hist, d2_hist, g_hist, a1_hist, a2_hist) # 为结果创建文件夹 makedirs('results_collapse', exist_ok=True) # 潜在空间的大小 latent_dim = 1 # 创建判别器 discriminator = define_discriminator() # 创建生成器 generator = define_generator(latent_dim) # 创建GAN gan_model = define_gan(generator, discriminator) # 加载图像数据 dataset = load_real_samples() print(dataset.shape) # 训练模型 train(generator, discriminator, gan_model, dataset, latent_dim) |
运行示例将像以前一样报告每次训练步骤的损失和准确性。
在这种情况下,鉴别器的损失在合理的范围内,但生成器的损失上下波动。鉴别器的准确性也显示出更高的值,许多都在 100% 左右,这意味着对于许多批次,它在识别真实或虚假样本方面具有完美的技能,这对图像质量或多样性来说是个坏兆头。
|
1 2 3 4 5 6 7 8 9 10 11 |
>1, d1=0.963, d2=0.699 g=0.614, a1=28, a2=54 >2, d1=0.185, d2=5.084 g=0.097, a1=96, a2=0 >3, d1=0.088, d2=4.861 g=0.065, a1=100, a2=0 >4, d1=0.077, d2=4.202 g=0.090, a1=100, a2=0 >5, d1=0.062, d2=3.533 g=0.128, a1=100, a2=0 ... >446, d1=0.277, d2=0.261 g=0.684, a1=95, a2=100 >447, d1=0.201, d2=0.247 g=0.713, a1=96, a2=100 >448, d1=0.285, d2=0.285 g=0.728, a1=89, a2=100 >449, d1=0.351, d2=0.467 g=1.184, a1=92, a2=81 >450, d1=0.492, d2=0.388 g=1.351, a1=76, a2=100 |
创建并保存包含学习曲线和准确性折线图的图形。
在顶部子图中,我们可以看到生成器(绿色)的损失随时间在合理值和高值之间振荡,周期约为 25 个模型更新(批次)。我们还可以看到真实样本和假样本的鉴别器损失(橙色和蓝色)有一些小的振荡。
在底部子图中,我们可以看到鉴别器在整个运行过程中识别假图像的分类准确性仍然很高。这表明生成器在以某种一致的方式生成样本方面很差,使得鉴别器很容易识别假图像。
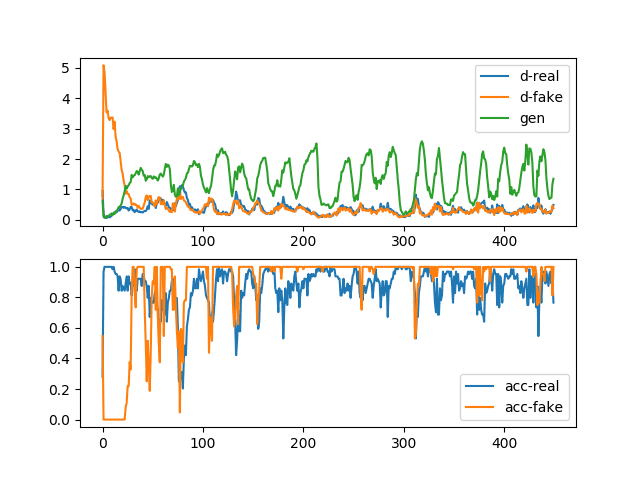
具有模式崩溃的生成对抗网络的损失和准确性折线图
查看生成的图像显示了模式崩溃的预期特征,即无论潜在空间中的输入点如何,都会生成许多相同的图像。碰巧我们已经将潜在空间的维度更改为非常小,以强制产生这种效果。
我选择了一个生成的图像示例来使其更清晰。图像中似乎只有几种数字 8 的类型,一种向左倾斜,一种向右倾斜,一种直立且模糊。
我在下图中用框标出了相似的示例,以使其更清晰。
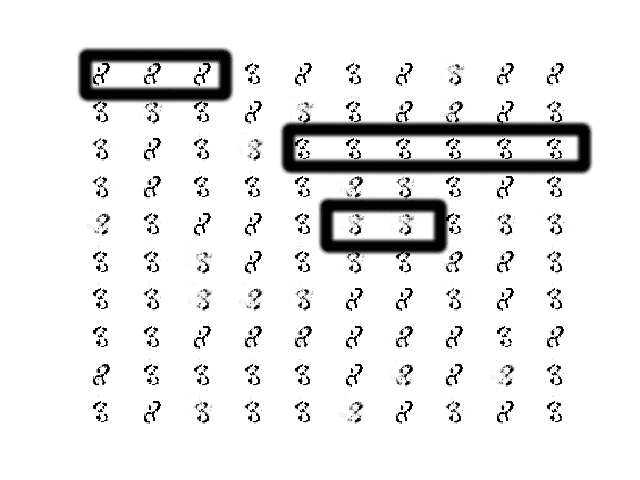
遭受模式崩溃的 GAN 在第 315 个周期生成的 100 张手写数字 8 的图像样本。
根据 DCGAN 模型架构和训练配置的发现,在训练期间模式崩溃不太常见。
总而言之,您可以按如下方式识别模式崩溃:
- 生成器(可能还有鉴别器)的损失预期会随时间振荡。
- 生成器模型应从潜在空间的点生成相同的输出图像。
如何识别生成对抗网络中的收敛失败
在训练 GAN 时,最常见的失败可能是未能收敛。
通常,神经网络在训练过程中模型损失未能稳定下来时会失败。在 GAN 的情况下,未能收敛是指未能找到鉴别器和生成器之间的平衡。
识别这种失败类型的可能方式是鉴别器的损失降至零或接近零。在某些情况下,生成器的损失也可能在此期间上升并持续上升。
这种类型的损失最常由生成器输出垃圾图像引起,鉴别器可以轻松识别这些图像。
这种类型的失败可能发生在运行开始时并持续整个训练过程,此时您应该停止训练过程。对于一些不稳定的 GAN,GAN 可能会在许多批次更新或甚至许多周期内陷入这种失败模式,然后恢复。
有许多方法可以使我们稳定的 GAN 出现收敛失败,例如将一个或两个模型更改为具有不足的容量,将Adam 优化算法更改为过于激进,以及在模型中使用非常大或非常小的内核大小。
在此示例中,我们将更新示例以在更新鉴别器时合并真实和假样本。这个简单的更改将导致模型未能收敛。
这个更改就像使用 vstack() NumPy 函数组合真实和假样本,然后调用 train_on_batch() 函数来更新鉴别器模型一样简单。结果也是单一的损失和准确性分数,这意味着模型性能的报告也必须更新。
为完整起见,下面提供了包含这些更改的完整代码列表。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 |
# 训练一个不稳定的 GAN 以生成手写数字的示例 from os import makedirs from numpy import expand_dims from numpy import zeros from numpy import ones from numpy import vstack from numpy.random import randn from numpy.random import randint from keras.datasets.mnist import load_data from keras.optimizers import Adam from keras.models import Sequential from keras.layers import Dense from keras.layers import Reshape from keras.layers import Flatten 从 keras.layers 导入 Conv2D from keras.layers import Conv2DTranspose from keras.layers import LeakyReLU from keras.initializers import RandomNormal from matplotlib import pyplot # 定义独立的判别器模型 def define_discriminator(in_shape=(28,28,1)): # 权重初始化 init = RandomNormal(stddev=0.02) # 定义模型 model = Sequential() # 下采样到 14x14 model.add(Conv2D(64, (4,4), strides=(2,2), padding='same', kernel_initializer=init, input_shape=in_shape)) model.add(LeakyReLU(alpha=0.2)) # 下采样到 7x7 model.add(Conv2D(64, (4,4), strides=(2,2), padding='same', kernel_initializer=init)) model.add(LeakyReLU(alpha=0.2)) # 分类器 model.add(Flatten()) model.add(Dense(1, activation='sigmoid')) # 编译模型 opt = Adam(lr=0.0002, beta_1=0.5) model.compile(loss='binary_crossentropy', optimizer=opt, metrics=['accuracy']) return model # 定义独立的生成器模型 def define_generator(latent_dim): # 权重初始化 init = RandomNormal(stddev=0.02) # 定义模型 model = Sequential() # 7x7 图像的基础 n_nodes = 128 * 7 * 7 model.add(Dense(n_nodes, kernel_initializer=init, input_dim=latent_dim)) model.add(LeakyReLU(alpha=0.2)) model.add(Reshape((7, 7, 128))) # 上采样到 14x14 model.add(Conv2DTranspose(128, (4,4), strides=(2,2), padding='same', kernel_initializer=init)) model.add(LeakyReLU(alpha=0.2)) # 上采样到 28x28 model.add(Conv2DTranspose(128, (4,4), strides=(2,2), padding='same', kernel_initializer=init)) model.add(LeakyReLU(alpha=0.2)) # 输出 28x28x1 model.add(Conv2D(1, (7,7), activation='tanh', padding='same', kernel_initializer=init)) return model # 定义组合的生成器和判别器模型,用于更新生成器 def define_gan(generator, discriminator): # 使判别器中的权重不可训练 discriminator.trainable = False # 连接它们 model = Sequential() # 添加生成器 model.add(generator) # 添加判别器 model.add(discriminator) # 编译模型 opt = Adam(lr=0.0002, beta_1=0.5) model.compile(loss='binary_crossentropy', optimizer=opt) return model # 加载mnist图像 def load_real_samples(): # 加载数据集 (trainX, trainy), (_, _) = load_data() # 扩展到3D,例如添加通道 X = expand_dims(trainX, axis=-1) # 选择给定类别的所有样本 selected_ix = trainy == 8 X = X[selected_ix] # 从整数转换为浮点数 X = X.astype('float32') # 从 [0,255] 缩放到 [-1,1] X = (X - 127.5) / 127.5 return X # # 选择真实样本 def generate_real_samples(dataset, n_samples): # 选择随机实例 ix = randint(0, dataset.shape[0], n_samples) # 选择图像 X = dataset[ix] # 生成类别标签 y = ones((n_samples, 1)) 返回 X, y # 在潜在空间中生成点作为生成器的输入 def generate_latent_points(latent_dim, n_samples): # 在潜在空间中生成点 x_input = randn(latent_dim * n_samples) # 重塑为网络的输入批次 x_input = x_input.reshape(n_samples, latent_dim) return x_input # 使用生成器生成 n 个假示例,并带有类别标签 def generate_fake_samples(generator, latent_dim, n_samples): # 在潜在空间中生成点 x_input = generate_latent_points(latent_dim, n_samples) # 预测输出 X = generator.predict(x_input) # 创建类别标签 y = zeros((n_samples, 1)) 返回 X, y # 生成样本并保存为图,并保存模型 def summarize_performance(step, g_model, latent_dim, n_samples=100): # 准备伪示例 X, _ = generate_fake_samples(g_model, latent_dim, n_samples) # 将范围从[-1,1]缩放到[0,1] X = (X + 1) / 2.0 # 绘制图像 for i in range(10 * 10): # 定义子图 pyplot.subplot(10, 10, 1 + i) # 关闭轴线 pyplot.axis('off') # 绘制原始像素数据 pyplot.imshow(X[i, :, :, 0], cmap='gray_r') # 保存图到文件 pyplot.savefig('results_convergence/generated_plot_%03d.png' % (step+1)) pyplot.close() # 保存生成器模型 g_model.save('results_convergence/model_%03d.h5' % (step+1)) # 创建GAN损失的折线图并保存到文件 def plot_history(d_hist, g_hist, a_hist): # 绘制损失 pyplot.subplot(2, 1, 1) pyplot.plot(d_hist, label='dis') pyplot.plot(g_hist, label='gen') pyplot.legend() # 绘制判别器准确率 pyplot.subplot(2, 1, 2) pyplot.plot(a_hist, label='acc') pyplot.legend() # 保存图到文件 pyplot.savefig('results_convergence/plot_line_plot_loss.png') pyplot.close() # 训练生成器和判别器 def train(g_model, d_model, gan_model, dataset, latent_dim, n_epochs=10, n_batch=128): # 计算每个周期的批次数 bat_per_epo = int(dataset.shape[0] / n_batch) # 根据批次和周期计算总迭代次数 n_steps = bat_per_epo * n_epochs # 计算半个批次中的样本数 half_batch = int(n_batch / 2) # 准备用于存储每次迭代统计信息的列表 d_hist, g_hist, a_hist = list(), list(), list() # 手动枚举 epoch for i in range(n_steps): # 获取随机选择的“真实”样本 X_real, y_real = generate_real_samples(dataset, half_batch) # 生成“假”示例 X_fake, y_fake = generate_fake_samples(g_model, latent_dim, half_batch) # 合并成一个批次 X, y = vstack((X_real, X_fake)), vstack((y_real, y_fake)) # 更新判别器模型权重 d_loss, d_acc = d_model.train_on_batch(X, y) # 准备潜在空间中的点作为生成器的输入 X_gan = generate_latent_points(latent_dim, n_batch) # 为伪样本创建反转标签 y_gan = ones((n_batch, 1)) # 通过判别器的误差更新生成器 g_loss = gan_model.train_on_batch(X_gan, y_gan) # 总结此批次的损失 print('>%d, d=%.3f, g=%.3f, a=%d' % (i+1, d_loss, g_loss, int(100*d_acc))) # 记录历史 d_hist.append(d_loss) g_hist.append(g_loss) a_hist.append(d_acc) # 每“个周期”评估模型性能 if (i+1) % bat_per_epo == 0: summarize_performance(i, g_model, latent_dim) plot_history(d_hist, g_hist, a_hist) # 为结果创建文件夹 makedirs('results_convergence', exist_ok=True) # 潜在空间的大小 latent_dim = 50 # 创建判别器 discriminator = define_discriminator() # 创建生成器 generator = define_generator(latent_dim) # 创建GAN gan_model = define_gan(generator, discriminator) # 加载图像数据 dataset = load_real_samples() print(dataset.shape) # 训练模型 train(generator, discriminator, gan_model, dataset, latent_dim) |
运行示例会报告每次模型更新时的损失和准确性。
这种类型失败的一个明显迹象是鉴别器损失迅速下降到零附近,并保持在那里。
这正是我们在本例中看到的情况。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
>1, d=0.514, g=0.969, a=80 >2, d=0.475, g=0.395, a=74 >3, d=0.452, g=0.223, a=69 >4, d=0.302, g=0.220, a=85 >5, d=0.177, g=0.195, a=100 >6, d=0.122, g=0.200, a=100 >7, d=0.088, g=0.179, a=100 >8, d=0.075, g=0.159, a=100 >9, d=0.071, g=0.167, a=100 >10, d=0.102, g=0.127, a=100 ... >446, d=0.000, g=0.001, a=100 >447, d=0.000, g=0.001, a=100 >448, d=0.000, g=0.001, a=100 >449, d=0.000, g=0.001, a=100 >450, d=0.000, g=0.001, a=100 |
创建了学习曲线和分类准确性的图。
顶部子图显示了鉴别器(蓝色)和生成器(橙色)的损失,并清楚地显示了前 20 到 30 次迭代中两者值均下降到零附近,并在其余运行中保持在那里。
底部子图显示了在此期间鉴别器分类准确性保持在 100%,这意味着模型在识别真实和虚假图像方面是完美的。预期的是,假图像有一些使其易于鉴别器识别的特征。
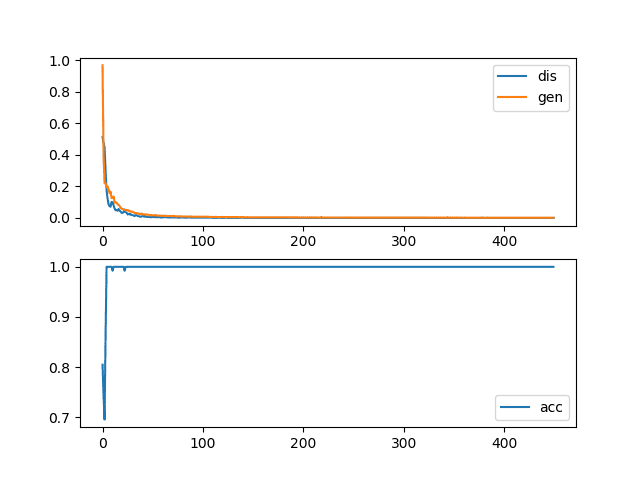
具有收敛失败的生成对抗网络的损失和准确性折线图
最后,查看生成的图像样本使鉴别器如此成功的原因更加清楚。
每个周期的生成图像样本质量都非常低,显示出静态,可能背景中有一个模糊的数字 8。

通过组合鉴别器更新导致收敛失败的 GAN 在第 450 个周期生成的 100 张手写数字 8 的图像样本。
看到另一种失败的例子很有用。
在这种情况下,可以修改 Adam 优化算法的配置以使用默认值,这反过来会使模型的更新变得激进,并导致训练过程在两个模型之间找不到平衡点。
例如,鉴别器可以如下编译:
|
1 2 3 |
... # 编译模型 model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy']) |
以及复合 GAN 模型可以如下编译:
|
1 2 3 |
... # 编译模型 model.compile(loss='binary_crossentropy', optimizer='adam') |
完整的代码清单如下。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 |
# 训练一个不稳定的 GAN 以生成手写数字的示例 from os import makedirs from numpy import expand_dims from numpy import zeros from numpy import ones from numpy.random import randn from numpy.random import randint from keras.datasets.mnist import load_data from keras.models import Sequential from keras.layers import Dense from keras.layers import Reshape from keras.layers import Flatten 从 keras.layers 导入 Conv2D from keras.layers import Conv2DTranspose from keras.layers import LeakyReLU from keras.initializers import RandomNormal from matplotlib import pyplot # 定义独立的判别器模型 def define_discriminator(in_shape=(28,28,1)): # 权重初始化 init = RandomNormal(stddev=0.02) # 定义模型 model = Sequential() # 下采样到 14x14 model.add(Conv2D(64, (4,4), strides=(2,2), padding='same', kernel_initializer=init, input_shape=in_shape)) model.add(LeakyReLU(alpha=0.2)) # 下采样到 7x7 model.add(Conv2D(64, (4,4), strides=(2,2), padding='same', kernel_initializer=init)) model.add(LeakyReLU(alpha=0.2)) # 分类器 model.add(Flatten()) model.add(Dense(1, activation='sigmoid')) # 编译模型 model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy']) return model # 定义独立的生成器模型 def define_generator(latent_dim): # 权重初始化 init = RandomNormal(stddev=0.02) # 定义模型 model = Sequential() # 7x7 图像的基础 n_nodes = 128 * 7 * 7 model.add(Dense(n_nodes, kernel_initializer=init, input_dim=latent_dim)) model.add(LeakyReLU(alpha=0.2)) model.add(Reshape((7, 7, 128))) # 上采样到 14x14 model.add(Conv2DTranspose(128, (4,4), strides=(2,2), padding='same', kernel_initializer=init)) model.add(LeakyReLU(alpha=0.2)) # 上采样到 28x28 model.add(Conv2DTranspose(128, (4,4), strides=(2,2), padding='same', kernel_initializer=init)) model.add(LeakyReLU(alpha=0.2)) # 输出 28x28x1 model.add(Conv2D(1, (7,7), activation='tanh', padding='same', kernel_initializer=init)) return model # 定义组合的生成器和判别器模型,用于更新生成器 def define_gan(generator, discriminator): # 使判别器中的权重不可训练 discriminator.trainable = False # 连接它们 model = Sequential() # 添加生成器 model.add(generator) # 添加判别器 model.add(discriminator) # 编译模型 model.compile(loss='binary_crossentropy', optimizer='adam') return model # 加载mnist图像 def load_real_samples(): # 加载数据集 (trainX, trainy), (_, _) = load_data() # 扩展到3D,例如添加通道 X = expand_dims(trainX, axis=-1) # 选择给定类别的所有样本 selected_ix = trainy == 8 X = X[selected_ix] # 从整数转换为浮点数 X = X.astype('float32') # 从 [0,255] 缩放到 [-1,1] X = (X - 127.5) / 127.5 return X # 选择真实样本 def generate_real_samples(dataset, n_samples): # 选择随机实例 ix = randint(0, dataset.shape[0], n_samples) # 选择图像 X = dataset[ix] # 生成类别标签 y = ones((n_samples, 1)) 返回 X, y # 在潜在空间中生成点作为生成器的输入 def generate_latent_points(latent_dim, n_samples): # 在潜在空间中生成点 x_input = randn(latent_dim * n_samples) # 重塑为网络的输入批次 x_input = x_input.reshape(n_samples, latent_dim) return x_input # 使用生成器生成 n 个假示例,并带有类别标签 def generate_fake_samples(generator, latent_dim, n_samples): # 在潜在空间中生成点 x_input = generate_latent_points(latent_dim, n_samples) # 预测输出 X = generator.predict(x_input) # 创建类别标签 y = zeros((n_samples, 1)) 返回 X, y # 生成样本并保存为图,并保存模型 def summarize_performance(step, g_model, latent_dim, n_samples=100): # 准备伪示例 X, _ = generate_fake_samples(g_model, latent_dim, n_samples) # 将范围从[-1,1]缩放到[0,1] X = (X + 1) / 2.0 # 绘制图像 for i in range(10 * 10): # 定义子图 pyplot.subplot(10, 10, 1 + i) # 关闭轴线 pyplot.axis('off') # 绘制原始像素数据 pyplot.imshow(X[i, :, :, 0], cmap='gray_r') # 保存图到文件 pyplot.savefig('results_opt/generated_plot_%03d.png' % (step+1)) pyplot.close() # 保存生成器模型 g_model.save('results_opt/model_%03d.h5' % (step+1)) # 创建GAN损失的折线图并保存到文件 def plot_history(d1_hist, d2_hist, g_hist, a1_hist, a2_hist): # 绘制损失 pyplot.subplot(2, 1, 1) pyplot.plot(d1_hist, label='d-real') pyplot.plot(d2_hist, label='d-fake') pyplot.plot(g_hist, label='gen') pyplot.legend() # 绘制判别器准确率 pyplot.subplot(2, 1, 2) pyplot.plot(a1_hist, label='acc-real') pyplot.plot(a2_hist, label='acc-fake') pyplot.legend() # 保存图到文件 pyplot.savefig('results_opt/plot_line_plot_loss.png') pyplot.close() # 训练生成器和判别器 def train(g_model, d_model, gan_model, dataset, latent_dim, n_epochs=10, n_batch=128): # 计算每个周期的批次数 bat_per_epo = int(dataset.shape[0] / n_batch) # 根据批次和周期计算总迭代次数 n_steps = bat_per_epo * n_epochs # 计算半个批次中的样本数 half_batch = int(n_batch / 2) # 准备用于存储每次迭代统计信息的列表 d1_hist, d2_hist, g_hist, a1_hist, a2_hist = list(), list(), list(), list(), list() # 手动枚举 epoch for i in range(n_steps): # 获取随机选择的“真实”样本 X_real, y_real = generate_real_samples(dataset, half_batch) # 更新判别器模型权重 d_loss1, d_acc1 = d_model.train_on_batch(X_real, y_real) # 生成“假”示例 X_fake, y_fake = generate_fake_samples(g_model, latent_dim, half_batch) # 更新判别器模型权重 d_loss2, d_acc2 = d_model.train_on_batch(X_fake, y_fake) # 准备潜在空间中的点作为生成器的输入 X_gan = generate_latent_points(latent_dim, n_batch) # 为伪样本创建反转标签 y_gan = ones((n_batch, 1)) # 通过判别器的误差更新生成器 g_loss = gan_model.train_on_batch(X_gan, y_gan) # 总结此批次的损失 print('>%d, d1=%.3f, d2=%.3f g=%.3f, a1=%d, a2=%d' % (i+1, d_loss1, d_loss2, g_loss, int(100*d_acc1), int(100*d_acc2))) # 记录历史 d1_hist.append(d_loss1) d2_hist.append(d_loss2) g_hist.append(g_loss) a1_hist.append(d_acc1) a2_hist.append(d_acc2) # 每“个周期”评估模型性能 if (i+1) % bat_per_epo == 0: summarize_performance(i, g_model, latent_dim) plot_history(d1_hist, d2_hist, g_hist, a1_hist, a2_hist) # 为结果创建文件夹 makedirs('results_opt', exist_ok=True) # 潜在空间的大小 latent_dim = 50 # 创建判别器 discriminator = define_discriminator() # 创建生成器 generator = define_generator(latent_dim) # 创建GAN gan_model = define_gan(generator, discriminator) # 加载图像数据 dataset = load_real_samples() print(dataset.shape) # 训练模型 train(generator, discriminator, gan_model, dataset, latent_dim) |
运行示例会在训练过程中报告每一步的损失和准确性,与之前一样。
正如我们所预期的,鉴别器的损失迅速下降到接近零的值并保持在那里,而鉴别器在真实和虚假样本上的分类准确性保持在 100%。
|
1 2 3 4 5 6 7 8 9 10 11 |
>1, d1=0.728, d2=0.902 g=0.763, a1=54, a2=12 >2, d1=0.001, d2=4.509 g=0.033, a1=100, a2=0 >3, d1=0.000, d2=0.486 g=0.542, a1=100, a2=76 >4, d1=0.000, d2=0.446 g=0.733, a1=100, a2=82 >5, d1=0.002, d2=0.855 g=0.649, a1=100, a2=46 ... >446, d1=0.000, d2=0.000 g=10.410, a1=100, a2=100 >447, d1=0.000, d2=0.000 g=10.414, a1=100, a2=100 >448, d1=0.000, d2=0.000 g=10.419, a1=100, a2=100 >449, d1=0.000, d2=0.000 g=10.424, a1=100, a2=100 >450, d1=0.000, d2=0.000 g=10.427, a1=100, a2=100 |
创建了使用此单一更改训练模型的学习曲线和准确性图。
该图显示此更改导致鉴别器的损失急剧下降到接近零的值并保持在那里。此案例的一个重要区别是生成器的损失迅速上升并在整个训练过程中继续上升。
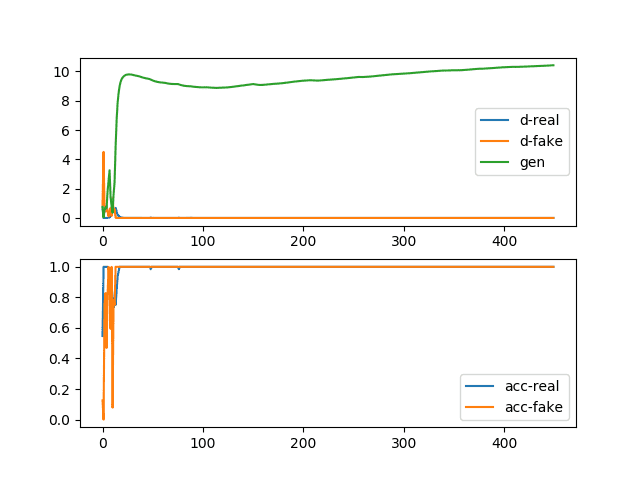
由于激进优化导致的收敛失败的生成对抗网络的损失和准确性折线图
我们可以按如下方式审查收敛失败的特性:
- 鉴别器的损失预计会迅速下降到接近零的值,并在训练期间保持在该值。
- 生成器的损失预计在训练期间会下降到零或持续下降。
- 生成器预计会产生极低质量的图像,很容易被鉴别器识别为伪造。
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
论文
- 生成对抗网络, 2014.
- 教程:生成对抗网络,NIPS, 2016.
- 使用深度卷积生成对抗网络的无监督表征学习, 2015.
文章
总结
在本教程中,您通过回顾生成的图像示例以及训练期间记录的指标图,学习了如何识别稳定和不稳定的 GAN 训练。
具体来说,你学到了:
- 如何通过查看生成器和判别器随时间的损失来识别稳定的GAN训练过程。
- 如何通过查看学习曲线和生成的图像来识别模式崩溃。
- 如何通过查看生成器和判别器随时间的损失的学习曲线来识别收敛失败。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。



Jason,又一篇好文章。
我有两个小问题
1.在关于收敛失败的章节中,您提到的第一个可能出错的方法是堆叠真实和虚假样本。
我非常不理解为什么训练不同类型的样本会导致这种失败,尤其是在我按照另一篇文章 [https://machinelearning.org.cn/how-to-develop-a-generative-adversarial-network-for-an-mnist-handwritten-digits-from-scratch-in-keras/] 操作之后。
在上面链接的文章中,您演示了堆叠操作,并且结果很好(我尝试后也是如此)。
2. 也许和第一个问题一样(在我尝试上面链接的文章时也发生了)。但当我尝试在您的原始代码中添加 BatchNormalization 层时,出现了一个奇怪的现象,导致了收敛失败。
看似无害的 BatchNormalization 为什么会导致这种失败?
感谢您阅读这篇冗长的提问。期待您的回复。
此致。
顺便说一句,我在 Kaggle 上尝试了您的作品。链接是: https://www.kaggle.com/jinyongnan/the-basic-2dgans
版本 3 是带有 BatchNormalization 的版本,版本 4 是没有的版本。
好问题。
在训练期间不堆叠真实/虚假图像通常更好。也许可以尝试这两种方法,看看哪种最适合您的问题。
模型非常敏感,微小的改动都可能导致失败。仔细测试改动,并确定原因(为什么)是非常困难的。
您知道任何 papers 或其他来源更深入地分析为什么在训练期间最好不要堆叠真实和虚假图像吗?这对我来说也非常不直观,我想了解更多关于为什么会这样。
不是真的,就像大多数 GAN 的经验法则一样,它是经验性的/默会知识。
这可能有关
https://github.com/soumith/ganhacks
这似乎与批归一化有关。我的初步尝试表明,如果您使用批归一化,并且用混合的真实/虚假批次训练鉴别器,它可能会遇到问题。如果您训练的批次仅包含真实数据,然后仅包含虚假数据,您仍然可能会遇到问题,但会发生在更晚的 epoch。此外,如果您确实遇到了问题(即损失变为 0 或无穷大),您可以停止训练,并从模型仍然正常的最后一个保存点加载参数。当您继续训练时,您可能不会陷入同样的困境。
观察得很棒!
抱歉我只能在这里提问,我非常感谢您的文章,我有 2 个问题
1.在生成器和鉴别器的训练过程中,是否应该设置优化器的学习率衰减?我读过一些代码,发现他们没有设置,但这是许多其他深度学习任务中的常见设置。
2.我使用 pytorch 训练我的 GAN 模型,在生成器训练过程中,是否应该使用 model.eval() 来冻结鉴别器?在训练鉴别器时,对于生成器是否也应该采取相同的处理?
请原谅我糟糕的英语,我期待您的回复!
嗨 John……您可能想从这里开始
https://machinelearning.org.cn/start-here/#gans
如果您有兴趣,我测试了您的稳定架构并做了一些修改
(Dis 是鉴别器,gen 是生成器)
Dis 中的平均池化,gen 中的上采样,步长 = 1x1
https://drive.google.com/file/d/1K8CFI1X3CORXBvXKOUaCAI8L0aKobLpa/view?usp=sharing
(我没有发现训练 MNIST 数据集后 gen 输出质量的变化,但在复杂数据上,它会给出更好的结果,而不是步长 = 2x2)
++ 过滤器大小 = 3x3
https://drive.google.com/file/d/1nuIKvTleXNBtDdOgL4UQ46YA7I-RJOk9/view?usp=sharing
(图像生成质量略差,但每个人都建议使用奇数过滤器大小)
++ Dis 中的过滤器数量为 32-64,gen 中的过滤器数量为 64-32,而不是 Dis 中的 64-64 和 gen 中的 128-128
https://drive.google.com/file/d/1QwaUbTw9Fs3hGpYhLE7zTJyJCnmRBKyk/view?usp=sharing
(训练后生成的图像相同,但使用镜像生成器和鉴别器最大化网络训练稳定性。您在简单的像 MNIST 这样的数据集上不会注意到这一点,但我见过训练因为我使用非镜像 GAN 而在复杂的 3D 数据上崩溃)
++ Dis 学习率 x2
https://drive.google.com/file/d/1IkUuKZNlBCiNJqKkAWHtDvQyw-Tvomlg/view?usp=sharing
(我见过它有时被使用,但不知道为什么。我测试了 x3,但 x2 上的损失和训练准确性更平滑)
比较(之前/之后)
迭代 45
之前 – https://drive.google.com/open?id=1uaiSp_OCIlcV79wYfybDMJR3g3xR7O4C
之后 – https://drive.google.com/open?id=1Mu6BInIVnC17jigiTh4L1aOqAnieeitv
迭代 450
之前 – https://drive.google.com/open?id=1Bspoo7BwuzyaA7CCYVig1d2qfTyNrHSa
之后 – https://drive.google.com/open?id=1vwmtinHEGDfkrB-TTU8-XhtVrb30jEPK
抱歉我的英语不好
一点也不,我们在这里想要的是结果,而不是优秀的英语🙂
感谢分享!
你好,
首先,感谢您的文章!
我有一个问题。在训练了我的模型 500 个 epoch 后,acc_real 和 acc_fake 仍然为 0。训练期间没有任何变化,生成的图像表明模型未能收敛。鉴别器和生成器的损失在波动,但大部分保持在 0。您能解释一下这是怎么回事以及如何解决吗?
通常,GAN 模型不会收敛。我在这里解释更多
https://machinelearning.org.cn/faq/single-faq/why-is-my-gan-not-converging
感谢您的建议。
通过删除标签平滑,我修复了这个问题。损失和准确率正在如预期般波动。但是,当我查看生成的图像时,图像似乎在改进,然后又回到了噪声图像,并在训练过程中重复多次。您能帮我弄清楚为什么会发生这种情况吗?
干得好。
是的,您必须在训练过程中频繁保存模型,然后通过生成的图像进行事后评估,以便选择最终模型。
这真是太棒了。谢谢,Jason
谢谢,很高兴它能帮到你!
嗨 Jason。感谢这篇精彩的文章!
我正在训练一个 pix2pix 模型,我的真实和虚假样本上的鉴别器损失在几次迭代后在 0.3 左右波动,而生成器损失却在下降。您知道这表明什么吗?
如果您有时间,请看一下我的图表。
https://drive.google.com/file/d/16NSq5FdKRyIm3oxrVXCXL1-yU9LefGRS/view?usp=sharing
不行。
也许可以尝试这里的一些对策
https://machinelearning.org.cn/how-to-code-generative-adversarial-network-hacks/
嗨 Jason,我修改了您的 pix2pix 实现,因此大部分技巧都已经实现了。我使用 mae 和 log loss 作为生成器。我可能错了,但似乎剩余的差异 (20x20) 相对于输入大小 (512,512) 太小了。因此,损失非常小,鉴别器和生成器的损失无法再降低。您对如何让网络更好地学习低级特征有什么建议吗?
干得好!
目前没有,通过受控实验探索想法。
嗨,Jason!
一如既往的出色工作!我在目前训练的 GAN 时遇到一个小问题,很想听听您对此的看法。
我的输入数据包含 1008 个特征,每个特征取值为 0/1,表示一个人在 10 分钟的时间间隔内是否在家。
我的目标是让 GAN 创建这种活动配置文件。然而,我面临的问题是,我的 GAN 目前创建的配置文件中,单个时间步长活动持续时间(一个人外出 10 分钟然后再次在家,或者反之亦然:在家 10 分钟然后再次外出)的比例高于真实数据。其他活动持续时间(20 分钟、30 分钟、40 分钟……)的比例非常接近真实数据!这真的很让我困惑……GAN 模型除了这些小错误过多之外,还创建了逼真的数据。
您对此有什么看法?什么可以解决这个问题?
此致,
Abdullah
您也许应该使用一个生成模型,允许您施加约束以确保生成的数据是合理的。
也许可以研究一下概率图模型。
如何减少生成图像中的噪声?
Dropout 和 Adam 可以用于 GAN 吗?
这里有一些想法
https://machinelearning.org.cn/how-to-code-generative-adversarial-network-hacks/
嗨,Jason,
非常感谢这篇精彩的文章。我有两个问题
问题 1:我训练了一个 GAN 并获得了下面 URL 图像中显示的对数损失。我该如何解释这个?更具体地说,它如何说明以下几点:
https://drive.google.com/file/d/1F7U8CJoSFEC81B8FyOXwu9LhikUD3-vi/view?usp=sharing
(i) 生成器收敛
(ii) 鉴别器性能
(iii) 训练应在哪次迭代停止?
(iv) 在哪次迭代产生的生成器模型应用于生成逼真的数据?
问题 2:训练 GAN 后,为什么我们不使用最后一次迭代产生的生成器模型来生成逼真的数据?难道 GAN 的收敛性随着训练迭代次数的增加而提高吗?
GAN 不会收敛
https://machinelearning.org.cn/faq/single-faq/why-is-my-gan-not-converging
不。您在整个运行过程中保存模型,测试每个模型,然后选择一个能够产生您喜欢的结果的模型。
嗨,Jason,
感谢您的回答。您能否也看一下我帖子中的第一个问题?
从图中来看,训练过程可能是稳定的。
感谢这篇精彩的文章!它非常有用。
两个有趣的问题对我来说仍然是暗物质。
1. 潜在空间大小如何影响模型收敛?
2. 模型容量(可训练参数总数)的一般建议是什么?以及如何避免对给定任务所需的容量进行高估/低估。
您能否分享您的直觉?
再次感谢您提供的精彩文章。
GAN 不会收敛
https://machinelearning.org.cn/faq/single-faq/why-is-my-gan-not-converging
我们没有关于模型大小与能力的良好理论。我们所能做的最好的就是进行受控实验。
你好教授!
一如既往的精彩文章。
它帮助我很多地弄清楚了我的模型是如何工作的。
我有一个问题!我注意到您使用了标准差为 0.02 的随机正态初始化,我想知道这是为什么。
我刚刚在我的梯度中遇到了 Nan,我怀疑错误的初始化器可能是导致它的原因。(它是 glorot uniform,这是默认初始化器)。
我启用了梯度裁剪,所以不确定梯度在哪里会过冲。
您对此有何建议?
谢谢!
诚挚地
我不是教授。
您可以在这里看到原因
https://machinelearning.org.cn/how-to-code-generative-adversarial-network-hacks/
你好 Jason,
非常感谢您非常直观和富有启发性的课程!
多亏了您,我实现了一个辅助分类器 GAN 来生成一些医学图像。
架构或多或少与此相同
https://drive.google.com/file/d/1vFcfb9JuBovlfAN4ajBdcTtmMbxOn35z/view?usp=sharing
见 [1]。
经过一些训练后,我的学习曲线总是如下所示
https://drive.google.com/file/d/1AbTV41MizaJJaxYEOJSkV2wgKI9G4W9S/view?usp=sharing
您的建议非常有启发性,在实现和修改一些架构后,曲线看起来是这样的
https://drive.google.com/file/d/1yoH9voIv6xyFKHogg_AnnGMjuEyBm3hu/view?usp=sharing
并不完美,但通过观察曲线和输出图像,这是迄今为止最好的训练。
但是,对于每个类别,生成器每次都会生成相同的图像变体或噪声图像。
您有什么建议吗?
再次感谢您的课程!
[1] Madani A. et al., Deep echocardiography: data-efficient supervised and semi-supervised deep learning towards automated diagnosis of cardiac desease, In: NPJ Digital Medicine vol 1. 2018.
干得好!
抱歉,我不打开附件。
也许可以尝试调整模型或训练参数?进行实验。
你好
您能分享您的代码吗?
你好,
我复制粘贴了此代码,但结果完全不同(即未收敛)。是否可以将代码设置为确定性的?
谢谢
GAN 不会收敛
https://machinelearning.org.cn/faq/single-faq/why-is-my-gan-not-converging
不,学习算法的随机性是其特性,而不是 bug。
感谢您的回复,但我不同意。尽管我理解 GAN 的随机性,但测试中的非确定性从来都不是一个特性,尤其是在它阻止一篇文章被复现时:应该提供一个种子以使其确定性和可复现。
感谢分享您的观点。
嗨,Jason,
感谢您提供如此精彩的文章。
我有一个问题,是关于堆叠真实和虚假图像来训练鉴别器。
我尝试了代码,得到了与您相同的结果。让我感到困惑的是 G 的损失和 D 的准确率。正如我们所观察到的,D 的准确率接近 100%,这意味着 D 几乎可以正确识别每个图像(部分原因是生成虚假图像的质量很差,它们似乎很容易被识别)。但是,为什么 G 的损失这么低呢?凭直觉,生成的虚假图像很容易被识别为假的,G 的损失应该很高。您能告诉我哪里错了,谢谢。
不客气!
准确率可能是训练期间不应监视的糟糕指标。
而且,损失并不能说明 GAN 的技能,例如,GAN 不会收敛,它们定义上就是不稳定的。
https://machinelearning.org.cn/faq/single-faq/why-is-my-gan-not-converging
嗨,Jason,
很棒的教程!!我遇到了 GAN 的一个问题,损失在范围内并趋于稳定,但我的鉴别器准确率似乎无法超过真实和虚假图像的 50%,尽管我使用了预训练模型。可能是什么错误?
谢谢。
忽略准确率,它不是一个可靠的指标。关注损失。
而且所有的输出图像看起来都只是纯灰色的图像。
也许可以尝试更改模型的架构或学习算法的超参数。
https://machinelearning.org.cn/how-to-code-generative-adversarial-network-hacks/
感谢这篇文章
我的生成器损失显示出很大的波动,从 -500 到 +500,但鉴别器损失几乎恒定,在 0.3 到 0.6 之间波动。请帮助我,我真的卡住了。
也许可以关注生成的图像,看看它们是否好。
嗨,Jason,
我是一名人工智能硕士候选人。
我正在使用 cGan 模型来生成可靠的 COVID-19 CXR,并且我发现您的帖子很有用。
感谢您提供的有益解释。
我非常欣赏您的努力和您的热情。
致以最诚挚的问候,
Stefanos
不客气!
非常实用且有用的指南!
期待 StyleGAN 实现。
只是一个小提示:也许您在最后一节的这句话中是指“增加”
生成器的损失预计在训练期间会下降到零或持续下降。
谢谢!
谢谢!
为什么我们期望损失增加?
如果我理解正确的话,在下面的段落中,您展示了 GAN 训练过程中收敛失败的特性。在这些特性中,我们发现(如您所提到的):生成器的损失预计会下降到零或在训练期间持续“增加”。
如果我错了,请纠正我。
谢谢!
—————————————————————————————
我们可以按如下方式审查收敛失败的特性:
—) 鉴别器的损失预计会迅速下降到接近零的值,并在训练期间保持在该值。
—) 生成器的损失预计在训练期间会下降到零或持续下降。
—) 生成器预计会产生极低质量的图像,很容易被鉴别器识别为伪造。
作为经验法则,这些对于 DCGAN 来说是一个很好的起点。
非常好,谢谢!
不客气!
嗨 Jason,感谢这篇精彩的文章。
以下是我遇到的一些问题和疑问
1:
我准确地复制了稳定 GAN 的文章代码。
但我的图表似乎完全不匹配,我从您的稳定 GAN 代码中得到的图表似乎与收敛失败代码的图表相匹配。
生成的图像几乎是垃圾,正如预期的那样。
2:
我发现这篇文章中用于“epoch”的术语非常令人困惑。
一个 epoch 是模型被训练整个数据集一次,对吧?
epoch 的这个定义符合代码中的定义。
然而,当您在文章中提到 epoch 时,您指的是训练批次的每一步。
您能否对此进行澄清?
谢谢。
您可能需要尝试训练几次GAN,才能获得有用的模型/可靠的训练过程。
同意!!! Epoch对于GAN来说已经没有意义了。它真的是单个批次的迭代。
这篇帖子中使用的GAN基本上是DCGAN吗?因为它使用了卷积层?
当然,但我们的概念普遍适用于大多数GAN。
你好
感谢您的文章
我有一个问题。
我正在处理3D图像,并使用了Adam优化器。我为鉴别器设置的学习率为 1e-04,为生成器设置的学习率为 1.1e-05。
我的鉴别器损失在0.4-0.6之间波动,但生成器损失却在上升。
您能帮帮我吗?
可以试试直接使用SGD,并探索不同的学习率。
Jason,感谢您精彩的教程!如果您发现鉴别器真实图像损失在一个不错的范围(约0.5),但鉴别器假图像损失和生成器损失都趋于零,您会怎么做?这让我很不确定生成器或鉴别器是太弱/太强了,因为鉴别器假图像损失为零表明鉴别器太强,能够清晰地识别假图像,但生成器损失为零又表明生成器太强……您对此有什么建议吗?非常感谢!
通过移除BatchNormalization层解决了这个问题!
太棒了!
不客气。
GANs 没有好的损失值,而是需要关注两种模型的动态。损失值为零可能是一个坏迹象——意味着一个模型占主导地位。
Jason,您说:“一个稳定的GAN,鉴别器损失在0.5左右,通常在0.5到0.7或0.8之间。生成器损失通常更高,可能在1.0、1.5、2.0甚至更高。”
您能给我一些更详细地解释为什么这些值是理想的吗?我正在尝试理解二元交叉熵的数学原理,以及为什么这些是最优值,是否有任何论文/文章对此进行了更深入的探讨?谢谢。
不,这源于经验。我们还没有好的GAN理论。
嗨,Jason,
非常感谢您写了一篇很好的文章!我有一个额外的问题。我正在自己训练一个Wasserstein GAN。正如您可能知道的,这些GAN在最后没有softmax激活,相应地,“鉴别器”实际上不是鉴别器,而是“批评家”。这意味着我没有准确率,我的损失也很不一样。
您知道对于Wasserstein GAN,是否有类似的方法可以从损失函数(或任何其他我可能计算的指标)来识别收敛失败或模式崩溃吗?
据我所知,没有。取而代之的是,每隔n个epoch观察生成的图像,以了解模型运行得如何。
Jason你好,这是一篇非常棒的教程!我有一个问题。我发现我的GAN出现了模式崩溃。我该如何修复?如何修复一个正在经历模式崩溃的GAN?
鉴别器真实图像损失在0.6左右,鉴别器假图像损失在0.7左右,生成器损失大部分时间都在0.55左右(这些值有时会变化,但大多数时间都保持这些值)。如何修复正在经历模式崩溃的GAN?
请记住,要关注生成的图像,而不是损失值。
谢谢!
或许可以试试这些方法
https://machinelearning.org.cn/how-to-code-generative-adversarial-network-hacks/
我改编了您模型中的很多部分,并根据您论文中的实现,在运动模糊和失焦的模糊数据上进行了训练。在100个epoch后,我得到的图片几乎是准确的,但像素化非常严重。我没有创建检查点,只有最后一个(第100个)模型。您能否给我一种方法,让我可以从第100个模型重新开始多次训练……以及关于如何在模型中增加图片清晰度的其他建议?
是的,这些技巧会给您一些尝试的方向。
https://machinelearning.org.cn/how-to-code-generative-adversarial-network-hacks/
Jason你好,这篇文章写得太棒了!
1. 我不明白为什么在第一个不收敛的例子中,两个损失都趋于0。
这难道不是一个零和博弈吗?当鉴别器趋于0时,GAN的损失不应该上升吗?
2. 当出现第二个问题“不收敛”时,我应该怎么做?
谢谢!
损失不可能都趋于零,其中一个模型(例如鉴别器)会有一个零损失,而另一个会接近零但不为零。
GAN是不会收敛的。
这些技巧将有助于提高GAN的性能。
https://machinelearning.org.cn/how-to-code-generative-adversarial-network-hacks/
嗨,Jason,
好文!
我在PyTorch中创建了一个与您非常相似的GAN版本。
我用它来预测温度图,而不是真实的RGB或二值图像。
不知何故,我的鉴别器在开始时就卡在第一个迭代的相同损失0.693,既不上升也不下降,您对此有什么看法?
另外,我能否将生成器的最后一层从Tanh改为ReLU,因为我的图被归一化在0-1之间?
谢谢。
干得好。
也许这里的某些建议会有所帮助
https://machinelearning.org.cn/how-to-code-generative-adversarial-network-hacks/
嗨,Jason,
好文章!
我为文本行图像去噪构建了一个GAN。然而,在训练过程中,我注意到每4个epoch在验证数据上评估的PSNR并不稳定,如下所示:
epoch psnr
0 11.23549198
1 11.06054743
2 13.47806442
3 15.43679847
4 16.32856713
5 16.41565544
8 5.565504805
12 17.37565203
16 17.53865563
尤其是在第8个epoch,这种行为正常吗?
谢谢你。
我不认为训练GAN有什么“正常”可言。
或许应该关注模型的性能而不是损失,除非出现模式失败。
先生,鉴别器模型和生成器模型的最后一层分别是sigmoid和tanh激活。sigmoid函数的范围是[0到1],tanh的范围是[-1到0]。但是,d损失和g损失都超出了这些范围,无论是在稳定的GAN还是不稳定的GAN中。
请尽快回复。
审查GAN的损失值无助于判断它是否拟合良好,例如,GAN不会收敛。
https://machinelearning.org.cn/faq/single-faq/why-is-my-gan-not-converging
你好,我试用了这段代码,在训练了几个epoch后出现了这个错误:
TypeError: unsupported operand type(s) for *: ‘Sequential’ and ‘int’ at line 3 x_input =rand(latent *)
def generate_latent_points(latent_dim, n_samples)
# generate points in the latent space
x_input = randn(latent_dim * n_samples)
# reshape into a batch of inputs for the network
x_input = x_input.reshape(n_samples, latent_dim)
print(x_input)
return x_input
抱歉,不小心将Sequential数据通过了summurization函数。
不客气。
听到这个消息很抱歉,这可能会有帮助
https://machinelearning.org.cn/faq/single-faq/why-does-the-code-in-the-tutorial-not-work-for-me
你好,
我在半监督GAN中通过移除鉴别器中的Batch Norm层来修复了GAN的失败模式。但现在我注意到生成器根本无法欺骗鉴别器,所以鉴别器的准确率是100%。
您可以忽略准确率。
关注生成的图像。
这篇绝妙的文章,感谢您的发布。
我有一个关于数据集大小与是否会影响GAN稳定性之间关系的问题。
也就是说,如果数据集很小,理论上是否需要更长的时间才能达到平衡?是否存在数据集最小尺寸的阈值,使得GAN永远无法达到平衡?
谢谢!
我确定有,我认为在这个阶段很难描述这种关系。
一如既往的优秀,感谢您的发布!
我的鉴别器损失接近于零(例如0.032),同时生成器损失在3.988左右。这大约在第20个epoch发生,并持续到第40个epoch(这是我尝试训练模型的范围)。这是否意味着我应该放弃训练?查看结果图像有点不确定,因为我正在尝试处理声谱图,它们的出现并没有给我关于GAN运行情况的线索。它可能在许多epoch后得到改善,也可能不会。我也不想徒劳地等待。
另外,我如何使用这个模型恢复训练?如何加载权重,又在哪个模型上加载它们?
图像质量是判断的主要依据,而且它也可能稍后变好。
您可以随时保存/加载图像,例如:
https://machinelearning.org.cn/save-load-keras-deep-learning-models/
你好,
您能解释一下为什么如果GAN不收敛,鉴别器和生成器损失都会接近零?如果鉴别器擅长识别哪些图像是真实的,哪些是伪造的,那么为什么它会被生成器欺骗?
谢谢
是的,请看这个
https://machinelearning.org.cn/faq/single-faq/why-is-my-gan-not-converging
我发现了您训练的假图像,比如数字8,在数字8周围有一些伪影。那么,在训练GAN时,如何减少生成图像中的伪影呢?
您或许可以尝试这里的GAN技巧:https://machinelearning.org.cn/how-to-code-generative-adversarial-network-hacks/
Jason你好,首先感谢您这篇精彩的文章!
您是否遇到过在训练了20个epoch后突然模型失败的情况?一开始一切都很好,然后突然在某个epoch,模型完全失败并生成垃圾图片。
我把生成的图片和损失曲线图放在这里
https://docs.google.com/document/d/1EGNLhIbN2PS91vx93rDG54IPBGgPoova/edit?usp=sharing&ouid=105449882848905790783&rtpof=true&sd=true
这是可能的。因此,您需要监控损失并停止训练。
生成器权重在训练过程中变为NaN:
我正在使用皮肤癌数据集(https://challenge.isic-archive.com/data – 2016,仅黑色素瘤)进行GAN训练。在多个epoch后,生成器权重变成NaN(我认为是因为float32过大)。
我尝试了DCGAN(Adam和SGD -> 优化器)、bigGAN、我自己制作的自定义模型。
我尝试添加/删除谱归一化层、批量归一化层和正则化器,但都没有帮助。
我也检查了数据中的空值(没有发现)。
在我最后的几次实验中,我做了以下操作:
# 批次大小 -> 128,dis-lr : 1E-4,gen-lr : 4E-4,无空值,直到约1650个epoch
# 批次大小 -> 256,dis-lr : 1E-4,gen-lr : 4E-4,第162个epoch出现空值
# 批次大小 -> 512,dis-lr : 1E-4,gen-lr : 16E-4,第1439个epoch出现空值
使用优化器 -> SGD;动量 -> 0.9;目标图像大小 64 x 64 x 3;
这背后的真正原因是什么?
我阅读了各种github / stack overflow页面,但它们都没有帮助我。
页面链接 ->
1. https://stackoverflow.com/questions/33962226/common-causes-of-nans-during-training
2. https://stackoverflow.com/questions/52211665/why-do-i-get-nan-loss-value-in-training-discriminator-and-generator-of-gan
3. https://github.com/eriklindernoren/Keras-GAN/issues/87
4. https://github.com/tensorflow/tensorflow/issues/38416
如果您的权重是NaN,那很可能是由于梯度爆炸。您可能需要调整您的优化器。请参阅此示例中的SGD:https://stackoverflow.com/questions/52000103/weights-of-keras-model-are-nan
嗨,Jason,
我运行模型3000个epoch,但鉴别器损失在第5个epoch就降到了0,准确率也达到了100%。
10个epoch后,生成器损失接近1。
使用Pix2Pix GAN。
您对此有什么看法?
Aditi你好…你可能正在处理一个回归问题,并实现了零预测误差。
或者,你可能正在处理分类问题并实现 100% 的准确率。
这很不寻常,原因有很多,包括:
你不小心在训练集上评估了模型性能。
你的保留数据集(训练集或验证集)太小或不具代表性。
你的代码中引入了一个错误,它正在做一些与你预期不同的事情。
你的预测问题很容易或微不足道,可能不需要机器学习。
最常见的原因是你的保留数据集太小或不代表更广泛的问题。
可以通过以下方法解决:
使用 k 折交叉验证来估计模型性能,而不是训练/测试拆分。
收集更多数据。
使用不同的数据拆分进行训练和测试,例如 50/50。
你好!
仍在学习GAN
当我的鉴别器准确率在0和1之间来回波动时,这意味着什么?
TIA!
Nandini你好…您可能会对以下内容感兴趣:
https://neptune.ai/blog/gan-loss-functions
在良好模型的伪代码中,您的latent_size等于50。这会导致模型崩溃。您提到将latent_size从“100改为1”会导致模型崩溃,所以我假设latent_size实际上应该是100,而不是50!
Alexandras,感谢您的精彩反馈!我们非常感谢!
你好
我需要一篇陈述FID指标和IS指标的论文或书籍。
请务必需要它们,以便了解改进情况。
Israa你好…请重新表述和/或澄清您的问题,以便我们能更好地帮助您。
这篇文章很棒,谢谢。
不客气!感谢您的反馈和支持!