预测区间为回归问题提供预测的不确定性度量。
例如,95%的预测区间表示有95%的时间,真实值将落在范围的下限和上限之间。这不同于可能代表不确定性区间中心的简单点预测。
目前没有计算深度学习神经网络在回归预测建模问题上预测区间上的标准技术。尽管如此,可以通过模型集成来估计一个快速而简便的预测区间,集成模型进而提供点预测的分布,从中可以计算出区间。
在本教程中,您将学习如何为深度学习神经网络计算预测区间。
完成本教程后,您将了解:
- 预测区间为回归预测建模问题提供不确定性度量。
- 如何为标准回归问题开发和评估简单的多层感知器神经网络。
- 如何使用神经网络模型集成来计算和报告预测区间。
让我们开始吧。

深度学习神经网络的预测区间
照片由 eugene_o 提供,保留部分权利。
教程概述
本教程分为三个部分;它们是:
- 预测区间
- 用于回归的神经网络
- 神经网络预测区间
预测区间
通常,回归问题的预测模型(即预测数值)会进行点预测。
这意味着它们预测一个单一值,但没有提供任何关于预测不确定性的指示。
根据定义,预测是估计或近似值,并包含一些不确定性。不确定性来自模型本身的错误和输入数据的噪声。模型是输入变量与输出变量之间关系的近似。
预测区间是对预测不确定性的量化。
它为结果变量的估计提供概率性的上限和下限。
单个未来观测值的预测区间是一个区间,在指定的置信度下,该区间将包含来自分布的随机选择的未来观测值。
— 第 27 页,Statistical Intervals: A Guide for Practitioners and Researchers, 2017。
预测区间最常用于使用回归模型进行预测或预报时,其中正在预测一个数量。
预测区间围绕模型做出的预测,并希望覆盖真实结果的范围。
有关预测区间的更多信息,请参阅教程
现在我们对预测区间有了了解,可以考虑如何为神经网络计算区间。让我们从定义一个回归问题和一个用于解决该问题的神经网络模型开始。
用于回归的神经网络
在本节中,我们将定义一个回归预测建模问题和一个用于解决该问题的神经网络模型。
首先,让我们引入一个标准的回归数据集。我们将使用住房数据集。
住房数据集是一个标准的机器学习数据集,包含 506 行数据,其中有 13 个数值输入变量和一个数值目标变量。
使用具有三次重复的10折分层交叉验证的测试框架,朴素模型可以达到大约6.6的平均绝对误差(MAE)。一个表现最佳的模型可以在同一测试框架上达到约1.9的MAE。这提供了该数据集上的预期性能范围。
该数据集涉及根据美国波士顿郊区的房屋细节来预测房价。
无需下载数据集;我们将在工作示例中自动下载它。
下面的示例下载并以 Pandas DataFrame 的形式加载数据集,并总结了数据集的形状和前五行数据。
|
1 2 3 4 5 6 7 8 9 10 |
# 加载和汇总住房数据集 from pandas import read_csv from matplotlib import pyplot # 加载数据集 url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/housing.csv' dataframe = read_csv(url, header=None) # 总结形状 print(dataframe.shape) # 总结前几行 print(dataframe.head()) |
运行示例,确认了 506 行数据和 13 个输入变量以及一个数值目标变量(共 14 个)。我们还可以看到所有输入变量都是数值型的。
|
1 2 3 4 5 6 7 8 9 |
(506, 14) 0 1 2 3 4 5 ... 8 9 10 11 12 13 0 0.00632 18.0 2.31 0 0.538 6.575 ... 1 296.0 15.3 396.90 4.98 24.0 1 0.02731 0.0 7.07 0 0.469 6.421 ... 2 242.0 17.8 396.90 9.14 21.6 2 0.02729 0.0 7.07 0 0.469 7.185 ... 2 242.0 17.8 392.83 4.03 34.7 3 0.03237 0.0 2.18 0 0.458 6.998 ... 3 222.0 18.7 394.63 2.94 33.4 4 0.06905 0.0 2.18 0 0.458 7.147 ... 3 222.0 18.7 396.90 5.33 36.2 [5 行 x 14 列] |
接下来,我们可以准备用于建模的数据集。
首先,数据集可以分为输入和输出列,然后行可以分为训练集和测试集。
在这种情况下,我们将使用大约67%的行来训练模型,其余33%来评估模型的性能。
|
1 2 3 4 5 |
... # 将数据集分为输入和输出值 X, y = values[:,:-1], values[:,-1] # 拆分为训练集和测试集 X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.67) |
您可以在本教程中了解更多关于训练集和测试集划分的信息
然后,我们将所有输入列(变量)缩放到0-1的范围,称为数据归一化,这在使用神经网络模型时是一个好习惯。
|
1 2 3 4 5 6 |
... # 缩放输入数据 scaler = MinMaxScaler() scaler.fit(X_train) X_train = scaler.transform(X_train) X_test = scaler.transform(X_test) |
您可以在本教程中了解更多关于使用MinMaxScaler归一化输入数据的信息
准备用于建模的完整数据示例列在下面。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# 加载并准备用于建模的数据集 from pandas import read_csv from sklearn.model_selection import train_test_split from sklearn.preprocessing import MinMaxScaler # 加载数据集 url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/housing.csv' dataframe = read_csv(url, header=None) values = dataframe.values # 将数据集分为输入和输出值 X, y = values[:,:-1], values[:,-1] # 拆分为训练集和测试集 X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.67) # 缩放输入数据 scaler = MinMaxScaler() scaler.fit(X_train) X_train = scaler.transform(X_train) X_test = scaler.transform(X_test) # 总结 print(X_train.shape, X_test.shape, y_train.shape, y_test.shape) |
运行该示例将像以前一样加载数据集,然后将列拆分为输入和输出元素,将行拆分为训练集和测试集,最后将所有输入变量缩放到[0,1]范围
训练集和测试集的形状被打印出来,显示我们有339行用于训练模型,167行用于评估。
|
1 |
(339, 13) (167, 13) (339,) (167,) |
接下来,我们可以在数据集上定义、训练和评估多层感知器(MLP)模型。
我们将定义一个简单的模型,包含两个隐藏层和一个预测数值的输出层。我们将使用ReLU激活函数和“he”权重初始化,这些都是良好的实践。
每个隐藏层中的节点数量是在经过一些试验和错误后确定的。
|
1 2 3 4 5 6 7 |
... # 定义神经网络模型 features = X_train.shape[1] model = Sequential() model.add(Dense(20, kernel_initializer='he_normal', activation='relu', input_dim=features)) model.add(Dense(5, kernel_initializer='he_normal', activation='relu')) model.add(Dense(1)) |
我们将使用高效的Adam版本的随机梯度下降,并使用接近默认值的学习率和动量值,并使用均方误差(MSE)损失函数来拟合模型,这是回归预测建模问题的标准。
|
1 2 3 4 |
... # 编译模型并指定损失和优化器 opt = Adam(learning_rate=0.01, beta_1=0.85, beta_2=0.999) model.compile(optimizer=opt, loss='mse') |
您可以在本教程中了解更多关于Adam优化算法的信息
模型将以16个样本的批次大小拟合300个时期。此配置是在经过一些试验和错误后确定的。
|
1 2 3 |
... # 在训练数据集上拟合模型 model.fit(X_train, y_train, verbose=2, epochs=300, batch_size=16) |
您可以在本教程中了解更多关于批次和时期(epochs)的信息
最后,模型可用于在测试数据集上进行预测,并且我们可以通过将其与测试集中的预期值进行比较来评估预测,并计算平均绝对误差(MAE),这是一个有用的模型性能度量。
|
1 2 3 4 5 6 |
... # 对测试集进行预测 yhat = model.predict(X_test, verbose=0) # 计算预测中的平均误差 mae = mean_absolute_error(y_test, yhat) print('MAE: %.3f' % mae) |
将这些结合起来,完整的示例列在下面。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
# 在住房回归数据集上训练和评估多层感知器神经网络 from pandas import read_csv from sklearn.model_selection import train_test_split from sklearn.metrics import mean_absolute_error 从 sklearn.预处理 导入 MinMaxScaler from tensorflow.keras.models import Sequential from tensorflow.keras.layers import Dense from tensorflow.keras.optimizers import Adam # 加载数据集 url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/housing.csv' dataframe = read_csv(url, header=None) values = dataframe.values # 将数据集分为输入和输出值 X, y = values[:, :-1], values[:,-1] # 拆分为训练集和测试集 X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.67, random_state=1) # 缩放输入数据 scaler = MinMaxScaler() scaler.fit(X_train) X_train = scaler.transform(X_train) X_test = scaler.transform(X_test) # 定义神经网络模型 features = X_train.shape[1] model = Sequential() model.add(Dense(20, kernel_initializer='he_normal', activation='relu', input_dim=features)) model.add(Dense(5, kernel_initializer='he_normal', activation='relu')) model.add(Dense(1)) # 编译模型并指定损失和优化器 opt = Adam(learning_rate=0.01, beta_1=0.85, beta_2=0.999) model.compile(optimizer=opt, loss='mse') # 在训练数据集上拟合模型 model.fit(X_train, y_train, verbose=2, epochs=300, batch_size=16) # 对测试集进行预测 yhat = model.predict(X_test, verbose=0) # 计算预测中的平均误差 mae = mean_absolute_error(y_test, yhat) print('MAE: %.3f' % mae) |
运行该示例将加载和准备数据集,定义并拟合MLP模型在训练数据集上,并在测试集上评估其性能。
注意:由于算法或评估程序的随机性,或者数值精度的差异,您的结果可能会有所不同。考虑运行该示例几次并比较平均结果。
在这种情况下,我们可以看到模型实现了大约2.3的平均绝对误差,这比朴素模型要好,并且接近最优模型。
毫无疑问,通过进一步调整模型,我们可以实现接近最优的性能,但这对于我们对预测区间的调查来说已经足够了。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
... 第 296/300 轮 22/22 - 0s - loss: 7.1741 第 297/300 轮 22/22 - 0s - loss: 6.8044 第 298/300 轮 22/22 - 0s - loss: 6.8623 第 299/300 轮 22/22 - 0s - loss: 7.7010 第 300/300 轮 22/22 - 0s - loss: 6.5374 MAE: 2.300 |
接下来,我们来看看如何使用MLP模型在住房数据集上计算预测区间。
神经网络预测区间
在本节中,我们将使用上一节中开发的回归问题和模型来开发预测区间。
与线性回归等线性方法相比,为神经网络等非线性回归算法计算预测区间具有挑战性,而线性回归的预测区间计算非常简单。没有标准技术。
有许多方法可以为神经网络模型计算有效的预测区间。我推荐“进一步阅读”部分中列出的一些论文以了解更多信息。
在本教程中,我们将使用一种非常简单的方法,该方法有很多扩展的空间。我称之为“快速而简便”,因为它计算速度快且容易,但有局限性。
它涉及拟合多个最终模型(例如10到30个)。然后使用集成成员的点预测分布来计算点预测和预测区间。
例如,点预测可以取自集成成员的点预测的平均值,而95%的预测区间可以取为均值加减1.96个标准差。
这是一个简单的高斯预测区间,尽管也可以使用替代方法,例如点预测的最小值和最大值。或者,可以使用bootstrap方法对每个集成成员进行不同的bootstrap样本训练,然后将点预测的第2.5个和第97.5个百分位数用作预测区间。
有关bootstrap方法的更多信息,请参阅教程
这些扩展留作练习;我们将坚持简单的高斯预测区间。
假设上一节中定义的训练数据集是整个数据集,并且我们在整个数据集上训练一个或多个最终模型。然后,我们可以使用预测区间对测试集进行预测,并评估该区间在未来可能多么有效。
我们可以通过将上一节中开发的元素分成函数来简化代码。
首先,让我们定义一个用于加载和准备由URL定义的回归数据集的函数。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# 加载并准备数据集 def load_dataset(url): dataframe = read_csv(url, header=None) values = dataframe.values # 将数据集分为输入和输出值 X, y = values[:, :-1], values[:,-1] # 将数据集分为训练集和测试集 X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.67, random_state=1) # 缩放输入数据 scaler = MinMaxScaler() scaler.fit(X_train) X_train = scaler.transform(X_train) X_test = scaler.transform(X_test) return X_train, X_test, y_train, y_test |
接下来,我们可以定义一个函数,该函数将定义和训练一个MLP模型,该模型以训练数据集为输入,然后返回已拟合的模型,准备好进行预测。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# 定义并拟合模型 def fit_model(X_train, y_train): # 定义神经网络模型 features = X_train.shape[1] model = Sequential() model.add(Dense(20, kernel_initializer='he_normal', activation='relu', input_dim=features)) model.add(Dense(5, kernel_initializer='he_normal', activation='relu')) model.add(Dense(1)) # 编译模型并指定损失和优化器 opt = Adam(learning_rate=0.01, beta_1=0.85, beta_2=0.999) model.compile(optimizer=opt, loss='mse') # 在训练数据集上拟合模型 model.fit(X_train, y_train, verbose=0, epochs=300, batch_size=16) return model |
我们需要多个模型来进行点预测,这些点预测将构成一个点预测分布,我们可以从中估计区间。
因此,我们需要在训练数据集上拟合多个模型。每个模型都必须不同,以便它做出不同的预测。这可以通过MLP模型的随机性来实现,给定随机的初始权重,以及使用随机梯度下降优化算法。
模型越多,点预测对模型能力的估计就越好。我建议至少10个模型,并且可能超过30个模型收益不大。
下面的函数拟合了模型集成,并将它们存储在一个返回的列表中。
出于兴趣,每个已拟合的模型也将在测试集上进行评估,该评估将在每个模型拟合后报告。我们预计每个模型在保留的测试集上的估计性能将略有不同,并且报告的分数将帮助我们确认这一期望。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
# 拟合模型集成 def fit_ensemble(n_members, X_train, X_test, y_train, y_test): ensemble = list() for i in range(n_members): # 在训练集上定义并拟合模型 model = fit_model(X_train, y_train) # 在测试集上评估模型 yhat = model.predict(X_test, verbose=0) mae = mean_absolute_error(y_test, yhat) print('>%d, MAE: %.3f' % (i+1, mae)) # 存储模型 ensemble.append(model) return ensemble |
最后,我们可以使用训练好的模型集成来进行点预测,这些点预测可以汇总为预测区间。
下面的函数实现了这一点。首先,每个模型对输入数据进行点预测,然后计算95%的预测区间,并返回区间的下限、均值和上限。
该函数设计为接受单个行作为输入,但也可以轻松地将其改编为处理多行。
|
1 2 3 4 5 6 7 8 9 |
# 使用集成进行预测并计算预测区间 def predict_with_pi(ensemble, X): # 进行预测 yhat = [model.predict(X, verbose=0) for model in ensemble] yhat = asarray(yhat) # 计算95%高斯预测区间 interval = 1.96 * yhat.std() lower, upper = yhat.mean() - interval, yhat.mean() + interval return lower, yhat.mean(), upper |
最后,我们可以调用这些函数。
首先,加载并准备数据集,然后定义并拟合集成模型。
|
1 2 3 4 5 6 7 |
... # 加载数据集 url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/housing.csv' X_train, X_test, y_train, y_test = load_dataset(url) # 拟合集成模型 n_members = 30 ensemble = fit_ensemble(n_members, X_train, X_test, y_train, y_test) |
然后,我们可以使用测试集中的单行数据进行预测,并包含预测区间,然后报告结果。
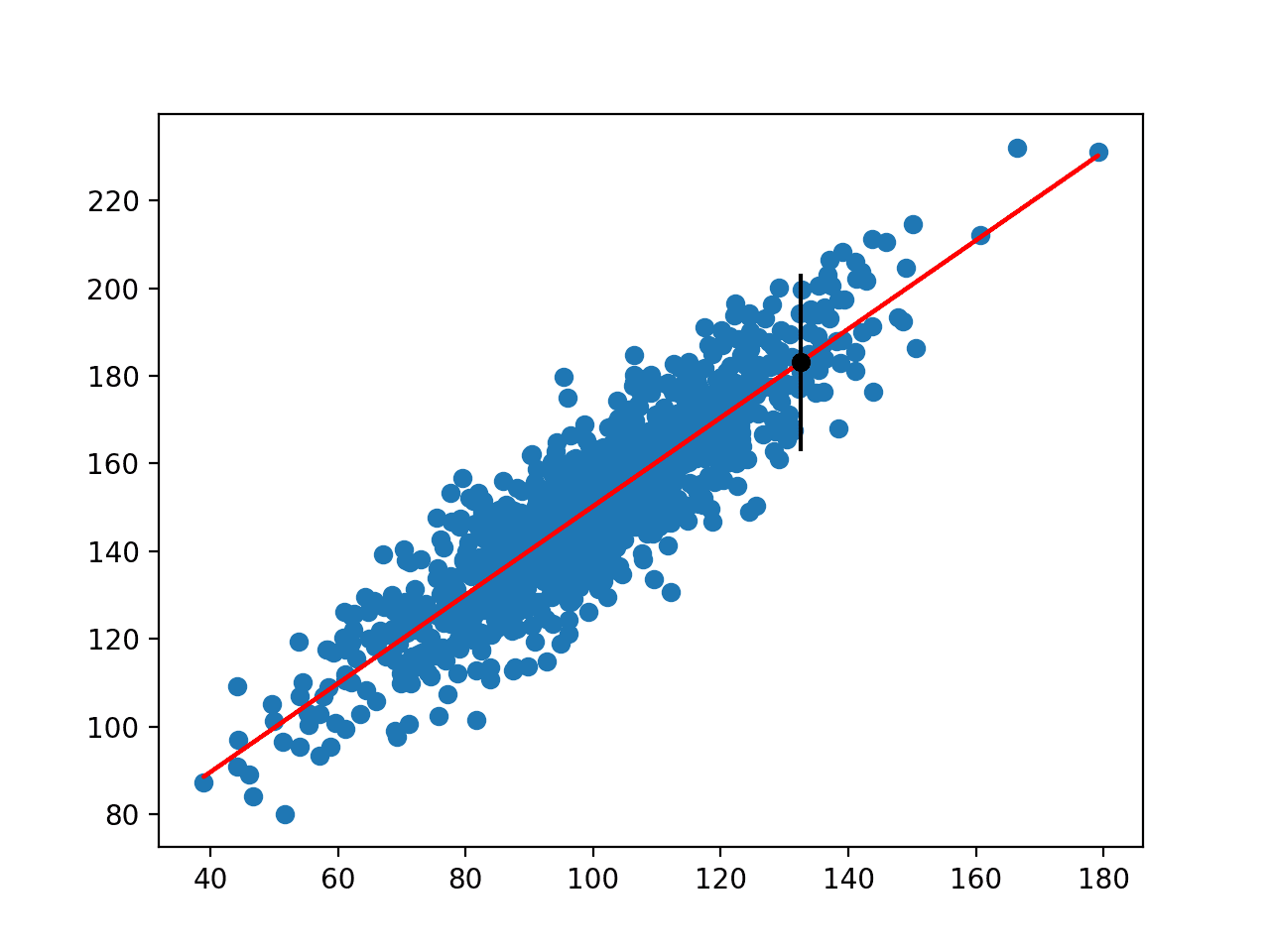
我们还报告了预期值,该值应包含在预测区间内(可能约 95% 的时间;这并不完全准确,但是一个粗略的近似)。
|
1 2 3 4 5 6 7 |
... # 进行带预测区间的预测 newX = asarray([X_test[0, :]]) lower, mean, upper = predict_with_pi(ensemble, newX) print('点预测: %.3f' % mean) print('95%% 预测区间: [%.3f, %.3f]' % (lower, upper)) print('真实值: %.3f' % y_test[0]) |
将这些内容汇总起来,下面列出了使用多层感知器神经网络进行带预测区间的预测的完整示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 |
# 在房价回归数据集上进行 MLP 的预测区间 from numpy import asarray from pandas import read_csv from sklearn.model_selection import train_test_split from sklearn.metrics import mean_absolute_error 从 sklearn.预处理 导入 MinMaxScaler from tensorflow.keras.models import Sequential from tensorflow.keras.layers import Dense from tensorflow.keras.optimizers import Adam # 加载并准备数据集 def load_dataset(url): dataframe = read_csv(url, header=None) values = dataframe.values # 将数据集分为输入和输出值 X, y = values[:, :-1], values[:,-1] # 将数据集分为训练集和测试集 X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.67, random_state=1) # 缩放输入数据 scaler = MinMaxScaler() scaler.fit(X_train) X_train = scaler.transform(X_train) X_test = scaler.transform(X_test) return X_train, X_test, y_train, y_test # 定义并拟合模型 def fit_model(X_train, y_train): # 定义神经网络模型 features = X_train.shape[1] model = Sequential() model.add(Dense(20, kernel_initializer='he_normal', activation='relu', input_dim=features)) model.add(Dense(5, kernel_initializer='he_normal', activation='relu')) model.add(Dense(1)) # 编译模型并指定损失和优化器 opt = Adam(learning_rate=0.01, beta_1=0.85, beta_2=0.999) model.compile(optimizer=opt, loss='mse') # 在训练数据集上拟合模型 model.fit(X_train, y_train, verbose=0, epochs=300, batch_size=16) return model # 拟合模型集成 def fit_ensemble(n_members, X_train, X_test, y_train, y_test): ensemble = list() for i in range(n_members): # 在训练集上定义并拟合模型 model = fit_model(X_train, y_train) # 在测试集上评估模型 yhat = model.predict(X_test, verbose=0) mae = mean_absolute_error(y_test, yhat) print('>%d, MAE: %.3f' % (i+1, mae)) # 存储模型 ensemble.append(model) return ensemble # 使用集成进行预测并计算预测区间 def predict_with_pi(ensemble, X): # 进行预测 yhat = [model.predict(X, verbose=0) for model in ensemble] yhat = asarray(yhat) # 计算95%高斯预测区间 interval = 1.96 * yhat.std() lower, upper = yhat.mean() - interval, yhat.mean() + interval return lower, yhat.mean(), upper # 加载数据集 url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/housing.csv' X_train, X_test, y_train, y_test = load_dataset(url) # 拟合集成模型 n_members = 30 ensemble = fit_ensemble(n_members, X_train, X_test, y_train, y_test) # 进行带预测区间的预测 newX = asarray([X_test[0, :]]) lower, mean, upper = predict_with_pi(ensemble, newX) print('点预测: %.3f' % mean) print('95%% 预测区间: [%.3f, %.3f]' % (lower, upper)) print('真实值: %.3f' % y_test[0]) |
运行示例将依次拟合每个集成成员,并报告其在保留测试集上的估计性能;最后,将进行一次带预测区间的预测并报告。
注意:由于算法或评估程序的随机性,或者数值精度的差异,您的结果可能会有所不同。考虑运行该示例几次并比较平均结果。
在这种情况下,我们可以看到每个模型的性能略有不同,这证实了我们对模型确实不同的预期。
最后,我们可以看到集成模型进行了约 30.5 的点预测,其 95% 预测区间为 [26.287, 34.822]。我们还可以看到真实值为 28.2,并且该区间确实包含了这个值,这很好。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
>1, MAE: 2.259 >2, MAE: 2.144 >3, MAE: 2.732 >4, MAE: 2.628 >5, MAE: 2.483 >6, MAE: 2.551 >7, MAE: 2.505 >8, MAE: 2.299 >9, MAE: 2.706 >10, MAE: 2.145 >11, MAE: 2.765 >12, MAE: 3.244 >13, MAE: 2.385 >14, MAE: 2.592 >15, MAE: 2.418 >16, MAE: 2.493 >17, MAE: 2.367 >18, MAE: 2.569 >19, MAE: 2.664 >20, MAE: 2.233 >21, MAE: 2.228 >22, MAE: 2.646 >23, MAE: 2.641 >24, MAE: 2.492 >25, MAE: 2.558 >26, MAE: 2.416 >27, MAE: 2.328 >28, MAE: 2.383 >29, MAE: 2.215 >30, MAE: 2.408 点预测: 30.555 95% 预测区间: [26.287, 34.822] 真实值: 28.200 |
正如我们上面讨论的,这是一种为神经网络进行带预测区间预测的快速而粗略的技术。
有一些简单的扩展,例如使用应用于点预测的 bootstrap 方法,这可能更可靠,我建议你探索下面列出的一些论文中描述的更高级的技术。
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
教程
- 机器学习的预测区间
- 如何在 Python 中使用 StandardScaler 和 MinMaxScaler 转换
- 标准机器学习数据集的最佳结果
- 神经网络中批次(Batch)和周期(Epoch)的区别
- 从头开始编写Adam梯度下降优化代码
论文
- 深度学习的高质量预测区间:一种无分布的集成方法, 2018.
- 实用的置信区间和预测区间, 1994.
文章
总结
在本教程中,你学习了如何为深度学习神经网络计算预测区间。
具体来说,你学到了:
- 预测区间为回归预测建模问题提供不确定性度量。
- 如何为标准回归问题开发和评估简单的多层感知器神经网络。
- 如何使用神经网络模型集成来计算和报告预测区间。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。




你好 Jason,
关于特征缩放的一个问题。
我需要特征缩放(例如标准化)吗?
– 逻辑回归
– ARIMA/ SARIMA/ SARIMAX?
谢谢,
Marco
是的,这是一个好主意。评估你的模型是否需要缩放,然后比较结果。
你好 Jason,
ARIMA/ SARIMA/ SARIMAX 与 Prophet 的优点是什么?
何时使用它们的建议?
当我有多个特征时,我是否必须使用 SARIMAX?
谢谢
Marco
它们都解决了略有不同的问题,这解释了
https://machinelearning.org.cn/time-series-forecasting-methods-in-python-cheat-sheet/
嗨,Jason,
点预测是从哪里输入的?模型是如何设置的,用来告诉它在哪里预测下一个数字?
通过调用 model.predict() 进行预测,如果这是个新想法,那么这可能有所帮助
https://machinelearning.org.cn/how-to-make-classification-and-regression-predictions-for-deep-learning-models-in-keras/
再次感谢 Jason 的精彩文章。关于已完成的示例,有两点:
* 在实际用例中,如果数据集足够大,我会将集成模型拟合到训练数据集的子集上,而不是整个数据集,你同意吗?
* 关于高斯方法与 bootstrap 方法的比较:在使用高斯方法时,对于每一轮,最好检查 yhat 值是否符合正态分布(例如,通过 Shapiro-Wilk 检验);否则,bootstrap 方法不假设正态分布(尽管此方法可能在计算上成本很高)
对这两点有什么建议吗?
不客气。
不,你会用子集进行装袋集成以提高技能。我们这里只关注减少预测的方差并捕捉可能的预测区间。如果你愿意,可以这样做,但这不一样。
Bootstrap 在计算上成本很高(每次预测一个?),但确实可以。Bootstrap 的优点是我们不必假设分布,我们只使用中位数和百分位数。
另一种技术是蒙特卡洛 Dropout,它只是在推理期间激活 dropout。你运行 100 次推理,就可以从单个模型中获得预测分布。来自这篇论文:https://arxiv.org/pdf/1506.02142.pdf
感谢您的建议!
为什么不直接为神经网络设置两个输出?一个输出均值,另一个输出对数方差(以避免负数)。假设是正态分布,您就有了计算分布所需的一切。
还有 dropout 方法,但我更喜欢变体推理方法
有趣的建议,尽管训练数据中的方差在所有情况下都为 0.0。
我不确定我是否理解为什么所有情况下的方差都是 0。这是直接的均值方差估计。类似于混合密度网络,但您只用修改后的损失函数和两个输出节点来求解均值和方差。
有道理。我曾认为每个点预测都是一个单独的条件概率分布。
嗨!您如何看待这里提出的方法?(适用于 Python 和 R)
https://thierrymoudiki.github.io/blog/2020/12/04/r/quasirandomizednn/bayesian-forecasting
也许您可以概括一下?
nnetsauce 通过准随机“神经网络”(参见 https://techtonique.github.io/nnetsauce/)进行统计/机器学习。在这个与时间序列相关的特定示例中(可以适应到表格数据),预测值中添加了一个“可信”区间。
感谢分享。
很好的例子。在实验物理和天文学中,人们几乎总是需要处理有噪声的输入和有噪声的输出。有些人已经考虑了在这种情况下的神经网络回归问题。请看这里:https://www.researchgate.net/publication/220540561_Neural_Network_Modelling_with_Input_Uncertainty_Theory_and_Application
有一个包含实际世界回归问题和不确定性的示例代码会很有用。
感谢您的建议!
嗨 Jason,感谢您的精彩教程。我有一个关于 predict with pi 函数的问题。我明白该函数设计为接受单行输入。我该如何将其更改为接受多行输入?非常感谢您的帮助。
您可以根据需要修改该函数,很抱歉我没有能力为您修改。
嗨 Jason,很棒的教程。我想知道您对如何衡量哪种不确定性估计方法“更好”有什么想法?例如,如果您有这种集成方法,与 dropout 相比,或者与上面提出的变分推理方法相比,您会如何选择您更喜欢哪种(假设预测误差恒定)?
我们可能希望在整个测试集上总不确定性尽可能低,但所有预测都落在区间内?
是的,但我猜这取决于你的目标以及数据和模型的具体情况。
也许您可以查阅一下比较方法优缺点的文献。
嗨,很好的例子!我对您提到的使用 bootstrap 方法来训练每个集成模型很感兴趣。
在这个例子中,当您构建模型集成时,您使用完全相同的数据集(本身是整个数据集的一个子集)来训练每个模型。例如,如果我有一个包含 100 个样本的数据集,并且我想用整个数据集的 70% 来训练我的集成模型,但我想使用 bootstrap 方法,您是建议使用与每个模型完全相同的 70 个样本进行训练数据 bootstrap,还是在整个数据集上进行 bootstrap,但为每个模型生成 70 个样本的训练集大小?在第一种情况下,我将能够向网络输入绝对未见过的数据,但第二种情况可能并非如此。您对此有什么建议吗?
嗨 Charlotte…非常欢迎!在使用 bootstrap 方法训练集成模型时,目标是创建数据集的多样化子集来训练集成中的每个模型,这可以提高泛化能力和鲁棒性。让我们分解一下您提到的两种方法,并讨论它们的影响。
### 1. 对每个模型使用完全相同的 70 个样本进行 Bootstrap
在这种方法中,您首先从 100 个样本的数据集中选择一个 70 个样本的子集,并使用这些完全相同的 70 个样本来训练集成中的每个模型。
**优点:**
– 模型之间训练数据的⼀致性。
– 训练数据和测试数据之间有清晰的分割,因为剩余的 30 个样本对于任何模型都是绝对未见过的。
**缺点:**
– 每个模型的训练数据缺乏多样性,这可能会降低集成的有效性。模型之间可能过于相似,因此无法提供完整的集成学习优势。
### 2. 在整个数据集上进行 Bootstrap,为每个模型生成 70 个样本的训练集大小
在这种方法中,您将为集成中的每个模型从整个 100 个样本的数据集中生成不同的 bootstrap 样本(有放回抽样),大小为 70。这意味着每个模型可能会看到一些样本多次,而一些样本可能完全不包含。
**优点:**
– 每个模型的训练数据具有多样性,这通常可以提高泛化能力。
– 每个模型都在不同的数据子集上进行训练,这有助于减少过拟合。
**缺点:**
– 训练数据中的一些样本也可能出现在测试数据中,这可能导致评估中的轻微偏差。
### 建议
为了实现训练多样性和评估完整性之间的最佳平衡,请考虑以下方法:
1. **生成用于训练的 Bootstrap 样本**:使用 bootstrap 为集成中的每个模型从整个数据集中创建不同的 70 个样本的子集。这确保了训练数据的多样性。
2. **维护一个单独的验证集**:保留一个单独的验证集或测试集,该集不用于训练任何模型。此集仅用于评估目的。在您的情况下,这将是剩余的 30 个样本。
这种方法使您能够利用 bootstrap 提供的多样性,同时确保您的评估指标可靠且基于未见过的数据。
### Python 代码示例
这是您如何在 Python 中使用 scikit-learn 和 NumPy 实现此方法:
pythonimport numpy as np
from sklearn.utils import resample
from sklearn.ensemble import BaggingClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score
# 示例数据集
X = np.random.rand(100, 5) # 100 个样本,5 个特征
y = np.random.randint(0, 2, 100) # 二元目标
# 分离一个验证集
validation_size = 30
X_train, X_val = X[:-validation_size], X[-validation_size:]
y_train, y_val = y[:-validation_size], y[-validation_size:]
# Bootstrap 样本/模型的数量
n_models = 10
# 初始化集成模型
ensemble_models = []
for _ in range(n_models)
# 生成一个 bootstrap 样本
X_bootstrap, y_bootstrap = resample(X_train, y_train, n_samples=70)
# 在 bootstrap 样本上训练模型(例如,决策树)
model = DecisionTreeClassifier()
model.fit(X_bootstrap, y_bootstrap)
# 存储训练好的模型
ensemble_models.append(model)
# 在验证集上进行预测
predictions = np.zeros((len(y_val), n_models))
for i, model in enumerate(ensemble_models)
predictions[:, i] = model.predict(X_val)
# 聚合预测(多数投票)
final_predictions = np.round(np.mean(predictions, axis=1))
# 评估集成模型
accuracy = accuracy_score(y_val, final_predictions)
print(f'验证精度: {accuracy:.2f}')
### 代码解释
1. **分离验证集**:我们将最后 30 个样本分离为验证集,确保它们不用于训练。
2. **Bootstrap 样本**:对于每个模型,我们从训练数据中生成一个大小为 70 的 bootstrap 样本。
3. **训练模型**:每个 bootstrap 样本用于训练不同的模型。
4. **集成预测**:使用多数投票聚合每个模型的预测。
5. **在验证集上评估**:在验证集上计算最终精度。
通过遵循此方法,您可以利用 bootstrap 的优势,同时保持训练和验证数据之间的严格分离,从而确保可靠的评估指标。
嗨 James,非常感谢,这非常有帮助!