主成分分析(PCA)是一种无监督机器学习技术。主成分分析最常见的用途可能是降维。除了将PCA用作数据预处理技术外,我们还可以使用它来帮助可视化数据。一图胜千言。通过对数据进行可视化,我们可以更容易地获得一些见解,并决定机器学习模型的下一步操作。
在本教程中,您将了解如何使用PCA可视化数据,以及如何使用可视化来帮助确定降维的参数。
完成本教程后,您将了解:
- 如何可视化高维数据
- PCA中的解释方差是什么
- 直观地观察高维数据PCA结果的解释方差
让我们开始吧。

用于可视化的主成分分析
照片来源:Levan Gokadze,保留部分权利。
教程概述
本教程分为两部分;它们是
- 高维数据的散点图
- 可视化解释的方差
先决条件
本教程假设您已熟悉以下内容:
高维数据的散点图
可视化是获取数据洞察的关键步骤。我们可以从可视化中了解到是否可以观察到模式,从而估计哪种机器学习模型是合适的。
二维绘图很容易。通常,带有x轴和y轴的散点图是二维的。三维绘图有点挑战性,但并非不可能。例如,在matplotlib中可以进行3D绘图。唯一的问题是,在纸上或屏幕上,我们一次只能查看一个视口或投影的三维图。在matplotlib中,这由仰角和方位角的度数控制。四维或五维绘图是不可能的,因为我们生活在三维世界中,对高维度的东西是什么样子毫无概念。
这就是PCA之类的降维技术派上用场的地方。我们可以将维度降低到二维或三维,以便进行可视化。让我们从一个例子开始。
我们从葡萄酒数据集开始,这是一个具有13个特征(即数据集是13维)和3个类别的数据集。有178个样本。
|
1 2 3 4 5 |
from sklearn.datasets import load_wine winedata = load_wine() X, y = winedata['data'], winedata['target'] print(X.shape) print(y.shape) |
|
1 2 |
(178, 13) (178,) |
在13个特征中,我们可以任意选择两个并使用matplotlib绘图(我们使用c参数为不同的类别着色)
|
1 2 3 4 |
... import matplotlib.pyplot as plt plt.scatter(X[:,1], X[:,2], c=y) plt.show() |
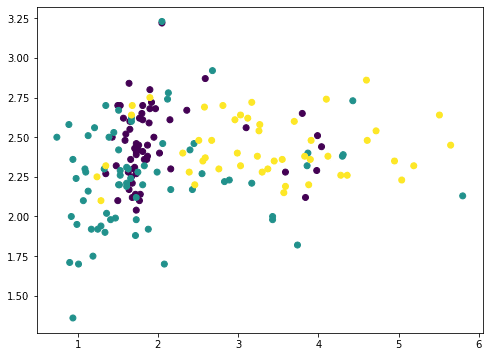
或者我们也可以任意选择三个并以3D显示
|
1 2 3 4 |
... ax = fig.add_subplot(projection='3d') ax.scatter(X[:,1], X[:,2], X[:,3], c=y) plt.show() |
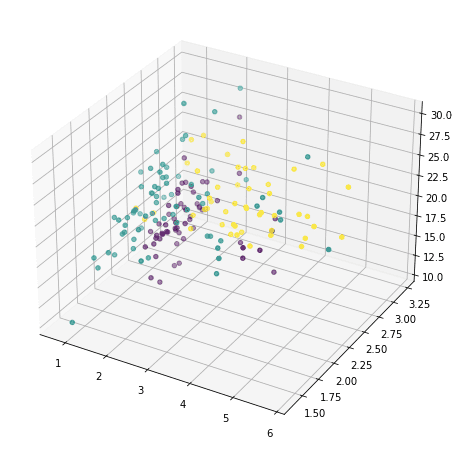
但这并没有揭示数据的多少信息,因为大部分特征都没有显示出来。我们现在求助于主成分分析。
|
1 2 3 4 5 6 7 |
... 从 sklearn.分解 导入 PCA pca = PCA() Xt = pca.fit_transform(X) plot = plt.scatter(Xt[:,0], Xt[:,1], c=y) plt.legend(handles=plot.legend_elements()[0], labels=list(winedata['target_names'])) plt.show() |
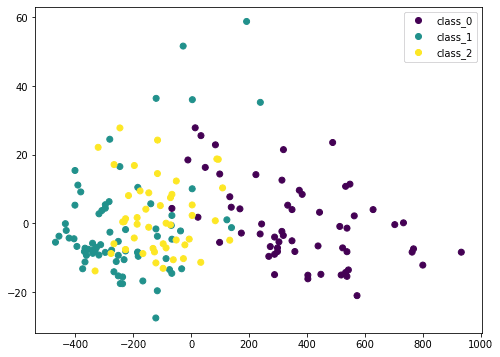
在这里,我们将输入数据X通过PCA转换为Xt。我们只考虑前两列,它们包含最多的信息,并将其二维绘制。我们可以看到紫色类别非常明显,但仍然存在一些重叠。如果我们对数据进行PCA之前的缩放,结果会有所不同。
|
1 2 3 4 5 6 7 8 9 |
... from sklearn.preprocessing import StandardScaler from sklearn.pipeline import Pipeline pca = PCA() pipe = Pipeline([('scaler', StandardScaler()), ('pca', pca)]) Xt = pipe.fit_transform(X) plot = plt.scatter(Xt[:,0], Xt[:,1], c=y) plt.legend(handles=plot.legend_elements()[0], labels=list(winedata['target_names'])) plt.show() |
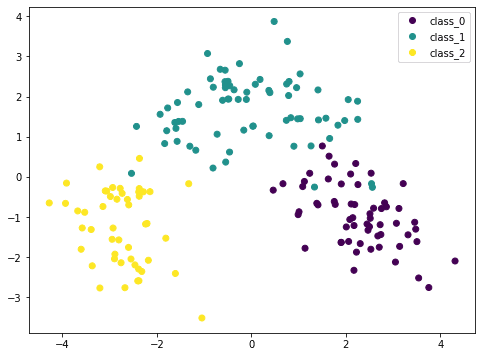
由于PCA对缩放敏感,如果我们使用StandardScaler对每个特征进行归一化,我们可以看到更好的结果。这里的不同类别更加明显。通过查看此图,我们可以确信像SVM这样的简单模型可以以高精度对该数据集进行分类。
总而言之,以下是生成可视化代码的全部内容:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 |
from sklearn.datasets import load_wine 从 sklearn.分解 导入 PCA from sklearn.preprocessing import StandardScaler from sklearn.pipeline import Pipeline import matplotlib.pyplot as plt # 加载数据集 winedata = load_wine() X, y = winedata['data'], winedata['target'] print("X shape:", X.shape) print("y shape:", y.shape) # 显示任意两个特征 plt.figure(figsize=(8,6)) plt.scatter(X[:,1], X[:,2], c=y) plt.xlabel(winedata["feature_names"][1]) plt.ylabel(winedata["feature_names"][2]) plt.title("Two particular features of the wine dataset") plt.show() # 显示任意三个特征 fig = plt.figure(figsize=(10,8)) ax = fig.add_subplot(projection='3d') ax.scatter(X[:,1], X[:,2], X[:,3], c=y) ax.set_xlabel(winedata["feature_names"][1]) ax.set_ylabel(winedata["feature_names"][2]) ax.set_zlabel(winedata["feature_names"][3]) ax.set_title("Three particular features of the wine dataset") plt.show() # 未经缩放显示前两个主成分 pca = PCA() plt.figure(figsize=(8,6)) Xt = pca.fit_transform(X) plot = plt.scatter(Xt[:,0], Xt[:,1], c=y) plt.legend(handles=plot.legend_elements()[0], labels=list(winedata['target_names'])) plt.xlabel("PC1") plt.ylabel("PC2") plt.title("First two principal components") plt.show() # 缩放后显示前两个主成分 pca = PCA() pipe = Pipeline([('scaler', StandardScaler()), ('pca', pca)]) plt.figure(figsize=(8,6)) Xt = pipe.fit_transform(X) plot = plt.scatter(Xt[:,0], Xt[:,1], c=y) plt.legend(handles=plot.legend_elements()[0], labels=list(winedata['target_names'])) plt.xlabel("PC1") plt.ylabel("PC2") plt.title("First two principal components after scaling") plt.show() |
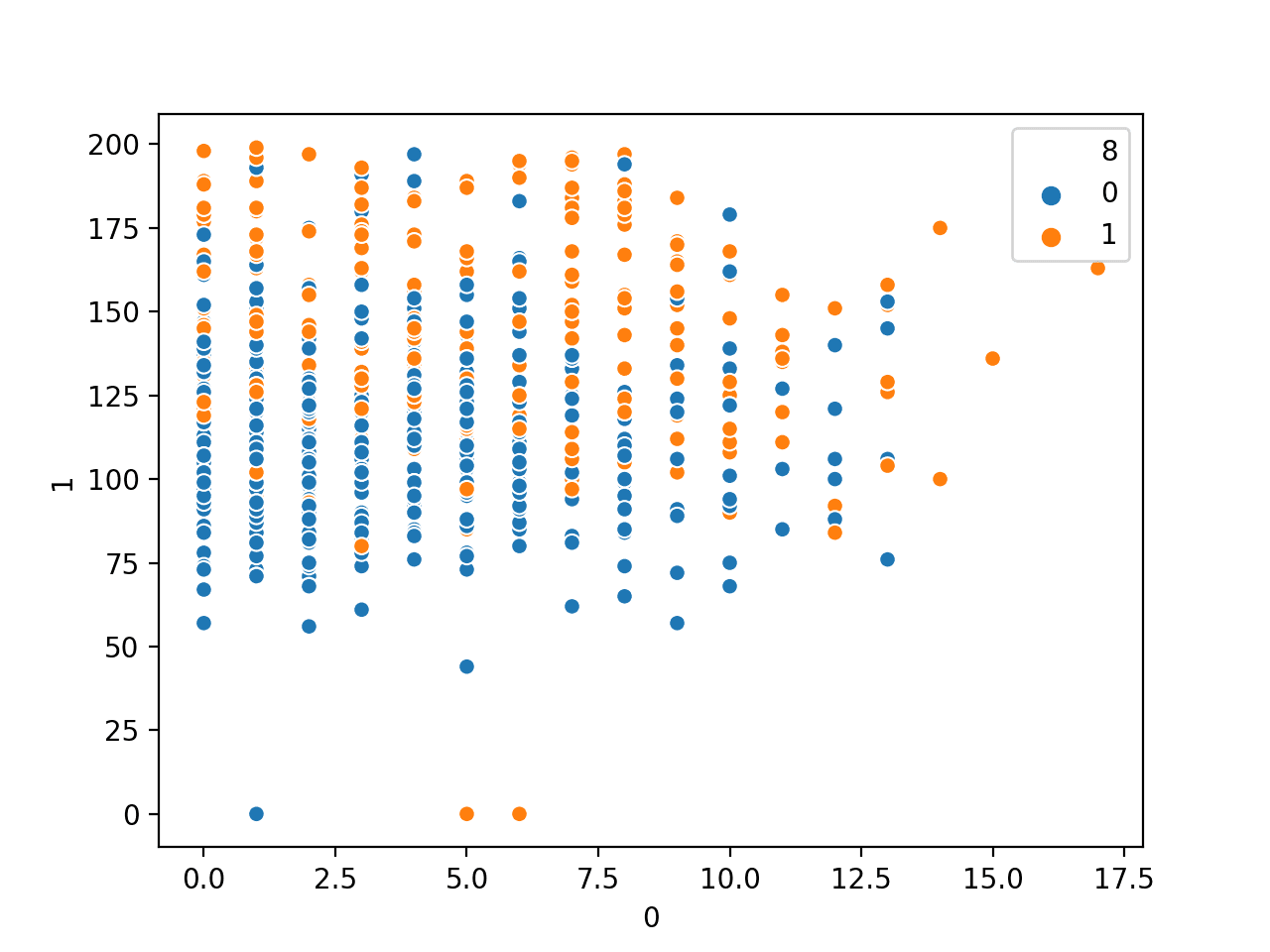
如果我们在不同的数据集上应用相同的方法,例如MINST手写数字,散点图不会显示出明显的边界,因此需要更复杂的模型(如神经网络)来进行分类。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
from sklearn.datasets import load_digits 从 sklearn.分解 导入 PCA from sklearn.preprocessing import StandardScaler from sklearn.pipeline import Pipeline import matplotlib.pyplot as plt digitsdata = load_digits() X, y = digitsdata['data'], digitsdata['target'] pca = PCA() pipe = Pipeline([('scaler', StandardScaler()), ('pca', pca)]) plt.figure(figsize=(8,6)) Xt = pipe.fit_transform(X) plot = plt.scatter(Xt[:,0], Xt[:,1], c=y) plt.legend(handles=plot.legend_elements()[0], labels=list(digitsdata['target_names'])) plt.show() |
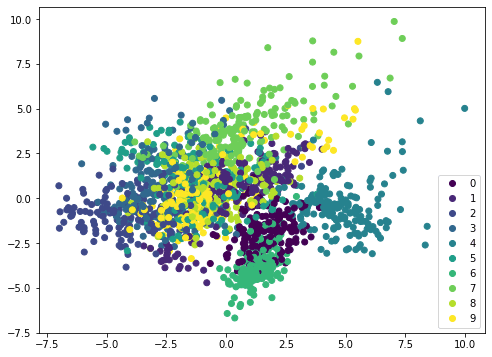
可视化解释的方差
PCA本质上是通过线性组合来重新排列特征。因此,它被称为特征提取技术。PCA的一个特征是第一个主成分包含有关数据集的最多信息。第二个主成分比第三个更具信息量,依此类推。
为了说明这一点,我们可以逐步从原始数据集中删除主成分,看看数据集的样子。让我们考虑一个特征较少的数据集,并在图中显示两个特征。
|
1 2 3 4 5 6 |
from sklearn.datasets import load_iris irisdata = load_iris() X, y = irisdata['data'], irisdata['target'] plt.figure(figsize=(8,6)) plt.scatter(X[:,0], X[:,1], c=y) plt.show() |
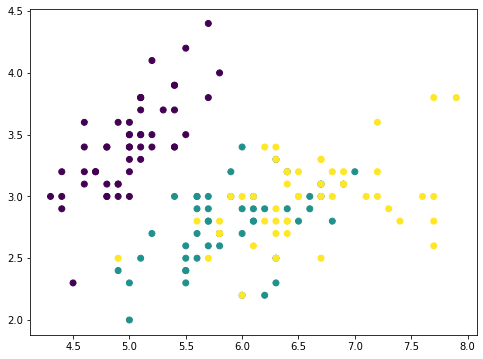
这是鸢尾花数据集,它只有四个特征。特征的尺度是可比的,因此我们可以跳过缩放器。对于具有4个特征的数据,PCA最多可以产生4个主成分。
|
1 2 3 |
... pca = PCA().fit(X) print(pca.components_) |
|
1 2 3 4 |
[[ 0.36138659 -0.08452251 0.85667061 0.3582892 ] [ 0.65658877 0.73016143 -0.17337266 -0.07548102] [-0.58202985 0.59791083 0.07623608 0.54583143] [-0.31548719 0.3197231 0.47983899 -0.75365743]] |
例如,第一行是创建第一个主成分的主轴。对于任何具有特征$p=(a,b,c,d)$的数据点$p$,由于主轴由向量$v=(0.36,-0.08,0.86,0.36)$表示,则该数据点的第一个主成分在该主轴上的值为$0.36 \times a – 0.08 \times b + 0.86 \times c + 0.36\times d$。使用向量点积,该值可以表示为:
$$
p \cdot v
$$
因此,对于数据集$X$(一个150×4的矩阵,150个数据点,每个有4个特征),我们可以通过矩阵向量乘法将每个数据点映射到该主轴上的值:
$$
X \cdot v
$$
结果是一个长度为150的向量。现在,如果我们从每个数据点中减去沿主轴向量的相应值,那将是:
$$
X – (X \cdot v) \cdot v^T
$$
其中转置向量$v^T$是一行,$X\cdot v$是一列。乘积$(X \cdot v) \cdot v^T$遵循矩阵-矩阵乘法,结果是一个$150\times 4$的矩阵,与$X$维度相同。
如果我们绘制$(X \cdot v) \cdot v^T$的前两个特征,它看起来像这样:
|
1 2 3 4 5 6 7 8 |
... # 移除PC1 Xmean = X - X.mean(axis=0) value = Xmean @ pca.components_[0] pc1 = value.reshape(-1,1) @ pca.components_[0].reshape(1,-1) Xremove = X - pc1 plt.scatter(Xremove[:,0], Xremove[:,1], c=y) plt.show() |
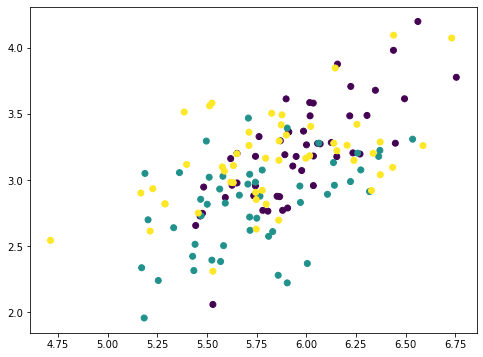
numpy数组Xmean用于将X的特征移至以零为中心。这是PCA所必需的。然后通过矩阵向量乘法计算数组value。
数组value是每个数据点映射到主轴上的幅度。因此,如果我们将其乘以主轴向量,我们将得到一个数组pc1。将其从原始数据集X中减去,我们得到一个新数组Xremove。在图中,我们观察到散点图上的点挤在一起,每个类别的簇都不如之前明显。这意味着我们通过删除第一个主成分移除了大量信息。如果我们再次重复此过程,点将进一步挤压。
|
1 2 3 4 5 6 7 |
... # 移除PC2 value = Xmean @ pca.components_[1] pc2 = value.reshape(-1,1) @ pca.components_[1].reshape(1,-1) Xremove = Xremove - pc2 plt.scatter(Xremove[:,0], Xremove[:,1], c=y) plt.show() |
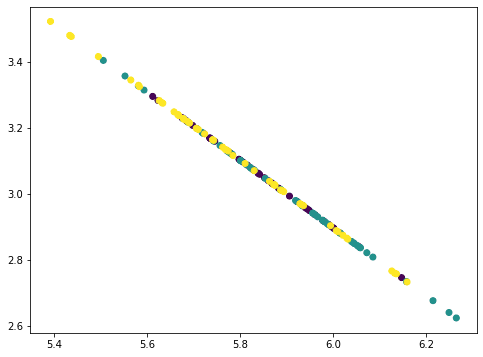
这看起来像一条直线,但实际上不是。如果我们再重复一次,所有的点都会坍缩成一条直线。
|
1 2 3 4 5 6 7 |
... # 移除PC3 value = Xmean @ pca.components_[2] pc3 = value.reshape(-1,1) @ pca.components_[2].reshape(1,-1) Xremove = Xremove - pc3 plt.scatter(Xremove[:,0], Xremove[:,1], c=y) plt.show() |
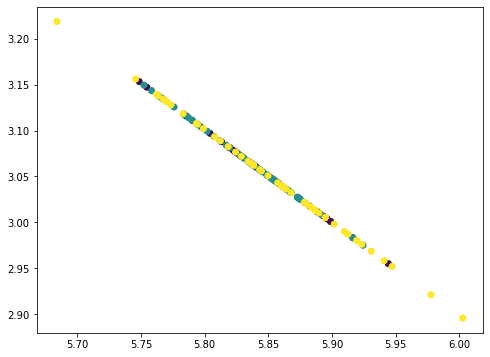
由于我们从数据中移除了三个主成分,而数据只有四个特征,因此所有的点都落在一条直线上。因此,我们的数据矩阵的**秩为1**。您可以尝试再次执行此过程,结果将是所有点都坍缩成一个点。通过我们逐步移除主成分移除的信息量可以通过PCA的相应**解释方差比**找到。
|
1 2 |
... print(pca.explained_variance_ratio_) |
|
1 |
[0.92461872 0.05306648 0.01710261 0.00521218] |
在这里我们可以看到,第一个分量解释了92.5%的方差,第二个分量解释了5.3%的方差。如果我们移除了前两个主成分,剩余的方差只有2.2%,因此在视觉上,移除两个分量后的图看起来像一条直线。事实上,当我们与上面的图进行比较时,我们不仅看到点被压缩了,而且在移除分量时,x轴和y轴的范围也变小了。
就机器学习而言,我们可以考虑仅使用一个特征来对该数据集进行分类,即第一个主成分。我们应该期望在达到90%的原始准确率时,与使用全部特征集相比。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
... from sklearn.model_selection import train_test_split from sklearn.metrics import f1_score from collections import Counter from sklearn.svm import SVC X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33) clf = SVC(kernel="linear", gamma='auto').fit(X_train, y_train) print("Using all features, accuracy: ", clf.score(X_test, y_test)) print("Using all features, F1: ", f1_score(y_test, clf.predict(X_test), average="macro")) mean = X_train.mean(axis=0) X_train2 = X_train - mean X_train2 = (X_train2 @ pca.components_[0]).reshape(-1,1) clf = SVC(kernel="linear", gamma='auto').fit(X_train2, y_train) X_test2 = X_test - mean X_test2 = (X_test2 @ pca.components_[0]).reshape(-1,1) print("Using PC1, accuracy: ", clf.score(X_test2, y_test)) print("Using PC1, F1: ", f1_score(y_test, clf.predict(X_test2), average="macro")) |
|
1 2 3 4 |
使用所有特征,准确率: 1.0 使用所有特征,F1: 1.0 使用PC1,准确率: 0.96 使用PC1,F1: 0.9645191409897292 |
解释方差的另一个用途是压缩。鉴于第一个主成分的解释方差很大,如果我们需要存储数据集,我们只需存储第一个主轴上的投影值($X\cdot v$)以及主轴的向量$v$。然后,我们可以通过将它们相乘来近似重构原始数据集。
$$
X \approx (X\cdot v) \cdot v^T
$$
这样,我们只需要为每个数据点存储一个值,而不是四个特征的四个值。如果我们存储多个主轴上的投影值并将多个主成分相加,近似值会更准确。
总而言之,以下是生成可视化代码的全部内容:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 |
from sklearn.datasets import load_iris from sklearn.model_selection import train_test_split 从 sklearn.分解 导入 PCA from sklearn.metrics import f1_score from sklearn.svm import SVC import matplotlib.pyplot as plt # 加载鸢尾花数据集 irisdata = load_iris() X, y = irisdata['data'], irisdata['target'] plt.figure(figsize=(8,6)) plt.scatter(X[:,0], X[:,1], c=y) plt.xlabel(irisdata["feature_names"][0]) plt.ylabel(irisdata["feature_names"][1]) plt.title("Two features from the iris dataset") plt.show() # 显示主成分 pca = PCA().fit(X) print("Principal components:") print(pca.components_) # 移除PC1 Xmean = X - X.mean(axis=0) value = Xmean @ pca.components_[0] pc1 = value.reshape(-1,1) @ pca.components_[0].reshape(1,-1) Xremove = X - pc1 plt.figure(figsize=(8,6)) plt.scatter(Xremove[:,0], Xremove[:,1], c=y) plt.xlabel(irisdata["feature_names"][0]) plt.ylabel(irisdata["feature_names"][1]) plt.title("Two features from the iris dataset after removing PC1") plt.show() # 移除PC2 Xmean = X - X.mean(axis=0) value = Xmean @ pca.components_[1] pc2 = value.reshape(-1,1) @ pca.components_[1].reshape(1,-1) Xremove = Xremove - pc2 plt.figure(figsize=(8,6)) plt.scatter(Xremove[:,0], Xremove[:,1], c=y) plt.xlabel(irisdata["feature_names"][0]) plt.ylabel(irisdata["feature_names"][1]) plt.title("Two features from the iris dataset after removing PC1 and PC2") plt.show() # 移除PC3 Xmean = X - X.mean(axis=0) value = Xmean @ pca.components_[2] pc3 = value.reshape(-1,1) @ pca.components_[2].reshape(1,-1) Xremove = Xremove - pc3 plt.figure(figsize=(8,6)) plt.scatter(Xremove[:,0], Xremove[:,1], c=y) plt.xlabel(irisdata["feature_names"][0]) plt.ylabel(irisdata["feature_names"][1]) plt.title("Two features from the iris dataset after removing PC1 to PC3") plt.show() # 打印解释方差比 print("Explainedd variance ratios:") print(pca.explained_variance_ratio_) # 拆分数据 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33) # 在所有特征上运行分类器 clf = SVC(kernel="linear", gamma='auto').fit(X_train, y_train) print("Using all features, accuracy: ", clf.score(X_test, y_test)) print("Using all features, F1: ", f1_score(y_test, clf.predict(X_test), average="macro")) # 在PC1上运行分类器 mean = X_train.mean(axis=0) X_train2 = X_train - mean X_train2 = (X_train2 @ pca.components_[0]).reshape(-1,1) clf = SVC(kernel="linear", gamma='auto').fit(X_train2, y_train) X_test2 = X_test - mean X_test2 = (X_test2 @ pca.components_[0]).reshape(-1,1) print("Using PC1, accuracy: ", clf.score(X_test2, y_test)) print("Using PC1, F1: ", f1_score(y_test, clf.predict(X_test2), average="macro")) |
延伸阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
书籍
教程
API
总结
在本教程中,您学习了如何使用主成分分析可视化数据。
具体来说,你学到了:
- 使用PCA将高维数据集可视化为2D
- 如何使用PCA中的绘图来帮助选择合适的机器学习模型
- 如何观察PCA的解释方差比
- 解释方差比对机器学习的意义




你好,当我尝试从这个路径导入自己的数据集而不是默认数据集时,我遇到了这个错误。
ImportError 回溯 (最近一次调用)
in
—-> 1 from sklearn.datasets import cleveland_data
2 winedata = cleveland_data()
3 X, y = winedata[‘data’], winedata[‘target’]
4 print(X.shape)
5 print(y.shape)
ImportError: cannot import name ‘cleveland_data’ from ‘sklearn.datasets’ (/opt/anaconda3/lib/python3.8/site-packages/sklearn/datasets/__init__.py)
那意味着你的scikit-learn中没有cleveland_data。事实上,最新的文档中也没有提及。
谢谢你,Adrian!