随机森林是一种集成机器学习算法。
鉴于它在广泛的分类和回归预测建模问题上都表现良好或出色,它可能是最流行和最广泛使用的机器学习算法。
它也很容易使用,因为它只有少数几个关键的超参数,并且这些超参数的配置有合理的启发式方法。
在本教程中,您将学习如何为分类和回归开发随机森林集成模型。
完成本教程后,您将了解:
- 随机森林集成是决策树的集成,也是装袋(bagging)的自然延伸。
- 如何使用 scikit-learn 进行分类和回归的随机森林集成。
- 如何探究随机森林模型超参数对模型性能的影响。
通过我的新书《使用 Python 的集成学习算法》启动您的项目,包括分步教程和所有示例的 Python 源代码文件。
让我们开始吧。
- 2020 年 8 月更新:新增了一个常见问题部分。

如何在 Python 中开发随机森林集成模型
照片由 Sheila Sund 拍摄,保留部分权利。
教程概述
本教程分为四个部分;它们是
- 随机森林算法
- 随机森林 Scikit-Learn API
- 用于分类的随机森林
- 用于回归的随机森林
- 随机森林超参数
- 探索样本数量
- 探索特征数量
- 探索树的数量
- 探索树深度
- 常见问题
随机森林算法
随机森林是决策树算法的集成。
它是决策树的自助聚合(bagging)的扩展,可用于分类和回归问题。
在装袋中,创建多个决策树,其中每个树都是从训练数据集的不同引导样本创建的。 引导样本是训练数据集的样本,其中一个样本可以在样本中出现多次,这被称为有放回抽样。
装袋是一种有效的集成算法,因为每个决策树都是在略有不同的训练数据集上拟合的,因此性能也略有不同。与常规决策树模型(例如分类和回归树(CART))不同,集成中使用的树是未修剪的,这使得它们对训练数据集略有过拟合。这是可取的,因为它有助于使每个树更不同,并且预测或预测误差的相关性更小。
来自树的预测在所有决策树上进行平均,从而获得比模型中任何单个树更好的性能。
然后,集成中的每个模型都用于生成新样本的预测,并将这 m 个预测进行平均,以得出森林的预测。
— 第 199 页,应用预测建模,2013 年。
回归问题的预测是集成中所有树的预测的平均值。分类问题的预测是集成中所有树的类别标签的多数投票。
- 回归:预测是所有决策树的平均预测。
- 分类:预测是所有决策树预测的多数投票类别标签。
与装袋一样,森林中的每棵树都对新样本的分类进行投票,并且集成中每个类别的投票比例就是预测概率向量。
— 第 387 页,应用预测建模,2013 年。
随机森林涉及从训练数据集的引导样本中构建大量决策树,类似于装袋。
与装袋不同,随机森林还涉及在树的构建过程中在每个分裂点选择输入特征(列或变量)的子集。通常,构建决策树涉及评估数据中每个输入变量的值,以便选择一个分裂点。通过将特征减少到在每个分裂点可以考虑的随机子集,它迫使集成中的每个决策树更加不同。
随机森林通过一个小的调整来解耦树,从而改进了装袋树。[...] 但是在构建这些决策树时,每次考虑树中的分裂时,都会从 p 个预测变量的完整集合中随机选择 m 个预测变量作为分裂候选者。
— 第 320 页,使用 R 的统计学习导论与应用,2014 年。
其结果是,集成中每棵树所做的预测以及随后的预测误差更加不同或相关性更低。当这些相关性较低的树的预测被平均以进行预测时,它通常比装袋决策树产生更好的性能。
随机森林最重要的超参数之一可能是在每个分裂点要考虑的随机特征的数量。
随机森林的调优参数是在每个分裂点选择的随机选择的预测变量 k 的数量,通常称为 mtry。在回归环境中,Breiman (2001) 建议将 mtry 设置为预测变量数量的三分之一。
— 第 199 页,应用预测建模,2013 年。
对于回归问题,一个好的启发式方法是将此超参数设置为输入特征数量的 1/3。
- num_features_for_split = total_input_features / 3
对于分类问题,Breiman (2001) 建议将 mtry 设置为预测变量数量的平方根。
— 第 387 页,应用预测建模,2013 年。
对于分类问题,一个好的启发式方法是将此超参数设置为输入特征数量的平方根。
- num_features_for_split = sqrt(total_input_features)
另一个重要的超参数是决策树的深度。更深的树通常对训练数据过拟合更严重,但也更不相关,这反过来可能会提高集成的性能。深度从 1 到 10 层可能有效。
最后,可以设置集成中决策树的数量。通常,会增加这个数量直到没有进一步的改进。
想开始学习集成学习吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
随机森林 Scikit-Learn API
随机森林集成可以从头开始实现,尽管对于初学者来说这可能具有挑战性。
scikit-learn Python 机器学习库提供了随机森林的实现,用于机器学习。
它在库的现代版本中可用。
首先,通过运行以下脚本确认您正在使用该库的现代版本
|
1 2 3 |
# 检查 scikit-learn 版本 import sklearn print(sklearn.__version__) |
运行脚本将打印您的 scikit-learn 版本。
您的版本应该相同或更高。如果不是,您必须升级您的 scikit-learn 库版本。
|
1 |
0.22.1 |
随机森林通过 RandomForestRegressor 和 RandomForestClassifier 类提供。
这两个模型的操作方式相同,并接受影响决策树创建方式的相同参数。
模型构建中使用了随机性。这意味着每次在相同数据上运行算法时,它都会生成一个略有不同的模型。
当使用具有随机学习算法的机器学习算法时,最好通过对它们的性能进行多次运行或重复的交叉验证来评估它们。在拟合最终模型时,可能需要增加树的数量,直到模型在重复评估中的方差减小,或者拟合多个最终模型并平均它们的预测。
让我们看看如何为分类和回归任务开发随机森林集成模型。
用于分类的随机森林
在本节中,我们将介绍如何将随机森林用于分类问题。
首先,我们可以使用 make_classification() 函数 创建一个包含 1,000 个示例和 20 个输入特征的合成二元分类问题。
完整的示例如下所示。
|
1 2 3 4 5 6 |
# 测试分类数据集 from sklearn.datasets import make_classification # 定义数据集 X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=3) # 汇总数据集 print(X.shape, y.shape) |
运行示例会创建数据集并总结输入和输出组件的形状。
|
1 |
(1000, 20) (1000,) |
接下来,我们可以在此数据集上评估随机森林算法。
我们将使用重复分层 k 折交叉验证评估模型,重复 3 次,折叠 10 次。我们将报告模型在所有重复和折叠中的准确性的均值和标准差。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
# evaluate random forest algorithm for classification from numpy import mean from numpy import std from sklearn.datasets import make_classification from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.ensemble import RandomForestClassifier # 定义数据集 X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=3) # 定义模型 model = RandomForestClassifier() # 评估模型 cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) n_scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1, error_score='raise') # 报告表现 print('Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores))) |
运行示例报告了模型的平均准确度和标准差。
注意:您的结果可能会有所不同,因为算法或评估过程的随机性,或数值精度上的差异。请考虑多次运行示例并比较平均结果。
在这种情况下,我们可以看到默认超参数的随机森林集成模型达到了大约 90.5% 的分类准确率。
|
1 |
准确度:0.905 (0.025) |
我们还可以将随机森林模型用作最终模型,并进行分类预测。
首先,随机森林集成模型在所有可用数据上进行拟合,然后可以调用 predict() 函数来对新数据进行预测。
以下示例在我们的二元分类数据集上演示了这一点。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
# 使用随机森林进行分类预测 from sklearn.datasets import make_classification from sklearn.ensemble import RandomForestClassifier # 定义数据集 X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=3) # 定义模型 model = RandomForestClassifier() # 在整个数据集上拟合模型 model.fit(X, y) # 进行单次预测 row = [[-8.52381793,5.24451077,-12.14967704,-2.92949242,0.99314133,0.67326595,-0.38657932,1.27955683,-0.60712621,3.20807316,0.60504151,-1.38706415,8.92444588,-7.43027595,-2.33653219,1.10358169,0.21547782,1.05057966,0.6975331,0.26076035]] yhat = model.predict(row) print('Predicted Class: %d' % yhat[0]) |
运行示例会拟合整个数据集上的随机森林集成模型,然后将其用于对新数据行进行预测,就像我们在应用程序中使用模型时一样。
|
1 |
预测类别:0 |
现在我们已经熟悉了如何使用随机森林进行分类,接下来让我们看看回归的 API。
用于回归的随机森林
在本节中,我们将探讨如何将随机森林用于回归问题。
首先,我们可以使用 make_regression() 函数 创建一个包含 1,000 个示例和 20 个输入特征的合成回归问题。
完整的示例如下所示。
|
1 2 3 4 5 6 |
# 测试回归数据集 from sklearn.datasets import make_regression # 定义数据集 X, y = make_regression(n_samples=1000, n_features=20, n_informative=15, noise=0.1, random_state=2) # 汇总数据集 print(X.shape, y.shape) |
运行示例会创建数据集并总结输入和输出组件的形状。
|
1 |
(1000, 20) (1000,) |
接下来,我们可以在此数据集上评估随机森林算法。
与上一节一样,我们将使用重复的 k 折交叉验证评估模型,重复 3 次,折叠 10 次。我们将报告模型在所有重复和折叠中的平均绝对误差 (MAE)。scikit-learn 库将 MAE 设为负数,以便最大化而不是最小化。这意味着负数 MAE 越大越好,完美模型的 MAE 为 0。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
# 评估回归的随机森林集成 from numpy import mean from numpy import std from sklearn.datasets import make_regression from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedKFold from sklearn.ensemble import RandomForestRegressor # 定义数据集 X, y = make_regression(n_samples=1000, n_features=20, n_informative=15, noise=0.1, random_state=2) # 定义模型 model = RandomForestRegressor() # 评估模型 cv = RepeatedKFold(n_splits=10, n_repeats=3, random_state=1) n_scores = cross_val_score(model, X, y, scoring='neg_mean_absolute_error', cv=cv, n_jobs=-1, error_score='raise') # 报告表现 print('MAE: %.3f (%.3f)' % (mean(n_scores), std(n_scores))) |
运行示例会报告模型的平均 MAE 和标准差。
注意:您的结果可能会有所不同,因为算法或评估过程的随机性,或数值精度上的差异。请考虑多次运行示例并比较平均结果。
在这种情况下,我们可以看到具有默认超参数的随机森林集成模型实现了大约 90 的 MAE。
|
1 |
平均绝对误差:-90.149 (7.924) |
我们还可以将随机森林模型用作最终模型,并进行回归预测。
首先,随机森林集成模型在所有可用数据上进行拟合,然后可以调用 predict() 函数来对新数据进行预测。
以下示例在我们的回归数据集上演示了这一点。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
# 用于回归预测的随机森林 from sklearn.datasets import make_regression from sklearn.ensemble import RandomForestRegressor # 定义数据集 X, y = make_regression(n_samples=1000, n_features=20, n_informative=15, noise=0.1, random_state=2) # 定义模型 model = RandomForestRegressor() # 在整个数据集上拟合模型 model.fit(X, y) # 进行单次预测 row = [[-0.89483109,-1.0670149,-0.25448694,-0.53850126,0.21082105,1.37435592,0.71203659,0.73093031,-1.25878104,-2.01656886,0.51906798,0.62767387,0.96250155,1.31410617,-1.25527295,-0.85079036,0.24129757,-0.17571721,-1.11454339,0.36268268]] yhat = model.predict(row) print('Prediction: %d' % yhat[0]) |
运行示例会拟合整个数据集上的随机森林集成模型,然后将其用于对新数据行进行预测,就像我们在应用程序中使用模型时一样。
|
1 |
预测:-173 |
现在我们已经熟悉了如何使用 scikit-learn API 评估和使用随机森林集成模型,接下来我们来看看如何配置模型。
随机森林超参数
在本节中,我们将仔细研究一些您应该考虑为随机森林集成模型调整的超参数以及它们对模型性能的影响。
探索样本数量
集成中的每个决策树都是在从训练数据集抽取的自助样本上拟合的。
如果您需要,可以通过将“bootstrap”参数设置为 False 来关闭此功能。在这种情况下,整个训练数据集将用于训练每个决策树。不建议这样做。
“max_samples”参数可以设置为 0 到 1 之间的浮点数,以控制训练每个决策树的引导样本占训练数据集大小的百分比。
例如,如果训练数据集有 100 行,max_samples 参数可以设置为 0.5,那么每个决策树将使用 (100 * 0.5) 或 50 行数据的引导样本进行拟合。
较小的样本量会使树之间的差异更大,而较大的样本量会使树更相似。将 max_samples 设置为“None”将使样本量与训练数据集相同,这是默认值。
以下示例演示了从 10% 到 100% 的不同引导样本量对随机森林算法性能的影响。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 |
# 探索随机森林引导样本量对性能的影响 from numpy import mean from numpy import std from numpy import arange from sklearn.datasets import make_classification from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.ensemble import RandomForestClassifier from matplotlib import pyplot # 获取数据集 定义 获取_数据集(): X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=3) 返回 X, y # 获取要评估的模型列表 定义 获取_模型(): models = dict() # 探索从 10% 到 100% 的比率,以 10% 为增量 for i in arange(0.1, 1.1, 0.1): key = '%.1f' % i # 设置 max_samples=None 表示使用 100% if i == 1.0: i = None models[key] = RandomForestClassifier(max_samples=i) 返回 模型 # 使用交叉验证评估给定模型 def evaluate_model(model, X, y): # 定义评估过程 cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) # 评估模型并收集结果 scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1) 返回 分数 # 定义数据集 X, y = get_dataset() # 获取要评估的模型 模型 = 获取_模型() # 评估模型并存储结果 results, names = list(), list() for name, model in models.items(): # 评估模型 scores = evaluate_model(model, X, y) # 存储结果 results.append(scores) names.append(name) # 沿途总结性能 print('>%s %.3f (%.3f)' % (name, mean(scores), std(scores))) # 绘制模型性能以供比较 pyplot.boxplot(results, labels=names, showmeans=True) pyplot.show() |
运行示例首先报告每个数据集大小的平均准确率。
注意:您的结果可能会有所不同,因为算法或评估过程的随机性,或数值精度上的差异。请考虑多次运行示例并比较平均结果。
在这种情况下,结果表明使用与训练数据集大小相同的引导样本量可以在此数据集上获得最佳结果。
这是默认设置,在大多数情况下应该使用它。
|
1 2 3 4 5 6 7 8 9 10 |
>10 0.856 (0.031) >20 0.873 (0.029) >30 0.881 (0.021) >40 0.891 (0.033) >50 0.893 (0.025) >60 0.897 (0.030) >70 0.902 (0.024) >80 0.903 (0.024) >90 0.900 (0.026) >100 0.903 (0.027) |
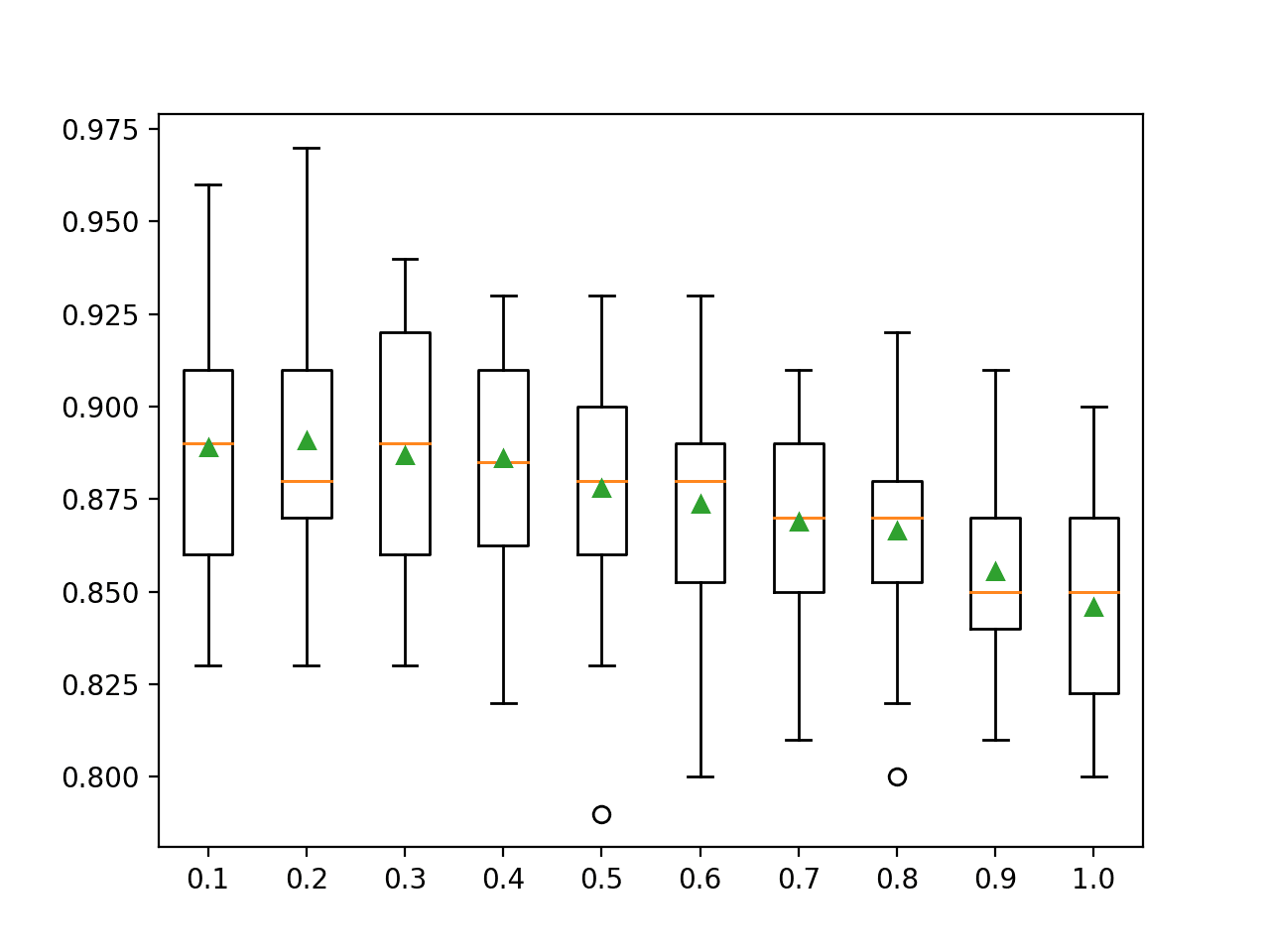
为每个引导样本量的准确率分布创建了箱线图。
在这种情况下,我们可以看到一个普遍趋势,即样本越大,模型的性能越好。
您可能希望扩展此示例,看看如果引导样本量大于甚至远大于训练数据集(例如,您可以将整数值设置为样本数,而不是训练数据集大小的浮点百分比)会发生什么。
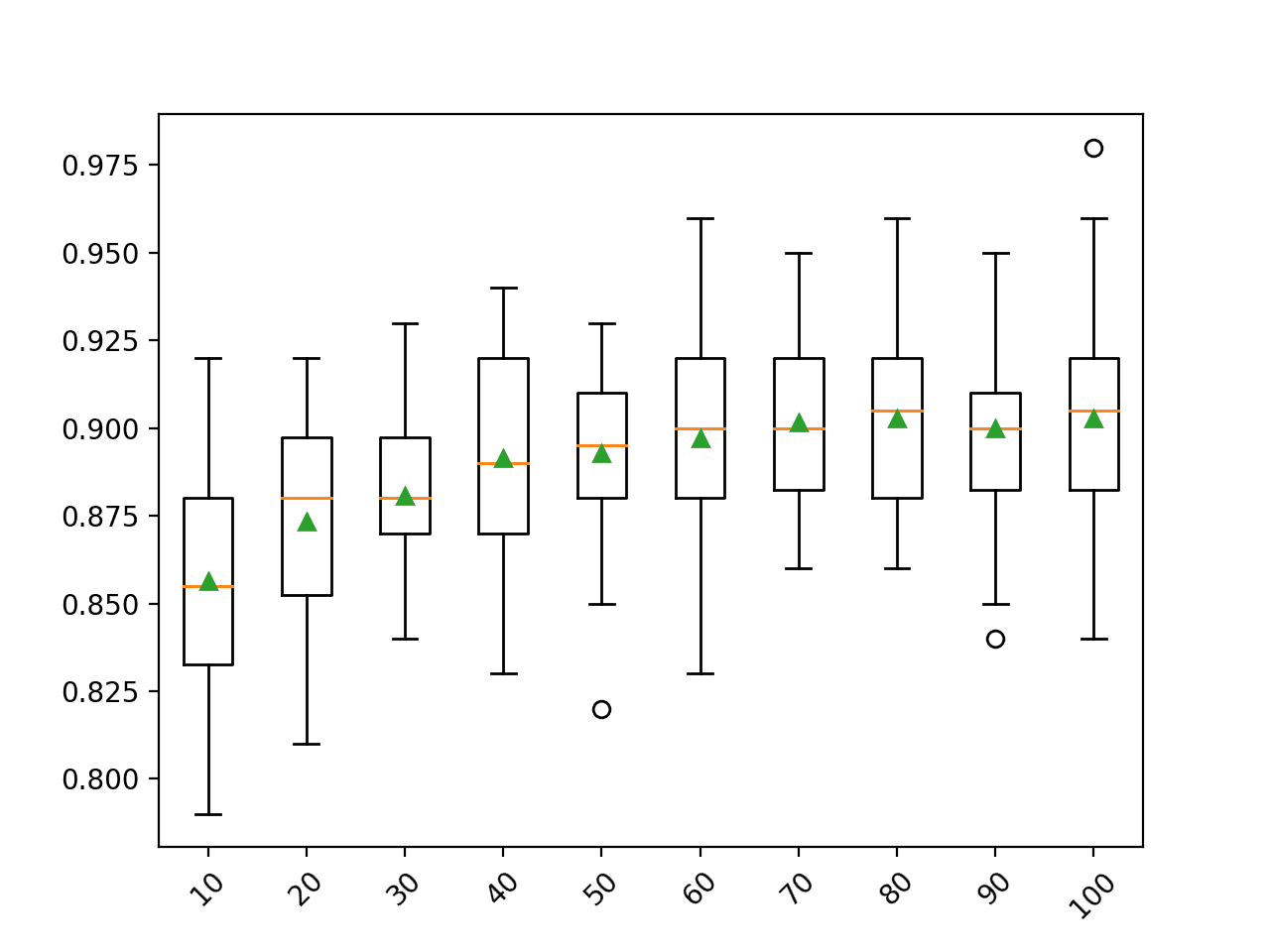
随机森林引导样本量与分类准确率的箱线图
探索特征数量
为每个分裂点随机采样的特征数量可能是配置随机森林最重要的特征。
它通过 max_features 参数设置,默认为输入特征数量的平方根。在这种情况下,对于我们的测试数据集,这将是 sqrt(20) 或大约四个特征。
下面的例子探讨了在每个分割点随机选择的特征数量对模型准确性的影响。我们将尝试从1到7的值,并期望根据启发式方法,一个较小的值(大约4)能表现良好。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 |
# 探索随机森林特征数量对性能的影响 from numpy import mean from numpy import std from sklearn.datasets import make_classification from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.ensemble import RandomForestClassifier from matplotlib import pyplot # 获取数据集 定义 获取_数据集(): X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=3) 返回 X, y # 获取要评估的模型列表 定义 获取_模型(): models = dict() # 探索从1到7的特征数量 for i in range(1,8): models[str(i)] = RandomForestClassifier(max_features=i) 返回 模型 # 使用交叉验证评估给定模型 def evaluate_model(model, X, y): # 定义评估过程 cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) # 评估模型并收集结果 scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1) 返回 分数 # 定义数据集 X, y = get_dataset() # 获取要评估的模型 模型 = 获取_模型() # 评估模型并存储结果 results, names = list(), list() for name, model in models.items(): # 评估模型 scores = evaluate_model(model, X, y) # 存储结果 results.append(scores) names.append(name) # 沿途总结性能 print('>%s %.3f (%.3f)' % (name, mean(scores), std(scores))) # 绘制模型性能以供比较 pyplot.boxplot(results, labels=names, showmeans=True) pyplot.show() |
运行示例首先报告了每个特征集数量的平均准确率。
注意:您的结果可能会有所不同,因为算法或评估过程的随机性,或数值精度上的差异。请考虑多次运行示例并比较平均结果。
在这种情况下,结果表明3到5之间的值是合适的,这证实了在此数据集上将4作为合理默认值是正确的。考虑到分类准确度的标准差比3或4更小,5的值甚至可能更好。
|
1 2 3 4 5 6 7 |
>1 0.897 (0.023) >2 0.900 (0.028) >3 0.903 (0.027) >4 0.903 (0.022) >5 0.903 (0.019) >6 0.898 (0.025) >7 0.900 (0.024) |
为每个特征集数量的准确率分数分布创建了箱线图。
我们可以看到性能的趋势是上升并在3到5之间达到峰值,然后随着特征集大小的增加而再次下降。
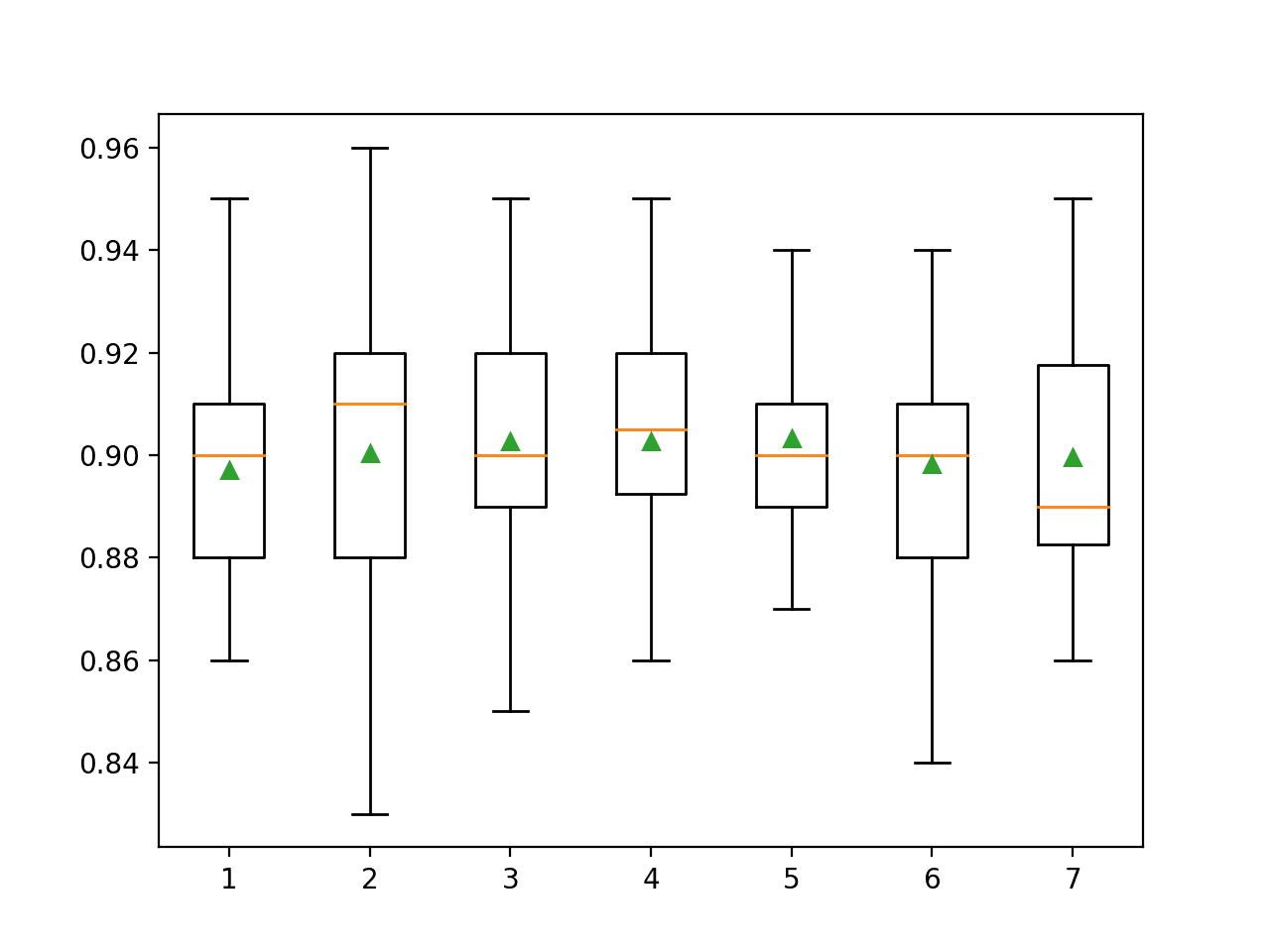
随机森林特征集大小与分类准确度的箱线图
探索树的数量
树的数量是配置随机森林的另一个关键超参数。
通常,树的数量会增加,直到模型性能稳定。直觉可能会认为更多的树会导致过拟合,但事实并非如此。由于学习算法的随机性,装袋和随机森林算法似乎对训练数据集的过拟合具有一定的免疫力。
树的数量可以通过“n_estimators”参数设置,默认为 100。
下面的例子探讨了树的数量(从10到1000)对模型性能的影响。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 |
# 探索随机森林树的数量对性能的影响 from numpy import mean from numpy import std from sklearn.datasets import make_classification from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.ensemble import RandomForestClassifier from matplotlib import pyplot # 获取数据集 定义 获取_数据集(): X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=3) 返回 X, y # 获取要评估的模型列表 定义 获取_模型(): models = dict() # 定义要考虑的树的数量 n_trees = [10, 50, 100, 500, 1000] for n in n_trees: models[str(n)] = RandomForestClassifier(n_estimators=n) 返回 模型 # 使用交叉验证评估给定模型 def evaluate_model(model, X, y): # 定义评估过程 cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) # 评估模型并收集结果 scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1) 返回 分数 # 定义数据集 X, y = get_dataset() # 获取要评估的模型 模型 = 获取_模型() # 评估模型并存储结果 results, names = list(), list() for name, model in models.items(): # 评估模型 scores = evaluate_model(model, X, y) # 存储结果 results.append(scores) names.append(name) # 沿途总结性能 print('>%s %.3f (%.3f)' % (name, mean(scores), std(scores))) # 绘制模型性能以供比较 pyplot.boxplot(results, labels=names, showmeans=True) pyplot.show() |
运行该示例首先报告每个配置的树数量的平均准确度。
注意:您的结果可能会有所不同,因为算法或评估过程的随机性,或数值精度上的差异。请考虑多次运行示例并比较平均结果。
在这种情况下,我们可以看到性能在大约100棵树后上升并保持平稳。平均准确度分数在100、500和1000棵树之间波动,这可能是统计噪声。
|
1 2 3 4 5 |
>10 0.870 (0.036) >50 0.900 (0.028) >100 0.910 (0.024) >500 0.904 (0.024) >1000 0.906 (0.023) |
为每个配置的树数量创建了准确率分数的箱线图。
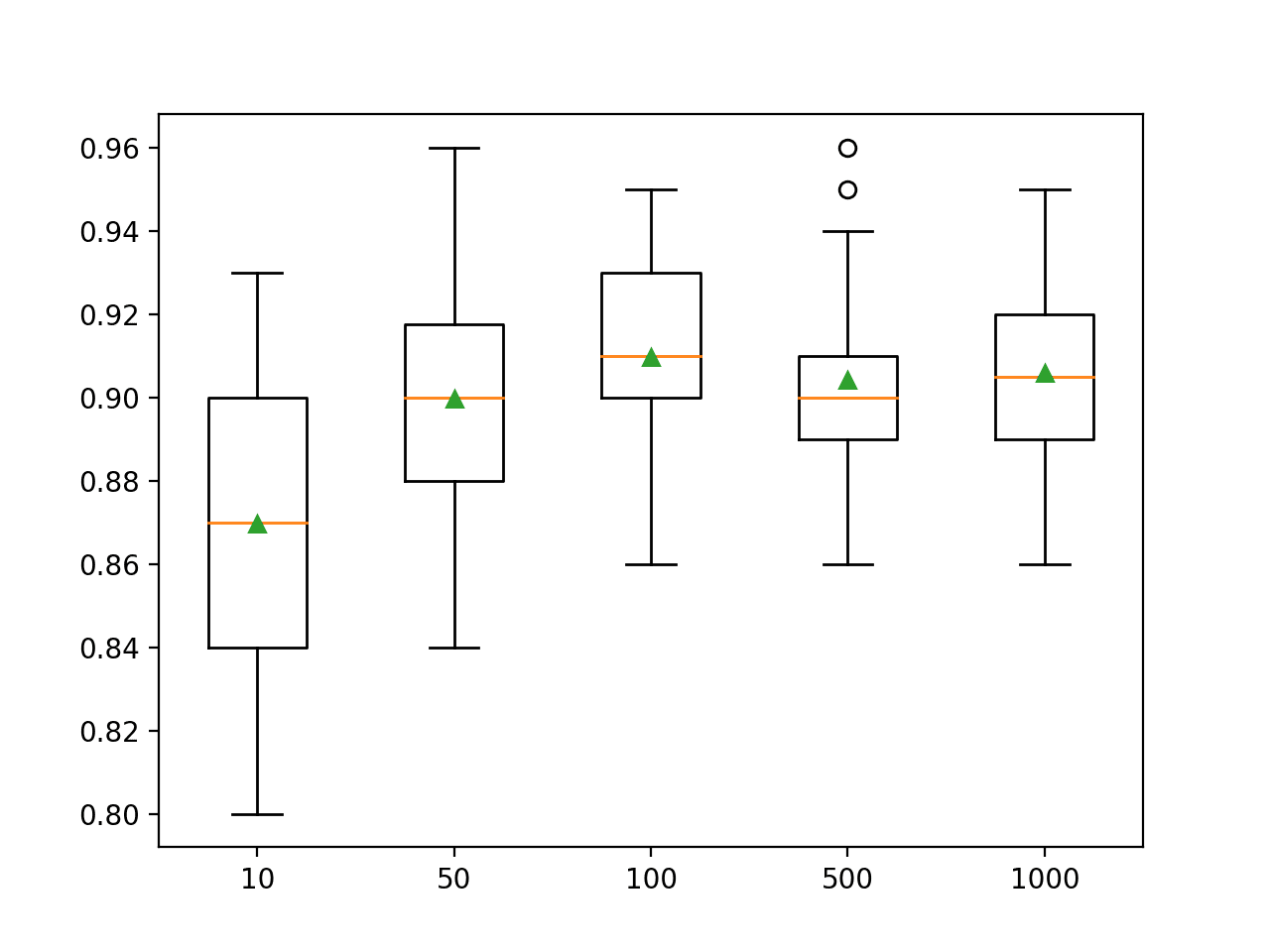
随机森林集成大小与分类准确度的箱线图
探索树深度
最后一个有趣的超参数是集成中使用的决策树的最大深度。
默认情况下,树被构建到任意深度并且不进行剪枝。这是一个合理的默认值,尽管我们也可以探索拟合具有不同固定深度的树。
最大树深度可以通过`max_depth`参数指定,默认设置为`None`(无最大深度)。
下面的例子探讨了随机森林最大树深度对模型性能的影响。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 |
# 探索随机森林树深度对性能的影响 from numpy import mean from numpy import std from sklearn.datasets import make_classification from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.ensemble import RandomForestClassifier from matplotlib import pyplot # 获取数据集 定义 获取_数据集(): X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=3) 返回 X, y # 获取要评估的模型列表 定义 获取_模型(): models = dict() # 考虑从1到7的树深度和None=完整深度 depths = [i for i in range(1,8)] + [None] for n in depths: models[str(n)] = RandomForestClassifier(max_depth=n) 返回 模型 # 使用交叉验证评估给定模型 def evaluate_model(model, X, y): # 定义评估过程 cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) # 评估模型并收集结果 scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1) 返回 分数 # 定义数据集 X, y = get_dataset() # 获取要评估的模型 模型 = 获取_模型() # 评估模型并存储结果 results, names = list(), list() for name, model in models.items(): # 评估模型 scores = evaluate_model(model, X, y) # 存储结果 results.append(scores) names.append(name) # 沿途总结性能 print('>%s %.3f (%.3f)' % (name, mean(scores), std(scores))) # 绘制模型性能以供比较 pyplot.boxplot(results, labels=names, showmeans=True) pyplot.show() |
运行该示例首先报告每个配置的最大树深度的平均准确度。
注意:您的结果可能会有所不同,因为算法或评估过程的随机性,或数值精度上的差异。请考虑多次运行示例并比较平均结果。
在这种情况下,我们可以看到更大的深度会带来更好的模型性能,并且在此数据集上,没有最大深度的默认设置实现了最佳性能。
|
1 2 3 4 5 6 7 8 |
>1 0.771 (0.040) >2 0.807 (0.037) >3 0.834 (0.034) >4 0.857 (0.030) >5 0.872 (0.025) >6 0.887 (0.024) >7 0.890 (0.025) >None 0.903 (0.027) |
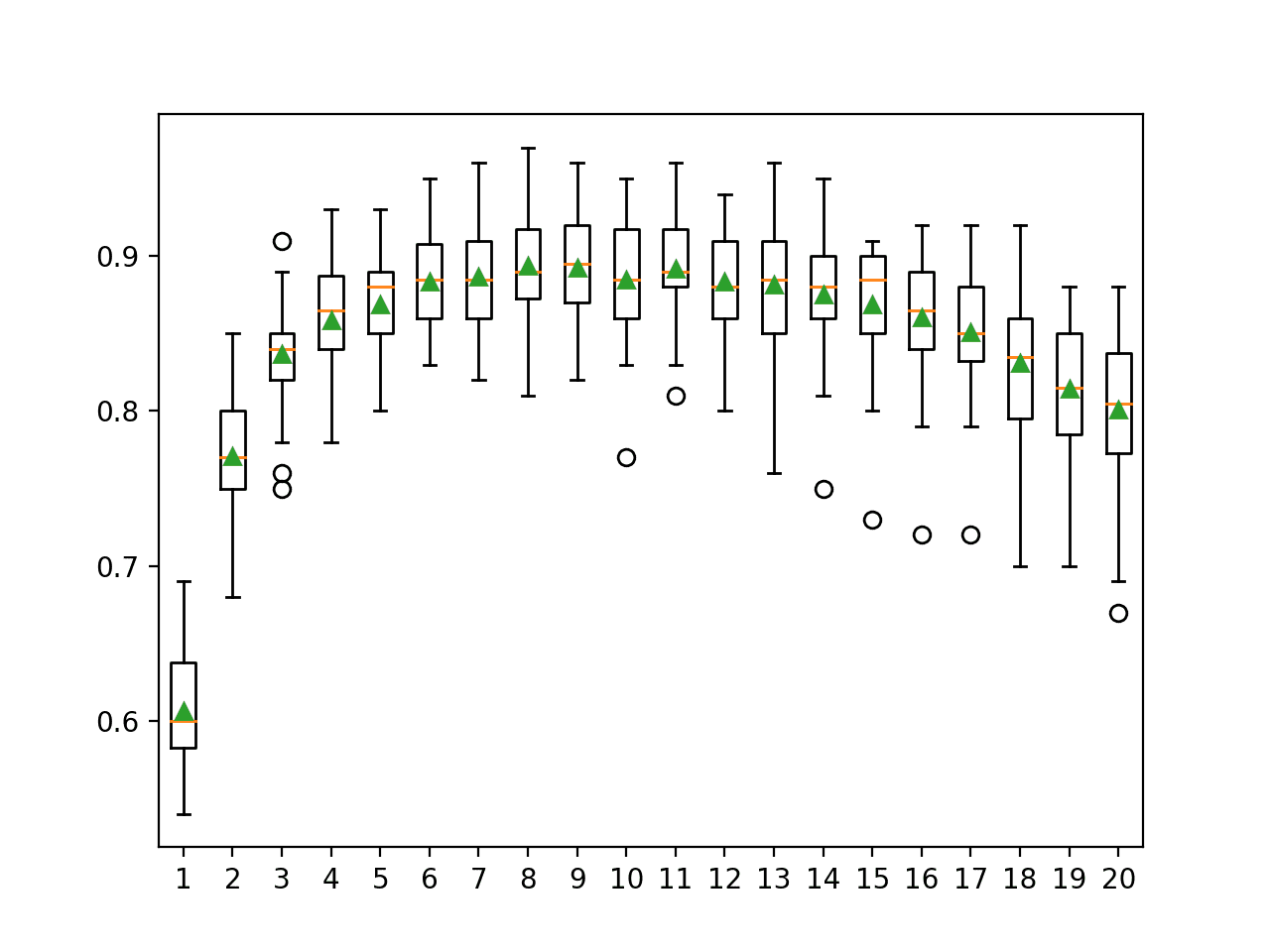
为每个配置的最大树深度创建了一个箱线图,以显示准确度分数的分布。
在这种情况下,我们可以看到性能随着树深度的增加而提高的趋势,这支持了无最大深度的默认设置。
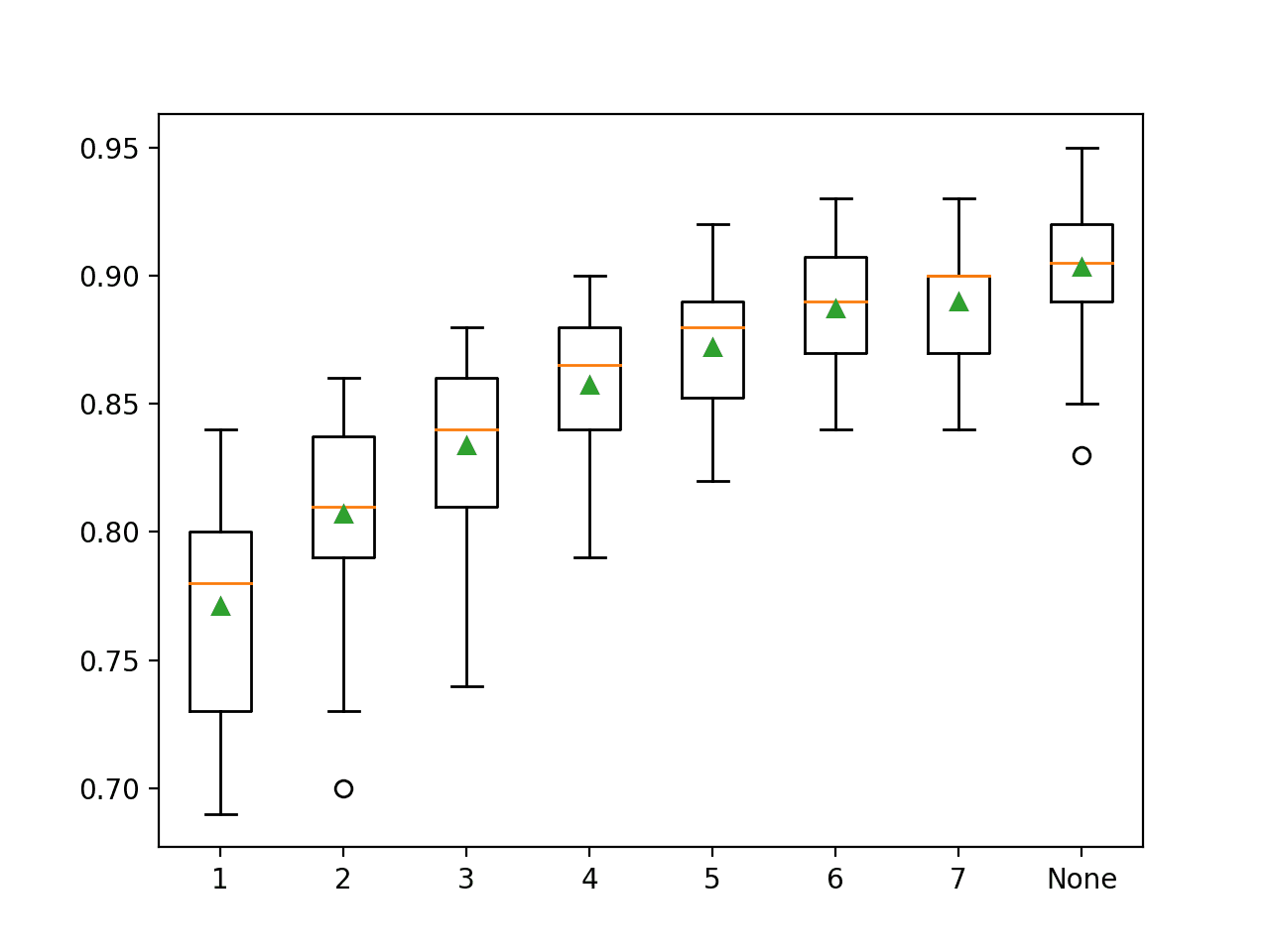
随机森林最大树深度与分类准确度的箱线图
常见问题
在本节中,我们将仔细研究一些您在使用随机森林集成过程时可能遇到的常见难点。
问:集成中应该使用什么算法?
随机森林旨在成为决策树算法的集成。
问:应该使用多少个集成成员?
树的数量应增加,直到您的数据集上性能不再有进一步的改进为止。
作为起点,我们建议至少使用1000棵树。如果交叉验证性能曲线在1000棵树时仍在改进,则继续增加树的数量,直到性能趋于平稳。
——《应用预测建模》,2013年,第200页,Applied Predictive Modeling
问:集成树太多会不会过拟合?
不。随机森林集成(不会)一般不太可能过拟合。
另一个说法是随机森林“不能过拟合”数据。增加[树的数量]确实不会导致随机森林序列过拟合…
——《统计学习基础》,2016年,第596页,The Elements of Statistical Learning
问:自助样本应该有多大?
最佳实践是使自助样本的大小与原始数据集大小相同。
即100%的大小或与原始数据集行数相同。
问:每个分割点应该选择多少个特征?
最佳实践是测试一系列不同的值,并找出最适合您的数据集的值。
作为启发式方法,您可以使用:
- 分类:特征数量的平方根。
- 回归:特征数量的三分之一。
问:哪些问题非常适合随机森林?
随机森林已知在各种分类和回归问题上表现良好甚至最佳。尝试一下就知道了。
作者对随机森林的成功做出了宏大的断言:“最准确”、“最易解释”等等。根据我们的经验,随机森林表现非常出色,只需很少的调优。
——《统计学习基础》,2016年,第590页,The Elements of Statistical Learning
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
教程
论文
- 随机森林, 2001.
书籍
- 应用预测建模, 2013.
- 统计学习基础, 2016.
- 统计学习导论:R语言应用, 2014.
API
文章
总结
在本教程中,您了解了如何开发用于分类和回归的随机森林集成。
具体来说,你学到了:
- 随机森林集成是决策树的集成,也是装袋(bagging)的自然延伸。
- 如何使用 scikit-learn 进行分类和回归的随机森林集成。
- 如何探究随机森林模型超参数对模型性能的影响。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。





嗨 Jason
希望您在这封锁期间一切安好。
一如既往的精彩文章。虽然我喜欢将RF应用于我的回归问题。然而,由于数据量巨大,我遇到了内存问题。
对于大型数据集使用RF有什么建议吗?
谢谢
丹尼斯
也许可以先在一个小样本数据上准备一个原型,看看它是否有效。
更多想法在这里
https://machinelearning.org.cn/faq/single-faq/how-can-i-run-large-models-or-models-on-lots-of-data
嗨,Jason,您是否计划出版一本关于集成的书?
目前还不确定。
您希望我写哪些集成主题?
可能是高级堆叠以及如何赢得Kaggle/数据科学竞赛
这会有帮助
https://machinelearning.org.cn/stacking-ensemble-machine-learning-with-python/
还有这个。
https://machinelearning.org.cn/super-learner-ensemble-in-python/
非常感谢您的鼎力支持!
不客气。
嗨,Jason,
我正在实现一个随机森林,我在预测中得到了一个时间序列的偏移。如果我建立模型来预测,例如,提前4步,我的预测时间序列似乎比我的观测时间序列向右偏移了4步。如果我尝试预测提前16步,它似乎偏移了16步。
有什么想法为什么会发生这种情况吗?
感谢您的所有教程!
是的,听起来模型已经学会了持久性(无技能)预测。例如,它将输入预测为输出。
嗨,Jason,
非常感谢您的回复。
我还在想,如果我尝试建立一个模型,我的训练集比我的测试集有更多的变量,我应该怎么做?
据我所知,我应该在我的测试数据框中重新创建那些缺失的变量并将它们设置为0。
训练集和测试集中的变量(列)数量必须相同。
非常棒的RF使用教程!
了解这些模型的良好实践确实很实用——根据我的经验,随机森林在实际工业应用中非常有竞争力!(通常优于人工神经网络等竞争对手)。
此致!
谢谢!
同意。XGBoost更是如此。
嗨,Jason,
请检查一下
“这意味着负MAE越大越好,一个完美的模型MAE为0。”
谢谢!非常喜欢这些内容。
这是正确的。
-10大于-100。
0大于-10。
你好Jason,我有一个问题。
我遇到了以下情况,已经用逻辑回归编程了,我尝试用随机森林来检查它如何提高准确性。
实际上,准确性提高了,但我不知道在我的问题案例中使用随机森林是否合乎逻辑。
我的案例研究如下:
基于市场数据集,我需要根据客户之前的历史预测客户是否会购买产品。即了解客户之前购买同款产品的数量,以及只是查看但未购买的数量。
使用的数据结构如下:
客户ID 当前产品 P1+ P1- P2+ P2- P3+ P3- … PN+ PN- 输出
10 CL1 P1, P3 6 1 0 0 8 2 0 0 1
11 CL1 P1, P2 7 1 5 2 0 0 0 0 1
用
CurrentProd:表示我需要知道客户是否会购买的产品列表,
P1+:表示客户购买产品1的次数,
P1-:表示客户查看产品1但未购买的次数。
列表示市场中存在的所有产品,因此我的数据有太多特征(至少200个产品),并且每行中大多数行的值为0(因为它们不属于CurrentProd)。
所以我想知道随机森林在这种情况下是否可以使用。
PS:我必须按原样使用数据,不能更改特征或结构。
客户ID..|..客户..|..当前产品..|.P1+.|.P1-.|.P2+.|.P2-.|.P3+.|.P3-.|. … .|.PN+.|.PN-.|.输出
10.|….CL1….|……P1, P3……|…6….|..1…|…0….|…0…|..8….|…2…|. … .|…0…|…0….|….1
11.|….CL1….|……P1, P2……|…7….|..1…|…5….|…2…|…0…|…0…|. … .|…0…|…0….|….1
或许可以试试并比较结果。
关键在于为问题找到合适的表示方法。这可能会给你一些想法(用产品替换网站)。
https://machinelearning.org.cn/faq/single-faq/how-to-develop-forecast-models-for-multiple-sites
感谢您的快速回复。
我已经尝试过了,它给了我一个好的结果。
但我想知道,用200个特征(产品1,产品2……)使用它是否合理。
使用能带来最佳性能的特征,无论数量多少。
如何决定这些参数
n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=3
对此有什么建议吗?
这定义了测试问题,它完全是任意的。
我的意思是,您将用您自己的数据集替换这个。
什么是最佳实践,如果我想了解这些参数的含义。
请分享一些关于超参数调优的信息。
测试问题的最佳实践?我不明白。
超参数调优的最佳实践在上述示例中,例如网格搜索。
完美!
谢谢!
感谢您如此全面的文章,
我想知道是否有办法找出我的模型在何种情况下会做出错误的预测,我的意思是,有没有办法找到(范围)特征值来告诉我学习模型的预测不可靠。或者让机器学习何时预测不可靠。
我认为这可能与机器学习的原理相反,不是吗?
有什么建议吗?
这几乎不可能知道,因为机器学习模型是从提供的数据中学习的。你只是在问提供的数据没有涵盖什么。
你好 Jason,
感谢您的文章,它们非常有用!
您知道如何获取训练模型中树的图形表示吗?我尝试在sklearn中使用`export_graphviz`,但是使用`cross_val_scores`函数独立拟合估计器,我不知道如何使用`export_graphviz`函数。
提前感谢您的回答。
Francisco
我相信这是可能的,但我之前没有做过,抱歉Francisco。
嗨,Jason,
感谢您清晰而有用的介绍。
我有一个关于随机森林算法如何处理缺失特征的问题。
例如,假设数据集是一个24小时时间序列,我想为其构建一个分类器。
有些特征只在白天可用,有些只在夜间可用,还有一些其他特征部分不可用。
如何最好地调整算法以解决此任务。
提前感谢,
伊兰
也许可以尝试一系列处理缺失数据的方法,并发现哪种方法对您的数据集最有效或最好。
非常感谢这篇文章。
我刚刚构建了自己的RF回归器,我有(2437,45)形状的数据。我运行了模型并得到了大约0.7的R平方。
我想将其提高到0.95。有什么建议吗?
感谢您的帮助!
也许这些想法中的一些会有帮助。
https://machinelearning.org.cn/machine-learning-performance-improvement-cheat-sheet/
你好,先生。
我有两个独立的数据框。一个用于训练,另一个用于测试。我需要执行随机森林分类。如何在不拆分的情况下将这些文件加载到随机森林中。
您只需先加载训练文件并分配给X_train、y_train;然后加载测试文件到X_test、y_test。但是,您必须确保格式相同,包括整数与浮点数据类型。
嗨,Jason,
我一直关注您的帖子。我有一个问题,如何在Python中将RepeatedStratifiedKFold用于随机森林回归?您有相关的教程吗?谢谢!
您认为这里的例子有效吗?https://machinelearning.org.cn/dynamic-ensemble-selection-in-python/
嗨,Json,
感谢您又一篇有用的帖子。在博客中,您提到不建议关闭自助法(bootstrap)。
“如果您愿意,可以通过将‘bootstrap’参数设置为False来关闭它。在这种情况下,整个训练数据集将用于训练每个决策树。不建议这样做。”
如果我的X和y本质上是时间相关的呢?例如,它们来自物联网传感器(例如,气象观测)。关闭自助法以保留时间结构是有意义的,对吗?
有什么建议/推荐吗?
谢谢
对于RFR,当使用CV时,它会告诉我们准确度平均值,一切都很好,但是……如果我们说,好的,我想用它来预测……我该怎么做呢?因为我还没有进行fit()。在这篇文档中,fit()部分是作为CV的“替代”完成的,预测是使用这个拟合的模型进行的……但是如果我想使用一个用CV拟合的模型呢?我该怎么做?
嗨,Pedro……您可能会对以下内容感兴趣
https://towardsdatascience.com/random-forest-ca80e56224c1
嗨!我想知道,如果将重复k折交叉验证应用于预测分类特征(地图),是否真的需要测试集?
此致!
你好Dim……以下内容可能有助于澄清K折交叉验证的概念
https://machinelearning.org.cn/k-fold-cross-validation/
你好。
感谢您这篇详细的关于使用随机森林算法的文章和演示。
我对自助样本大小有一个疑问。
先生,您提到将样本大小设置为完整的训练数据集会使决策树更相似,而较小的样本大小会使它们更不同。但根据图表,准确性似乎随着样本大小超参数的增加而增加。这怎么可能呢?因为这难道不意味着决策树模型相对更相关,因为它们是在相同的完整数据集上训练的吗?如果是这样,实际问题应该使用多大百分比的自助样本大小才是正确的?
提前感谢。
嗨,PriyaKS……以下资源提供了对自助法的一个很好的介绍。
https://machinelearning.org.cn/a-gentle-introduction-to-the-bootstrap-method/
感谢您关于自助法的精彩文章。它澄清了采样过程背后究竟发生了什么。但是,我仍然无法将“较小的样本量会使树更不同,而较大的样本量会使树更相似”这一说法与较大的样本量(相似的树)带来更好的准确性联系起来。我们是否需要树更不同或更相似才能获得更高的准确性?——因为,在讨论特征数量时,理由是“通过将特征减少到在每个分裂点可能考虑的随机子集,它迫使集成中的每个决策树变得更不同”。
所以,如果能进一步澄清为什么较大的样本量(相似的树)会带来更好的准确性,我将不胜感激,先生。
先谢谢您了。
非常感谢您的精彩文章!我从中学到了很多。
一个小提示:我猜下面的句子可能有一个错别字:“A bootstrap sample is a sample of the training dataset where a sample may appear more than once in the sample, referred to as sampling with replacement.”
这个版本怎么样?:“A bootstrap sample is a sample of the training dataset where AN OBSERVATION may appear more than once in the sample, referred to as sampling with replacement.”
谢谢!请继续发帖🙂
嗨 Oz……您的版本确实更清晰、更准确。这是您建议修改后的句子。
“自助样本是训练数据集的一个样本,其中一个观测值可以在样本中出现多次,这被称为有放回抽样。”
这准确地表达了个别观测值(数据点)可以在自助样本中重复出现,这是有放回抽样的本质。