在神经网络中,激活函数负责将节点加权输入的总和转换为节点的激活值或该输入的输出。
ReLU(Rectified Linear Unit),简称为ReLU,是一种分段线性函数,当输入为正时,直接输出输入值;否则,输出零。它已成为许多类型神经网络的默认激活函数,因为使用它的模型更容易训练,并且通常能获得更好的性能。
在本教程中,您将了解用于深度学习神经网络的ReLU激活函数。
完成本教程后,您将了解:
- 由于梯度消失问题,Sigmoid和双曲正切激活函数无法用于具有许多层的网络。
- ReLU激活函数解决了梯度消失问题,使模型能够更快地学习并获得更好的性能。
- 在开发多层感知机和卷积神经网络时,ReLU激活函数是默认的。
用我的新书《更好的深度学习》来启动你的项目,书中包含分步教程和所有示例的 Python 源代码文件。
让我们开始吧。
- 2019年6月:修正了He权重初始化公式中的错误(感谢Maltev)。

ReLU激活函数在深度学习神经网络中的入门介绍
照片由美国土地管理局拍摄,部分权利保留。
教程概述
本教程分为六个部分;它们是:
- Sigmoid和Tanh激活函数的局限性
- ReLU激活函数
- 如何实现ReLU激活函数
- ReLU激活函数的优点
- 使用ReLU的技巧
- ReLU的扩展和替代方案
Sigmoid和Tanh激活函数的局限性
神经网络由节点层组成,并学习将输入示例映射到输出。
对于给定节点,输入乘以节点中的权重并求和。此值称为节点的加权激活。然后,加权激活通过激活函数进行转换,从而定义节点的特定输出或“激活”。
最简单的激活函数称为线性激活,根本不进行任何转换。仅由线性激活函数组成的网络易于训练,但无法学习复杂的映射函数。在线性模型中,预测量(例如回归问题)的输出层仍然使用线性激活函数。
非线性激活函数更受欢迎,因为它们允许节点学习数据中更复杂的结构。传统上,两个广泛使用的非线性激活函数是Sigmoid和双曲正切激活函数。
Sigmoid激活函数,也称为Logistic函数,传统上是神经网络中非常流行的激活函数。函数输入被转换为0.0到1.0之间的值。大于1.0的输入被转换为1.0,类似地,小于0.0的值被“压缩”到0.0。函数对于所有可能输入的形状是从零到0.5再到1.0的S形。在很长一段时间里,直到20世纪90年代初,它一直是神经网络默认使用的激活函数。
双曲正切函数,简称tanh,是一个形状相似的非线性激活函数,其输出值在-1.0和1.0之间。在20世纪90年代后期和21世纪初,tanh函数比Sigmoid激活函数更受欢迎,因为使用它的模型更容易训练,并且通常具有更好的预测性能。
……双曲正切激活函数通常比Logistic Sigmoid表现更好。
— 第195页,《深度学习》,2016年。
Sigmoid和tanh函数的一个普遍问题是它们会饱和。这意味着大值会被压缩到1.0,而小值会被压缩到tanh和sigmoid各自的-1或0。此外,这些函数仅在输入的中点附近(例如sigmoid的0.5和tanh的0.0)才真正对变化敏感。
无论节点提供的加权激活输入是否包含有用信息,函数的有限敏感性和饱和度都会发生。一旦饱和,学习算法就很难继续调整权重来提高模型的性能。
……Sigmoid单元在其大部分定义域内都会饱和——当z非常正时它们饱和到高值,当z非常负时它们饱和到低值,并且仅当z接近0时它们对输入才敏感。
— 第195页,《深度学习》,2016年。
最后,随着硬件能力的提高,通过GPU使用深度神经网络,使用Sigmoid和tanh激活函数很难进行训练。
在大型网络中,具有这些非线性激活函数的深层层无法接收到有用的梯度信息。误差通过网络反向传播并用于更新权重。给定所选激活函数的导数,误差量随着反向传播的每一层而急剧减少。这被称为梯度消失问题,它阻碍了深度(多层)网络有效地学习。
梯度消失使得很难知道参数应该向哪个方向移动以改进成本函数。
— 第290页,《深度学习》,2016年。
有关ReLU如何解决梯度消失问题的示例,请参阅教程
尽管使用非线性激活函数允许神经网络学习复杂的映射函数,但它们有效地阻止了学习算法与深度网络协同工作。
在2000年代末和2010年代初,通过使用替代网络类型,例如Boltzmann机和逐层训练或无监督预训练,找到了解决方法。
想要通过深度学习获得更好的结果吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
ReLU激活函数
为了使用随机梯度下降与误差反向传播来训练深度神经网络,需要一种激活函数,该函数看起来和行为都像线性函数,但实际上是非线性函数,允许学习数据中的复杂关系。
该函数还必须对加权激活输入提供更多的敏感性,并避免容易饱和。
这个解决方案在该领域已经存在了一段时间,尽管直到2009年和2011年的论文才引起人们的关注。
解决方案是使用ReLU(Rectified Linear Unit)激活函数,简称ReLU。
实现此激活函数的节点或单元称为ReLU激活单元,简称ReLU。通常,使用ReLU函数作为隐藏层激活函数的网络被称为ReLU网络。
ReLU的应用很容易被认为是深度学习革命的里程碑之一,例如,它使得常规开发非常深的神经网络成为可能的技术。
[另一个]主要的算法变革极大地提高了前馈网络的性能,就是用分段线性隐藏单元(如ReLU)替换Sigmoid隐藏单元。
— 第226页,《深度学习》,2016年。
ReLU激活函数是一个简单的计算,它直接返回输入的数值,或者如果输入为0.0或更小,则返回0.0。
我们可以用一个简单的if语句来描述这个函数:
|
1 2 3 4 |
if input > 0 return input else return 0 |
我们可以用max()函数来数学上描述这个函数g(),它计算0.0和输入z集合中的最大值;例如:
|
1 |
g(z) = max{0, z} |
该函数对于大于零的值是线性的,这意味着它具有线性激活函数的许多理想特性,当使用反向传播训练神经网络时。然而,它是一个非线性函数,因为负值总是输出为零。
由于ReLU单元接近线性,它们保留了许多使线性模型易于通过基于梯度的方法进行优化的属性。它们也保留了许多使线性模型泛化良好的属性。
— 第175页,《深度学习》,2016年。
由于ReLU函数在一半输入域上是线性的,另一半是非线性的,因此它被称为分段线性函数或铰链函数。
然而,该函数在某种意义上仍然非常接近线性,因为它是一个具有两个线性部分的分段线性函数。
— 第175页,《深度学习》,2016年。
现在我们熟悉了ReLU激活函数,让我们看看如何在Python中实现它。
如何编写ReLU激活函数
我们可以在Python中轻松实现ReLU激活函数。
也许最简单的实现就是使用max()函数;例如:
|
1 2 3 |
# ReLU函数 def rectified(x): return max(0.0, x) |
我们期望任何正值都会被原样返回,而输入值为0.0或负值将被返回为0.0。
以下是一些ReLU激活函数的输入和输出示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# 演示ReLU函数 # ReLU函数 def rectified(x): return max(0.0, x) # 用正输入演示 x = 1.0 print('rectified(%.1f) is %.1f' % (x, rectified(x))) x = 1000.0 print('rectified(%.1f) is %.1f' % (x, rectified(x))) # 用零输入演示 x = 0.0 print('rectified(%.1f) is %.1f' % (x, rectified(x))) # 用负输入演示 x = -1.0 print('rectified(%.1f) is %.1f' % (x, rectified(x))) x = -1000.0 print('rectified(%.1f) is %.1f' % (x, rectified(x))) |
运行示例,我们可以看到正值无论大小都会被返回,而负值则被压缩到0.0。
|
1 2 3 4 5 |
rectified(1.0) is 1.0 rectified(1000.0) is 1000.0 rectified(0.0) is 0.0 rectified(-1.0) is 0.0 rectified(-1000.0) is 0.0 |
通过绘制一系列输入和计算出的输出来了解函数输入与输出之间的关系。
下面的示例生成从-10到10的整数系列,计算每个输入的ReLU激活值,然后绘制结果。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# 绘制输入和输出 from matplotlib import pyplot # ReLU函数 def rectified(x): return max(0.0, x) # 定义一系列输入 series_in = [x for x in range(-10, 11)] # 计算我们输入的输出 series_out = [rectified(x) for x in series_in] # 输入到ReLU输出的折线图 pyplot.plot(series_in, series_out) pyplot.show() |
运行示例会生成一个折线图,显示所有负值和零输入都被压缩到0.0,而正输出则按原样返回,从而产生一个线性增长的斜率,因为我们创建了一个线性增长的正值系列(例如1到10)。
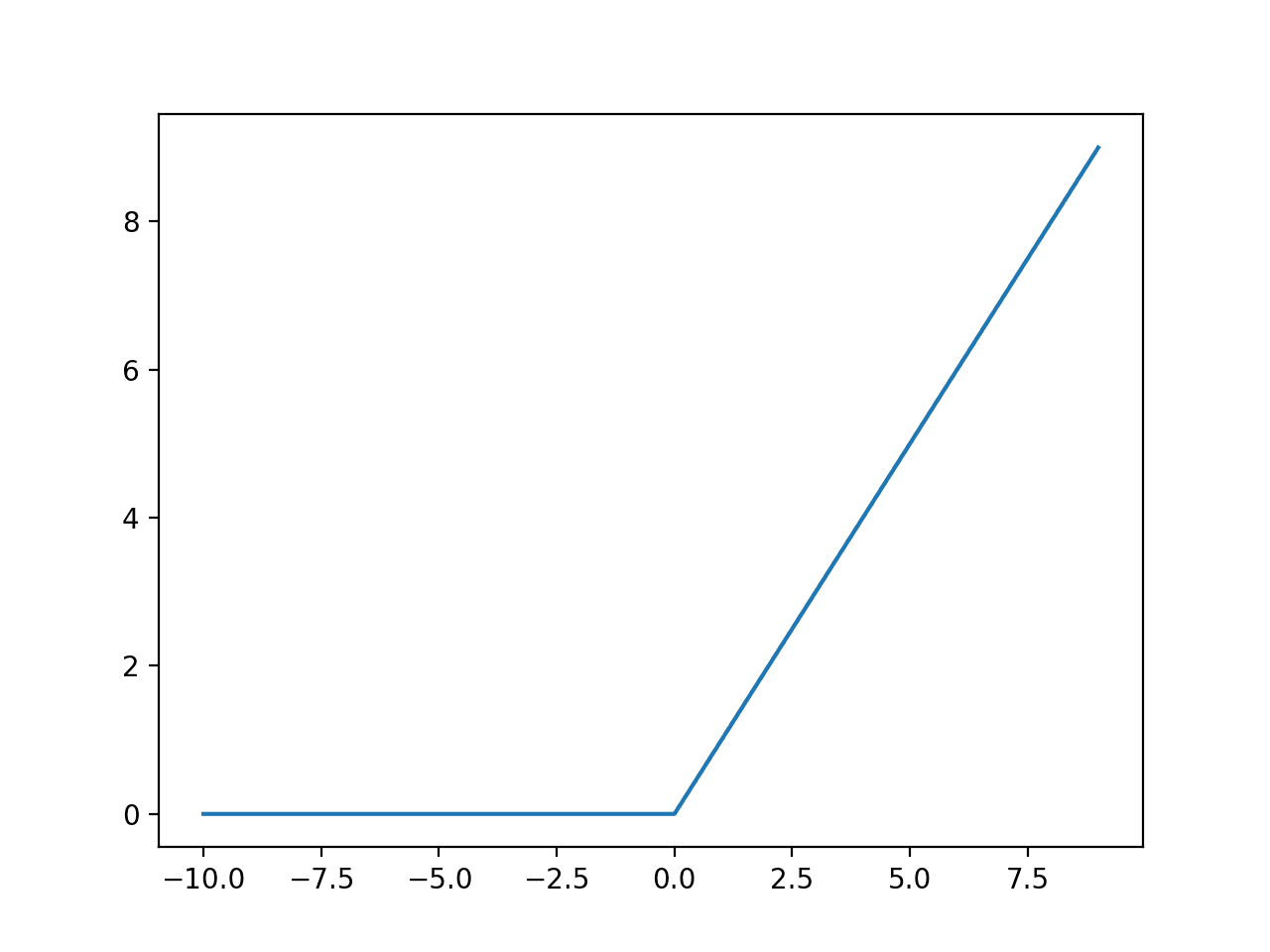
负值和正值ReLU激活的折线图
ReLU函数的导数也容易计算。请记住,在反向传播误差以更新节点权重时,需要激活函数的导数。
函数的导数就是斜率。负值的斜率为0.0,正值的斜率为1.0。
传统上,神经网络领域一直避免使用任何不是完全可微的激活函数,这可能延迟了ReLU和其他分段线性函数的采用。严格来说,我们无法计算输入为0.0时的导数,因此我们可以假设它为零。这在实践中不是问题。
例如,ReLU函数 g(z) = max{0, z} 在 z = 0 处不可微。这似乎使g对于基于梯度学习算法的使用无效。在实践中,梯度下降仍然表现得足够好,使得这些模型可以用于机器学习任务。
— 第192页,《深度学习》,2016年。
使用ReLU激活函数有许多优点;让我们在下一节中看一些。
ReLU激活函数的优点
ReLU激活函数已迅速成为开发大多数类型神经网络时的默认激活函数。
因此,花点时间回顾一下该方法的一些好处很重要,这些好处首先由Xavier Glorot等人在于2012年发表的关于使用ReLU的里程碑式论文“Deep Sparse Rectifier Neural Networks”中提出。
1. 计算简单。
ReLU函数实现起来非常简单,只需要一个max()函数。
这与需要指数计算的tanh和Sigmoid激活函数不同。
计算也更便宜:激活中不需要计算指数函数
— 《Deep Sparse Rectifier Neural Networks》,2011年。
2. 表示稀疏性
ReLU函数的一个重要优点是它能够输出一个真实的零值。
这与tanh和Sigmoid激活函数不同,它们学习近似零输出,例如一个非常接近零但不是真实零的值。
这意味着负输入可以输出真实的零值,允许神经网络隐藏层的激活包含一个或多个真实的零值。这被称为稀疏表示,并且是表示学习中的一个理想属性,因为它可以加速学习和简化模型。
在自动编码器中,高效表示(如稀疏性)被研究和寻求,其中网络学习输入的紧凑表示(称为代码层),例如图像或序列,然后在从紧凑表示中重构之前。
对于稀疏(和去噪)自动编码器实现实际零值的一种方法 […] 想法是使用ReLU来生成代码层。通过一个实际上将表示推向零的先验(如绝对值惩罚),人们可以间接控制表示中零的平均数量。
— 第507页,《深度学习》,2016年。
3. 线性行为
ReLU函数在大多数情况下看起来和行为都像一个线性激活函数。
总的来说,一个神经网络更容易优化,当它的行为是线性的或接近线性的时候。
ReLU单元……基于模型如果其行为更接近线性则更容易优化的原理。
— 第194页,《深度学习》,2016年。
这一属性的关键在于,使用此激活函数训练的网络几乎完全避免了梯度消失问题,因为梯度保持与节点激活成比例。
由于这种线性,梯度在神经元的激活路径上良好流动(由于Sigmoid或Tanh单元的激活非线性,没有梯度消失效应)。
— 《Deep Sparse Rectifier Neural Networks》,2011年。
4. 训练深度网络
重要的是,ReLU激活函数的(重新)发现和采用意味着利用硬件改进并成功使用反向传播训练具有非线性激活函数的深度多层网络成为可能。
反过来,像Boltzmann机这样的复杂网络以及逐层训练和无标签预训练这样的复杂训练方案都可以被抛弃。
……深度ReLU网络可以在不进行任何无监督预训练的情况下,在纯粹监督任务和大型标记数据集上达到最佳性能。因此,这些结果可以被视为理解训练深度但纯粹监督神经网络的困难,并缩小有监督和无监督预训练神经网络之间性能差距的新里程碑。
— 《Deep Sparse Rectifier Neural Networks》,2011年。
使用ReLU的技巧
在本节中,我们将介绍一些在自己的深度学习神经网络中使用ReLU的技巧。
将ReLU用作默认激活函数
长期以来,默认激活函数是Sigmoid激活函数。后来是tanh激活函数。
对于现代深度学习神经网络,默认激活函数是ReLU激活函数。
在引入ReLU单元之前,大多数神经网络使用Logistic Sigmoid激活函数或双曲正切激活函数。
— 第195页,《深度学习》,2016年。
大多数取得最先进成果的论文都会描述使用ReLU的网络。例如,在Alex Krizhevsky等人在2012年发表的里程碑式论文《ImageNet Classification with Deep Convolutional Neural Networks》中,作者开发了一个具有ReLU激活的深度卷积神经网络,在ImageNet照片分类数据集上取得了最先进的成果。
……我们将具有此非线性的神经元称为ReLU(Rectified Linear Units)。具有ReLU的深度卷积神经网络比具有Tanh单元的等效网络训练速度快几倍。
如果不确定,请在神经网络中从ReLU开始,然后尝试其他分段线性激活函数,看看它们的性能如何。
在现代神经网络中,默认建议是使用ReLU或ReLU。
— 第174页,《深度学习》,2016年。
将ReLU用于MLP、CNN,但可能不用于RNN
ReLU可以用于大多数类型的神经网络。
它被推荐为多层感知机(MLP)和卷积神经网络(CNNs)的默认选项。
ReLU与CNNs结合使用的研究已非常透彻,并且几乎普遍地(最初是令人惊讶地)带来了结果的改进。
……滤波器组之后的非线性如何影响识别精度。令人惊讶的答案是,使用校正非线性是提高识别系统性能最重要的因素。
— 《What is the best multi-stage architecture for object recognition?》,2009年。
对ReLU与CNNs结合使用的研究引发了它们与其他网络类型的结合使用。
[其他人]已经探索了各种校正非线性……在卷积网络中,并发现它们提高了判别性能。
— 《Rectified Linear Units Improve Restricted Boltzmann Machines》,2010年。
当将ReLU与CNNs结合使用时,它们可以用作滤波器图本身的激活函数,然后是池化层。
卷积网络的一个典型层由三个阶段组成……在第二阶段,每个线性激活都通过非线性激活函数,例如ReLU激活函数。此阶段有时称为检测器阶段。
— 第339页,《深度学习》,2016年。
传统上,LSTM使用tanh激活函数作为单元状态的激活,并使用Sigmoid激活函数作为节点输出。考虑到它们精心设计,人们认为ReLU默认情况下不适用于循环神经网络(RNN),如长短期记忆网络(LSTM)。
乍一看,ReLU似乎不适用于RNN,因为它们可能有非常大的输出,因此预计它们比具有有界值的单元更容易爆炸。
— 《A Simple Way to Initialize Recurrent Networks of Rectified Linear Units》,2015年。
尽管如此,一些研究工作仍在探索将ReLU用作LSTM中的输出激活,结果是仔细初始化网络权重以确保网络在训练前是稳定的。这在2015年题为“A Simple Way to Initialize Recurrent Networks of Rectified Linear Units”的论文中有概述。
尝试较小的偏置输入值
偏置是节点中具有固定值的输入。
偏置的效果是移动激活函数,传统的做法是将偏置输入值设置为1.0。
在网络中使用ReLU时,请考虑将偏置设置为一个较小的值,例如0.1。
……将[偏置]的所有元素设置为一个小的正值(例如0.1)可能是一个好习惯。这使得ReLU单元对于训练集中的大多数输入最初都很可能处于激活状态,并允许导数通过。
— 第193页,《深度学习》,2016年。
关于这是否是必需的有一些相互矛盾的报告,因此请将性能与具有1.0偏置输入的模型进行比较。
使用“He权重初始化”
在训练神经网络之前,必须将网络权重初始化为小的随机值。
在网络中使用ReLU并将权重初始化为以零为中心的微小随机值时,网络中一半的单元将输出零值。
例如,在统一初始化权重后,约50%的隐藏单元连续输出值是真实的零值。
— 《Deep Sparse Rectifier Neural Networks》,2011年。
有许多启发式方法可以初始化神经网络的权重,但没有最好的权重初始化方案,并且在一般准则之外,将权重初始化方案映射到激活函数的选择关系很小。
在ReLU被广泛采用之前,Xavier Glorot和Yoshua Bengio在他们2010年题为“Understanding the difficulty of training deep feedforward neural networks”的论文中提出了一种初始化方案,该方案很快成为使用Sigmoid和Tanh激活函数的默认方案,通常称为“Xavier初始化”。权重被设置为随机值,这些值均匀地采样于一个范围,该范围与前一层的节点数量成正比(具体来说是+/- 1/sqrt(n),其中n是前一层的节点数)。
Kaiming He等人(2015年)在他们题为“Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification”的论文中建议Xavier初始化和其他方案不适用于ReLU及其扩展。
Glorot和Bengio建议采用适当缩放的均匀分布进行初始化。这被称为“Xavier”初始化[……]。其推导基于激活是线性的假设。此假设对ReLU无效。
— 《Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification》,2015年。
他们提出对Xavier初始化进行小的修改,使其适用于ReLU,现在通常称为“He初始化”(具体为+/- sqrt(2/n),其中n是上一层称为扇入的节点数)。在实践中,可以使用高斯和均匀版本的方案。
缩放输入数据
在使用神经网络之前缩放输入数据是一个好习惯。
这可能包括将变量标准化为零均值和单位方差,或将每个值归一化到0到1的范围内。
在许多问题中,如果不进行数据缩放,神经网络的权重可能会变得很大,导致网络不稳定并增加泛化误差。
这个良好的输入缩放实践,无论在网络中使用ReLU与否都适用。
使用权重衰减
根据设计,ReLU的输出在正域是无界的。
这意味着在某些情况下,输出会持续增大。因此,使用某种形式的权重正则化可能是一个好主意,例如L1或L2范数。
由于激活的无界行为,也可能出现另一个问题;因此,人们可能希望使用正则化器来防止潜在的数值问题。因此,我们对激活值使用L1惩罚,这也促进了额外的稀疏性。
— 《Deep Sparse Rectifier Neural Networks》,2011年。
这可以是一个好习惯,既可以促进稀疏表示(例如使用L1正则化),也可以减少模型的泛化误差。
ReLU的扩展和替代方案
ReLU确实存在一些局限性。
ReLU局限性的关键在于,权重更新很大导致激活函数加权输入总和始终为负,无论网络输入如何。
这意味着带有此问题的节点将永远输出激活值为0.0。这被称为“死ReLU”。
只要单元不激活,梯度就是0。这可能导致单元永远不激活的情况,因为基于梯度的优化算法不会调整从未初始激活的单元的权重。此外,与梯度消失问题一样,我们可以预期使用恒定0梯度的ReLU网络训练时学习会很慢。
— 《Rectifier Nonlinearities Improve Neural Network Acoustic Models》,2013年。
一些流行的ReLU扩展以某种方式放宽了函数的非线性输出,允许出现小的负值。
Leaky ReLU(LReLU或LReL)修改了函数,当输入小于零时允许出现小的负值。
Leaky ReLU允许单元饱和和不激活时出现小的非零梯度。
— 《Rectifier Nonlinearities Improve Neural Network Acoustic Models》,2013年。
指数线性单元(ELU)是ReLU的泛化,它使用参数化指数函数从正值过渡到小的负值。
ELU具有负值,这使得激活的平均值更接近零。平均激活值更接近零可以加快学习速度,因为它们使梯度更接近自然梯度。
— 《Fast and Accurate Deep Network Learning by Exponential Linear Units (ELUs)》,2016年。
参数化ReLU(PReLU)学习控制函数形状和泄漏程度的参数。
……我们提出了一种新的ReLU泛化,我们称之为参数化ReLU(PReLU)。这种激活函数自适应地学习校正器的参数。
— 《Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification》,2015年。
Maxout是另一种分段线性函数,它返回输入的最大值,设计用于与dropout正则化技术结合使用。
我们定义了一个简单的名为maxout的新模型(之所以如此命名,是因为它的输出是一组输入的max值,并且它与dropout是自然的伴侣),它旨在通过dropout促进优化,并提高dropout的快速近似模型平均技术的准确性。
— 《Maxout Networks》,2013年。
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
文章
书籍
- 第6.3.1节 ReLU及其泛化,《深度学习》,2016年。
论文
- 什么是最佳的多阶段对象识别架构?, 2009
- ReLU改进了受限玻尔兹曼机, 2010.
- 深度稀疏校正器神经网络, 2011.
- 校正器非线性改进神经网络声学模型, 2013.
- 理解深度前馈神经网络训练的困难, 2010.
- 深入研究整流器:在 ImageNet 分类中超越人类水平的表现, 2015.
- Maxout 网络, 2013.
API
文章
总结
在本教程中,您了解了深度学习神经网络的整流线性激活函数。
具体来说,你学到了:
- 由于梯度消失问题,Sigmoid和双曲正切激活函数无法用于具有许多层的网络。
- ReLU激活函数解决了梯度消失问题,使模型能够更快地学习并获得更好的性能。
- 在开发多层感知机和卷积神经网络时,ReLU激活函数是默认的。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。





这是一个很棒的解释。谢谢。
谢谢,很高兴对您有帮助。
优秀的解释,并辅以额外的资源。谢谢你,Jason。
很高兴它有帮助。
我们如何分析神经网络的性能?是指均方误差最小化,并且验证、测试和训练图吻合吗?我们还可以通过哪些方式来分析其性能?
这很大程度上取决于问题的具体情况。
对于回归预测建模问题,多次运行的平均 MSE 可能是有意义的。
如果我们反过来做会怎样?我的意思是,如果我们使用 dark-ReLU min(x,0)。Dark-ReLU 将为正值输出 0。
可能是糟糕的结果,例如,我们在将加权输入传递给激活函数之前对它们进行求和。我认为这会鼓励负的加权和。尽管如此,还是试试看会发生什么。
请告诉我 ReLU 是否有助于在嘈杂环境中检测音频信号的问题。我已经购买了您所有的书籍
可能会。试试看。
很好的介绍,谢谢!
我正在上一门关于深度学习的在线课程。在课程材料介绍它之前,我读了您的帖子并实现了 He 初始化。
现在,我认为您的方程中有一个笔误,您写的是“2/sqrt(n)”,而它应该是 sqrt(2/n),对吗?
你说得对,已修正。谢谢!
很棒的文章。
谢谢,很高兴对您有帮助。
像 sigmoid 和 tanh 这样的平滑函数用于进行非线性变换,理论上可以学习任何模式。通过将相同的值传递给加权输入的正部分,我们是否会失去这种“保证”?
不。我们获得了灵活性。
ReLU 也是非线性的,因此它保持了您提到的对于 logit 或 tanh 样式函数相同的“保证”。关键在于激活函数不必是连续或有界的,以确保网络的通用性。当然,ReLU 碰巧为我们提供了几种不错的优化,可以使实际实现更容易,但整体理论保持不变。
如果你仔细想想,你最终会得到一个线性投影的开关系统。
对于特定的输入以及该输入周围的特定邻域,从输入到输出的特定线性投影是有效的。直到输入的改变足够大,以至于某些开关(ReLU)翻转状态。由于开关发生在零,因此当系统从一个线性投影更改为另一个线性投影时,输出不会出现突然的不连续性。
这是一个很好的思考方式,Sean,谢谢。
没问题。只是对于一些不理解的人来说——当开关打开时,1 伏特输入会产生 1 伏特输出,n 伏特输入会产生 n 伏特输出。当您绘制图形时,这会给您一条 45 度线。当它关闭时,您会得到零伏特输出,一条直线。
ReLU 那么就是一个带有自身决策策略的开关。
多个加权和的加权和仍然是一个线性系统。
那么 ReLU 神经网络就是一个开关系统,它由加权和的加权和……组成。
由于开关发生在零点,因此对于输入的渐变,开关期间没有不连续性。
对于特定的输入和特定的输出神经元,输出是加权和的线性组合,可以将其转换为输入的单个加权和。也许您可以看一下那个加权和,看看神经网络在输入中寻找什么。或者有一些可以计算的指标,比如输入向量和最终加权和的权重向量之间的角度。
很棒的教程,非常感谢。
一个小细节:我认为您在此处给出的解释在数学上不完全正确
“由于整流函数对于输入域的一半是线性的,对于另一半是非线性的,因此它被称为分段线性函数或铰链函数。”
实际上,整流函数在其所指的两个输入域的一半上都是线性的,但作为一个整体,它不满足线性(请参见例如 https://en.wikipedia.org/wiki/Linearity#In_mathematics)的性质,即可加性
f(x + y) = f(x) + f(y)。
(如果 x 和 y 符号不同,这显然不成立。)
和一度齐次性
f(αx) = αf(x) 对于所有 α。
(对于 α<0,这不成立。)
太好了,谢谢您指出这一点!
如何使用 SPSS 神经网络预测输出 Y?我不知道如何使用该模型进行预测。如何计算具有特定 X 值的 Y 值?
谢谢您。
抱歉,我不知道 SPSS。
感谢您如此简洁的解释。🙂已加入书签
不客气,很高兴它有所帮助!
你好,杰森,
您能告诉我 ReLU 的原始研究论文名称吗?预先感谢。
请参阅教程的“进一步阅读”部分。
你好 Jason,
我可以在自动编码器上使用 ReLU 吗?
在隐藏层中,是的。
叙述得很好。
谢谢!
非常简洁明了的解释!
谢谢!
作为一个曾经深度参与反向传播早期阶段,但已脱离该领域多年的人,我对 ReLU 方法有几个疑问。也许你可以解释一下。
1. ReLU 方法使梯度消失问题变得更糟,因为对于所有负值,导数都恰好为零。是的,您提到了补救方法,但它们不是 ReLU。
2. MLP 能够逼近任意函数,仅是因为激活函数的非线性(否则它们会退化为单层感知机)。这里的非线性集中在一个点——其他地方激活都是线性的。表达能力牺牲了多少?
3. 反向传播依赖于定义的导数——ReLU 在零处的导数未定义(我看到有人在那里使用零,这是左侧导数,因此是有效的次导数,但它仍然混淆了反向传播的解释)。
4. 正如您提到的(但这并非“神奇”,可以证明这是收敛速度与 Hessian 的最高特征值成正比的结果),与 [0,1] 和 Logistic 激活相比,使用平均值为零的输入值和 tanh 激活,收敛速度要好得多。ReLU 是一种 Logistic 激活。
谢谢
感谢分享您对 ReLU 的顾虑。也许与 sigmoid/tanh 相比,ReLU 取得的成果不言自明?
你好 jason,
也许对这个帖子发表评论太晚了,但您能告诉我们网络是如何学习的吗?我的意思是,假设我们有一个圆的图像,那么它是如何识别图像的?我的意思是,我们试图匹配的期望输出是什么,整个过程是如何工作的?非常感谢您关于激活函数的精彩帖子。
好问题,也许可以从这个教程开始
https://machinelearning.org.cn/tutorial-first-neural-network-python-keras/
非常有好的渐进式解释!
谢谢!
哇,非常好的教程,非常感谢。这真的有助于像我这样刚开始学习 ANN 等的人。我唯一的抱怨是,对 sigmoid 和 tanh 缺点的解释有点含糊,而且 L1 和 L2 正则化方法也没有描述,至少是简要描述。另外,最好能一起绘制 sigmoid、tanh 和 ReL 的图,以便进行比较和对比。
谢谢。
很棒的建议!
嗨,Jason,
感谢您的解释。很棒的文章。我遇到了 ReLU 的另一个优点,即“噪声鲁棒性非激活状态”,以及 LReLU 或 PReLU 等其他激活函数,我读到“非激活状态对噪声不鲁棒”。
您能否解释一下这个概念?另外,“非激活状态”和“噪声鲁棒性”是什么意思?
谢谢。
也许可以问您“遇到”的解释的作者?
嗨,Jason,
早上好
您能否就以下问题提供您的专家建议?
在 SIGMOID 激活函数中,它的输出是 0 或 1,当它为零时,相应的神经元将不会被激活。那么为什么 SIGMOID 不是稀疏激活函数?
谢谢
不,sigmoid 的输出是介于 0 和 1 之间的值,而不是 0 或 1。
嗨,Jason,
谢谢你的回复。
SIGMOID 的范围是 0 到 1。但它的输出可以是 0。在这种情况下,它就是稀疏的。
请告知您的建议。
是的,它可以为零,如果你有很多零,它就会是稀疏的。
在 SIGMOID 激活函数中,如果输出小于阈值,例如 0.5,则输出转换为 0,然后相应的神经元不会被激活。那么我认为网络将变得稀疏。您能解释一下吗?
为什么近似为“0”不是稀疏?
谢谢
这取决于输入的性质。
AttributeError: ‘Activation’ object has no attribute ‘get_output’。这是在以下情况下发生的:
“””””
output_layer = model.layers[1].get_output()
output_fn = theano.function([model.layers[0].get_input()], output_layer)
“””””
您能告诉我 model.layers.get_output() 属性的替代方案是什么吗?
抱歉,我以前没见过这个问题。也许可以试试发到 stackoverflow?
很棒的解释!????
干得好!
嗨,Jason,
我有一个疑问。
最近,我学习了一个使用 sigmoid 函数的回归问题。原因在于,它计算的实体本质上是从连续数据中从 0 到 1 的分数表示的,这就是为什么使用了 sigmoid 函数。
另外,该解决方案没有使用 0.5 阈值来获取二元类别,它只是想要从 0 到 1 的概率值范围。我很好地理解了这一点。另外,结果在预测过程中是令人满意的。
现在,令人困惑的是,它仍然使用了均方误差作为损失函数。所以我感到困惑,因为
我读到对数损失是 sigmoid 激活函数的成本函数。
我的问题是:上述情况中可以做些什么来使结果良好?
一直以来,谢谢。
Tanuja
您描述的模型听起来并非不合理。
你好 Jason,我没明白。你的意思是模型不合理吗?谢谢!
抱歉,我的意思是模型在我看来是很好的。
谢谢 Jason。
您能否详细解释一下为什么在这种描述的情况下,使用 MSE 而不是对数损失指标仍然可以?
在我对互联网的搜索中,我发现 sigmoid 搭配对数损失指标比 MSE 指标对错误分类的惩罚更大。
那么,我是否可以理解,我们有兴趣知道 0 到 1 之间的值,而不是两个类别这一事实,可以证明 MSE 指标的使用是合理的?
任何解释都值得赞赏。
将 sigmoid 激活用于回归问题并非理想选择,但它会将您的输出限制在 [0,1] 的范围内,这在某些应用中是可取的。
也许可以尝试一下,并与线性激活的结果进行比较。
在此处了解更多关于损失函数的信息
https://machinelearning.org.cn/how-to-choose-loss-functions-when-training-deep-learning-neural-networks/
嗨,Jason,
一如既往,精彩的帖子!我从您那里学到了很多东西:)
我有一个关于激活函数和 LSTM 的问题(我正在尝试为二元分类构建 LSTM 网络)。LSTM 单元内部已经有 4 个具有激活函数(sigmoid/tanh)的神经网络层。我想知道,LSTM 网络是否必须具有激活函数或循环激活函数,因为这些 sigmoid 和 tanh 已经存在于单元内部?在许多博客/教程中,我发现人们将 ReLU 用于 LSTM,但我想知道为什么?既然单元输出是 sigmoid 和 tanh 的乘积,那么在之后使用 ReLU 是否很奇怪?此外,LSTM 不会陷入梯度消失问题,所以我不太理解使用它的优势。您提到的参考文献使用了带有 ReLU 的 RNN 而不是 LSTM,因此我没有找到我的答案。
在另一个博客(https://machinelearning.org.cn/how-to-develop-rnn-models-for-human-activity-recognition-time-series-classification/)中,您没有为 LSTM 指定任何激活函数,这意味着您使用了 Keras 的默认值。您使用此默认值(activation=tanh,recurrent activation=sigmoid)的原因是什么,或者您知道为什么它是默认值而不是没有(循环)激活函数吗?
谢谢!
默认值基于原始LSTM论文,在许多情况下效果都很好。
我认为在某些时间序列问题中使用ReLU激活函数在LSTM中很有用。
也许可以尝试每种方法并为您的特定数据集进行比较,然后使用效果最好/误差最低的方法。
非常感谢!我将尝试ReLu和默认值。再说一件事,以确保我理解您所说的。我已经在网上搜索了所有内容,所以如果您知道以下信息,那将非常有帮助:
您说默认值基于原始论文。那么Keras中的recurrent_activation(sigmoid)是指LSTM单元中的门使用的sigmoid吗?而Keras中的activation(tanh)是指在与输出门相乘并输出之前,单元状态所经过的tanh吗?如果属实,那么更改默认的Keras激活就相当于改变了Hochreiter设计的原始LSTM单元结构本身?那么,如果我想使用原始设计的LSTM,我不应该更改Keras中的函数(从而使用Keras的默认值)?还是这不正确,Keras中的激活函数是在原始设计的LSTM单元(包含其sigmoid和tanh)之上增加了一个额外的激活?
希望你能帮帮我!!!
祝好
正确。默认情况下,它是标准的LSTM,将激活更改为relu与标准LSTM略有不同。
太好了!谢谢:)
不客气。
嗨,Jason,
非常感谢您提供的精彩文章。您能否告诉我ReLU(max= (0, x))中x的最大值,以及PReLU(max(alpha * x, x))中alpha和x的最大值是多少?这将对我非常有帮助。
非常感谢!
没有最大值。
感谢Jason的详细解释。
不客气。
嗨,Jason,
感谢您的精彩解释。
我有一个问题。
是否存在任何已知的激活函数f,使得以下属性成立
x1-x2 < = y1-y2 暗示 f(x1)-f(x2 ) < = f(y1)-f(y2)
谢谢!
不知道,抱歉。也许可以将这个问题发布到数学堆栈交换。
层中的ReLU神经元向前连接到下一层中的n个权重。
当神经元处于激活状态时(f(x)=x),由权重定义的模式以强度x投射到下一层。当神经元关闭时(f(x)=0),当然没有任何投射,就像权重不存在一样。
然后,神经元可以根据x>=0或不根据x的状态,处于以下两种状态之一。
如果在神经网络中将权重数量加倍,那么在x<0时,可以不是投射零,而是用另一组权重投射一个不同的模式,其强度为x。
然后,激活函数始终为f(x)=x(不做任何操作),但会在两个前向连接的权重向量之间进行组合切换。
https://discourse.processing.org/t/relu-is-half-a-cookie/32134
感谢分享。
ReLU函数(又称斜坡函数)几乎在所有地方都是可微的,除了x=0。其导函数是众所周知的Heaviside阶跃函数,该函数在电子学和物理学中广泛用于描述“正在切换的事物”。Heaviside函数在泛函分析中表现得非常好,例如拉普拉斯变换。根据约定,在x=0处,其值为1/2。
最快的Python ReLU是将它嵌入到lambda中
relu = lambda x : x if x > 0 else 0
确实,你也可以写成 relu = lambda x: max(x,0)
ELU对于负输入仍然存在潜在的饱和问题。但它是否比sigmoid更可取,因为只有一边可能饱和?
PReLU似乎没有这样的问题。它是否可能比ELU更受欢迎?
嗨Siegfried……以下信息可能有助于您为给定的模型选择激活函数。
https://machinelearning.org.cn/choose-an-activation-function-for-deep-learning/
ReLU激活函数解决了梯度消失问题,使模型能够更快地学习并获得更好的性能。
我认为你漏掉了“leaky”
嗨 me……你说得对!Rectified Linear Unit(ReLU)激活函数确实有助于克服梯度消失问题,但它可能会遇到“死亡ReLU”问题,即神经元可能变得不活跃,如果它们卡在函数的负区域,就会停止学习。
Leaky Rectified Linear Unit(Leaky ReLU)是一个扩展,它通过在输入为负时允许一个小的、非零的梯度来解决这个问题,这有助于防止神经元死亡。以下是两者的简要说明:
### ReLU(Rectified Linear Unit)
\[ f(x) = \max(0, x) \]
– **优点**:简单,计算效率高,有助于缓解梯度消失问题。
– **缺点**:可能遇到死亡ReLU问题,即神经元在训练过程中卡住,并始终对任何输入输出0。
### Leaky ReLU
\[ f(x) = \begin{cases}
x & \text{如果 } x > 0 \\
\alpha x & \text{否则}
\end{cases} \]
其中 \( \alpha \) 是一个小的常数,通常为 \( 0.01 \)。
– **优点**:通过在 \( x < 0 \) 时允许一个小的、非零的梯度来解决死亡ReLU问题。– **缺点**:比ReLU稍复杂,但仍具有计算效率。### 代码实现以下是在TensorFlow/Keras中实现和使用ReLU和Leaky ReLU的方法:
pythonimport tensorflow as tf
from tensorflow.keras.layers import Dense, LeakyReLU
# 使用ReLU的模型示例
model_relu = tf.keras.models.Sequential([
Dense(64, input_shape=(100,), activation='relu'),
Dense(64, activation='relu'),
Dense(1, activation='sigmoid')
])
# 使用Leaky ReLU的模型示例
model_leaky_relu = tf.keras.models.Sequential([
Dense(64, input_shape=(100,)),
LeakyReLU(alpha=0.01),
Dense(64),
LeakyReLU(alpha=0.01),
Dense(1, activation='sigmoid')
])
# 编译模型
model_relu.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])
model_leaky_relu.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])
在这些示例中,
model_relu使用标准的ReLU激活函数,而model_leaky_relu使用Leaky ReLU激活函数。### 实际考虑
– **ReLU**:当您想要一个简单、快速且通常有效的激活函数时使用。请注意死亡ReLU问题。
– **Leaky ReLU**:当您在网络中遇到死亡ReLU问题时使用,因为它可以帮助保持梯度流动并改善学习。
ReLU和Leaky ReLU都是深度学习中的流行选择,知道何时使用它们可以帮助优化模型的性能。