您不必按原样对时间序列预测问题进行建模。
有许多方法可以重构您的预测问题，既可以简化预测问题，又可能暴露更多或不同的信息供建模。重构最终可以带来更好和/或更稳健的预测。
在本教程中，您将使用 Python 了解如何重构您的时间序列预测问题。
完成本教程后，您将了解：
- 如何将您的时间序列预测问题重构为另一种回归问题。
- 如何将您的时间序列预测问题重构为分类预测问题。
- 如何使用替代时间范围重构您的时间序列预测问题。
通过我的新书 《Python 时间序列预测入门》 启动您的项目，书中包含分步教程和所有示例的Python源代码文件。
让我们开始吧。
- 2019 年 4 月更新：更新了数据集链接。
- 2019年8月更新：更新了数据加载以使用新的API。
如何重构你的时间序列预测问题
照片来源：Sean MacEntee，部分权利保留。
重构问题的优势
重构问题是指探索对要预测的内容的替代视角。
探索时间序列预测问题的替代框架有两个潜在优势
- 简化您的问题。
- 为集成预测提供基础。
这两项优势最终都会导致更具技能和/或更稳健的预测。
1. 简化您的问题
在预测项目上，最大的收益或许来自于对问题的重构。
这是因为预测问题的结构和类型比数据转换、模型选择或模型超参数的选择有更大的影响。
它是项目中最大的杠杆，必须仔细考虑。
2. 集成预测
除了改变您正在处理的问题之外，重构还有另一个作用：它可以为您提供一套不同但高度相关的问题，供您建模。
这样做的优点是，框架可能足够不同，以至于需要不同的数据准备和建模方法。
对同一问题的不同视角的模型可能会从输入中捕获不同的信息，从而产生有技能但方式不同的预测。这些预测可以集成在一起，从而产生更具技能或更稳健的预测。
在本教程中，我们将探讨您可以考虑重构时间序列预测问题的三种不同方式。
在深入探讨之前，让我们先看一个预测每日最低温度的简单单变量时间序列问题，作为讨论的背景。
停止以**慢速**学习时间序列预测！
参加我的免费7天电子邮件课程，了解如何入门（附带示例代码）。
点击注册，同时获得该课程的免费PDF电子书版本。
日最低气温数据集
此数据集描述了墨尔本市 10 年（1981-1990 年）的每日最低气温。
单位是摄氏度，共有3650个观测值。数据来源归功于澳大利亚气象局。
将“daily-minimum-temperatures.csv”下载到您当前的工作目录。
下面的示例将数据集加载为 Pandas Series。
|
1 2 3 4 5 6 |
from pandas import read_csv from matplotlib import pyplot series = read_csv('daily-minimum-temperatures.csv', header=0, index_col=0) print(series.head()) series.plot() pyplot.show() |
运行示例将打印加载的数据集的前 5 行。
|
1 2 3 4 5 6 |
日期 温度 1981-01-01 20.7 1981-01-02 17.9 1981-01-03 18.8 1981-01-04 14.6 1981-01-05 15.8 |
还将创建一个时间序列的折线图。
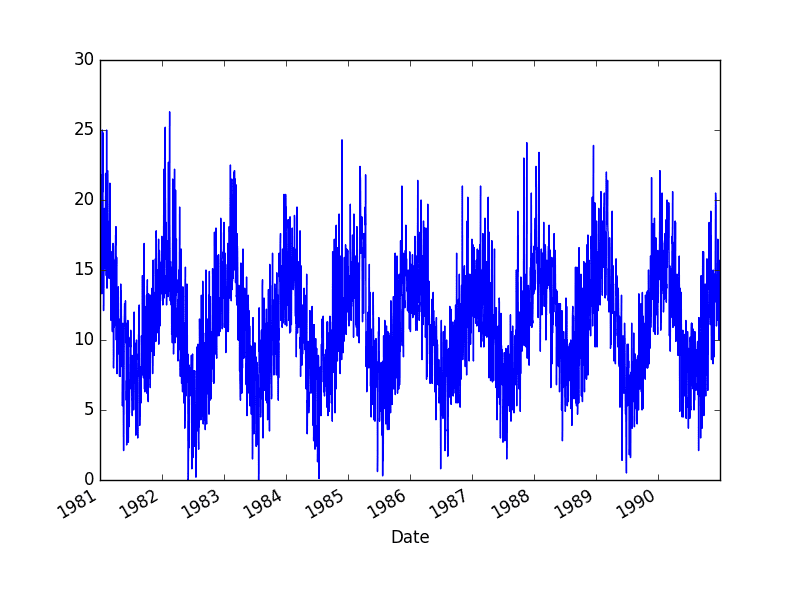
每日最低温度数据集
朴素时间序列预测
朴素方法是按原样预测问题。
作为参考，我们将此称为朴素时间序列预测。
在这种情况下，可以删除季节性信息，使序列具有季节性平稳性。
然后可以根据滞后观测值的某个函数来对时间序列进行建模。
例如
|
1 |
Temp(t+1) = B0 + B1*Temp(t-1) + B2*Temp(t-2) ... Bn*Temp(t-n) |
其中Temp(t+1)是序列中要预测的下一个温度，B0到Bn是从训练数据中学习到的系数，Temp(t-1)到Temp(t-n)是滞后观测值。
这对于许多问题来说可能没问题，甚至可能是必需的。
风险在于，对如何重构问题的先入为主的观念影响了数据收集，从而可能限制了结果。
回归重构
大多数时间序列预测问题是回归问题，需要预测实值输出。
以下是这个问题可以重构为另一种回归问题的 5 种不同方式
- 预测与前一天相比的最低温度变化。
- 预测最低温度相对于过去 14 天平均值的变化。
- 预测最低温度相对于去年同期的平均值。
- 预测最低温度四舍五入到最接近的 5 摄氏度。
- 预测未来 7 天的平均最低温度。
使温度相对化是一种线性变换，可能不会使问题更简单、更容易预测，但它可能会启发新的想法，甚至新的数据源供您考虑。
它还有助于您更清晰地思考预测将如何使用，以及对该预测值的硬性要求实际上是什么。
转换预测问题的粒度确实会改变问题的难度，如果问题的要求允许此类重新定义，则可能非常有用。
以下是重构每日最低温度预测问题以预测四舍五入到最接近的 5 度的每日温度的示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
from pandas import read_csv from pandas import DataFrame 从 pandas 导入 concat from math import floor # 加载数据 series = read_csv('daily-minimum-temperatures.csv', header=0, index_col=0) # 创建滞后数据集 values = DataFrame(series.values) dataframe = concat([values.shift(1), values], axis=1) dataframe.columns = ['t-1', 't+1'] # 四舍五入预测到最近的 5 for i in range(len(dataframe['t+1'])): dataframe['t+1'][i] = int(dataframe['t+1'][i] / 5) * 5.0 print(dataframe.head(5)) |
运行示例将打印重构问题的前 5 行。
该问题定义为：给定前一天的最低温度，预测最接近 5 度的最低温度。
|
1 2 3 4 5 6 |
t-1 t+1 0 NaN 20.0 1 20.7 15.0 2 17.9 15.0 3 18.8 10.0 4 14.6 15.0 |
分类重构
分类涉及预测类别或标签输出（如“冷”和“热”）。
以下是这个问题可以重构为分类问题的 5 种不同方式
- 预测最低温度是冷、中等还是热。
- 预测最低温度的变化是小还是大。
- 预测最低温度是否为月度最低。
- 预测最低温度是否会高于或低于去年同期的最低温度。
- 预测未来 7 天最低温度是上升还是下降。
转向分类可以简化预测问题。
这种方法为标签和二元分类框架带来了新的想法。
输出变量的原生回归表示意味着大多数分类框架可能会保留顺序结构（例如，冷、中等、热）。这意味着正在预测的类别之间存在有序关系，而预测“狗”和“猫”之类的标签时可能并非如此。
顺序关系允许硬分类问题以及整数预测问题，后者可以事后四舍五入到特定类别。
以下是将每日最低温度预测问题转换为分类问题的示例，其中每个温度值都是冷、中等或热的有序值。这些标签映射到整数值，定义为
- 0（冷）：< 10 摄氏度。
- 1（中等）：>= 10 且 < 25 摄氏度。
- 2（热）：>= 25 摄氏度。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
from pandas import read_csv from pandas import DataFrame 从 pandas 导入 concat from math import floor # 加载数据 series = read_csv('daily-minimum-temperatures.csv', header=0, index_col=0) # 创建滞后数据集 values = DataFrame(series.values) dataframe = concat([values.shift(1), values], axis=1) dataframe.columns = ['t-1', 't+1'] # 四舍五入预测到最近的 5 for i in range(len(dataframe['t+1'])): value = dataframe['t+1'][i] if value < 10.0: dataframe['t+1'][i] = 0 elif value >= 25.0: dataframe['t+1'][i] = 2 else: dataframe['t+1'][i] = 1 print(dataframe.head(5)) |
运行示例将打印重构问题的前 5 行。
给定前一天最低温度（摄氏度），目标是将温度预测为冷、中等或热（分别为 0、1、2）。
|
1 2 3 4 5 6 |
t-1 t+1 0 NaN 1.0 1 20.7 1.0 2 17.9 1.0 3 18.8 1.0 4 14.6 1.0 |
时间范围重构
可以变化的另一个轴是时间范围。
时间范围是指要预测的未来时间步的数量。
以下是这个问题可以重构为不同时间范围的 5 种不同方式
- 预测未来 7 天的最低温度。
- 预测 30 天后的最低温度。
- 预测下个月的平均最低温度。
- 预测下周最低温度最低的那一天。
- 预测一年的最低温度值。
人们很容易陷入需要单步预测的想法中。
专注于围绕时间范围重构问题，会迫使您思考点预测与多步预测以及考虑多远的未来。
您也许可以预测到很远的未来，但技能可能会有所不同，未来预测得越远，技能下降得越厉害。在考虑预测范围时，还要考虑预测的最低可接受性能。
下面的示例将每日最低温度预测问题转换为预测未来 7 天最低温度的预测问题。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
from pandas import read_csv from pandas import DataFrame 从 pandas 导入 concat from math import floor # 加载数据 series = read_csv('daily-minimum-temperatures.csv', header=0, index_col=0) # 创建滞后数据集 values = DataFrame(series.values) dataframe = concat([values.shift(1), values, values.shift(-1), values.shift(-2), values.shift(-3), values.shift(-4), values.shift(-5), values.shift(-6)], axis=1) dataframe.columns = ['t-1', 't+1', 't+2', 't+3', 't+4', 't+5', 't+6', 't+7'] print(dataframe.head(14)) |
运行示例将打印转换数据集的前 14 条记录。
该问题定义为：给定前一天（摄氏度）的最低日温度，预测未来 7 天的最低日温度。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
t-1 t+1 t+2 t+3 t+4 t+5 t+6 t+7 0 NaN 20.7 17.9 18.8 14.6 15.8 15.8 15.8 1 20.7 17.9 18.8 14.6 15.8 15.8 15.8 17.4 2 17.9 18.8 14.6 15.8 15.8 15.8 17.4 21.8 3 18.8 14.6 15.8 15.8 15.8 17.4 21.8 20.0 4 14.6 15.8 15.8 15.8 17.4 21.8 20.0 16.2 5 15.8 15.8 15.8 17.4 21.8 20.0 16.2 13.3 6 15.8 15.8 17.4 21.8 20.0 16.2 13.3 16.7 7 15.8 17.4 21.8 20.0 16.2 13.3 16.7 21.5 8 17.4 21.8 20.0 16.2 13.3 16.7 21.5 25.0 9 21.8 20.0 16.2 13.3 16.7 21.5 25.0 20.7 10 20.0 16.2 13.3 16.7 21.5 25.0 20.7 20.6 11 16.2 13.3 16.7 21.5 25.0 20.7 20.6 24.8 12 13.3 16.7 21.5 25.0 20.7 20.6 24.8 17.7 13 16.7 21.5 25.0 20.7 20.6 24.8 17.7 15.5 |
总结
在本教程中，您学习了如何使用 Python 重构您的时间序列预测问题。
具体来说，你学到了：
- 如何为您的时间序列问题设计替代回归表示。
- 如何将您的预测问题构建为分类问题。
- 如何为您的预测问题设计替代时间范围。
您知道其他重构时间序列预测问题的方法吗？
在下面的评论中分享它们？
你有什么问题吗？
在下面的评论中提问，我会尽力回答。
想用Python开发时间序列预测吗？
几分钟内开发您自己的预测
...只需几行python代码在我的新电子书中探索如何实现
Python 时间序列预测入门
它涵盖了**自学教程**和**端到端项目**，主题包括：*数据加载、可视化、建模、算法调优*等等。
最终将时间序列预测带入
您自己的项目
跳过学术理论。只看结果。
非常有用的，非常感谢！
很高兴听到这个消息。
嘿 Jason，我喜欢你的网站，我每天都访问它，你有什么关于如何避免 Y-1 问题的方法吗？当模型只预测最后一个值加上某个常数，而我最终得到一个滞后且无法使用的序列。
是的，首先尝试移除趋势/季节性，然后查看 ACF/PACF 图，看看是否有可以学习的内容。
如果在测试了一系列方法后，您无法做得比持久性更好，那么您可能正在处理一个随机游走。
如果除了值之外，您还有其他特征，比如湿度、风速等怎么办？
您也可以对它们进行建模。