如何在 Weka 中完成一个回归机器学习项目

上手应用机器学习最快的方法就是通过端到端的项目进行练习。

在这篇文章中，你将了解到如何在Weka中完成一个回归问题的端到端项目。读完这篇文章，你将知道：

• 如何在Weka中加载和分析回归数据集。
• 如何创建数据的多个不同转换视图，并在每个视图上评估一系列算法。
• 如何最终确定模型并呈现结果，以便对新数据进行预测。

通过我新书《Weka机器学习精通》来启动你的项目，书中包含分步教程和所有示例的清晰截图。

让我们开始吧。

Weka回归机器学习项目分步教程
照片作者：vagawi，部分权利保留。

教程概述

本教程将引导你完成在Weka中完成机器学习项目所需的关键步骤。

我们将完成以下步骤：

1. 加载数据集。
2. 分析数据集。
3. 准备数据集的视图。
4. 评估算法。
5. 调整算法性能。
6. 评估集成算法。
7. 呈现结果。

1. 加载数据集

Weka安装目录的data/文件夹中可用的回归问题选择很少。回归是一种重要的预测建模问题类别。请从UCI机器学习知识库下载免费的回归问题附加包。

它可以在Weka网页的数据集页面找到，并且是列表中第一个，名为

• 一个包含37个回归问题的jar文件，来源于各种来源（datasets-numeric.jar）

这是一个.jar文件，是Java存档的压缩类型。你应该能够用大多数现代解压程序解压它。如果你安装了Java（使用Weka很可能需要它），你也可以在下载jar文件的目录中使用以下命令在命令行上手动解压.jar文件：

解压文件后，会创建一个名为numeric的新目录，其中包含37个ARFF格式的原生Weka回归数据集。

在本教程中，我们将处理波士顿房价数据集。

在这个数据集中，每个实例描述了波士顿郊区的属性，任务是预测房价（以千美元为单位）。有13个数值型输入变量，具有不同的尺度，描述了郊区的属性。你可以在UCI机器学习知识库上了解更多关于这个数据集的信息。

1. 打开Weka GUI Chooser
2. 点击“Explorer”按钮打开Weka Explorer。
3. 点击“Open file…”按钮，导航到numeric/目录，然后选择housing.arff。点击“Open”按钮。

数据集现已加载到 Weka 中。

Weka加载波士顿房价数据集

2. 分析数据集

在开始建模之前，检查数据非常重要。

检查每个属性的分布以及属性之间的交互作用，可能会为我们可能使用的数据转换和建模技术提供线索。

描述性统计

在“Current relation”窗格中查看数据集的详细信息。我们可以注意到几点：

• 数据集名为housing。
• 有506个实例。如果稍后使用10折交叉验证来评估算法，那么每折将包含约50个实例，这已经足够了。
• 有14个属性，13个输入属性和1个输出属性。

点击“Attributes”窗格中的每个属性，并查看“Selected attribute”窗格中的摘要统计信息。

我们可以注意到我们数据的一些事实：

• 所有属性都没有缺失值。
• 除了一个二元属性外，所有输入属性都是数值型，并且具有不同的取值范围。
• 最后一个属性是输出变量，名为class，它是数值型的。

我们可能会从归一化或标准化数据中获益。

属性分布

点击“Visualize All”按钮，让我们来查看每个属性的图形分布。

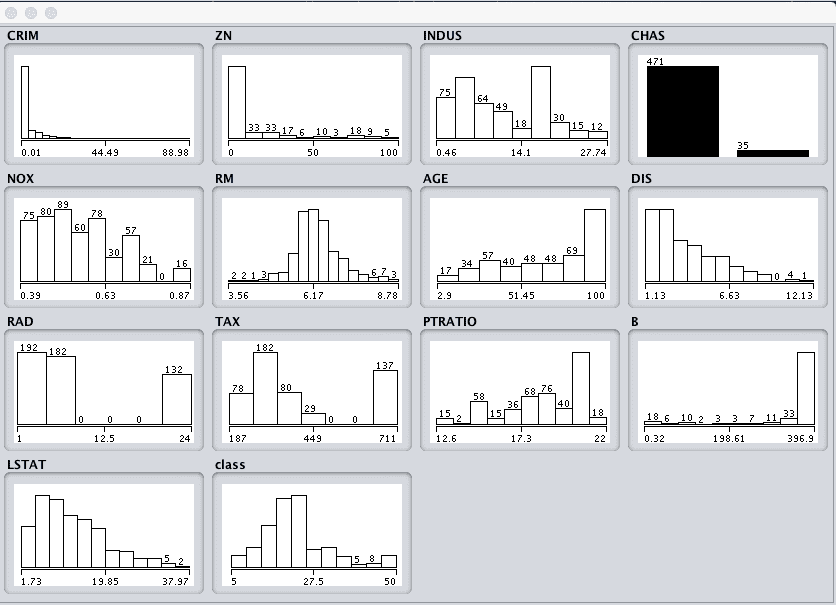
Weka波士顿房价单变量属性分布

我们可以注意到数据形状的一些特点：

• 我们可以看到属性具有不同的分布范围。
• CHAS属性看起来像是一个二元分布（两个值）。
• RM属性看起来具有高斯分布。

使用决策树等非线性回归方法可能比使用线性回归等线性回归方法更有优势。

属性交互

点击“Visualize”选项卡，让我们来查看属性之间的一些交互。

1. 将“PlotSize”减小到50，并调整窗口大小，以便所有图表都可见。
2. 将“PointSize”增加到 3，使点更容易看到。
3. 点击“Update”按钮应用更改。

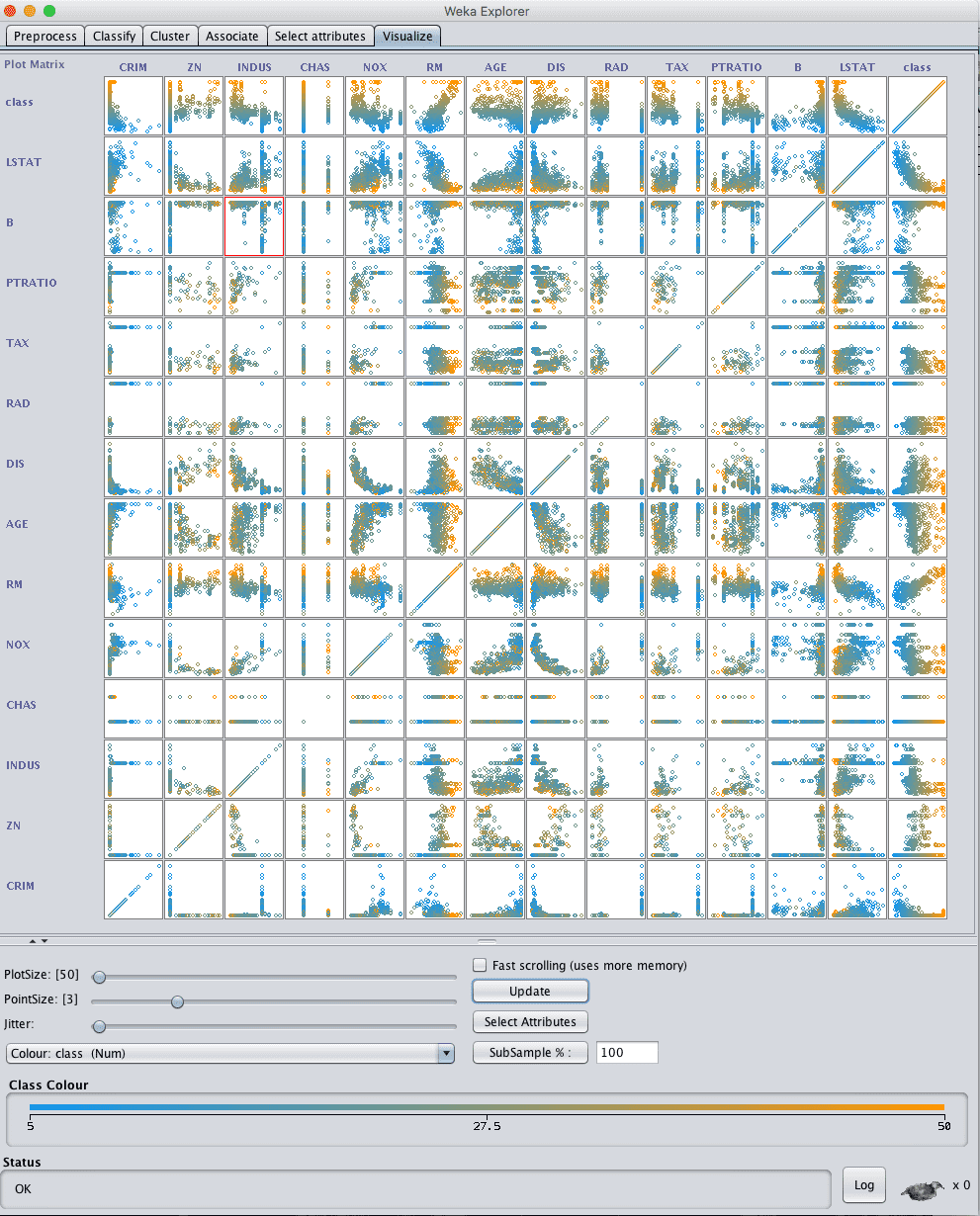
Weka波士顿房价散点图矩阵

纵观这些图表，我们可以看到一些结构化的关系，这些关系可能有助于建模，例如DIS与NOX以及AGE与NOX之间的关系。

我们还可以看到输入属性与输出属性之间的一些结构化关系，例如LSTAT与CLASS，以及RM与CLASS。

3. 准备数据集的视图

在本节中，我们将创建一些不同的数据集视图，以便在下一节评估算法时，能够了解哪些视图在将回归问题的结构暴露给模型方面通常更好。

我们将首先创建一个原始housing.arff数据文件的修改副本，然后进行3个附加的数据转换。我们将从原始文件的修改副本中创建数据集的每个视图，并将其保存到新文件中，以供后续实验使用。

修改副本

CHAS属性是标称型（二元）的，值为“0”和“1”。

我们想创建一个原始housing.arff数据文件的副本，并将CHAS更改为数值属性，以便所有输入属性都为数值型。这将有助于转换和建模数据集。

找到housing.arff数据集，并在同一目录中创建一个名为housing-numeric.arff的副本。

在文本编辑器中打开这个修改后的文件housing-numeric.arff，滚动到定义属性的地方，特别是第56行定义的CHAS属性。

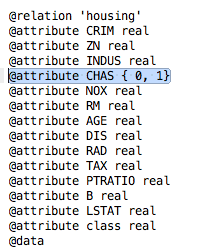
Weka波士顿房价属性数据类型

将CHAS属性的定义从

推广到

CHAS属性现在是数值型而不是标称型。这个修改后的数据集副本housing-numeric.arff将作为基准数据集。

Weka波士顿房价数据集（数值型数据类型）

归一化数据集

我们将创建的第一个视图是所有输入属性都归一化到0到1的范围。这可能有利于许多可能受属性尺度影响的算法，例如回归和基于实例的方法。

1. 打开Weka Explorer。
2. 打开修改后的数值数据集housing-numeric.arff。
3. 在“Filter”窗格中点击“Choose”按钮，然后选择“unsupervised.attribute.Normalize”过滤器。
4. 点击“Apply”按钮应用过滤器。
5. 点击“Attributes”窗格中的每个属性，并在“Selected attribute”窗格中查看最小值和最大值，以确认它们是0和1。
6. 点击“Save…”按钮，导航到一个合适的目录，然后输入一个合适的名称作为这个转换后的数据集，例如“housing-normalize.arff”。
7. 关闭Explorer界面。

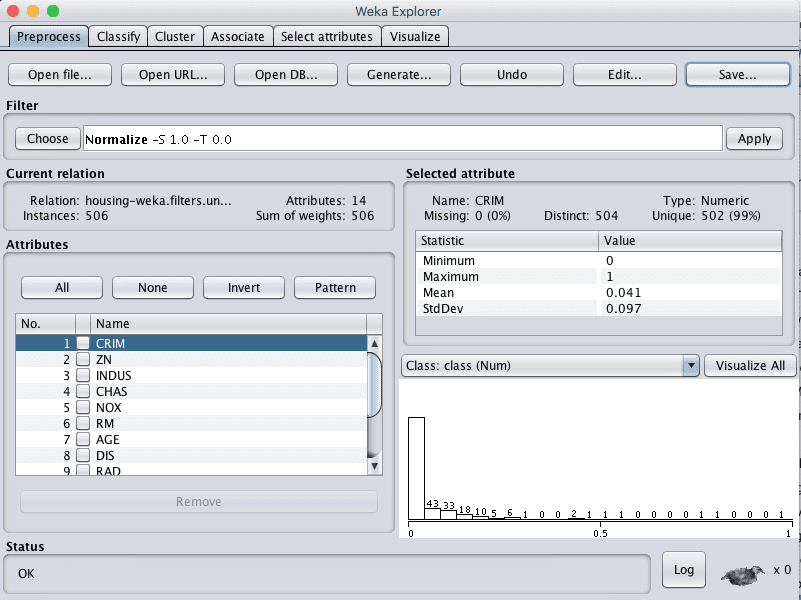
Weka波士顿房价数据集归一化数据过滤器

标准化数据集

我们在上一节中注意到，有些属性具有类似高斯分布的分布。我们可以通过使用标准化过滤器来重新调整数据并考虑这种分布。

这将创建一个数据集的副本，其中每个属性的平均值为0，标准差（平均方差）为1。这可能有利于下一节中假设输入属性具有高斯分布的算法，如逻辑回归和朴素贝叶斯。

1. 打开Weka Explorer。
2. 打开修改后的数值数据集housing-numeric.arff。
3. 点击“Filter”窗格中的“Choose”按钮，然后选择“unsupervised.attribute.Standardize”过滤器。
4. 点击“Apply”按钮应用过滤器。
5. 点击“Attributes”窗格中的每个属性，并在“Selected attribute”窗格中查看平均值和标准差值，以确认它们分别是0和1。
6. 点击“Save…”按钮，导航到一个合适的目录，然后输入一个合适的名称作为这个转换后的数据集，例如“housing-standardize.arff”。
7. 关闭Explorer界面。

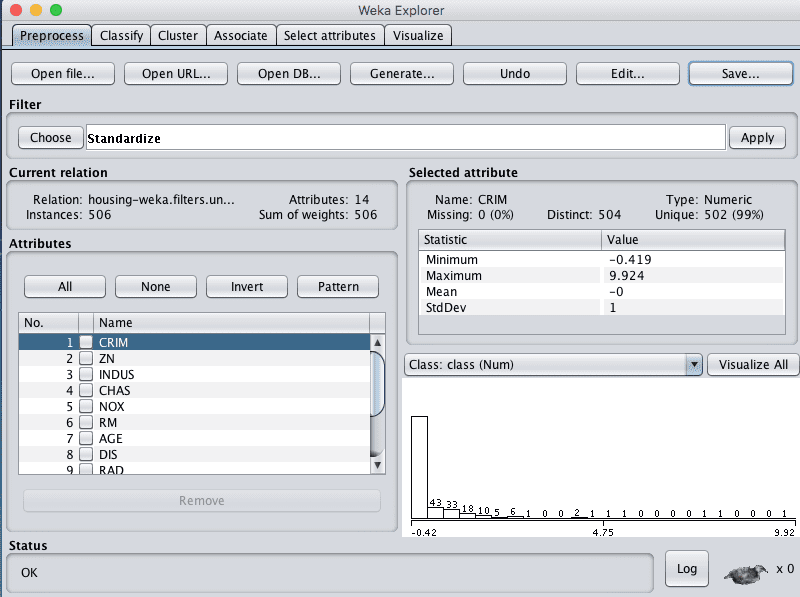
Weka波士顿房价数据集标准化数据过滤器

特征选择

我们不确定是否所有属性都真正需要用于进行预测。

在这里，我们可以使用自动特征选择来选择数据集中最相关的属性。

1. 打开Weka Explorer。
2. 打开修改后的数值数据集housing-numeric.arff。
3. 点击“Filter”窗格中的“Choose”按钮，然后选择“supervised.attribute.AttributeSelection”过滤器。
4. 点击“Apply”按钮应用过滤器。
5. 点击“Attributes”窗格中的每个属性，并查看选择的5个属性。
6. 点击“Save…”按钮，导航到一个合适的目录，然后输入一个合适的名称作为这个转换后的数据集，例如“housing-feature-selection.arff”。
7. 关闭Explorer界面。

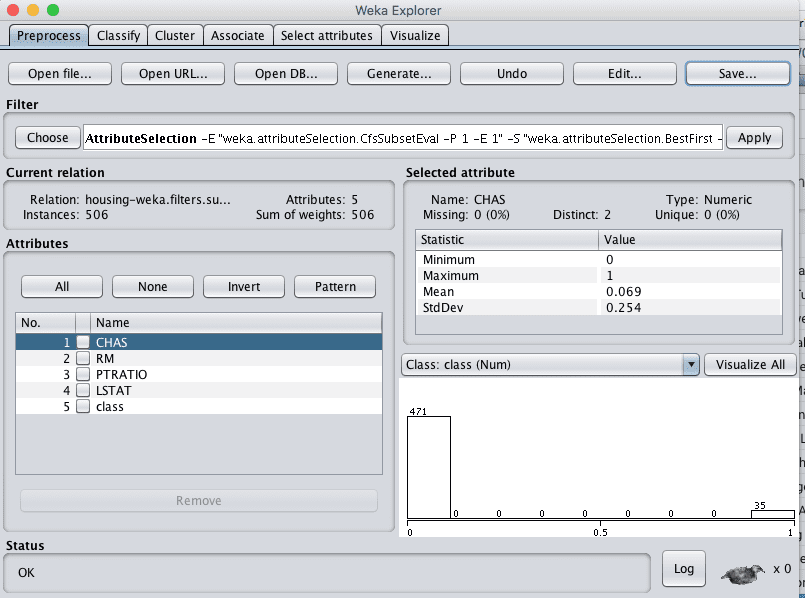
Weka波士顿房价数据集特征选择数据过滤器

4. 评估算法

让我们设计一个实验，在创建的不同数据集视图上评估一系列标准的分类算法。

1. 在Weka GUI Chooser上点击“Experimenter”按钮，启动Weka实验环境。

2. 点击“New”开始新实验。

3. 在“Experiment Type”窗格中，将问题类型从“Classification”更改为“Regression”。

4. 在“Datasets”窗格中点击“Add new…”，并选择以下4个数据集：

• housing-numeric.arff
• housing-normalized.arff
• housing-standardized.arff
• housing-feature-selection.arff

5. 在“Algorithms”窗格中点击“Add new…”，并添加以下8个多类别分类算法：

• rules.ZeroR
• bayes.SimpleLinearRegression
• functions.SMOreg
• lazy.IBk
• trees.REPTree

6. 在算法列表中选择IBK，然后点击“Edit selected…”按钮。

7. 将“KNN”从“1”更改为“3”，然后点击“OK”按钮保存设置。

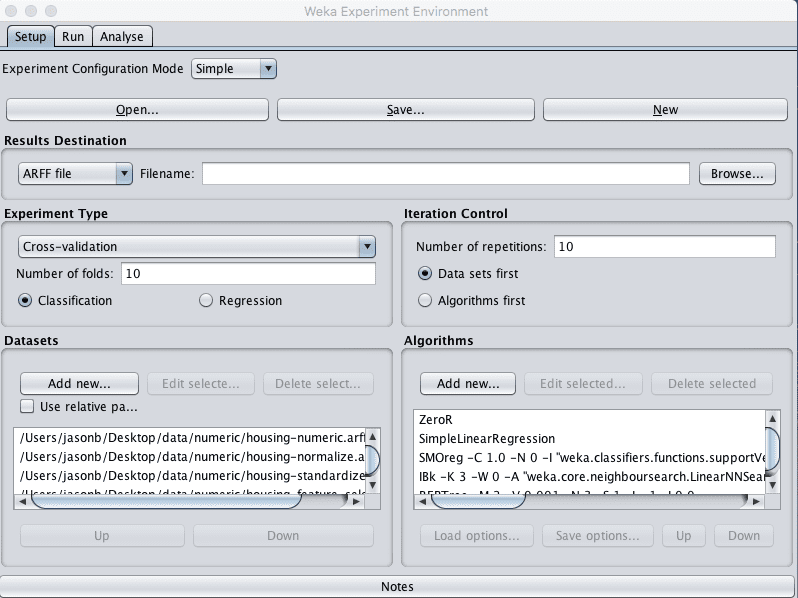
Weka波士顿房价算法比较实验设计

8. 点击“Run”打开Run选项卡，然后点击“Start”按钮运行实验。实验应该在几秒钟内完成。

9. 点击“Analyse”打开Analyse选项卡。点击“Experiment”按钮加载实验结果。

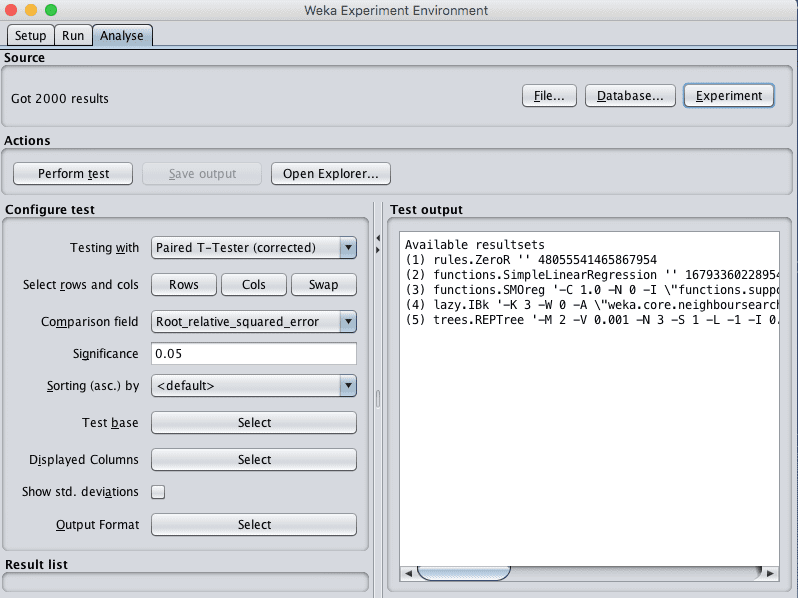
Weka波士顿房价数据集加载算法比较实验结果

10. 将“Comparison field”更改为“Root_mean_squared_error”。

11. 点击“Perform test”按钮，执行一个成对检验，将所有结果与ZeroR的结果进行比较。

请记住，RMSE越低越好。

这些结果很有说明性。

首先，我们可以看到所有算法都优于ZeroR的基线技能，并且差异是显著的（旁边有一个小“*”）。我们还可以看到，标准化或归一化数据似乎并没有为所评估的算法带来太多好处。

看起来，至少对于IBk来说，从选择更少特征的数据集视图中可能会看到一些小改进。

最后，看起来IBk (KNN) 可能是误差最低的。让我们进一步研究。

12. 点击“Test base”的“Select”按钮，然后选择lazy.IBk算法作为新的测试基准。

13. 点击“Perform test”按钮重新运行分析。

我们可以看到，IBk与其他算法之间存在显著差异，除了与REPTree算法和SMOreg的比较。IBk和SMOreg算法都是非线性回归算法，可以进一步调整，我们可以在下一节中对此进行研究。

5. 调整算法性能

在前一节算法评估中，我们确定了两个在问题上表现良好并适合进一步调整的算法：k近邻（IBk）和支持向量回归（SMOreg）。

在本节中，我们将设计实验来调整这两个算法，看看是否能进一步降低均方根误差。

我们将使用基准housing-numeric.arff数据集进行这些实验，因为该数据集的变体与其它视图相比，性能差异不大。

调整k近邻

在本节中，我们将调整IBk算法。具体来说，我们将研究使用不同的k值。

1. 打开Weka实验环境界面。

2. 点击“New”开始新实验。

3. 在“Experiment Type”窗格中，将问题类型从“Classification”更改为“Regression”。

4. 在“Datasets”窗格中添加housing-numeric.arff数据集。

5. 在“Algorithms”窗格中，添加lazy.IBk算法，并将“K”参数的值设置为1（默认值）。重复此过程，并添加以下IBk算法的额外配置：

• lazy.IBk，K=3
• lazy.IBk，K=5
• lazy.IBk，K=7
• lazy.IBk，K=9

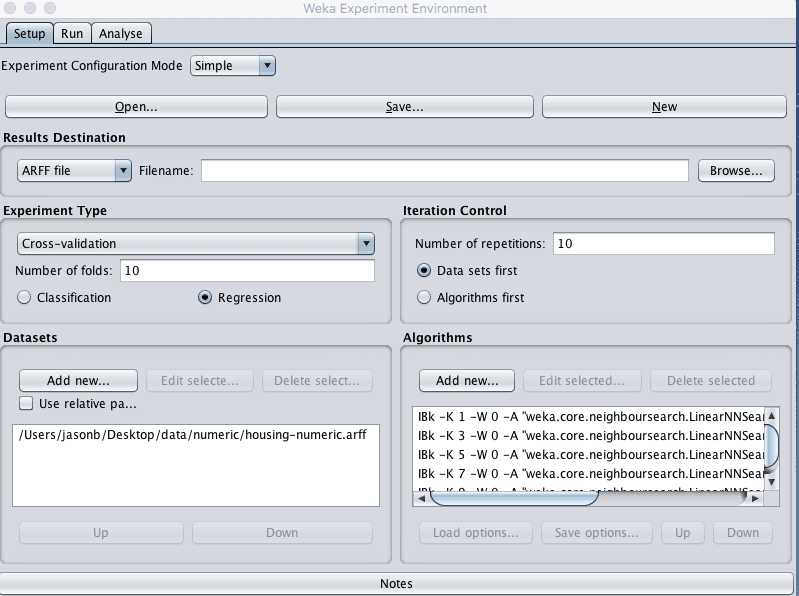
Weka波士顿房价数据集调整k近邻算法

6. 点击“Run”打开Run选项卡，然后点击“Start”按钮运行实验。实验应该在几秒钟内完成。

7. 点击“Analyse”打开Analyse选项卡。点击“Experiment”按钮加载实验结果。

8. 将“Comparison field”更改为“Root_mean_squared_error”。

9. 点击“Perform test”按钮执行成对检验。

我们发现K=3达到了最低误差。

10. 点击“Test base”的“Select”按钮，然后选择K=3的lazy.IBk算法作为新的测试基准。

11. 点击“Perform test”按钮重新运行分析。

我们可以看到，K=3与其他所有配置相比，差异显著且更优，除了K=1。我们了解到，通过调整IBk的k值，无法轻易获得显著的性能提升。

进一步的调整可以考虑使用不同的距离度量，或者使用数据集的不同视图（例如特征选择的视图）来调整IBk参数。

调整支持向量机

在本节中，我们将调整SMOreg算法。具体来说，我们将研究为多项式核函数使用不同的“exponent”（指数）值。

1. 打开Weka实验环境界面。

2. 点击“New”开始新实验。

3. 在“Experiment Type”窗格中，将问题类型从“Classification”更改为“Regression”。

4. 在“Datasets”窗格中添加housing-numeric.arff数据集。

5. 在“Algorithms”窗格中，添加functions.SMOreg算法，并将多项式核函数的“exponent”参数值设置为1（默认值）。重复此过程，并添加以下SMOreg算法的额外配置：

• functions.SMOreg, kernel=Polynomial, exponent=2
• functions.SMOreg, kernel=Polynomial, exponent=3

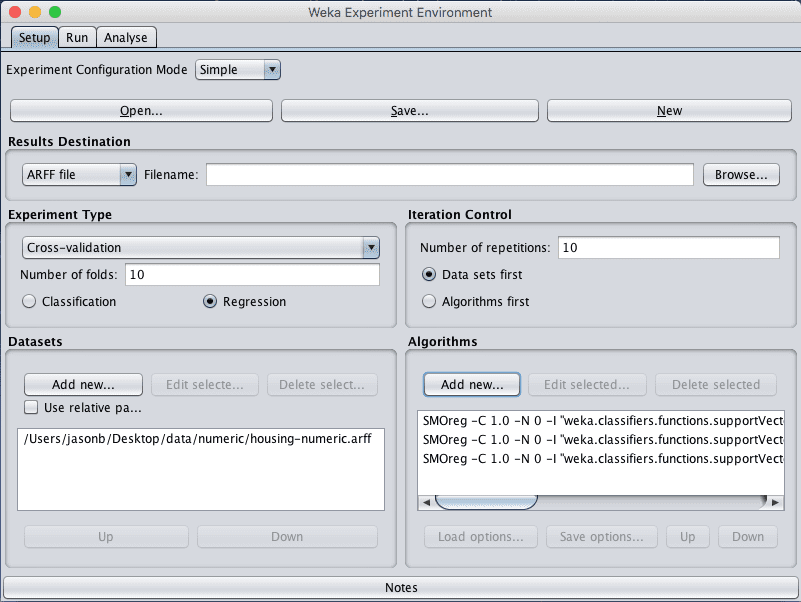
Weka波士顿房价数据集调整支持向量回归算法

6. 点击“Run”打开Run选项卡，然后点击“Start”按钮运行实验。根据系统的速度，实验大约需要10分钟才能完成。

7. 点击“Analyse”打开Analyse选项卡。点击“Experiment”按钮加载实验结果。

8. 将“Comparison field”更改为“Root_mean_squared_error”。

9. 点击“Perform test”按钮执行成对检验。

看起来exponent=3的核函数达到了最佳结果。将其设置为“Test base”并重新运行分析。

与exponent=1相比，exponent=3的结果在统计学上显著更好，但与exponent=2相比则不显著。两者都可以选择，尽管较低复杂度的exponent=2可能更快、更不容易出现问题。

6. 评估集成算法

在算法评估部分，我们注意到REPtree也取得了不错的结果，与IBk或SMOreg的性能没有统计学上的显著差异。在本节中，我们将考虑使用bagging的回归树的集成变体。

与上一节算法调整一样，我们将使用housing数据集的数值副本。

1. 打开Weka实验环境界面。

2. 点击“New”开始新实验。

3. 在“Experiment Type”窗格中，将问题类型从“Classification”更改为“Regression”。

4. 在“Datasets”窗格中添加housing-numeric.arff数据集。

5. 在“Algorithms”窗格中添加以下算法：

• trees.REPTree
• trees.RandomForest
• meta.Bagging

Weka波士顿房价数据集集成实验设计

6. 点击“Run”打开Run选项卡，然后点击“Start”按钮运行实验。实验应该在几秒钟内完成。

7. 点击“Analyse”打开Analyse选项卡。点击“Experiment”按钮加载实验结果。

8. 将“Comparison field”更改为“Root_mean_squared_error”。

9. 点击“Perform test”按钮执行成对检验。

10. 结果表明随机森林可能表现最佳。选择trees.RandomForest作为“Test base”，并重新运行分析。

这是非常令人鼓舞的，随机森林的结果是我们迄今为止在这个问题上看到的最好的结果，与Bagging和REPtree相比，差异是显著的。

为了总结，让我们选择RandomForest作为该问题的首选模型。

我们可以进行模型选择，并评估RandomForest的性能与K=1的IBk和exponent=3的SMOreg相比是否在统计学上显著。这留给读者作为练习。

11. 勾选“Show std. deviations”，显示结果的标准差。

12. 点击“Displayed Columns”的“Select”按钮，选择“trees.RandomForest”，点击“Select”确认选择。这将只显示Random Forest算法的结果。

13. 点击“Perform test”重新运行分析。

现在我们有了一个最终结果，可以用来描述我们的模型。

我们可以看到，模型在未见过数据上的估计误差为3.14（千美元），标准差为0.64。

7. 最终确定模型并呈现结果

我们可以创建模型的最终版本，该模型在所有训练数据上进行训练，并将其保存到文件中。

1. 打开Weka Explorer，加载housing-numeric.arff数据集。
2. 点击Classify。
3. 选择trees.RandomForest算法。
4. 将“Test options”从“Cross Validation”更改为“Use training set”。
5. 点击“Start”按钮创建最终模型。
6. 右键单击“Result list”中的结果项，然后选择“Save model”。选择一个合适的目录，并输入一个合适的名称，例如“housing-randomforest”作为模型。

然后可以在以后加载此模型，并用于对新数据进行预测。

我们可以使用上一节收集的模型准确率的均值和标准差来量化模型在未见过的数据上的估计准确率的预期变异性。

我们通常可以预期，模型在未见过数据上的性能将为3.14加上或减去（2 * 0.64）或1.28。我们可以将其重述为模型的误差将在千美元之间，介于1.86到4.42之间。

总结

在这篇文章中，你学习了如何使用Weka机器学习工作台完成一个回归机器学习问题。

具体来说，你学习了：

• 如何在Weka中加载、分析和准备数据集的视图。
• 如何使用Weka Experimenter评估一系列回归机器学习算法。
• 如何调整表现良好的模型并研究相关的集成方法以提升性能。

你对在Weka中处理回归机器学习问题或对此文章有任何疑问吗？请在下方评论区提出你的问题，我将尽力回答。

探索无需代码的机器学习！

在几分钟内开发您自己的模型

...只需几次点击

在我的新电子书中探索如何实现
使用 Weka 精通机器学习

涵盖自学教程和端到端项目，例如
加载数据、可视化、构建模型、调优等等...

最终将机器学习应用到你自己的项目中

跳过学术理论。只看结果。

查看内容