如何使用 Python 中的差分变换去除趋势和季节性

作者： Jason Brownlee 发布于 2020 年 6 月 23 日在时间序列深度学习 108 条评论

时间序列数据集可能包含趋势和季节性，在建模之前可能需要将其去除。

趋势可能导致随时间变化的均值，而季节性可能导致随时间变化的方差，两者都将时间序列定义为非平稳的。平稳数据集是指具有稳定均值和方差的数据集，因此更容易建模。

差分是一种流行且广泛使用的数据变换，用于使时间序列数据平稳。

在本教程中，您将学习如何使用 Python 将差分操作应用于您的时间序列数据。

完成本教程后，您将了解：

平稳时间序列和非平稳时间序列之间的对比，以及如何通过差分变换使时间序列平稳。
如何应用差分变换从序列中去除线性趋势。
如何应用差分变换从序列中去除季节性信号。

我的新书《时间序列深度学习预测》将助您启动项目，其中包括分步教程和所有示例的 Python 源代码文件。

让我们开始吧。

How to Remove Trends and Seasonality with a Difference Transform in Python

如何使用 Python 中的差分变换去除趋势和季节性
照片由 NOAA 拍摄，保留部分权利。

教程概述

本教程分为4个部分，它们是：

平稳性
差分变换
差分去除趋势
差分去除季节性

平稳性

时间序列不同于更传统的分类和回归预测建模问题。

时间结构为观察结果增加了顺序。这种强加的顺序意味着需要特别处理对这些观察结果一致性的重要假设。

例如，在建模时，假设观察结果的汇总统计量是一致的。在时间序列术语中，我们将这种期望称为时间序列的平稳性。

这些假设在时间序列中很容易被趋势、季节性和其他时间相关结构的添加而违反。

平稳时间序列

平稳时间序列中的观察结果不依赖于时间。

如果时间序列没有趋势或季节性效应，则它是平稳的。对时间序列计算的汇总统计量（例如观察结果的均值或方差）随时间保持一致。

当时间序列平稳时，更容易建模。统计建模方法假设或要求时间序列是平稳的。

非平稳时间序列

非平稳时间序列的观察结果显示出季节性效应、趋势以及其他依赖于时间索引的结构。

均值和方差等汇总统计量随时间变化，导致模型可能试图捕获的概念发生漂移。

经典时间序列分析和预测方法通过识别和去除趋势以及去除平稳效应来使非平稳时间序列数据平稳。

使序列数据平稳

您可以通过查看序列随时间变化的折线图来检查您的时间序列是否平稳。

序列中明显的趋势、季节性或其他系统结构是序列非平稳的指标。

更准确的方法是使用统计检验，例如迪基-富勒检验。

您应该使您的时间序列平稳吗？

一般来说，是的。

如果您的时间序列中存在明显的趋势和季节性，则对这些成分进行建模，从观测中去除它们，然后对残差训练模型。

如果我们对数据拟合一个平稳模型，我们假设我们的数据是平稳过程的实现。因此，我们分析的第一步应该是检查是否存在任何趋势或季节性效应的证据，如果存在，则将其去除。

—— 第 122 页，《R 语言时间序列入门》。

统计时间序列方法甚至现代机器学习方法都将受益于数据中更清晰的信号。

时间序列深度学习需要帮助吗？

立即参加我为期7天的免费电子邮件速成课程（附示例代码）。

点击注册，同时获得该课程的免费PDF电子书版本。

差分变换

差分是转换时间序列数据集的一种方法。

它可以用于去除序列对时间的依赖性，即所谓的时间依赖性。这包括趋势和季节性等结构。

差分可以通过去除时间序列水平的变化来帮助稳定时间序列的均值，从而消除（或减少）趋势和季节性。

—— 第 215 页，《预测：原理与实践》。

差分是通过从当前观测中减去先前观测来执行的。

difference(t) = observation(t) - observation(t-1)

1	差分(t) = 观测值(t) - 观测值(t-1)

当预测必须转换回原始尺度时，需要反转该过程。

这个过程可以通过将先前时间步的观测值加到差分值上来反转。

inverted(t) = differenced(t) + observation(t-1)

1	反转(t) = 差分(t) + 观测值(t-1)

通过这种方式，可以计算一系列差分和反转差分。

滞后差分

计算连续观测值之间的差分称为滞后 1 差分。

滞后差分可以根据特定的时间结构进行调整。

对于具有季节性成分的时间序列，滞后可能预期是季节性周期（宽度）。

差分阶数

在执行差分操作后，某些时间结构可能仍然存在，例如非线性趋势的情况。

因此，差分过程可以重复多次，直到所有时间依赖性都被去除。

执行差分操作的次数称为差分阶数。

计算差分

我们可以手动对数据集进行差分。

这涉及到开发一个新函数来创建差分数据集。该函数将遍历提供的序列，并以指定的间隔或滞后计算差分值。

下面名为 difference() 的函数实现了此过程。

# create a differenced series
def difference(dataset, interval=1):
	diff = list()
	for i in range(interval, len(dataset)):
		value = dataset[i] - dataset[i - interval]
		diff.append(value)
	return Series(diff)

# 创建差分序列

def difference(dataset, interval=1):

diff = list()

for i in range(interval, len(dataset)):

value = dataset[i] - dataset[i -interval]

diff.append(value)

return Series(diff)

我们可以看到，该函数在指定间隔后开始差分数据集，以确保可以实际计算差分值。默认的间隔或滞后值为 1。这是一个合理的默认值。

进一步的改进是能够指定执行差分操作的阶数或次数。

下面名为 inverse_difference() 的函数反转单个预测的差分操作。它要求还提供先前时间步的真实观测值。

# invert differenced forecast
def inverse_difference(last_ob, value):
	return value + last_ob

# 反转差分预测

def inverse_difference(last_ob, value):

return value + last_ob

差分去除趋势

在本节中，我们将介绍如何使用差分变换来消除趋势。

趋势通过增加水平使时间序列非平稳。这导致时间序列均值随时间变化。

下面的示例将 difference() 函数应用于一个具有线性递增趋势的人造数据集。

# create a differenced series
def difference(dataset, interval=1):
	diff = list()
	for i in range(interval, len(dataset)):
		value = dataset[i] - dataset[i - interval]
		diff.append(value)
	return diff

# invert differenced forecast
def inverse_difference(last_ob, value):
	return value + last_ob

# define a dataset with a linear trend
data = [i+1 for i in range(20)]
print(data)
# difference the dataset
diff = difference(data)
print(diff)
# invert the difference
inverted = [inverse_difference(data[i], diff[i]) for i in range(len(diff))]
print(inverted)

# 创建差分序列

def difference(dataset, interval=1):

diff = list()

for i in range(interval, len(dataset)):

value = dataset[i] - dataset[i -interval]

diff.append(value)

return diff

# 反转差分预测

def inverse_difference(last_ob, value):

return value + last_ob

# 定义一个具有线性趋势的数据集

data = [i+1 for i in range(20)]

print(data)

# 对数据集进行差分

diff = difference(data)

print(diff)

# 反转差分

inverted = [inverse_difference(data[i], diff[i]) for i in range(len(diff))]

print(inverted)

运行示例首先打印具有线性趋势的人造序列。接下来，打印差分数据集，显示每个时间步增加一个单位。此序列的长度为 19 而不是 20，因为序列中第一个值的差分无法计算，因为它没有先前的值。

最后，使用原始序列中的先前值作为每次变换的引子来反转差分序列。

[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20]
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
[2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20]

[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20]

[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]

[2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20]

差分去除季节性

在本节中，我们将介绍如何使用差分变换来去除季节性。

季节性变化，或季节性，是随时间规律性重复的循环。

一年内重复的模式称为季节性变化，尽管该术语更广泛地适用于任何固定周期内重复的模式。

—— 第 6 页，《R 语言时间序列入门》。

季节性有多种类型。一些明显的例子包括：一天中的时间、每日、每周、每月、每年等。因此，识别时间序列问题中是否存在季节性成分是主观的。

确定是否存在季节性方面的最简单方法是绘制和查看您的数据，可能以不同的尺度并添加趋势线。

下面的示例将 difference() 函数应用于一个人造季节性数据集。该数据集包括两个周期，每个周期为 360 个单位。

from math import sin
from math import radians
from matplotlib import pyplot

# create a differenced series
def difference(dataset, interval=1):
	diff = list()
	for i in range(interval, len(dataset)):
		value = dataset[i] - dataset[i - interval]
		diff.append(value)
	return diff

# invert differenced forecast
def inverse_difference(last_ob, value):
	return value + last_ob

# define a dataset with seasonality
data = [sin(radians(i)) for i in range(360)] + [sin(radians(i)) for i in range(360)]
pyplot.plot(data)
pyplot.show()
# difference the dataset
diff = difference(data, 360)
pyplot.plot(diff)
pyplot.show()
# invert the difference
inverted = [inverse_difference(data[i], diff[i]) for i in range(len(diff))]
pyplot.plot(inverted)
pyplot.show()

from math import sin

from math import radians

from matplotlib import pyplot

# 创建差分序列

def difference(dataset, interval=1):

diff = list()

for i in range(interval, len(dataset)):

value = dataset[i] - dataset[i -interval]

diff.append(value)

return diff

# 反转差分预测

def inverse_difference(last_ob, value):

return value + last_ob

# 定义一个具有季节性的数据集

data = [sin(radians(i)) for i in range(360)] + [sin(radians(i)) for i in range(360)]

pyplot.plot(data)

pyplot.show()

# 对数据集进行差分

diff = difference(data, 360)

pyplot.plot(diff)

pyplot.show()

# 反转差分

inverted = [inverse_difference(data[i], diff[i]) for i in range(len(diff))]

pyplot.plot(inverted)

pyplot.show()

运行示例首先创建并绘制了 360 个时间步序列的两个周期数据集。

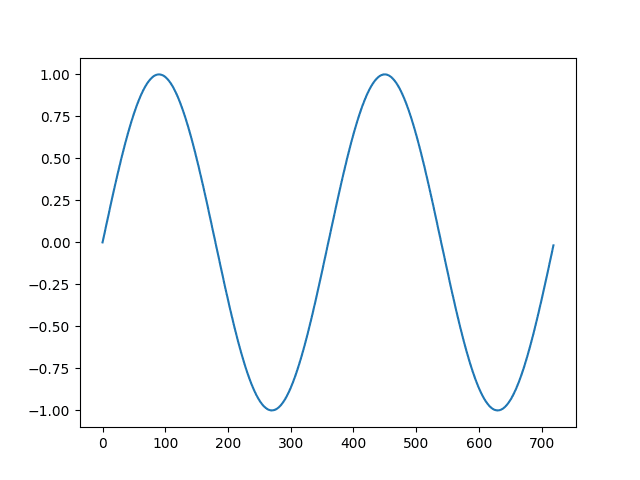
Line plot of a contrived sesonal dataset

人造季节性数据集的折线图

接下来，应用差分变换并绘制结果。该图显示了 360 个零值，所有季节性信号均已去除。

在上面的去趋势示例中，差分以滞后 1 应用，这意味着第一个值被牺牲。这里使用整个周期进行差分，即 360 个时间步。结果是整个第一个周期被牺牲，以便对第二个周期进行差分。

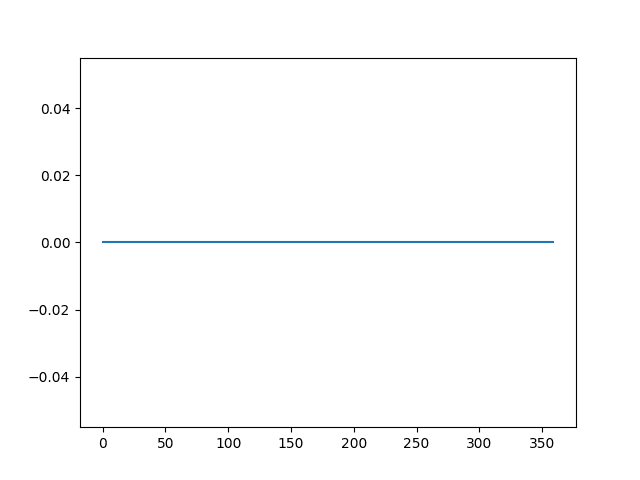
Line plot of the differenced seasonal dataset

差分季节性数据集的折线图

最后，反转变换，显示第二个周期并恢复季节性。

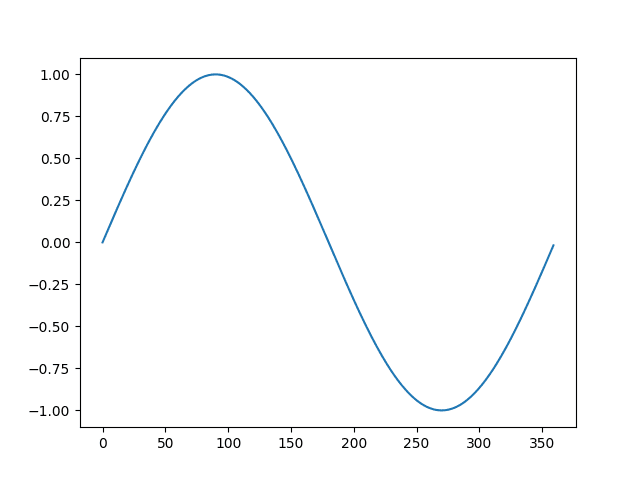
Line plot of the differenced dataset with the inverted difference transform

差分数据集与反向差分变换的折线图

进一步阅读

总结

在本教程中，您了解了平稳和非平稳时间序列之间的区别，以及如何使用 Python 中的差分变换去除趋势和季节性。

具体来说，你学到了：

平稳时间序列和非平稳时间序列之间的对比，以及如何通过差分变换使时间序列平稳。
如何应用差分变换从序列中去除线性趋势。
如何应用差分变换从序列中去除季节性信号。

您对使时间序列平稳有任何疑问吗？
在评论中提出您的问题，我将尽力回答。

关于此主题的更多信息

如何在 Python 中缩放长短期记忆网络的数据

如何在 Python 中对序列数据进行独热编码