
重新审视 k-Means:使其更好工作的 3 种方法
图片作者 | ChatGPT
引言
k-Means 算法是无监督机器学习的基石,以其简单性和在将数据划分为预定数量的簇方面的效率而闻名。其直接的方法——将数据点分配给最近的质心,然后根据分配点集的平均值更新质心——使其成为大多数数据科学家学习的第一个算法之一。它是一个主力,能够为数据集的底层结构提供快速而有价值的见解。
然而,这种简洁性也带来了一系列限制。标准的 k-Means 在处理现实世界数据的复杂性时常常会遇到困难。其性能可能对质心的初始位置敏感,需要预先指定簇的数量,并且它从根本上假设簇是球形且大小均匀的。这些假设在实际应用中很少成立,导致结果不理想甚至产生误导。
幸运的是,在 k-Means 被依赖的许多年里,数据科学界已经开发了多种巧妙的修改和扩展来解决这些不足之处。这些曾经的“技巧”,如今已成为核心的扩展,增强了 k-Means 的鲁棒性和适用性,将其从一个简单的教科书算法转变为一个实用的数据分析工具。
本教程将探讨三种在实际应用中使 k-Means 更好地工作的最有效技术,具体来说是:
- 使用 k-means++ 进行更智能的质心初始化
- 利用轮廓系数(silhouette score)找到最佳簇数量
- 应用核技巧(kernel trick)来处理非球形数据
让我们开始吧。
1. 使用 k-means++ 进行更智能的质心初始化
标准 k-Means 算法最大的弱点之一是它依赖于随机质心初始化。质心初始位置不佳会导致多种问题,包括收敛到次优的聚类解决方案,以及需要更多迭代才能收敛,这会增加计算时间。想象一下,所有初始质心都随机放置在一个密集的数据区域内——算法可能很难正确识别出位于更远处的不同簇。这种敏感性意味着对同一数据运行相同的 k-Means 算法每次都可能产生不同的结果,使得该过程的可靠性降低。
引入 k-means++ 算法是为了克服这个问题。k-means++ 不是 完全 随机放置,而是使用一种更智能、仍然是概率性的方法来播种初始质心。该过程首先 从数据点中 随机选择第一个质心。然后,对于每个后续的质心,它以 与其最近的现有质心成比例的概率 选择一个数据点。这种程序会固有地偏向那些距离已选中心更远的点,从而实现更分散、更具策略性的初始放置。这种方法增加了找到更好的最终聚类解决方案的可能性,并通常减少了收敛所需的迭代次数。
在实践中实现这一点非常简单,因为大多数现代机器学习库——包括 Scikit-learn——都已将 k-means++ 集成作为默认的初始化方法。只需指定 init='k-means++',您就可以利用这些方法,而无需进行复杂的编码。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
from sklearn.cluster import KMeans from sklearn.datasets import make_blobs # 生成示例数据 X, y = make_blobs(n_samples=10000, n_features=10, centers=5, cluster_std=2.0, random_state=42) # 使用 k-means++ 初始化进行标准 k-Means kmeans_plus = KMeans(n_clusters=5, init='k-means++', n_init=1, random_state=42) kmeans_plus.fit(X) # 作为比较,使用随机初始化的标准 k-Means kmeans_random = KMeans(n_clusters=5, init='random', n_init=1, random_state=42) kmeans_random.fit(X) print(f"k-means++ 惯性: {kmeans_plus.inertia_}") print(f"随机初始化惯性: {kmeans_random.inertia_}") |
输出
|
1 2 |
k-means++ 惯性: 400582.2443257831 随机 初始化 惯性: 664535.6265023422 |
如惯性(数据点到其质心的平方距离之和)的差异所示,在此案例中,k-means++ 的性能明显优于随机初始化。
2. 使用轮廓系数(Silhouette Score)找到最佳簇数量
k-Means 的一个明显限制性挑战是要求在运行算法之前指定簇的数量 k。在许多现实场景中,最佳簇数量是未知的。选择不正确的 k 可能导致数据被过度分割成无意义的微簇,或者被过度分割,将不同的模式组合在一起。虽然存在帮助确定最佳簇数量的方法,如“肘部法则”(elbow method),但它们可能模棱两可且难以解释,尤其是在方差的视觉图中没有明显的“肘部”时。
一种更鲁棒、更量化的方法是使用 轮廓系数。该指标通过衡量簇的分离程度来评估给定聚类解决方案的质量。对于每个数据点,轮廓系数是根据两个值计算的:
- 内聚性(cohesion)——与同一簇中其他点的平均距离
- 分离性(separation)——与最近邻簇中点的平均距离
本质上,我们衡量数据点与其自身簇中的其他数据点的相似程度,以及它们与其它簇中数据点的差异程度。直观地说,这正是成功的 k-Means 聚类解决方案应该最大化的。
这些分数范围从 -1 到 +1,其中 高值 表示该点与其自身的簇匹配良好,而与邻近簇匹配不佳。
为了找到最佳的 k,您可以对一系列不同的 k 值运行 k-Means 算法,并计算每个值的平均轮廓系数。产生最高平均分数的 k 值通常被认为是最佳选择。这种方法提供了一种更具数据驱动性的方式来确定簇的数量,超越了简单的启发式方法,并实现了更自信的选择。
让我们看看使用 Scikit-learn 计算 2 到 10 的 k 值范围内的轮廓系数的结果,确定哪个值是最佳的,并绘制结果以与这些结果进行比较。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
from sklearn.cluster import KMeans from sklearn.metrics import silhouette_score from sklearn.datasets import make_blobs import matplotlib.pyplot as plt # 生成示例数据 X, y = make_blobs(n_samples=10000, n_features=10, centers=5, cluster_std=2.0, random_state=42) # 使用轮廓系数确定最佳 k(从 2 到 10) silhouette_scores = [] k_values = range(2, 11) for k in k_values: kmeans = KMeans(n_clusters=k, init='k-means++', n_init=10, random_state=42) kmeans.fit(X) score = silhouette_score(X, kmeans.labels_) silhouette_scores.append(score) print(f"对于 k = {k},轮廓系数为 {score:.4f}") # 查找最佳 k 和最佳分数 best_score = max(silhouette_scores) optimal_k = k_values[silhouette_scores.index(best_score)] # 输出最终结果 print(f"\n最佳簇数量 (k) 为: {optimal_k}") print(f"这是根据最高轮廓系数确定的: {best_score:.4f}") # 可视化结果 plt.figure(figsize=(10, 6)) plt.plot(k_values, silhouette_scores, marker='o') plt.title('不同簇数量的轮廓系数') plt.xlabel('簇数量 (k)') plt.ylabel('轮廓系数') plt.xticks(k_values) plt.grid(True) plt.show() |
输出
|
1 2 3 4 5 6 7 8 9 10 11 12 |
对于 k = 2, 轮廓系数为 0.4831 对于 k = 3, 轮廓系数为 0.4658 对于 k = 4, 轮廓系数为 0.5364 对于 k = 5, 轮廓系数为 0.5508 对于 k = 6, 轮廓系数为 0.4464 对于 k = 7, 轮廓系数为 0.3545 对于 k = 8, 轮廓系数为 0.2534 对于 k = 9, 轮廓系数为 0.1606 对于 k = 10, 轮廓系数为 0.0695 最佳簇数量 (k) 为: 5 这是 根据最高轮廓系数确定的: 0.5508 |
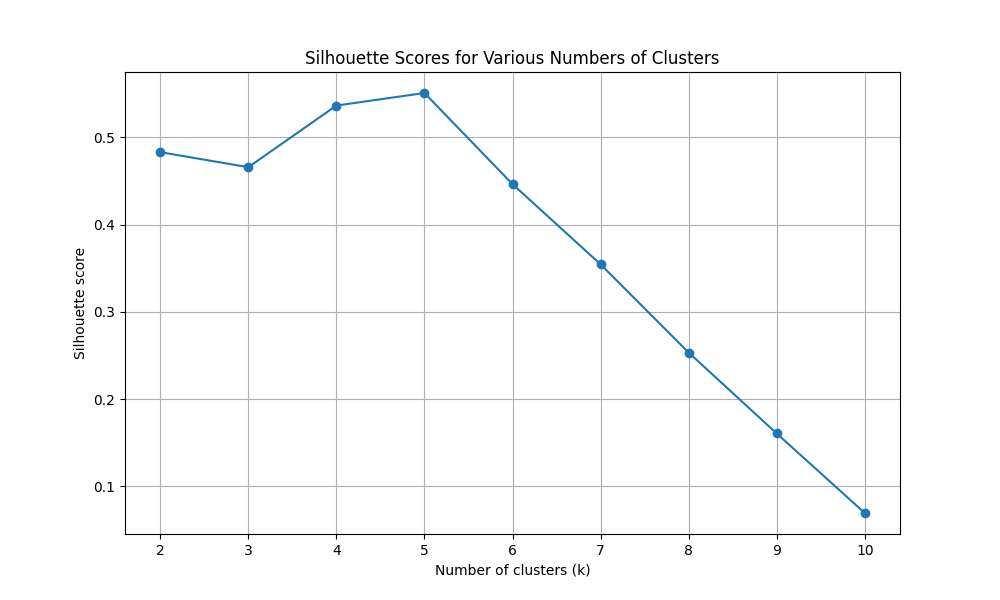
图 1:不同簇数量的轮廓系数(k 值从 2 到 10)
我们可以看到,5 是最佳的 k 值,轮廓系数为 0.5508。
3. 使用核 k-Means 处理非球形簇
k-Means 最令人沮丧和不切实际的限制可能是它假设簇是 凸且各向同性 的,这意味着它们大致是球形的并且大小相似。这是因为 k-Means 根据到中心点的距离来定义簇,这本质上会创建球状边界。当面对包含复杂、细长或非线性形状的现实世界数据时,标准的 k-Means 无法正确识别这些模式。例如,它将无法分离两个同心圆的数据点,因为它可能会用一条直线将它们分开。
为了解决这个问题,我们可以采用 核技巧,这是支持向量机工作原理中的一个核心概念。核 k-Means 的工作原理是通过隐式地将数据投影到一个更高维度的空间,在这个空间中,簇可能变得线性可分或更接近球形。这是通过使用 核函数(如径向基函数 RBF)来实现的,它可以在这个更高维度的空间中计算数据点之间的相似性,而无需显式计算它们的新坐标。通过在转换后的特征空间中进行操作,核 k-Means 可以识别出具有复杂、非球形形状的簇,这是标准算法无法检测到的。
虽然 Scikit-learn 没有直接的 KernelKMeans 实现,但其 SpectralClustering 算法提供了一种强大的替代方案,可以有效地实现类似的结果。谱聚类(Spectral clustering)使用数据的连通性来形成簇,并且在寻找非凸簇方面特别有效。它可以被视为一种核 k-Means,并且是实现此目的的绝佳工具。让我们来看看。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
from sklearn.cluster import KMeans, SpectralClustering from sklearn.datasets import make_moons import matplotlib.pyplot as plt # 生成非球形数据 X, y = make_moons(n_samples=500, noise=0.05, random_state=42) # 可视化非球形数据 plt.figure(figsize=(8, 6)) plt.scatter(X[:, 0], X[:, 1], color='blue', s=15) # 添加标题和标签以示清晰 plt.title('示例非球形数据') plt.xlabel('特征 1') plt.ylabel('特征 2') plt.grid(True, linestyle='--', alpha=0.6) plt.show() # 应用标准 k-Means kmeans = KMeans(n_clusters=2, n_init=10, random_state=42) kmeans_labels = kmeans.fit_predict(X) # 应用谱聚类(作为核 k-Means 的替代方案) spectral = SpectralClustering(n_clusters=2, affinity='nearest_neighbors', random_state=42) spectral_labels = spectral.fit_predict(X) # 可视化结果 fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 6)) ax1.scatter(X[:, 0], X[:, 1], c=kmeans_labels, cmap='viridis', s=50) ax1.set_title('标准 K-Means 聚类') ax1.set_xlabel('特征 1') ax1.set_ylabel('特征 2') ax2.scatter(X[:, 0], X[:, 1], c=spectral_labels, cmap='viridis', s=50) ax2.set_title('谱聚类') ax2.set_xlabel('特征 1') ax2.set_ylabel('特征 2') plt.suptitle('非球形数据上的聚类比较') plt.show() |
输出
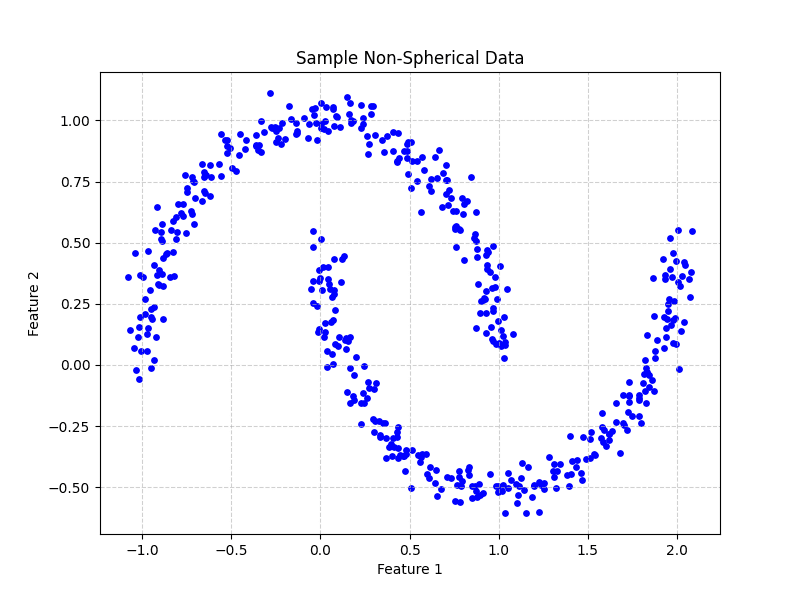
图 2:示例非球形数据
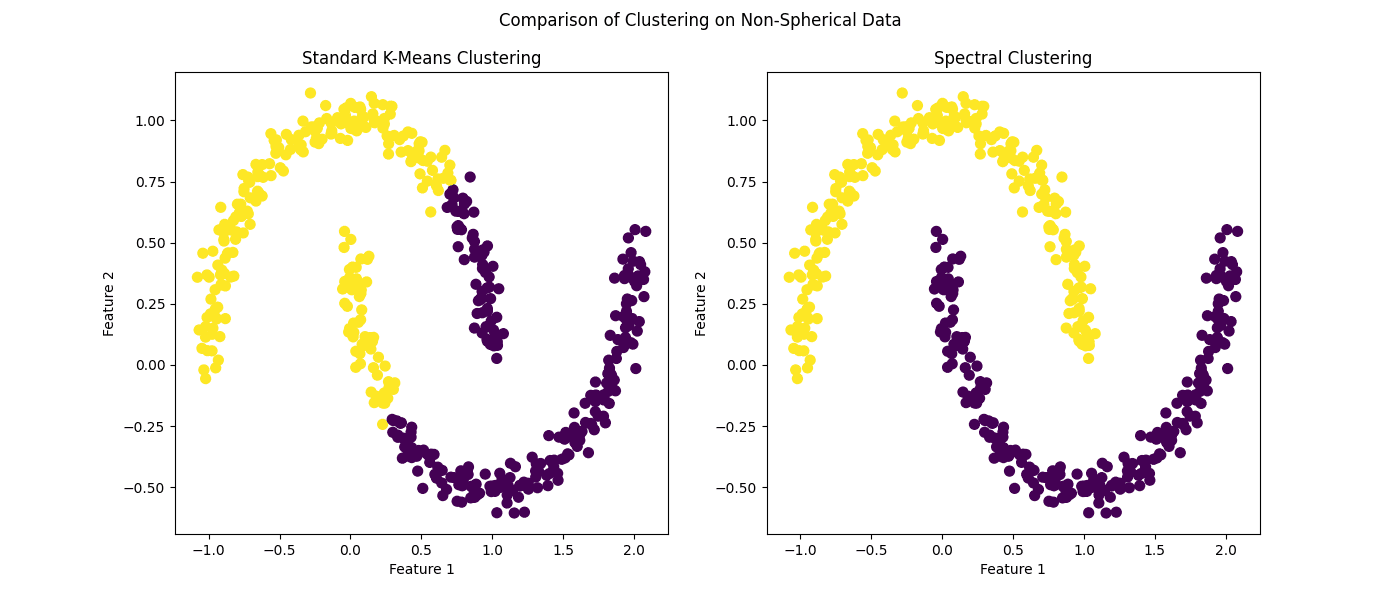
图 3:非球形数据上的聚类比较
几乎不需要指出的是,谱聚类——作为核 k-Means 的替代方案——在此场景下优于其标准对应物。
总结
虽然 k-Means 算法通常被介绍为一种基础聚类技术,但它的用途超出了入门示例。通过结合一些巧妙的方法,我们可以克服其最主要的限制,并使其适应现实世界数据的混乱、复杂性。这些增强表明,即使是基础算法,只要经过适当的修改,仍然可以保持高度相关性和强大。
- 使用 k-means++ 进行初始化可以提供更鲁棒的起点,从而获得更好、更一致的结果。
- 轮廓系数提供了一种量化方法来确定最佳簇数量,消除了算法关键参数之一的猜测。
- 通过诸如谱聚类之类的技术利用核方法,可以使 k-Means 打破其球形簇的假设,并识别数据中复杂的模式。
不要过快地否定 k-means;通过应用这些实用技术,您可以释放其全部潜力,并从数据中获得更深入、更准确的见解。




暂无评论。