当数值输入变量被缩放到标准范围时,许多机器学习算法表现更好。
这包括使用输入加权和的算法,如线性回归,以及使用距离度量的算法,如 k 近邻。
标准化是一种流行的缩放技术,它通过从值中减去均值并除以标准差来完成,将输入变量的概率分布转换为标准高斯分布(均值为零,方差为一)。如果输入变量包含异常值,标准化可能会变得偏差过大或有偏。
为了克服这个问题,在标准化数值输入变量时可以使用中位数和四分位距,这通常被称为稳健缩放。
在本教程中,您将了解如何使用稳健缩放器变换来标准化分类和回归的数值输入变量。
完成本教程后,您将了解:
- 许多机器学习算法在数值输入变量被缩放时会表现得更好,或者更喜欢被缩放。
- 可以使用基于百分位数的稳健缩放技术来缩放包含异常值的数值输入变量。
- 如何使用 RobustScaler 通过中位数和四分位距缩放数值输入变量。
快速开始您的项目,阅读我的新书 机器学习数据准备,其中包含分步教程和所有示例的Python源代码文件。
让我们开始吧。

如何为机器学习使用稳健缩放器变换
照片作者:Ray in Manila,保留部分权利。
教程概述
本教程分为五个部分;它们是:
- 数据缩放
- 稳健缩放器变换
- 声纳数据集
- IQR 稳健缩放器变换
- 探索稳健缩放器范围
稳健缩放数据
在拟合机器学习模型之前,通常需要对数据进行缩放。
这是因为数据通常包含许多不同的输入变量或特征(列),并且每一列可能有不同的值范围或测量单位,例如英尺、英里、公斤、美元等。
如果存在一些输入变量的值相对于其他输入变量非常大,这些大值可能会主导或扭曲某些机器学习算法。结果是算法将大部分注意力放在大值上,而忽略了值较小的变量。
这包括使用加权输入和的算法,如线性回归、逻辑回归和人工神经网络,以及使用示例之间距离度量的算法,如 K 近邻和支持向量机。
因此,将输入变量缩放到通用范围作为数据准备技术,在拟合模型之前是正常的。
一种数据缩放方法包括计算每个变量的均值和标准差,并使用这些值将值缩放到均值为零、标准差为一,即所谓的“标准正态”概率分布。此过程称为标准化,当输入变量具有高斯概率分布时最有用。
标准化是通过减去均值并除以标准差来计算的。
- 值 = (值 – 均值) / 标准差
有时输入变量可能包含异常值。这些是分布边缘的值,其发生概率可能很低,但由于某种原因却被过度表示。异常值会扭曲概率分布,并使使用标准化的数据缩放变得困难,因为计算出的均值和标准差会因异常值的存在而发生偏差。
在存在异常值的情况下标准化输入变量的一种方法是从均值和标准差的计算中忽略异常值,然后使用计算出的值来缩放变量。
这称为稳健标准化或稳健数据缩放。
这可以通过计算中位数(第 50 百分位数)以及第 25 和第 75 百分位数来实现。然后,每个变量的值减去其各自的中位数,并除以四分位距(IQR),即第 75 和第 25 百分位数之间的差值。
- 值 = (值 – 中位数) / (p75 – p25)
生成的变量的均值和中位数为零,标准差为 1,但不受异常值影响,异常值仍然保留与其他值的相对关系。
想开始学习数据准备吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
稳健缩放器变换
通过 scikit-learn Python 机器学习库中的 RobustScaler 类 可用稳健缩放器变换。
“with_centering” 参数控制值是否居中到零(减去中位数),默认为 True。
“with_scaling” 参数控制值是否缩放到 IQR(标准差设为一)或不缩放,默认为 True。
有趣的是,缩放范围的定义可以通过“quantile_range”参数指定。它接受一个介于 0 和 100 之间的整数元组,默认值为 IQR 的百分位数,具体为 (25, 75)。更改此值将改变异常值的定义和缩放的范围。
我们将更详细地了解如何在真实数据集上使用稳健缩放器变换。
首先,让我们介绍一个真实数据集。
声纳数据集
声纳数据集是用于二元分类的标准机器学习数据集。
它涉及 60 个实值输入和一个二类目标变量。数据集中有 208 个示例,并且类别相当平衡。
基线分类算法在使用重复分层 10 折交叉验证时,分类准确率约为 53.4%。在此数据集上的最佳性能(使用重复分层 10 折交叉验证)约为 88%。
数据集描述了岩石或模拟地雷的雷达回波。
您可以从这里了解更多关于数据集的信息
无需下载数据集;我们将从我们的示例中自动下载它。
首先,让我们加载并总结数据集。完整的示例列在下面。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# 加载并总结声纳数据集 from pandas import read_csv from pandas.plotting import scatter_matrix from matplotlib import pyplot # 加载数据集 url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/sonar.csv" dataset = read_csv(url, header=None) # 总结数据集的形状 print(dataset.shape) # 总结每个变量 print(dataset.describe()) # 变量的直方图 dataset.hist() pyplot.show() |
运行示例首先总结加载数据集的形状。
这证实了 60 个输入变量、一个输出变量和 208 行数据。
提供了输入变量的统计摘要,显示值是数值,大约在 0 到 1 之间。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
(208, 61) 0 1 2 ... 57 58 59 count 208.000000 208.000000 208.000000 ... 208.000000 208.000000 208.000000 mean 0.029164 0.038437 0.043832 ... 0.007949 0.007941 0.006507 std 0.022991 0.032960 0.038428 ... 0.006470 0.006181 0.005031 min 0.001500 0.000600 0.001500 ... 0.000300 0.000100 0.000600 25% 0.013350 0.016450 0.018950 ... 0.003600 0.003675 0.003100 50% 0.022800 0.030800 0.034300 ... 0.005800 0.006400 0.005300 75% 0.035550 0.047950 0.057950 ... 0.010350 0.010325 0.008525 max 0.137100 0.233900 0.305900 ... 0.044000 0.036400 0.043900 [8 rows x 60 columns] |
最后,为每个输入变量创建了一个直方图。
如果我们忽略图表的杂乱,只关注直方图本身,我们可以看到许多变量具有偏斜分布。
该数据集为使用稳健缩放器变换来标准化数据(在存在偏斜分布和异常值的情况下)提供了一个很好的候选。
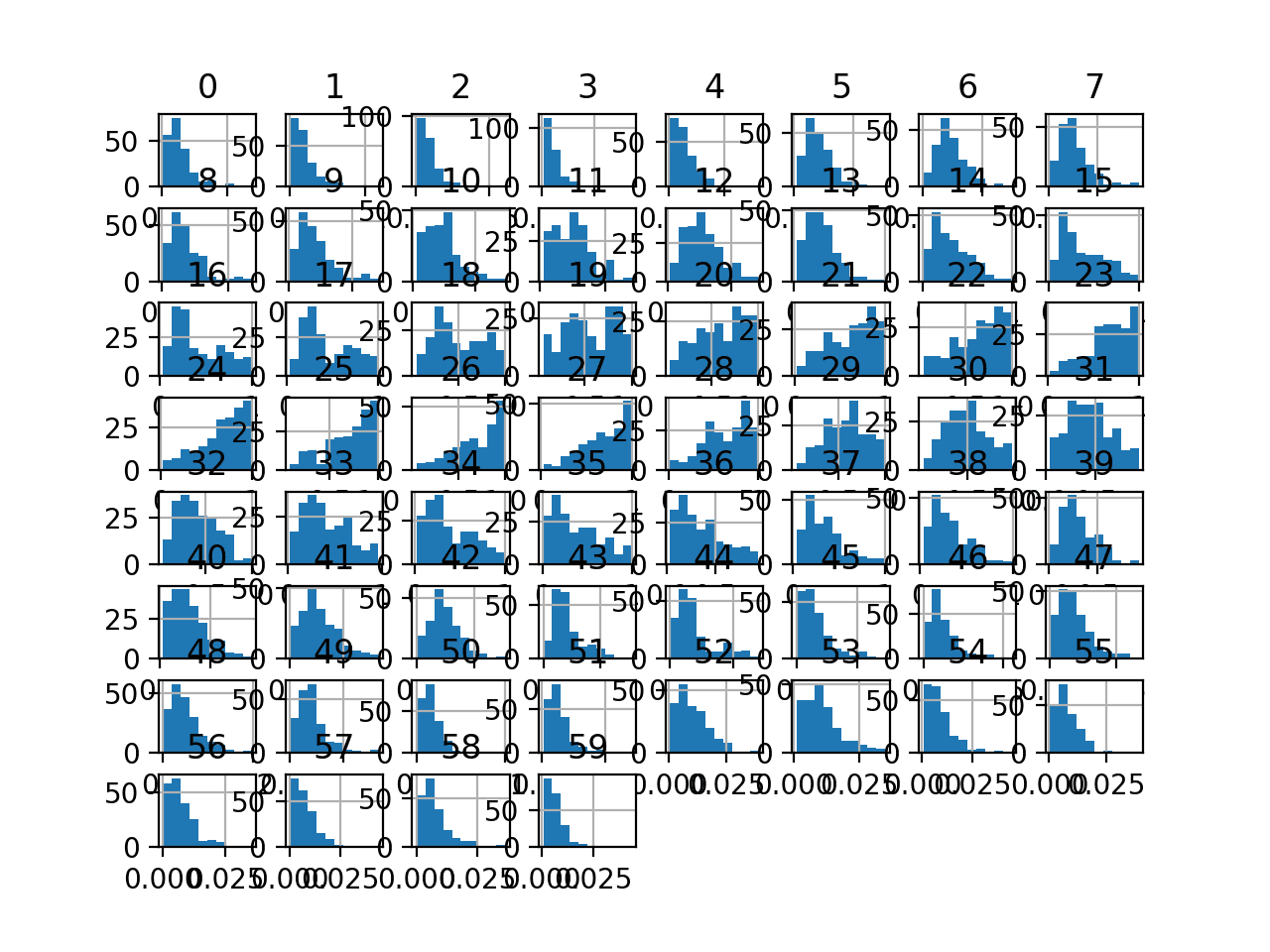
声纳二元分类数据集输入变量的直方图图
接下来,让我们在原始数据集上拟合和评估一个机器学习模型。
我们将使用具有默认超参数的 K 近邻算法,并使用重复分层 K 折交叉验证对其进行评估。完整的示例列示如下。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
# 在原始声纳数据集上评估 knn from numpy import mean from numpy import std from pandas import read_csv from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.neighbors import KNeighborsClassifier from sklearn.preprocessing import LabelEncoder from matplotlib import pyplot # 加载数据集 url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/sonar.csv" dataset = read_csv(url, header=None) data = dataset.values # 分割为输入和输出列 X, y = data[:, :-1], data[:, -1] # 确保输入是浮点数,输出是整数标签 X = X.astype('float32') y = LabelEncoder().fit_transform(y.astype('str')) # 定义和配置模型 model = KNeighborsClassifier() # 评估模型 cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) n_scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1, error_score='raise') # 报告模型性能 print('Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores))) |
运行示例评估 KNN 模型在原始声纳数据集上的性能。
我们可以看到,该模型实现了大约 79.7% 的平均分类准确率,这表明它具有技能(优于 53.4%),并且接近良好性能(88%)。
|
1 |
准确率:0.797 (0.073) |
接下来,让我们探索一下对数据集进行稳健缩放变换。
IQR 稳健缩放器变换
我们可以直接将稳健缩放器应用于 Sonar 数据集。
我们将使用默认配置并按 IQR 缩放值。首先,使用默认超参数定义一个 RobustScaler 实例。定义后,我们可以调用 fit_transform() 函数并将其应用于我们的数据集,以创建数据集的量化变换版本。
|
1 2 3 4 |
... # 对数据集执行稳健缩放变换 trans = RobustScaler() data = trans.fit_transform(data) |
让我们在声纳数据集上尝试一下。
Sonar 数据集的稳健缩放变换的完整示例以及结果直方图如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
# 可视化 Sonar 数据集的稳健缩放变换 from pandas import read_csv from pandas import DataFrame from pandas.plotting import scatter_matrix from sklearn.preprocessing import RobustScaler from matplotlib import pyplot # 加载数据集 url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/sonar.csv" dataset = read_csv(url, header=None) # 仅检索数字输入值 data = dataset.values[:, :-1] # 对数据集执行稳健缩放变换 trans = RobustScaler() data = trans.fit_transform(data) # 将数组转换回数据框 dataset = DataFrame(data) # 总结 print(dataset.describe()) # 变量的直方图 dataset.hist() pyplot.show() |
运行示例首先报告每个输入变量的摘要。
我们可以看到分布已被调整。中位数现在为零,标准差现在接近 1.0。
|
1 2 3 4 5 6 7 8 9 10 11 |
0 1 ... 58 59 count 208.000000 208.000000 ... 2.080000e+02 208.000000 mean 0.286664 0.242430 ... 2.317814e-01 0.222527 std 1.035627 1.046347 ... 9.295312e-01 0.927381 min -0.959459 -0.958730 ... -9.473684e-01 -0.866359 25% -0.425676 -0.455556 ... -4.097744e-01 -0.405530 50% 0.000000 0.000000 ... 6.591949e-17 0.000000 75% 0.574324 0.544444 ... 5.902256e-01 0.594470 max 5.148649 6.447619 ... 4.511278e+00 7.115207 [8 rows x 60 columns] |
变量的直方图被绘制出来,尽管分布看起来与前一节中看到的原始分布差别不大。
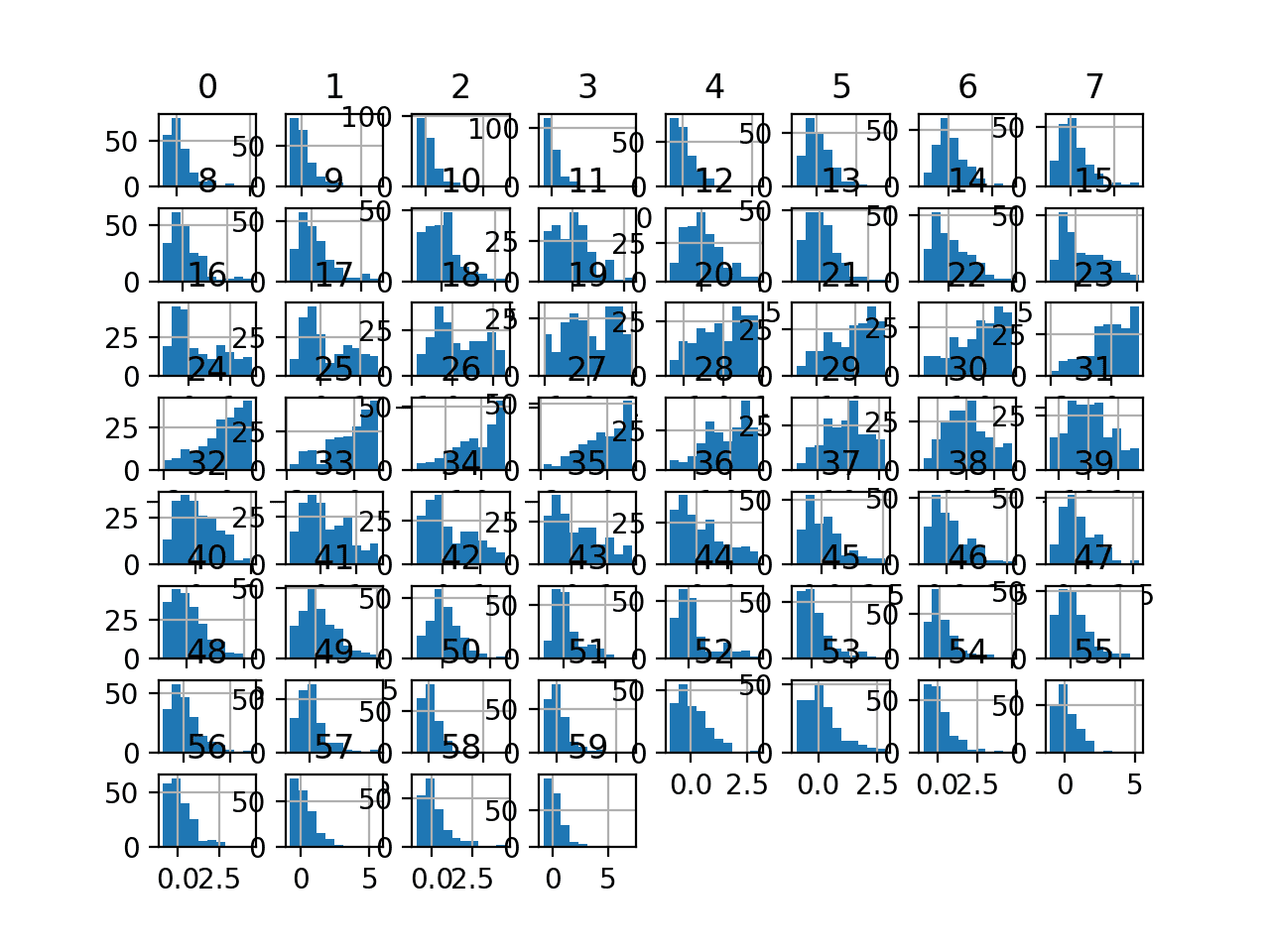
Sonar 数据集稳健缩放变换后的输入变量直方图
接下来,让我们评估与上一节相同的 KNN 模型,但在本例中是针对数据集的稳健缩放变换。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
# 使用稳健缩放器变换评估 Sonar 数据集上的 KNN from numpy import mean from numpy import std from pandas import read_csv from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.neighbors import KNeighborsClassifier from sklearn.preprocessing import LabelEncoder from sklearn.preprocessing import RobustScaler from sklearn.pipeline import Pipeline from matplotlib import pyplot # 加载数据集 url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/sonar.csv" dataset = read_csv(url, header=None) data = dataset.values # 分割为输入和输出列 X, y = data[:, :-1], data[:, -1] # 确保输入是浮点数,输出是整数标签 X = X.astype('float32') y = LabelEncoder().fit_transform(y.astype('str')) # 定义管道 trans = RobustScaler(with_centering=False, with_scaling=True) model = KNeighborsClassifier() pipeline = Pipeline(steps=[('t', trans), ('m', model)]) # 评估管道 cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) n_scores = cross_val_score(pipeline, X, y, scoring='accuracy', cv=cv, n_jobs=-1, error_score='raise') # 报告管道性能 print('Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores))) |
注意:您的结果可能因算法或评估程序的随机性,或数值精度的差异而异。请考虑运行示例几次并比较平均结果。
运行该示例,我们可以看到稳健缩放变换使性能从没有变换时的 79.7% 准确率提升到有变换时的约 81.9%。
|
1 |
Accuracy: 0.819 (0.076) |
接下来,让我们探讨不同缩放范围的影响。
探索稳健缩放器范围
用于缩放每个变量的范围默认选择为 IQR,它由第 25 和第 75 百分位数界定。
这通过“quantile_range”参数指定为一个元组。
可以指定其他值,并且可能会提高模型的性能,例如更宽的范围,允许更少的值被视为异常值,或者更窄的范围,允许更多值被视为异常值。
下面的示例探索了从第 1 个到第 99 个百分位数到第 30 个到第 70 个百分位数的不同范围定义的效果。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 |
# 探索稳健缩放变换的缩放范围 from numpy import mean from numpy import std from pandas import read_csv from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.neighbors import KNeighborsClassifier from sklearn.preprocessing import RobustScaler from sklearn.preprocessing import LabelEncoder from sklearn.pipeline import Pipeline from matplotlib import pyplot # 获取数据集 定义 获取_数据集(): # 加载数据集 url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/sonar.csv" dataset = read_csv(url, header=None) data = dataset.values # 分离输入和输出列 X, y = data[:, :-1], data[:, -1] # 确保输入为浮点数,输出为整数标签 X = X.astype('float32') y = LabelEncoder().fit_transform(y.astype('str')) 返回 X, y # 获取要评估的模型列表 定义 获取_模型(): models = dict() for value in [1, 5, 10, 15, 20, 25, 30]: # 定义管道 trans = RobustScaler(quantile_range=(value, 100-value)) model = KNeighborsClassifier() models[str(value)] = Pipeline(steps=[('t', trans), ('m', model)]) 返回 模型 # 使用交叉验证评估给定模型 def evaluate_model(model, X, y): cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1, error_score='raise') 返回 分数 # 定义数据集 X, y = get_dataset() # 获取要评估的模型 模型 = 获取_模型() # 评估模型并存储结果 results, names = list(), list() for name, model in models.items(): scores = evaluate_model(model, X, y) results.append(scores) names.append(name) print('>%s %.3f (%.3f)' % (name, mean(scores), std(scores))) # 绘制模型性能以供比较 pyplot.boxplot(results, labels=names, showmeans=True) pyplot.show() |
运行示例报告了每个值定义的 IQR 范围的平均分类准确率。
注意:您的结果可能因算法或评估程序的随机性,或数值精度的差异而异。请考虑运行示例几次并比较平均结果。
我们可以看到,默认的第 25 至第 75 百分位数达到了最佳结果,尽管 20-80 和 30-70 的值也取得了非常相似的结果。
|
1 2 3 4 5 6 7 |
>1 0.818 (0.069) >5 0.813 (0.085) >10 0.812 (0.076) >15 0.811 (0.081) >20 0.811 (0.080) >25 0.819 (0.076) >30 0.816 (0.072) |
创建箱线图来总结每个 IQR 范围的分类准确率得分。
我们可以看到,在第 25-75 和第 30-70 百分位数的较大范围内,分布和平均准确率有显著差异。
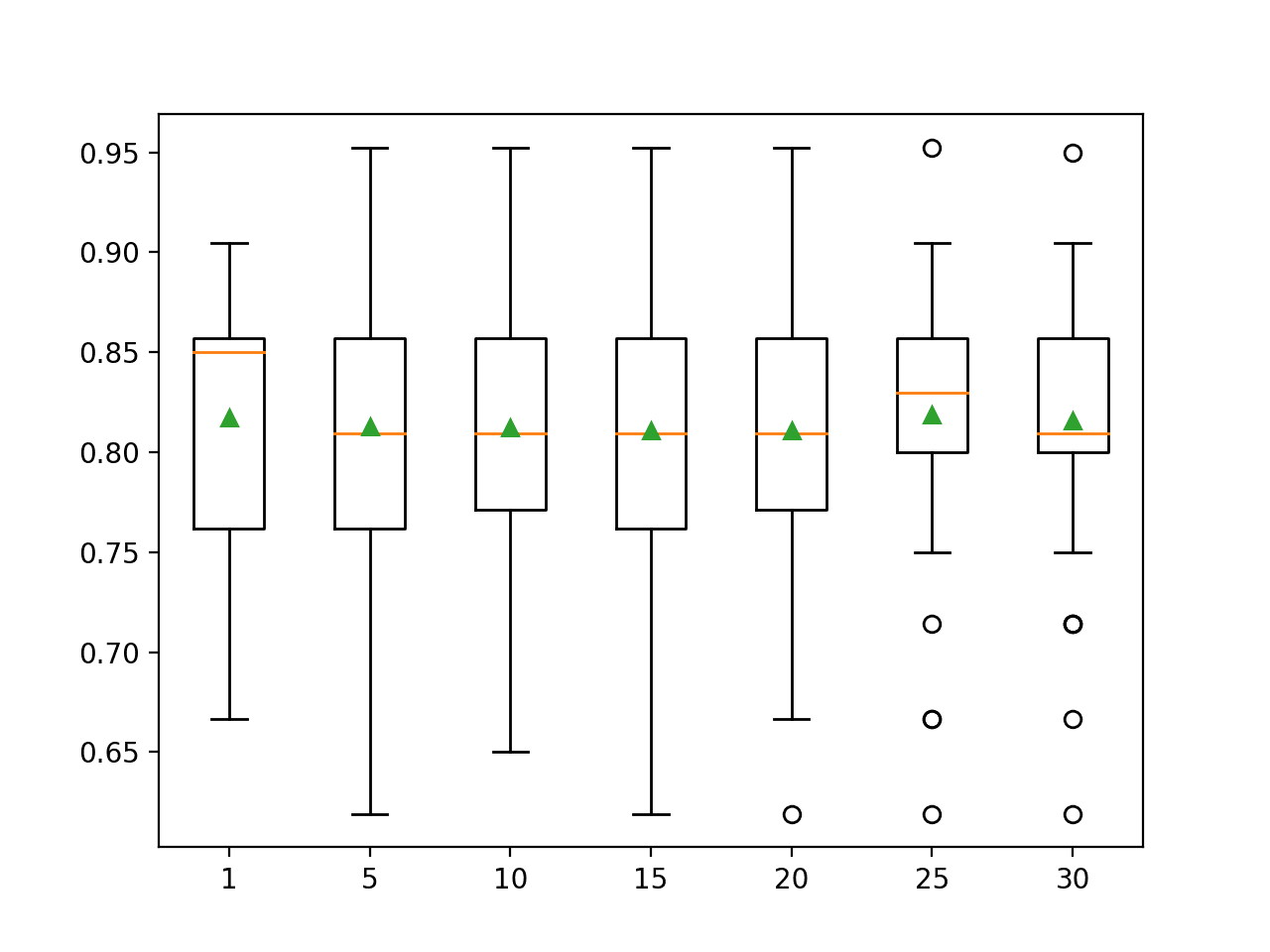
Sonar 数据集上 KNN 分类准确率与稳健缩放器 IQR 范围的箱线图
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
教程
API
文章
总结
在本教程中,您了解了如何使用稳健缩放器变换来标准化分类和回归的数值输入变量。
具体来说,你学到了:
- 许多机器学习算法在数值输入变量被缩放时会表现得更好,或者更喜欢被缩放。
- 可以使用基于百分位数的稳健缩放技术来缩放包含异常值的数值输入变量。
- 如何使用 RobustScaler 通过中位数和四分位距缩放数值输入变量。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。






嗨 Jason
在分割数据之前和之后进行转换,这两者之间有什么区别吗?
谢谢*
*顺便说一句,到目前为止,我买了您 18 本电子书,而且我是月度赞助者,我鼓励大家这样做。您做得非常出色,值得充分认可和支持。
是的。
我们必须仅在训练数据集上准备数据转换,否则我们会冒险数据泄露,从而导致我们无法信任的结果。
https://machinelearning.org.cn/data-leakage-machine-learning/
这有帮助吗?
再次感谢您的支持。非常感激!
我很乐意帮忙。
好的,那么假设我已经这样进行了分割:
60% – 训练
20% – 验证
20% – 测试/留存
所以在我进行 model.fit() 时,我将使用训练和验证数据。
现在,我应该只在训练数据集上准备数据转换 .fit_transform() 吗?还是将训练和验证数据一起进行?
顺便说一句,我开始使用一个浏览器扩展来阻止干扰,以便专注于您的网站。所以请期待我提出更多问题 🙂
再次感谢您的支持。非常感激!
只训练。
你好 Jason,
我也有同样的问题。如何在不使用验证集的情况下仅转换训练集?您的意思是执行完 K 折交叉验证后再进行转换吗?
我的第二个问题是,您是否只转换输入变量,而将目标变量保持不变(编码后)?
另外,如果我想同时使用稳健缩放器和标准化器,我应该先使用稳健缩放器吗?
我的最后一个问题是关于本教程中的最终结果和箱线图。您的意思是,我们应该选择产生最高均值和最低标准差的那个(即在这种情况下,25-75 和 20-80 模型是最好的)?
Jenny 你好…你可以在转换之前简单地分离训练集和验证集。
我想如果使用 pipeline 对象,它会自动完成工作。
你好,Jason。
感谢精彩的文章。
我在这里感到困惑,你在这里将数据集拆分成训练集和测试集。
谢谢
Jon
本教程中使用 K 折交叉验证,在此处了解它
https://machinelearning.org.cn/k-fold-cross-validation/
当您使用已缩放、转换等的数据训练模型时,当模型投入生产时,您是否必须在将生产数据输入模型进行预测之前应用相同的准备工作?
是的,没错!
看这里
https://machinelearning.org.cn/how-to-save-and-load-models-and-data-preparation-in-scikit-learn-for-later-use/
谢谢。后续的文章非常有帮助。
当我们考虑50%百分位数,即均值……
使用25%和75%百分位数以及四分位距的目的是提高准确性吗?
抱歉,我没明白。您能详细说明或重新表述一下您的问题吗?
你好 Jason,
感谢这篇精彩的文章。您知道R的任何库中有类似的功能吗?
谢谢你。
我可能会,您需要搜索一下博客,抱歉。我很多年没用过R了。
精彩的文章!
您提到线性回归就是一个受特征尺度影响的例子。但是,如果一个特征的尺度比其他特征大几个数量级,那么与其关联的参数会不会因为补偿而变得很小?
是的,它会起作用,尽管输入具有相同尺度时,优化问题会更稳定/更快。
你好 Jason,
我认为鲁棒缩放的公式不是
value = (value – median) / (p75 – p25),而是
value = (value – p25) / (p75 – p25)
因为它类似于最小-最大归一化 (value = (value – min) / (max – min))。
您同意吗?如果您不同意,能否提供参考资料?
我相信它是正确的。例如,减去中心趋势,然后除以范围。
您可以在这里查看实现
https://github.com/scikit-learn/scikit-learn/blob/0fb307bf3/sklearn/preprocessing/_data.py#L1241
是的,您说得对,谢谢。
不客气。
Jason,感谢您的教程。我只是想知道您的意思是
“value = (value – median) / (p75 – p25)
生成的变量具有零均值和中位数,标准差为1,尽管不受离群值影响,并且离群值仍以与其他值的相同相对关系存在。”
一旦经过鲁棒缩放 (x-x.median())/x.iqr()?这假定 (x.mean()-x.median())/x.iqr() = 0 => x.mean() = x.median(),这不一定是真的。还是您指的是在标准化 (x-x.mean())/x.std() 之后?
这意味着缩放后的数据中位数为0。
谢谢Jason,您的博客文章和见解是无价的!
只有一个问题:一旦应用了鲁棒缩放器,数据集的中位数将为0。
但是,数据集不会在 [0 1] 或 [-1 1] 的范围内。
对吗?
这是否可以接受,还是在应用鲁棒缩放器之后,我们需要将数据集的范围重新调整到 [0 1] 或 [-1 1] 的范围内?
提前感谢您的回复。
祝您有美好的一天。
Giuseppe
您好 Giuseppe……您可能会发现以下内容很有趣
https://www.geeksforgeeks.org/standardscaler-minmaxscaler-and-robustscaler-techniques-ml/
您好 Giuseppe,
我有一个和您一样关于将范围转换为 0到1 或 -1到1 的问题。您能找到一些有用的信息吗?