本文将使用爱荷华州埃姆斯市的住房数据集,演示 Lasso、Ridge 和 ElasticNet 模型的使用。当处理可能存在多重共线性问题的数据时,这些模型尤其有价值。我们利用这些高级回归技术来展示特征缩放和超参数调整如何提高模型性能。在本篇博文中,我们将提供一个分步指南,介绍如何设置预处理流水线,使用 scikit-learn 实现每个模型,并对它们进行微调以获得最佳结果。这种全面的方法不仅有助于提高预测准确性,还能加深您对不同正则化方法如何影响模型训练和结果的理解。
通过我的书《进阶数据科学》启动您的项目。它提供了带有可运行代码的自学教程。
让我们开始吧。

迈向成功:实施和优化惩罚模型
摄影:Jeffrey F Lin。部分权利保留。
概述
这篇博文分为三部分;它们是:
- 特征缩放在惩罚性回归模型中的关键作用
- 使用埃姆斯数据集实际实现惩罚性模型
- 优化惩罚性回归模型的超参数
特征缩放在惩罚性回归模型中的关键作用
数据预处理是显著影响模型性能的关键步骤。一个重要的预处理步骤,特别是对于 Lasso、Ridge 和 ElasticNet 等惩罚性回归模型,是特征缩放。但特征缩放究竟是什么?为什么这些模型离不开它?
什么是特征缩放?
特征缩放是一种用于标准化数据中自变量或特征范围的方法。最常用的技术称为标准化,它包括重新缩放特征,使其均值都为零,标准差都为一。通过从每个特征的每个观测值中减去该特征的均值,然后除以该特征的标准差来实现此调整。
在应用惩罚性模型之前进行缩放为什么至关重要?
惩罚性回归模型向系数大小添加惩罚,这有助于减少过拟合并提高模型的泛化能力。然而,这些惩罚的有效性在很大程度上取决于输入特征的尺度。
- 统一的惩罚应用:如果不进行缩放,具有较大尺度的特征可能会不成比例地影响模型。这种不平衡可能导致模型不公平地惩罚小尺度特征,从而可能忽略它们的重要影响。
- 模型稳定性和收敛性:具有不同尺度的特征可能在模型训练期间导致数值不稳定。这种不稳定性可能导致难以收敛到最优解决方案,或者得到次优模型。
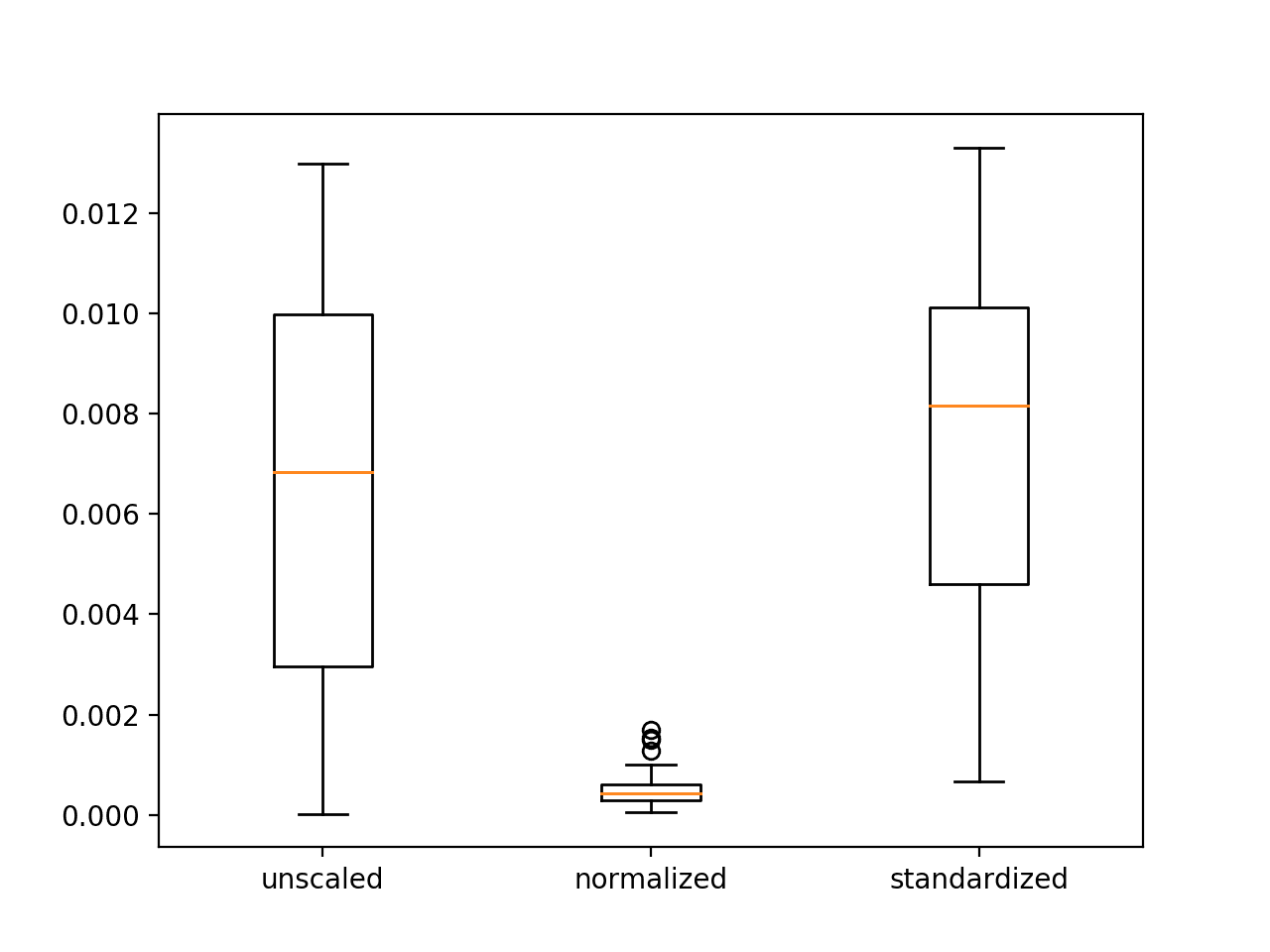
在下面的示例中,我们将演示如何对数值特征使用 StandardScaler 类来有效解决这些问题。此方法可确保我们的惩罚性模型—Lasso、Ridge 和 ElasticNet—发挥最佳性能,提供可靠且稳健的预测。
想开始学习进阶数据科学吗?
立即参加我的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
使用埃姆斯数据集实际实现惩罚性模型
在讨论了特征缩放的重要性之后,让我们通过一个实际示例来深入了解埃姆斯住房数据集。此示例演示了如何使用 scikit-learn 在 Python 中对数据进行预处理并应用惩罚性回归模型。该过程涉及为数值和分类数据设置流水线,确保工作流程健壮且可复现。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 |
# 导入必要的库 import pandas as pd from sklearn.pipeline import Pipeline from sklearn.preprocessing import StandardScaler, OneHotEncoder from sklearn.compose import ColumnTransformer from sklearn.model_selection import cross_val_score from sklearn.linear_model import Lasso, Ridge, ElasticNet # 加载数据集并删除具有缺失值的列 Ames = pd.read_csv('Ames.csv').dropna(axis=1) # 识别数值和分类特征,排除 'PID' 和 'SalePrice' numeric_features = Ames.select_dtypes(include=['int64', 'float64']).drop(columns=['PID', 'SalePrice']).columns categorical_features = Ames.select_dtypes(include=['object']).columns X = Ames[numeric_features.tolist() + categorical_features.tolist()] # 目标变量 y = Ames['SalePrice'] # 数值特征的流水线 numeric_transformer = Pipeline(steps=[ ('scaler', StandardScaler()) ]) # 分类特征的流水线 categorical_transformer = Pipeline(steps=[ ('onehot', OneHotEncoder(handle_unknown='ignore')) ]) # 数值和分类数据的组合预处理器 preprocessor = ColumnTransformer( transformers=[ ('num', numeric_transformer, numeric_features), ('cat', categorical_transformer, categorical_features) ]) # 定义带预处理器和回归器的模型流水线 pipelines = { 'Lasso': Pipeline(steps=[('preprocessor', preprocessor), ('regressor', Lasso(max_iter=20000))]), 'Ridge': Pipeline(steps=[('preprocessor', preprocessor), ('regressor', Ridge())]), 'ElasticNet': Pipeline(steps=[('preprocessor', preprocessor), ('regressor', ElasticNet())]) } # 执行交叉验证并将结果存储在字典中 cv_results = {} for name, pipeline in pipelines.items(): scores = cross_val_score(pipeline, X, y) cv_results[name] = round(scores.mean(), 4) # 输出平均交叉验证得分 print(cv_results) |
首先,我们导入必要的库并加载埃姆斯数据集,删除任何具有缺失值的列以简化初始模型。我们识别并分离数值和分类特征,排除了“PID”(每个房产的唯一标识符)和“SalePrice”(我们的目标变量)。
然后,我们为预处理构建了两个独立的流水线
- 数值特征:我们使用
StandardScaler来标准化数值特征,确保它们对模型做出相等贡献,而不会因原始尺度而产生偏差。 - 分类特征:使用
OneHotEncoder将分类变量转换为可以提供给机器学习算法的格式,处理未来数据集中可能出现的任何未知类别。
这两个流水线被合并到一个 ColumnTransformer 中。这种设置简化了代码,并将所有预处理步骤封装到一个单独的转换器对象中,该对象可以无缝集成到任何模型中。在定义了预处理之后,我们设置了三个不同的流水线,每个流水线对应一个不同的惩罚性回归模型:Lasso、Ridge 和 ElasticNet。每个流水线都集成了 ColumnTransformer 和回归器,使我们能够在代码中保持清晰性和模块化。在对我们的惩罚性回归模型应用交叉验证后,我们获得了以下得分:
|
1 |
{'Lasso': 0.8863, 'Ridge': 0.8885, 'ElasticNet': 0.8299} |
这些结果表明,虽然所有三个模型都表现得相当好,但在当前设置下,Ridge 在这三个模型中处理此数据集的效果最好。
优化惩罚性回归模型的超参数
在为埃姆斯住房数据集奠定特征缩放基础并实现惩罚性模型后,我们现在将重点放在模型开发的一个重要方面——超参数调整。此过程对于完善我们的模型并获得最佳性能至关重要。在本节中,我们将探讨如何调整超参数,特别是正则化强度(alpha)和 ElasticNet 的 L1 和 L2 惩罚之间的平衡(l1_ratio),如何影响我们模型的性能。
对于Lasso 模型,我们专注于调整 alpha 参数,该参数控制L1 惩罚的强度。L1 惩罚鼓励模型减少非零系数的数量,这可能导致更简单、更具可解释性的模型。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
#构建于上述代码块之上 # 对 Lasso 实现 GridSearchCV 以获得最佳 alpha from sklearn.model_selection import GridSearchCV # 定义 Lasso 的 alpha 值范围 alpha = list(range(1, 21, 1)) # 范围从 1 到 20,增量为 1 # 设置 Lasso 的网格搜索 lasso_grid = GridSearchCV(estimator=pipelines['Lasso'], param_grid={'regressor__alpha': alpha}, verbose=1) # 打印进度 lasso_grid.fit(X, y) # 提取 Lasso 的最佳 alpha 和最佳得分 lasso_best_alpha = lasso_grid.best_params_['regressor__alpha'] lasso_best_score = lasso_grid.best_score_ print(f"Lasso 的最佳 alpha: {lasso_best_alpha}") print(f"最佳交叉验证得分: {round(lasso_best_score, 4)}") |
在 GridSearchCV 设置中将 verbose=1 提供了有关执行的拟合次数的有用输出,这使得计算工作量更加清晰。您共享的输出确认了网格搜索有效地探索了 5 折的各种 alpha 值,总共进行了 100 次模型拟合。
|
1 2 3 |
对 20 个候选值中的每个值进行 5 折拟合,总计 100 次拟合 Lasso 的最佳 alpha:17 最佳交叉验证得分:0.8881 |
alpha 值为 17 相对较高,这表明模型受益于更强的正则化水平。这可能表明数据集中存在一定程度的多重共线性或其他因素,使得模型简化(变量减少或系数变小)有利于提高预测准确性。
对于Ridge 模型,我们也调整了 alpha 参数,但在此它会影响L2 惩罚。与 L1 不同,L2 惩罚不会将系数归零;相反,它会减小系数的幅度,这有助于处理多重共线性和模型过拟合。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
#构建于上述代码块之上 # 对 Ridge 实现 GridSearchCV 以获得最佳 alpha from sklearn.model_selection import GridSearchCV # 定义 Ridge 的 alpha 范围 alpha = list(range(1, 21, 1)) # 范围从 1 到 20,增量为 1 # 设置 Ridge 的网格搜索 ridge_grid = GridSearchCV(estimator=pipelines['Ridge'], param_grid={'regressor__alpha': alpha}, verbose=1) # 打印进度 ridge_grid.fit(X, y) # 提取 Ridge 的最佳 alpha 和最佳得分 ridge_best_alpha = ridge_grid.best_params_['regressor__alpha'] ridge_best_score = ridge_grid.best_score_ print(f"Ridge 的最佳 alpha: {ridge_best_alpha}") print(f"最佳交叉验证得分: {round(ridge_best_score, 4)}") |
Ridge 回归的 GridSearchCV 结果显示最佳 alpha 为 3,交叉验证得分为 0.889。此得分略高于 Lasso 模型(alpha 为 17 时得分为 0.8881)。
|
1 2 3 |
对 20 个候选值中的每个值进行 5 折拟合,总计 100 次拟合 Ridge 的最佳 alpha:3 最佳交叉验证得分:0.889 |
Ridge 的最佳 alpha 值远低于 Lasso(3 对比 17),这表明该数据集可能受益于 Ridge 提供的较低强度的正则化方法。Ridge 正则化(L2)不会将系数缩减为零,而是缩小它们的幅度,这在许多特征具有预测能力(尽管幅度较小)时可能很有益。Ridge 在此案例中略优于 Lasso(0.889 对比 0.8881)的事实可能表明,特征消除(Lasso 通过将系数归零来实现)对于此数据集不如特征收缩(Ridge 实现)有益。这可能意味着大多数(如果不是全部)预测变量对目标变量都有一定程度的贡献。
ElasticNet 结合了 Lasso 和 Ridge 的惩罚,由 alpha 和 l1_ratio 控制。调整这些参数可以让我们在特征消除和特征收缩之间找到一个最佳点,从而利用 L1 和 L2 正则化的优点。
l1_ratio 参数是 ElasticNet 特有的。ElasticNet 是一个混合模型,它结合了 Lasso 和 Ridge 的惩罚。在此模型中
alpha仍然控制着惩罚的整体强度。l1_ratio指定了 L1 和 L2 正则化之间的平衡,其中l1_ratio = 1对应 Lasso,l1_ratio = 0对应 Ridge,- 介于两者之间的值可以调整两者的组合。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
#构建于上述代码块之上 # 对 ElasticNet 实现 GridSearchCV 以获得最佳参数 from sklearn.model_selection import GridSearchCV # 定义 ElasticNet 的 alpha 范围 alpha = list(range(1, 21, 1)) # 范围从 1 到 20,增量为 1 # 定义 ElasticNet 的 L1 比例范围 l1_ratio = [0.05, 0.5, 0.95] # 设置 ElasticNet 的网格搜索 elasticnet_grid = GridSearchCV(estimator=pipelines['ElasticNet'], param_grid={'regressor__alpha': alpha, 'regressor__l1_ratio': l1_ratio}, verbose=1) # 打印进度 elasticnet_grid.fit(X, y) # 提取 ElasticNet 的最佳参数和最佳得分 elasticnet_best_params = elasticnet_grid.best_params_ elasticnet_best_score = elasticnet_grid.best_score_ print(f"ElasticNet 的最佳参数: {elasticnet_best_params}") print(f"最佳交叉验证得分: {round(elasticnet_best_score, 4)}") |
在调整之前,ElasticNet 的初始设置的交叉验证 R² 得分为 0.8299。这明显低于 Lasso 和 Ridge 的得分,表明默认参数可能不是该模型在埃姆斯住房数据集上的最佳参数。调整后,ElasticNet 的最佳参数将其得分提高到了 0.8762。
|
1 2 3 |
对 60 个候选值中的每个值进行 5 折拟合,总计 300 次拟合 ElasticNet 的最佳参数:{'regressor__alpha': 1, 'regressor__l1_ratio': 0.95} 最佳交叉验证得分:0.8762 |
从 0.8299 到 0.8762 的提升表明微调超参数对模型性能有显著影响。这凸显了超参数优化的必要性,特别是在 ElasticNet 这样平衡两种正则化类型的模型中。调整有效地调整了 L1 和 L2 惩罚之间的平衡,找到了一个更适合数据集的配置。虽然调整后的模型性能未能超过最佳的 Ridge 模型(得分为 0.889),但它大大缩小了差距,表明通过正确的参数,ElasticNet 可以与更简单的正则化模型进行密切竞争。
进一步阅读
API
- sklearn.preprocessing.StandardScaler API
- sklearn.linear_model.Lasso API
- sklearn.linear_model.Ridge API
- sklearn.linear_model.ElasticNet API
- sklearn.model_selection.GridSearchCV API
教程
资源
总结
在本指南中,我们使用埃姆斯住房数据集,探讨了惩罚性回归模型—Lasso、Ridge 和 ElasticNet—的应用和优化。我们首先强调了特征缩放的重要性,以确保所有特征的贡献相等。通过设置 scikit-learn 流水线,我们展示了不同模型在基本配置下的表现,其中 Ridge 最初略优于其他模型。然后,我们专注于超参数调整,这不仅通过调整 alpha 和 l1_ratio 显著提高了 ElasticNet 的性能,还加深了我们对不同模型在各种配置下行为的理解。这些见解至关重要,因为它们有助于为特定的数据集和预测目标选择合适的模型和设置,这表明超参数调整不仅仅是为了获得更高的准确性,更是为了理解模型动态。
具体来说,你学到了:
- 特征缩放对于惩罚性模型的情境下的关键作用。
- 如何使用
scikit-learn流水线实现 Lasso、Ridge 和 ElasticNet 模型。 - 如何使用
GridSearchCV和超参数调整优化模型性能。
您有任何问题吗?请在下面的评论中提出您的问题,我将尽力回答。






暂无评论。