Python 是一种通用计算语言，但在科学计算领域非常受欢迎。得益于 Python 生态系统中的一些库，在许多情况下它可以取代 R 和 Matlab。在机器学习中，我们广泛使用一些数学或统计函数，并且通常会发现 NumPy 和 SciPy 非常有用。下面，我们将简要概述 NumPy 和 SciPy 提供的内容以及一些使用技巧。
完成本教程后，您将了解
- NumPy 和 SciPy 为您的项目提供什么
- 如何使用 numba 快速加速 NumPy 代码
通过我的新书 Python for Machine Learning 快速启动您的项目，其中包括分步教程和所有示例的Python 源代码文件。
让我们开始吧！
NumPy 和 SciPy 中的科学函数
照片由 Nothing Ahead 提供。保留部分权利。
概述
本教程分为三个部分
- NumPy 作为张量库
- SciPy 中的函数
- 使用 numba 加速
NumPy 作为张量库
虽然 Python 中的列表和元组是我们原生管理数组的方式，但 NumPy 提供了更接近 C 或 Java 的数组功能，因为我们可以强制要求所有元素具有相同的数据类型，并且在处理高维数组时，在每个维度上都具有规则的形状。此外，在 NumPy 数组上执行相同操作通常比在 Python 中原生执行更快，因为 NumPy 中的代码经过高度优化。
NumPy 提供了成千上万个函数，您应该查阅 NumPy 的文档以获取详细信息。以下备忘单中包含一些常见用法
NumPy 备忘单。版权所有 2022 MachineLearningMastery.com
NumPy 有一些很酷的功能值得一提，因为它们对机器学习项目很有帮助。
例如，如果我们想绘制一个 3D 曲线，我们会计算 $z=f(x,y)$ 对于一系列 $x$ 和 $y$，然后将其结果绘制在 $xyz$ 空间中。我们可以这样生成范围
|
1 2 3 |
import numpy as np x = np.linspace(-1, 1, 100) y = np.linspace(-2, 2, 100) |
对于 $z=f(x,y)=\sqrt{1-x^2-(y/2)^2}$，我们可能需要一个嵌套的 for 循环来扫描数组 `x` 和 `y` 中的每个值并进行计算。但在 NumPy 中，我们可以使用 `meshgrid` 将两个一维数组扩展成两个二维数组，通过匹配索引，我们可以获得所有组合，如下所示
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
导入 matplotlib.pyplot 为 plt import numpy as np x = np.linspace(-1, 1, 100) y = np.linspace(-2, 2, 100) # 将向量转换为二维数组 xx, yy = np.meshgrid(x,y) # 匹配项上的计算 z = np.sqrt(1 - xx**2 - (yy/2)**2) fig = plt.figure(figsize=(8,8)) ax = plt.axes(projection='3d') ax.set_xlim([-2,2]) ax.set_ylim([-2,2]) ax.set_zlim([0,2]) ax.plot_surface(xx, yy, z, cmap="cividis") ax.view_init(45, 35) plt.show() |
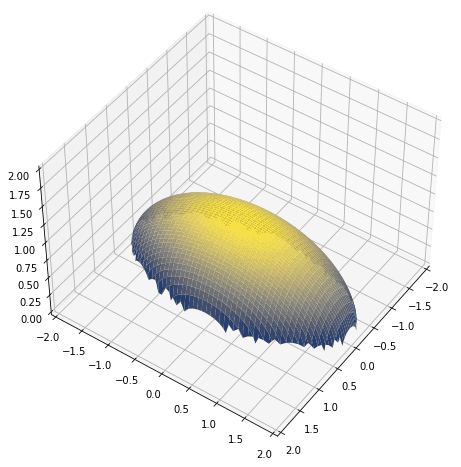
在上面，`meshgrid()` 生成的二维数组 `xx` 在同一列上具有相同的值，而 `yy` 在同一行上具有相同的值。因此，对 `xx` 和 `yy` 的逐元素操作本质上是对 $xy$-平面进行的操作。这就是它有效的原因，以及我们为什么可以绘制上面的椭球体。
NumPy 中的另一个好功能是用于扩展维度的函数。神经网络中的卷积层通常期望 3D 图像，即 2D 像素，以及作为第三维的不同颜色通道。它适用于具有 RGB 通道彩色图像，但对于灰度图像我们只有一个通道。例如，scikit-learn 中的 digits 数据集
|
1 2 3 |
from sklearn.datasets import load_digits images = load_digits()["images"] print(images.shape) |
|
1 |
(1797, 8, 8) |
这表明该数据集有 1797 张图像，每张图像为 8x8 像素。这是一个灰度数据集，显示每个像素是暗度值。我们将第 4 轴添加到此数组（即，将 3D 数组转换为 4D 数组），以便每张图像为 8x8x1 像素
|
1 2 3 4 5 |
... # 图像有轴 0、1 和 2，添加轴 3 images = np.expand_dims(images, 3) print(images.shape) |
|
1 |
(1797, 8, 8, 1) |
使用 NumPy 数组时的一个便捷功能是布尔索引和花式索引。例如，如果我们有一个二维数组
|
1 2 3 4 5 6 7 8 |
import numpy as np X = np.array([ [ 1.299, 0.332, 0.594, -0.047, 0.834], [ 0.842, 0.441, -0.705, -1.086, -0.252], [ 0.785, 0.478, -0.665, -0.532, -0.673], [ 0.062, 1.228, -0.333, 0.867, 0.371] ]) |
我们可以检查一列中的所有值是否为正
|
1 2 3 |
... y = (X > 0).all(axis=0) print(y) |
|
1 |
array([ True, True, False, False, False]) |
这表明只有前两列是全正的。请注意，这是一个长度为 5 的一维数组，与数组 `X` 的轴 1 大小相同。如果我们使用此布尔数组作为轴 1 的索引，我们将仅选择索引为正的子数组
|
1 2 3 |
... y = X[:, (X > 0).all(axis=0) print(y) |
|
1 2 3 4 |
array([[1.299, 0.332], [0.842, 0.441], [0.785, 0.478], [0.062, 1.228]]) |
如果使用整数列表代替上述布尔数组，我们将根据匹配列表的索引从 `X` 中选择。NumPy 将此称为花式索引。因此，下面我们可以选择前两列两次，形成一个新数组
|
1 2 3 |
... y = X[:, [0,1,1,0]] print(y) |
|
1 2 3 4 |
array([[1.299, 0.332, 0.332, 1.299], [0.842, 0.441, 0.441, 0.842], [0.785, 0.478, 0.478, 0.785], [0.062, 1.228, 1.228, 0.062]]) |
SciPy 中的函数
SciPy 是 NumPy 的姊妹项目。因此，您将主要看到 SciPy 函数接受 NumPy 数组作为参数或返回 NumPy 数组。SciPy 提供了许多不常用或更高级的函数。
SciPy 函数组织在子模块下。一些常见的子模块是
scipy.cluster.hierarchy：层次聚类scipy.fft：快速傅里叶变换scipy.integrate：数值积分scipy.interpolate：插值和样条函数scipy.linalg：线性代数scipy.optimize：数值优化scipy.signal：信号处理scipy.sparse：稀疏矩阵表示scipy.special：一些奇异数学函数scipy.stats：统计，包括概率分布
但永远不要假设 SciPy 能覆盖一切。例如，对于时间序列分析，最好依赖 `statsmodels` 模块。
我们在其他帖子中介绍了许多使用 `scipy.optimize` 的示例。它是一个很好的工具，可以通过例如牛顿法来查找函数的最小值。NumPy 和 SciPy 都有用于线性代数的 `linalg` 子模块，但 SciPy 中的函数更高级，例如用于 QR 分解或矩阵指数的函数。
也许 SciPy 最常用的功能是 `stats` 模块。在 NumPy 和 SciPy 中，我们都可以生成具有非零相关性的多元高斯随机数。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
import numpy as np from scipy.stats import multivariate_normal import matplotlib.pyplot as plt mean = [0, 0] # 零均值 cov = [[1, 0.8],[0.8, 1]] # 协方差矩阵 X1 = np.random.default_rng().multivariate_normal(mean, cov, 5000) X2 = multivariate_normal.rvs(mean, cov, 5000) fig = plt.figure(figsize=(12,6)) ax = plt.subplot(121) ax.scatter(X1[:,0], X1[:,1], s=1) ax.set_xlim([-4,4]) ax.set_ylim([-4,4]) ax.set_title("NumPy") ax = plt.subplot(122) ax.scatter(X2[:,0], X2[:,1], s=1) ax.set_xlim([-4,4]) ax.set_ylim([-4,4]) ax.set_title("SciPy") plt.show() |
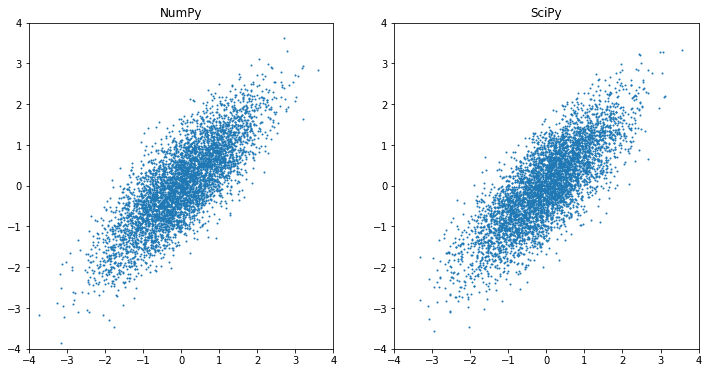
但是，如果我们想引用分布函数本身，最好依赖 SciPy。例如，著名的 68-95-99.7 法则是指标准正态分布，我们可以从 SciPy 的累积分布函数中获得确切的百分比
|
1 2 3 4 |
from scipy.stats import norm n = norm.cdf([1,2,3,-1,-2,-3]) print(n) print(n[:3] - n[-3:]) |
|
1 2 |
[0.84134475 0.97724987 0.9986501 0.15865525 0.02275013 0.0013499 ] [0.68268949 0.95449974 0.9973002 ] |
因此，我们看到在正态分布中，我们期望值落在均值一个标准差以内的概率为 68.269%。反之，我们有百分点函数作为累积分布函数的反函数
|
1 2 |
... print(norm.ppf(0.99)) |
|
1 |
2.3263478740408408 |
这意味着，如果数值服从正态分布，我们预计有 99% 的概率（单尾概率）数值不会超过均值 2.32 个标准差。
这些是 SciPy 如何在 NumPy 提供的功能之上更进一步的示例。
想开始学习机器学习 Python 吗？
立即参加我为期7天的免费电子邮件速成课程（附示例代码）。
点击注册，同时获得该课程的免费PDF电子书版本。
使用 numba 加速
NumPy 比原生 Python 更快，因为许多操作是用 C 实现的，并且使用了优化的算法。但有时我们想做一些事情，但 NumPy 仍然太慢。
如果你让 `numba` 通过并行化或将操作移动到 GPU（如果你有 GPU）来进一步优化它，可能会有帮助。你需要先安装 `numba` 模块
|
1 |
pip install numba |
如果你需要将 `numba` 编译成 Python 模块，可能需要一些时间。之后，如果你的函数仅包含 NumPy 操作，你可以添加 `numba` 装饰器来加速它
|
1 2 3 4 5 |
import numba @numba.jit(nopython=True) def numpy_only_function(...) ... |
它的作用是使用即时编译器来向量化操作，以便它可以运行得更快。如果你的函数在程序中运行很多次（例如，梯度下降中的更新函数），你可以看到最佳的性能提升，因为运行编译器的开销可以被摊销。
例如，下面是一个 t-SNE 算法的实现，用于将 784 维数据转换为 2 维。我们不打算详细解释 t-SNE 算法，但它需要许多迭代才能收敛。下面的代码展示了如何使用 `numba` 来优化内部循环函数（并且它也展示了一些 NumPy 的用法）。完成需要几分钟。之后你可以尝试删除 `@numba.jit` 装饰器。这将花费更长的时间。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 |
import datetime import tensorflow as tf import matplotlib.pyplot as plt import numpy as np import numba def tSNE(X, ndims=2, perplexity=30, seed=0, max_iter=500, stop_lying_iter=100, mom_switch_iter=400): """t-SNE 算法 参数 X: 高维坐标 ndims: 输出域的维度数 返回 低维度的 X 中的点 """ momentum = 0.5 final_momentum = 0.8 eta = 200.0 N, _D = X.shape np.random.seed(seed) # 归一化输入 X -= X.mean(axis=0) # 零均值 X /= np.abs(X).max() # 最小-最大缩放 # 计算精确 t-SNE 的输入相似性 P = computeGaussianPerplexity(X, perplexity) # 对称化并归一化输入相似性 P = P + P.T P /= P.sum() # 虚构 P 值 P *= 12.0 # 初始化解 Y = np.random.randn(N, ndims) * 0.0001 # 执行主训练循环 gains = np.ones_like(Y) uY = np.zeros_like(Y) for i in range(max_iter): # 计算梯度，更新增益 dY = computeExactGradient(P, Y) gains = np.where(np.sign(dY) != np.sign(uY), gains+0.2, gains*0.8).clip(0.1) # 梯度更新，包括动量和增益 uY = momentum * uY - eta * gains * dY Y = Y + uY # 使解零均值 Y -= Y.mean(axis=0) # 在一段时间后停止虚构 P 值，并切换动量 if i == stop_lying_iter: P /= 12.0 if i == mom_switch_iter: momentum = final_momentum # 打印进度 if (i % 50) == 0: C = evaluateError(P, Y) now = datetime.datetime.now() print(f"{now} - Iteration {i}: Error = {C}") return Y @numba.jit(nopython=True) def computeExactGradient(P, Y): """t-SNE 损失函数的梯度 参数 P: 相似度矩阵 Y: 低维坐标 返回 dY, 一个形状为 (N,D) 的 numpy 数组 """ N, _D = Y.shape # 计算 Y 的平方欧氏距离矩阵、Q 矩阵以及归一化总和 DD = computeSquaredEuclideanDistance(Y) Q = 1/(1+DD) sum_Q = Q.sum() # 计算梯度 mult = (P - (Q/sum_Q)) * Q dY = np.zeros_like(Y) for n in range(N): for m in range(N): if n==m: continue dY[n] += (Y[n] - Y[m]) * mult[n,m] return dY @numba.jit(nopython=True) def evaluateError(P, Y): """评估 t-SNE 成本函数 参数 P: 相似度矩阵 Y: 低维坐标 返回 总 t-SNE 误差 C """ DD = computeSquaredEuclideanDistance(Y) # 计算 Q 矩阵和归一化总和 Q = 1/(1+DD) np.fill_diagonal(Q, np.finfo(np.float32).eps) Q /= Q.sum() # 计算 t-SNE 误差：sum P log(P/Q) error = P * np.log( (P + np.finfo(np.float32).eps) / (Q + np.finfo(np.float32).eps) ) return error.sum() @numba.jit(nopython=True) def computeGaussianPerplexity(X, perplexity): """计算高斯困惑度 参数 X: 形状为 (N,D) 的 numpy 数组 perplexity: 双精度浮点数 返回 相似度矩阵 P """ # 计算平方欧氏距离矩阵 N, _D = X.shape DD = computeSquaredEuclideanDistance(X) # 逐行计算高斯核 P = np.zeros_like(DD) for n in range(N): found = False beta = 1.0 min_beta = -np.inf max_beta = np.inf tol = 1e-5 # 迭代直到获得合适的困惑度 n_iter = 0 while not found and n_iter < 200: # 计算高斯核行 P[n] = np.exp(-beta * DD[n]) P[n,n] = np.finfo(np.float32).eps # 计算当前行的熵 # 高斯需要行归一化，使其成为概率 # 然后 H = sum_i -P[i] log(P[i]) # = sum_i -P[i] (-beta * DD[n] - log(sum_P)) # = sum_i P[i] * beta * DD[n] + log(sum_P) sum_P = P[n].sum() H = beta * (DD[n] @ P[n]) / sum_P + np.log(sum_P) # 评估熵是否在容差范围内 Hdiff = H - np.log2(perplexity) if -tol < Hdiff < tol: found = True break if Hdiff > 0: min_beta = beta if max_beta in (np.inf, -np.inf): beta *= 2 else: beta = (beta + max_beta) / 2 else: max_beta = beta if min_beta in (np.inf, -np.inf): beta /= 2 else: beta = (beta + min_beta) / 2 n_iter += 1 # 归一化此行 P[n] /= P[n].sum() assert not np.isnan(P).any() return P @numba.jit(nopython=True) def computeSquaredEuclideanDistance(X): """计算平方距离 参数 X: 形状为 (N,D) 的 numpy 数组 返回 形状为 (N,N) 的平方距离的 numpy 数组 """ N, _D = X.shape DD = np.zeros((N,N)) for i in range(N-1): for j in range(i+1, N): diff = X[i] - X[j] DD[j][i] = DD[i][j] = diff @ diff return DD (X_train, y_train), (X_test, y_test) = tf.keras.datasets.mnist.load_data() # 从数据集中选择 1000 个样本 rows = np.random.choice(X_test.shape[0], 1000, replace=False) X_data = X_train[rows].reshape(1000, -1).astype("float") X_label = y_train[rows] # 运行 t-SNE 将其转换为 2D 并可视化在散点图中 Y = tSNE(X_data, 2, 30, 0, 500, 100, 400) plt.figure(figsize=(8,8)) plt.scatter(Y[:,0], Y[:,1], c=X_label) plt.show() |
进一步阅读
如果您想深入了解，本节提供了更多关于该主题的资源。
API 文档
总结
在本教程中，您简要了解了 NumPy 和 SciPy 提供的函数。
具体来说，你学到了：
- 如何使用 NumPy 数组
- SciPy 提供的一些实用函数
- 如何通过使用 numba 的 JIT 编译器来加速 NumPy 代码
掌握机器学习 Python！
更自信地用 Python 编写代码
...从学习实用的 Python 技巧开始
在我的新电子书中探索如何实现
用于机器学习的 Python
它提供自学教程和数百个可运行的代码，为您提供包括以下技能：
调试、性能分析、鸭子类型、装饰器、部署等等...
好文章！请更新 NumPy 关于随机数生成器的部分。Randint、randn 等在新代码中不应使用。np.random.Generator 应在新代码中使用 :)
感谢 Pamphile 的反馈！