使用 Python 进行季节性持续性预测

作者 Jason Brownlee 于 2019年8月28日发表于时间序列 22

使用持续性或朴素预测作为时间序列问题的初步预测是很常见的。

对于具有季节性成分的时间序列数据，一个更好的初步预测是持续上一季度的相同时间点的观测值。这被称为季节性持续性。

在本教程中，您将了解如何在 Python 中为时间序列预测实现季节性持续性。

完成本教程后，您将了解：

如何使用先前季节的定点观测值进行持续性预测。
如何使用先前季节的滑动窗口中的平均观测值进行持续性预测。
如何对月度和日度时间序列数据应用和评估季节性持续性。

通过我的新书《Python 时间序列预测入门》，开始您的项目，其中包含分步教程和所有示例的Python源代码文件。

让我们开始吧。

2019 年 4 月更新：更新了数据集链接。
2019年8月更新：更新了数据加载以使用新的API。

季节性持续性

在时间序列问题上拥有有用的初步预测至关重要，可以为技能设定一个较低的基准，然后才能转向更复杂的方法。

这是为了确保我们不会在无预测能力的模型或数据集上浪费时间。

在进行时间序列预测时，通常使用持续性或朴素预测作为初步预测模型。

对于具有明显季节性成分的时间序列数据，这没有意义。对于季节性数据，更好的初步模型是使用上一季节周期相同时间点的观测值作为预测。

我们可以称之为“季节性持续性”，它是一个简单的模型，可以作为有效的初步模型。

一步改进是使用先前季节相同时间点的最后几次观测值的简单函数。例如，观测值的平均值。这通常可以提供一些额外的收益。

在本教程中，我们将演示这种简单的季节性持续性预测方法，为三个不同的真实世界时间序列数据集提供预测技能的较低基准。

滑动窗口季节性持续性

在本教程中，我们将使用滑动窗口季节性持续性模型进行预测。

在滑动窗口内，将收集先前一年相同时间点的观测值，并将这些观测值的平均值用作持续预测。

可以评估不同的窗口大小，以找到最小化误差的组合。

例如，如果数据是月度数据，并且要预测的月份是二月，那么对于窗口大小为 1 (w=1) 的情况，将使用去年二月的观测值进行预测。

窗口大小为 2 (w=2) 将涉及取过去两个二月的观测值进行平均，并用作预测。

另一种解释可能是尝试使用先前年份的定点观测值（例如，月度数据的 t-12、t-24 等），而不是对累积定点观测值取平均值。也许可以在您的数据集上尝试这两种方法，看看哪种作为良好的起点模型效果更好。

停止以慢速学习时间序列预测！

参加我的免费7天电子邮件课程，了解如何入门（附带示例代码）。

点击注册，同时获得该课程的免费PDF电子书版本。

实验测试框架

一致地评估时间序列预测模型很重要。

在本节中，我们将定义在本教程中如何评估预测模型。

首先，我们将预留最后两年的数据，并在这些数据上评估预测。这对于我们将要查看的月度和日度数据都适用。

我们将使用前向验证来评估模型性能。这意味着测试数据集中的每个时间步都将被枚举，在历史数据上构建模型，并将预测与预期值进行比较。然后，该观测值将被添加到训练数据集中，并重复该过程。

前向验证是评估时间序列预测模型的一种现实方法，因为当新观测值可用时，模型会进行更新。

最后，将使用均方根误差 (RMSE) 来评估预测。RMSE 的好处是它会惩罚较大的误差，并且分数与预测值（每月汽车销量）的单位相同。

总之，测试框架包括：

最后 2 年的数据用作测试集。
前向验证用于模型评估。
使用均方根误差来报告模型技能。

案例研究 1：月度汽车销售数据集

月度汽车销售数据集描述了 1960 年至 1968 年间加拿大魁北克省的汽车销量。

单位是销售数量，共有 108 个观测值。数据来源归功于 Abraham 和 Ledolter (1983)。

下载数据集

下载数据集并将其保存到当前工作目录，文件名为“car-sales.csv”。请注意，您可能需要从文件中删除页脚信息。

下面的代码将数据集加载为 Pandas Series 对象。

# line plot of time series
from pandas import read_csv
from matplotlib import pyplot
# load dataset
series = read_csv('car-sales.csv', header=0, index_col=0)
# display first few rows
print(series.head(5))
# line plot of dataset
series.plot()
pyplot.show()

# 时间序列的折线图

from pandas import read_csv

from matplotlib import pyplot

# 加载数据集

series = read_csv('car-sales.csv', header=0, index_col=0)

# 显示前几行

print(series.head(5))

# 数据集的折线图

series.plot()

pyplot.show()

运行示例将打印数据的前5行。

Month
1960-01-01 6550
1960-02-01 8728
1960-03-01 12026
1960-04-01 14395
1960-05-01 14587
Name: Sales, dtype: int64

月份

1960-01-01 6550

1960-02-01 8728

1960-03-01 12026

1960-04-01 14395

1960-05-01 14587

Name: Sales, dtype: int64

还提供了数据的折线图。我们可以看到年度季节性成分和增长趋势。

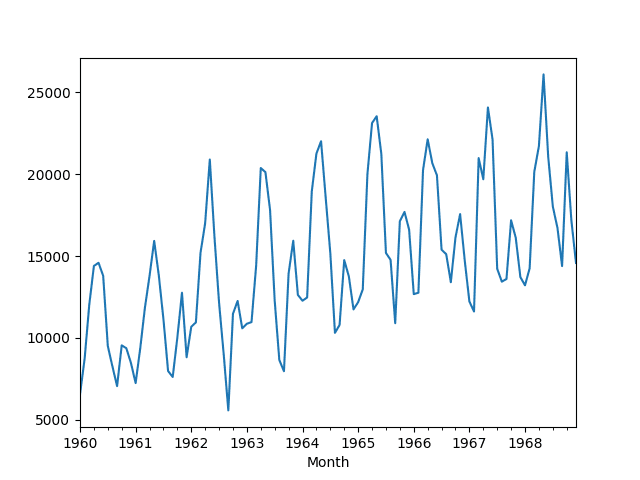
月度汽车销售数据集折线图

将预留最后 24 个月的月度数据作为测试数据。我们将研究 1 到 5 年的滑动窗口季节性持续性。

完整的示例如下所示。

from pandas import read_csv
from sklearn.metrics import mean_squared_error
from math import sqrt
from numpy import mean
from matplotlib import pyplot
# load data
series = read_csv('car-sales.csv', header=0, index_col=0)
# prepare data
X = series.values
train, test = X[0:-24], X[-24:]
# evaluate mean of different number of years
years = [1, 2, 3, 4, 5]
scores = list()
for year in years:
	# walk-forward validation
	history = [x for x in train]
	predictions = list()
	for i in range(len(test)):
		# collect obs
		obs = list()
		for y in range(1, year+1):
			obs.append(history[-(y*12)])
		# make prediction
		yhat = mean(obs)
		predictions.append(yhat)
		# observation
		history.append(test[i])
	# report performance
	rmse = sqrt(mean_squared_error(test, predictions))
	scores.append(rmse)
	print('Years=%d, RMSE: %.3f' % (year, rmse))
pyplot.plot(years, scores)
pyplot.show()

from pandas import read_csv

from sklearn.metrics import mean_squared_error

from math import sqrt

from numpy import mean

from matplotlib import pyplot

# 加载数据

series = read_csv('car-sales.csv', header=0, index_col=0)

# 准备数据

X = series.values

train, test = X[0:-24], X[-24:]

# 评估不同年数的平均值

years = [1, 2, 3, 4, 5]

scores = list()

for year in years:

# 前向验证

history = [x for x in train]

predictions = list()

for i in range(len(test)):

# 收集观测值

obs = list()

for y in range(1, year+1):

obs.append(history[-(y*12)])

# 进行预测

yhat = mean(obs)

predictions.append(yhat)

# 观测

history.append(test[i])

# 报告性能

rmse = sqrt(mean_squared_error(test, predictions))

scores.append(rmse)

print('Years=%d, RMSE: %.3f' % (year, rmse))

pyplot.plot(years, scores)

pyplot.show()

运行示例会打印年份和过去几年相同月份的观测值滑动窗口的平均值季节性持续性模型误差。

结果表明，从最后三年平均值开始是一个不错的模型，RMSE 为 1803.630 辆汽车销量。

Years=1, RMSE: 1997.732
Years=2, RMSE: 1914.911
Years=3, RMSE: 1803.630
Years=4, RMSE: 2099.481
Years=5, RMSE: 2522.235

Years=1, RMSE: 1997.732

Years=2, RMSE: 1914.911

Years=3, RMSE: 1803.630

Years=4, RMSE: 2099.481

Years=5, RMSE: 2522.235

创建了一个滑动窗口大小与模型误差之间关系的图。

该图很好地显示了随着滑动窗口大小增加到 3 年而带来的改进，然后从该点开始误差急剧增加。

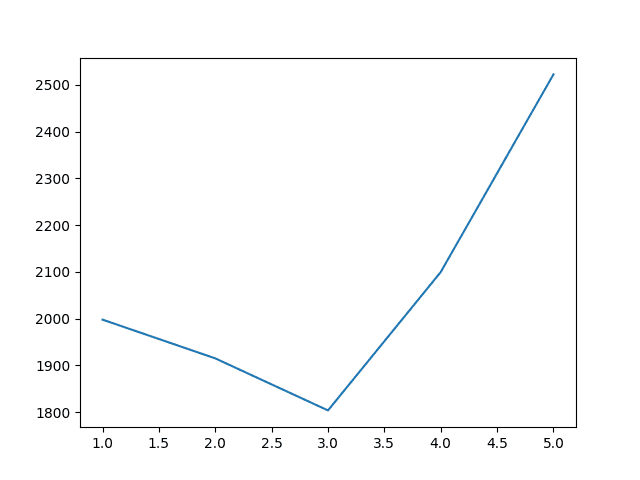
Sliding Window Size to RMSE for Monthly Car Sales

月度汽车销售的滑动窗口大小与 RMSE

案例研究 2：月度书写纸销售数据集

月度书写纸销售数据集描述了特种书写纸的销量。

单位是销售数量，共有 147 个月（略多于 12 年）的观测值。计数是小数，表明数据实际上可能以十万销量为单位。数据来源归功于 Makridakis 和 Wheelwright (1989)。

下载数据集.

下载数据集并将其保存到当前工作目录，文件名为“writing-paper-sales.csv”。请注意，您可能需要从文件中删除页脚信息。

日期时间戳仅包含年份和月份。因此，需要一个自定义日期时间解析函数来加载数据并基于任意年份的数据。选择 1900 年作为起点，这不应影响本案例研究。

下面的示例加载月度书写纸销售数据集作为 Pandas Series。

# load and plot dataset
from pandas import read_csv
from pandas import datetime
from matplotlib import pyplot
# load dataset
def parser(x):
	if len(x) == 4:
		return datetime.strptime('190'+x, '%Y-%m')
	return datetime.strptime('19'+x, '%Y-%m')
series = read_csv('writing-paper-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)
# summarize first few rows
print(series.head())
# line plot
series.plot()
pyplot.show()

# 加载并绘制数据集

from pandas import read_csv

from pandas import datetime

from matplotlib import pyplot

# 加载数据集

def parser(x):

if len(x) == 4:

return datetime.strptime('190'+x, '%Y-%m')

return datetime.strptime('19'+x, '%Y-%m')

series = read_csv('writing-paper-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)

# 总结前几行

print(series.head())

# 线图

series.plot()

pyplot.show()

运行示例会打印加载数据集的前 5 行。

Month
1901-01-01 1359.795
1901-02-01 1278.564
1901-03-01 1508.327
1901-04-01 1419.710
1901-05-01 1440.510

月份

1901-01-01 1359.795

1901-02-01 1278.564

1901-03-01 1508.327

1901-04-01 1419.710

1901-05-01 1440.510

然后创建加载数据集的折线图。我们可以看到年度季节性成分和增长趋势。

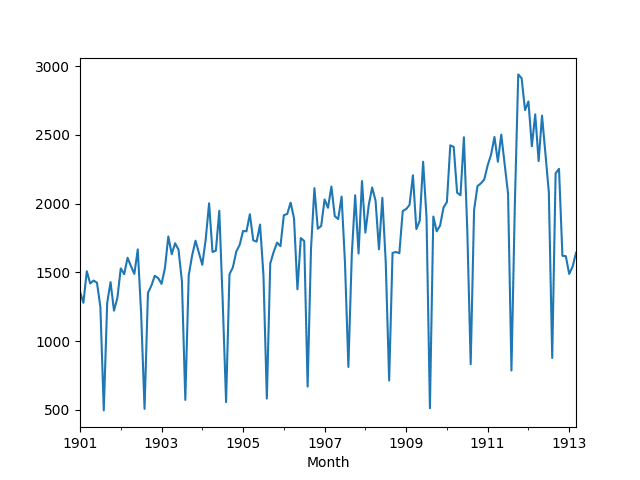
Line Plot of Monthly Writing Paper Sales Dataset

月度书写纸销售数据集折线图

与前面的示例一样，我们可以将最后 24 个月的观测值作为测试数据集。因为我们有更多的数据，所以我们将尝试 1 年到 10 年的滑动窗口大小。

完整的示例如下所示。

from pandas import read_csv
from pandas import datetime
from sklearn.metrics import mean_squared_error
from math import sqrt
from numpy import mean
from matplotlib import pyplot
# load dataset
def parser(x):
	if len(x) == 4:
		return datetime.strptime('190'+x, '%Y-%m')
	return datetime.strptime('19'+x, '%Y-%m')
series = read_csv('writing-paper-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)
# prepare data
X = series.values
train, test = X[0:-24], X[-24:]
# evaluate mean of different number of years
years = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
scores = list()
for year in years:
	# walk-forward validation
	history = [x for x in train]
	predictions = list()
	for i in range(len(test)):
		# collect obs
		obs = list()
		for y in range(1, year+1):
			obs.append(history[-(y*12)])
		# make prediction
		yhat = mean(obs)
		predictions.append(yhat)
		# observation
		history.append(test[i])
	# report performance
	rmse = sqrt(mean_squared_error(test, predictions))
	scores.append(rmse)
	print('Years=%d, RMSE: %.3f' % (year, rmse))
pyplot.plot(years, scores)
pyplot.show()

from pandas import read_csv

from pandas import datetime

from sklearn.metrics import mean_squared_error

from math import sqrt

from numpy import mean

from matplotlib import pyplot

# 加载数据集

def parser(x):

if len(x) == 4:

return datetime.strptime('190'+x, '%Y-%m')

return datetime.strptime('19'+x, '%Y-%m')

series = read_csv('writing-paper-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)

# 准备数据

X = series.values

train, test = X[0:-24], X[-24:]

# 评估不同年数的平均值

years = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

scores = list()

for year in years:

# 前向验证

history = [x for x in train]

predictions = list()

for i in range(len(test)):

# 收集观测值

obs = list()

for y in range(1, year+1):

obs.append(history[-(y*12)])

# 进行预测

yhat = mean(obs)

predictions.append(yhat)

# 观测

history.append(test[i])

# 报告性能

rmse = sqrt(mean_squared_error(test, predictions))

scores.append(rmse)

print('Years=%d, RMSE: %.3f' % (year, rmse))

pyplot.plot(years, scores)

pyplot.show()

运行示例会打印滑动窗口的大小以及由此产生的季节性持续性模型误差。

结果表明，5 年的窗口大小是最佳的，RMSE 为 554.660 月度书写纸销量。

Years=1, RMSE: 606.089
Years=2, RMSE: 557.653
Years=3, RMSE: 555.777
Years=4, RMSE: 544.251
Years=5, RMSE: 540.317
Years=6, RMSE: 554.660
Years=7, RMSE: 569.032
Years=8, RMSE: 581.405
Years=9, RMSE: 602.279
Years=10, RMSE: 624.756

Years=1, RMSE: 606.089

Years=2, RMSE: 557.653

Years=3, RMSE: 555.777

Years=4, RMSE: 544.251

Years=5, RMSE: 540.317

Years=6, RMSE: 554.660

Years=7, RMSE: 569.032

Years=8, RMSE: 581.405

Years=9, RMSE: 602.279

Years=10, RMSE: 624.756

误差与窗口大小的关系被绘制在折线图上，显示出与前一个场景类似的误差趋势。误差下降到一个拐点（在本例中为 5 年），然后再次增加。

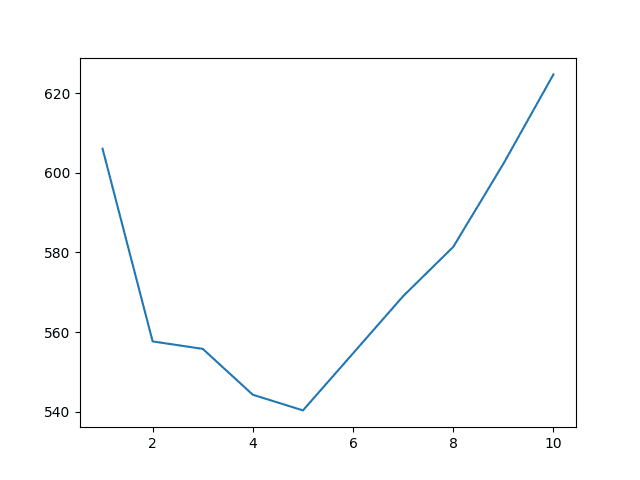
Sliding Window Size to RMSE for Monthly Writing Paper Sales

月度书写纸销售的滑动窗口大小与 RMSE

案例研究 3：每日墨尔本最高温度数据集

每日墨尔本最高温度数据集描述了 1981 年至 1990 年澳大利亚墨尔本市的每日温度。

单位是摄氏度，共有 3,650 个观测值，即 10 年的数据。数据来源归功于澳大利亚气象局。

下载数据集.

下载数据集并将其保存到当前工作目录，文件名为“max-daily-temps.csv”。请注意，您可能需要从文件中删除页脚信息。

下面的示例演示了如何将数据集加载为 Pandas Series。

# line plot of time series
from pandas import read_csv
from matplotlib import pyplot
# load dataset
series = read_csv('max-daily-temps.csv', header=0, index_col=0)
# display first few rows
print(series.head(5))
# line plot of dataset
series.plot()
pyplot.show()

# 时间序列的折线图

from pandas import read_csv

from matplotlib import pyplot

# 加载数据集

series = read_csv('max-daily-temps.csv', header=0, index_col=0)

# 显示前几行

print(series.head(5))

# 数据集的折线图

series.plot()

pyplot.show()

运行示例将打印数据的前5行。

Date
1981-01-01 38.1
1981-01-02 32.4
1981-01-03 34.5
1981-01-04 20.7
1981-01-05 21.5

日期

1981-01-01 38.1

1981-01-02 32.4

1981-01-03 34.5

1981-01-04 20.7

1981-01-05 21.5

还创建了一个折线图。我们可以看到比前两个场景有更多的观测值，并且数据中存在明显的季节性趋势。

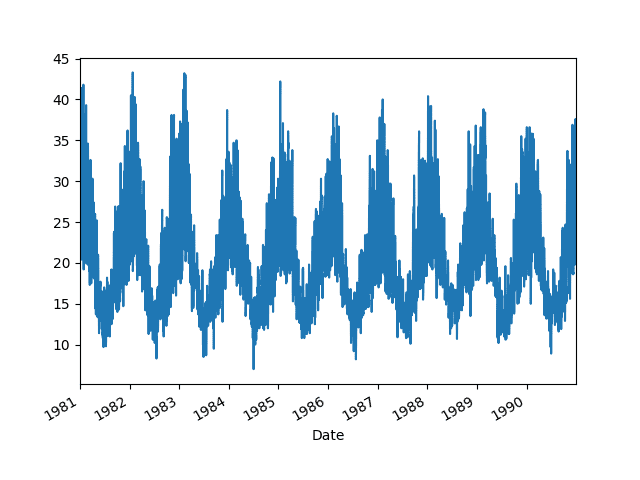
Line Plot of Daily Melbourne Maximum Temperatures Dataset

每日墨尔本最高温度数据集折线图

由于数据是每日的，我们需要将测试数据中的年份指定为 365 天的函数，而不是 12 个月。

这忽略了闰年，这是一个复杂的问题，在您自己的项目中可能会或应该得到解决。

下面列出了完整的季节性持续性示例。

from pandas import read_csv
from sklearn.metrics import mean_squared_error
from math import sqrt
from numpy import mean
from matplotlib import pyplot
# load data
series = read_csv('max-daily-temps.csv', header=0, index_col=0)
# prepare data
X = series.values
train, test = X[0:-(2*365)], X[-(2*365):]
# evaluate mean of different number of years
years = [1, 2, 3, 4, 5, 6, 7, 8]
scores = list()
for year in years:
	# walk-forward validation
	history = [x for x in train]
	predictions = list()
	for i in range(len(test)):
		# collect obs
		obs = list()
		for y in range(1, year+1):
			obs.append(history[-(y*365)])
		# make prediction
		yhat = mean(obs)
		predictions.append(yhat)
		# observation
		history.append(test[i])
	# report performance
	rmse = sqrt(mean_squared_error(test, predictions))
	scores.append(rmse)
	print('Years=%d, RMSE: %.3f' % (year, rmse))
pyplot.plot(years, scores)
pyplot.show()

from pandas import read_csv

from sklearn.metrics import mean_squared_error

from math import sqrt

from numpy import mean

from matplotlib import pyplot

# 加载数据

series = read_csv('max-daily-temps.csv', header=0, index_col=0)

# 准备数据

X = series.values

train, test = X[0:-(2*365)], X[-(2*365):]

# 评估不同年数的平均值

years = [1, 2, 3, 4, 5, 6, 7, 8]

scores = list()

for year in years:

# 前向验证

history = [x for x in train]

predictions = list()

for i in range(len(test)):

# 收集观测值

obs = list()

for y in range(1, year+1):

obs.append(history[-(y*365)])

# 进行预测

yhat = mean(obs)

predictions.append(yhat)

# 观测

history.append(test[i])

# 报告性能

rmse = sqrt(mean_squared_error(test, predictions))

scores.append(rmse)

print('Years=%d, RMSE: %.3f' % (year, rmse))

pyplot.plot(years, scores)

pyplot.show()

运行示例会打印滑动窗口的大小和相应的模型误差。

与前两种情况不同，我们可以看到随着窗口大小的增加，技能持续提高。

最佳结果是使用所有 8 年历史数据的滑动窗口，RMSE 为 4.271。

Years=1, RMSE: 5.950
Years=2, RMSE: 5.083
Years=3, RMSE: 4.664
Years=4, RMSE: 4.539
Years=5, RMSE: 4.448
Years=6, RMSE: 4.358
Years=7, RMSE: 4.371
Years=8, RMSE: 4.271

Years=1, RMSE: 5.950

Years=2, RMSE: 5.083

Years=3, RMSE: 4.664

Years=4, RMSE: 4.539

Years=5, RMSE: 4.448

Years=6, RMSE: 4.358

Years=7, RMSE: 4.371

Years=8, RMSE: 4.271

滑动窗口大小与模型误差的图使这种趋势显而易见。

这表明，如果最优模型是先前年份同一天的观测值的函数，那么获取更多历史数据可能会有用。

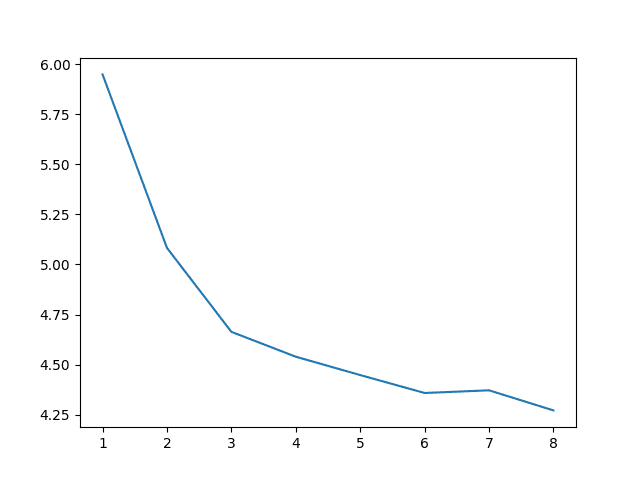
Sliding Window Size to RMSE for Daily Melbourne Maximum Temperature

每日墨尔本最高温度的滑动窗口大小与 RMSE

我们也可以通过平均先前季节的同一周或同一月来获得相似的结果，这可能会证明是一个有益的实验。

总结

在本教程中，您了解了用于时间序列预测的季节性持续性。

您学到了

如何使用先前季节的定点观测值进行持续性预测。
如何使用多个先前季节的滑动窗口的平均值进行持续性预测。
如何将季节性持续性应用于日度和月度时间序列数据。

您对季节性数据持续性有任何疑问吗？
在评论中提出您的问题，我将尽力回答。

关于此主题的更多信息

简单时间序列预测模型测试，以免误导自己

使用 Python 中的长短期记忆网络进行时间序列预测

22 条对Python 季节性持续性预测的回复

x 2017年4月7日 4:31 am #

第一个示例 – history.append(test[i])，您在循环中修改了 history 列表。这是一种糟糕的编码方式。相反，您应该操作索引。

回复
- x 2017年4月7日 4:45 am #
  
  而且您的程序不正确。这是正确的版本
  
  from pandas import Series
  from sklearn.metrics import mean_squared_error
  from math import sqrt
  from numpy import mean
  from matplotlib import pyplot
  # 加载数据
  series = Series.from_csv(‘car-sales.csv’, header=0)
  # 准备数据
  X = series.values
  train, test = X[0:-24], X[-24:]
  # 评估不同年数的平均值
  years = [1, 2, 3, 4, 5]
  scores = list()
  for year in years
  # 步进验证
  predictions = list()
  for i in range(len(test))
  # 收集观测值
  obs = list()
  for y in range(1, year+1)
  obs.append(train[-y*12 + i])
  # 进行预测
  yhat = mean(obs)
  predictions.append(yhat)
  
  # 报告表现
  rmse = sqrt(mean_squared_error(test, predictions))
  scores.append(rmse)
  print(‘Years=%d, RMSE: %.3f’ % (year, rmse))
  pyplot.plot(years, scores)
  pyplot.show()
  
  回复
  - Jason Brownlee 2017年4月9日 2:48 pm #
    
    您能否详细说明您认为发现并修复的错误？
    
    回复
- Jason Brownlee 2017年4月9日 2:47 pm #
  
  我不同意。这是演示前向验证的一种好方法。
  
  回复
x 2017年4月7日 4:48 am #

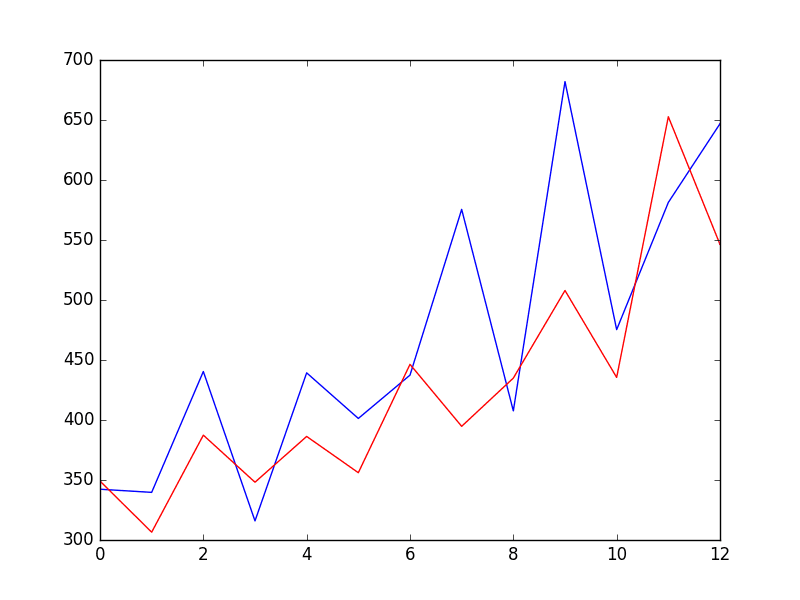
使用 5 年数据的准确性最差，正如您打印的第一个示例图所示，这没有意义。

回复
- Jason Brownlee 2017年4月9日 2:48 pm #
  
  我认为您误读了示例。
  
  我们使用 RMSE 而不是准确性，并且 RMSE 在最多历史数据时是最佳的（最低）。
  
  回复
Jordan W. 2017年4月7日 3:22 pm #

感谢本教程，并将其与之前的帖子中的数据模型联系起来。提供了一种使用滑动窗口评估季节性持续性的方法，然后绘制结果是太棒了！

我真的很喜欢“引言、测试框架、案例研究和摘要”的格式。它帮助我与数据集建立真实的联系。

我非常感谢您的网站。

回复
- Jason Brownlee 2017年4月9日 2:52 pm #
  
  谢谢 Jordan，我很高兴听到这个。
  
  回复
Jiyang Wang 2017年10月24日 2:22 am #

首先，我从您的教程中学到了很多。我想说“谢谢”。

至于本教程中的示例，早在四月份就有“x”发表了评论，但他没有详细说明他认为程序在哪里出错，尽管受到了请求。我认为错误在于第一个示例的完整代码的第 22 行

obs.append(history[-(y*12)])

我认为这一行应该是

obs.append(history[-(y*12 + i)])

因为我们想收集代表 y 的过去几年的第 i 个月的数值。

所有其他示例似乎都有同样的问题。

回复
- Jason Brownlee 2017年10月24日 5:36 am #
  
  谢谢您的留言。
  
  回复
  - Scott K 2019年2月22日 11:46 am #
    
    我也被这个卡住了。Jason 的代码是正确的。您不需要 obs.append(history[-(y*12 + i)]) 的原因是他正在用 test[i] 附加 history。
    
    回复
    - Jason Brownlee 2019年2月22日 2:46 pm #
      
      谢谢 Scott。
      
      回复
Piyasi Choudhury 2018年6月12日 5:06 am #

@ Jason 感谢如此详细的模型演练。非常有帮助且易于理解。

一个问题——我如何使用这种季节性方法来为多步预测（即不属于输入数据的一部分）生成预测……假设我想用它来生成接下来的 12 个数据点……。

非常感谢

回复
- Jason Brownlee 2018 年 6 月 12 日上午 6:49 #
  
  您可以逐歩向前推进该方法，甚至根据需要使用预测作为观测值。
  
  回复
Piyasi Choudhury 2018 年 6 月 12 日上午 10:45 #

@ Jason，关于我之前的笔记，不用管了……那是个愚蠢的问题……我自己能做到 🙂

回复
- Jason Brownlee 2018 年 6 月 12 日下午 2:26 #
  
  不客气。
  
  回复
Goddy 2019 年 9 月 17 日晚上 10:17 #

你好 Jason，

我未来的工作是预测未来一年（或多年）的天气。目前我了解了一些时间序列模型，如 ARIMA、MA 和 AR 模型，还有其他可以用于该领域的数值天气预报模型，如 ETS。

我的第一个问题是，您是否知道过去和现在用于天气预报的“经典”模型？提前感谢您的时间和回复。

我还想知道您的时间序列电子书是否有纸质版。顺便问一下，电子书是免费的吗？我在网上看到售价 37 美元。是电子书的价格还是纸质书（如果有的）的价格？

此致

Goddy

回复
- Jason Brownlee 2019 年 9 月 18 日上午 6:07 #
  
  我建议您在您的数据集上测试一系列不同的模型，看看哪种最适合您的特定数据集。
  
  抱歉，我只销售电子书，没有纸质版。
  
  您可以在此处访问我最好的免费时间序列教程。
  https://machinelearning.org.cn/start-here/#timeseries
  
  回复
  - Goddy 2019 年 9 月 19 日下午 5:51 #
    
    非常感谢您的快速回复。另外，正如我之前所说，我最近读到 ARIMA 模型可用于预测。
    
    我想问您是否知道任何“经典”（通常在不同国家用于预测天气的标准模型）的预测天气模型。谢谢！
    
    提前感谢您的回复
    
    回复
    - Jason Brownlee 2019 年 9 月 20 日上午 5:36 #
      
      我相信他们运行的是物理过程模拟，而不是线性预测模型。
      
      回复
Amelia 2019 年 10 月 28 日下午 3:30 #

非常有用的帖子！我只有一个后续问题——如果预测值等于多个先前季节的滑动窗口的平均值，如何计算预测值的 95% 置信区间？请注意，我正在处理月度数据。提前感谢您的帮助。

回复
- Jason Brownlee 2019 年 10 月 29 日上午 5:20 #
  
  也许是滑动窗口标准差的 2 倍？
  https://en.wikipedia.org/wiki/68%E2%80%9395%E2%80%9399.7_rule
  
  回复

导航

使用 Python 进行季节性持续性预测

季节性持续性

滑动窗口季节性持续性

停止以慢速学习时间序列预测！

实验测试框架

案例研究 1：月度汽车销售数据集

案例研究 2：月度书写纸销售数据集

案例研究 3：每日墨尔本最高温度数据集

总结

想用Python开发时间序列预测吗？

几分钟内开发您自己的预测

最终将时间序列预测带入
您自己的项目

关于此主题的更多信息

22 条对Python 季节性持续性预测的回复

留下回复点击此处取消回复。

导航

季节性持续性

滑动窗口季节性持续性

停止以**慢速**学习时间序列预测！

实验测试框架

案例研究 1：月度汽车销售数据集

案例研究 2：月度书写纸销售数据集

案例研究 3：每日墨尔本最高温度数据集

总结

想用Python开发时间序列预测吗？

几分钟内开发您自己的预测

最终将时间序列预测带入您自己的项目

关于此主题的更多信息

22 条对Python 季节性持续性预测的回复

留下回复 点击此处取消回复。

停止以慢速学习时间序列预测！

最终将时间序列预测带入
您自己的项目

留下回复点击此处取消回复。