使用 Python 中的 ARIMA 进行历史大小对预测技能的敏感性分析

作者： Jason Brownlee 发布于 2020 年 12 月 10 日在时间序列 21

时间序列预测模型需要多少历史数据？

这是一个具体问题，我们可以通过设计实验来研究。

在本教程中，您将了解历史数据量对 Python 中 ARIMA 预测模型技能的影响。

具体来说，在本教程中，您将：

加载标准数据集并拟合 ARIMA 模型。
设计并执行历史数据年限对模型技能的敏感度分析。
分析敏感度分析的结果。

这将为您自己的时间序列预测问题提供一个执行类似历史数据集大小敏感度分析的模板。

通过我的新书《使用 Python 进行时间序列预测》启动您的项目，其中包括分步教程和所有示例的 Python 源代码文件。

让我们开始吧。

2017 年 8 月更新：修复了一个错误，该错误导致模型在原始数据而不是季节性差分数据上构建。感谢 David Ravnsborg！
2018 年 6 月更新：删除了重复的句子。感谢 Rahul！
2019 年 4 月更新：更新了数据集链接。
2019年8月更新：更新了数据加载以使用新的API。
2020 年 12 月更新：将 ARIMA API 更新为最新版本的 statsmodels。

Sensitivity Analysis of History Size to Forecast Skill with ARIMA in Python

使用 Python 中的 ARIMA 进行历史大小对预测技能的敏感性分析
图片来源：Sean MacEntee，部分权利保留。

日最低气温数据集

该数据集描述了澳大利亚墨尔本市 10 年（1981-1990 年）的每日最低气温。

单位是摄氏度，共有3650个观测值。数据来源归功于澳大利亚气象局。

下载数据集并将其保存到当前工作目录中，文件名为“daily-minimum-temperatures.csv”。

下载数据集

下面的示例将数据集加载为 Pandas Series。

# 时间序列的折线图

from pandas import read_csv

from matplotlib import pyplot

# 加载数据集

series = read_csv('daily-minimum-temperatures.csv', header=0, index_col=0)

# 显示前几行

print(series.head(20))

# 数据集的折线图

series.plot()

pyplot.show()

运行示例会打印加载文件的前 20 行。

日期

1981-01-01 20.7

1981-01-02 17.9

1981-01-03 18.8

1981-01-04 14.6

1981-01-05 15.8

1981-01-06 15.8

1981-01-07 15.8

1981-01-08 17.4

1981-01-09 21.8

1981-01-10 20.0

1981-01-11 16.2

1981-01-12 13.3

1981-01-13 16.7

1981-01-14 21.5

1981-01-15 25.0

1981-01-16 20.7

1981-01-17 20.6

1981-01-18 24.8

1981-01-19 17.7

1981-01-20 15.5

名称：温度，数据类型：float64

然后数据被绘制成线图，显示季节性模式。

Minimum Daily Temperatures Dataset Line Plot

每日最低气温数据集线图

ARIMA 预测模型

在本节中，我们将为数据拟合一个 ARIMA 预测模型。

模型的参数将不会进行调整，但会具有熟练性。

数据包含一个一年期的季节性分量，必须将其移除才能使数据平稳并适合与 ARIMA 模型一起使用。

我们可以通过减去一年前（365 天）的观测值来计算季节性差分。这很粗糙，因为它没有考虑闰年。这也意味着第一年的数据将无法用于建模，因为一年前没有数据可以进行差分。

# 季节性差分

differenced = series.diff(365)

# 截去第一年的空数据

differenced = differenced[365:]

我们将为数据拟合一个 ARIMA(7,0,0) 模型并打印摘要信息。这表明模型是稳定的。

# 拟合模型

model = ARIMA(differenced, order=(7,0,0))

model_fit = model.fit()

print(model_fit.summary())

综上所述，完整的示例代码如下。

# 拟合 ARIMA 模型

from pandas import read_csv

from matplotlib import pyplot

from statsmodels.tsa.arima.model import ARIMA

# 加载数据集

series = read_csv('daily-minimum-temperatures.csv', header=0, index_col=0)

# 季节性差分

differenced = series.diff(365)

# 截去第一年的空数据

differenced = series[365:]

# 拟合模型

model = ARIMA(differenced, order=(7,0,0))

model_fit = model.fit()

print(model_fit.summary())

运行示例会提供拟合的 ARIMA 模型的摘要。

ARMA Model Results                              
==============================================================================
Dep. Variable:                   Temp   No. Observations:                 3285
Model:                     ARMA(7, 0)   Log Likelihood               -8690.089
Method:                       css-mle   S.D. of innovations              3.409
Date:                Fri, 25 Aug 2017   AIC                          17396.178
Time:                        15:02:59   BIC                          17444.955
Sample:                    01-01-1982   HQIC                         17413.643
                         - 12-31-1990                                         
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
ar.L1.Temp     0.5278      0.017     30.264      0.000       0.494       0.562
ar.L2.Temp    -0.1099      0.020     -5.576      0.000      -0.149      -0.071
ar.L3.Temp     0.0286      0.020      1.441      0.150      -0.010       0.067
ar.L4.Temp     0.0307      0.020      1.549      0.122      -0.008       0.070
ar.L5.Temp     0.0090      0.020      0.456      0.648      -0.030       0.048
ar.L6.Temp     0.0164      0.020      0.830      0.407      -0.022       0.055
ar.L7.Temp     0.0272      0.017      1.557      0.120      -0.007       0.061
                                    Roots                                    
=============================================================================
                 Real           Imaginary           Modulus         Frequency
-----------------------------------------------------------------------------
AR.1            1.3305           -0.0000j            1.3305           -0.0000
AR.2            0.9936           -1.1966j            1.5553           -0.1397
AR.3            0.9936           +1.1966j            1.5553            0.1397
AR.4           -0.2067           -1.7061j            1.7186           -0.2692
AR.5           -0.2067           +1.7061j            1.7186            0.2692
AR.6           -1.7536           -0.8938j            1.9683           -0.4250
AR.7           -1.7536           +0.8938j            1.9683            0.4250
-----------------------------------------------------------------------------

ARMA 模型结果

==============================================================================

因变量：温度观测数量： 3285

模型： ARMA(7, 0) 对数似然 -8690.089

方法： css-mle 创新标准差 3.409

日期： 2017 年 8 月 25 日星期五 AIC 17396.178

时间： 15:02:59 BIC 17444.955

样本： 1982-01-01 HQIC 17413.643

- 12-31-1990

==============================================================================

系数标准误差 z P>|z| [0.025 0.975]

------------------------------------------------------------------------------

ar.L1.Temp 0.5278 0.017 30.264 0.000 0.494 0.562

ar.L2.Temp -0.1099 0.020 -5.576 0.000 -0.149 -0.071

ar.L3.Temp 0.0286 0.020 1.441 0.150 -0.010 0.067

ar.L4.Temp 0.0307 0.020 1.549 0.122 -0.008 0.070

ar.L5.Temp 0.0090 0.020 0.456 0.648 -0.030 0.048

ar.L6.Temp 0.0164 0.020 0.830 0.407 -0.022 0.055

ar.L7.Temp 0.0272 0.017 1.557 0.120 -0.007 0.061

根

=============================================================================

实数虚数模数频率

-----------------------------------------------------------------------------

AR.1 1.3305 -0.0000j 1.3305 -0.0000

AR.2 0.9936 -1.1966j 1.5553 -0.1397

AR.3 0.9936 +1.1966j 1.5553 0.1397

AR.4 -0.2067 -1.7061j 1.7186 -0.2692

AR.5 -0.2067 +1.7061j 1.7186 0.2692

AR.6 -1.7536 -0.8938j 1.9683 -0.4250

AR.7 -1.7536 +0.8938j 1.9683 0.4250

-----------------------------------------------------------------------------

模型历史敏感度分析

在本节中，我们将探讨历史数据量对拟合模型技能的影响。

原始数据有 10 年的数据。季节性差分后，我们剩下 9 年的数据。我们将最后一年数据保留作为测试数据，并在这最后一年中执行滚动预测验证。

将收集逐日预测结果，并计算均方根误差 (RMSE) 分数，以指示模型的技能。

以下代码片段将季节性调整后的数据分为训练集和测试集。

1	train, test = differenced[differenced.index < '1990'], differenced['1990']

选择适合您自己的预测问题的时间间隔非常重要。

我们将评估模型使用过去 1 年数据、然后 2 年数据（一直追溯到 8 年可用历史数据）的技能。

考虑到数据的季节性，一年是测试此数据集的良好时间间隔，但也可以测试其他间隔，例如按月或多年间隔。

以下代码片段显示了我们如何按年份向后逐步选择所有可用观测值。

例如

测试 1：1989 年所有数据
测试 2：1988 年至 1989 年所有数据

等等。

# 划分

train, test = differenced[differenced.index < '1990'], differenced['1990']

years = ['1989', '1988', '1987', '1986', '1985', '1984', '1983', '1982']

for year in years:

# 从“年份”累积选择到 1989 年的数据

dataset = train[train.index >= year]

下一步是评估 ARIMA 模型。

我们将使用滚动预测验证。这意味着将根据选定的历史数据构建模型，并预测下一个时间步（1990 年 1 月 1 日）。该时间步的实际观测值将添加到历史数据中，然后构建新模型，并预测下一个时间步。

预测结果将被收集并与最后一年的观测值进行比较，以得出误差分数。在这种情况下，将使用 RMSE 作为分数，并且将与观测值本身处于相同的尺度。

# 遍历测试集中的时间步

values = dataset.values

history = [values[i] for i in range(len(values))]

predictions = list()

test_values = test.values

for t in range(len(test_values)):

# 拟合模型

model = ARIMA(history, order=(7,0,0))

model_fit = model.fit()

# 进行预测

yhat = model_fit.forecast()[0]

predictions.append(yhat)

history.append(test_values[t])

rmse = sqrt(mean_squared_error(test_values, predictions))

print('%s-%s (%d values) RMSE: %.3f' % (years[0], year, len(values), rmse))

综上所述，完整的示例代码如下。

# fit an ARIMA model
from pandas import read_csv
from matplotlib import pyplot
from statsmodels.tsa.arima.model import ARIMA
from sklearn.metrics import mean_squared_error
from math import sqrt
# load dataset
series = read_csv('daily-minimum-temperatures.csv', header=0, index_col=0)
# seasonal difference
differenced = series.diff(365)
# trim off the first year of empty data
differenced = differenced[365:]
# split
train, test = differenced[differenced.index < '1990'], differenced['1990']
years = ['1989', '1988', '1987', '1986', '1985', '1984', '1983', '1982']
for year in years:
	# select data from 'year' cumulative to 1989
	dataset = train[train.index >= year]
	# walk forward over time steps in test
	values = dataset.values
	history = [values[i] for i in range(len(values))]
	predictions = list()
	test_values = test.values
	for t in range(len(test_values)):
		# fit model
		model = ARIMA(history, order=(7,0,0))
		model_fit = model.fit()
		# make prediction
		yhat = model_fit.forecast()[0]
		predictions.append(yhat)
		history.append(test_values[t])
	rmse = sqrt(mean_squared_error(test_values, predictions))
	print('%s-%s (%d values) RMSE: %.3f' % (years[0], year, len(values), rmse))

# 拟合 ARIMA 模型

from pandas import read_csv

from matplotlib import pyplot

from statsmodels.tsa.arima.model import ARIMA

from sklearn.metrics import mean_squared_error

from math import sqrt

# 加载数据集

series = read_csv('daily-minimum-temperatures.csv', header=0, index_col=0)

# 季节性差分

differenced = series.diff(365)

# 截去第一年的空数据

differenced = differenced[365:]

# 划分

train, test = differenced[differenced.index < '1990'], differenced['1990']

years = ['1989', '1988', '1987', '1986', '1985', '1984', '1983', '1982']

for year in years:

# 从“年份”累积选择到 1989 年的数据

dataset = train[train.index >= year]

# 在测试中的时间步上滚动向前

values = dataset.values

history = [values[i] for i in range(len(values))]

predictions = list()

test_values = test.values

for t in range(len(test_values)):

# 拟合模型

model = ARIMA(history, order=(7,0,0))

model_fit = model.fit()

# 进行预测

yhat = model_fit.forecast()[0]

predictions.append(yhat)

history.append(test_values[t])

rmse = sqrt(mean_squared_error(test_values, predictions))

print('%s-%s (%d values) RMSE: %.3f' % (years[0], year, len(values), rmse))

运行示例会打印历史数据的时间间隔、历史数据中的观测值数量以及使用该历史数据训练的模型的 RMSE 技能。

该示例需要一段时间才能运行，因为为每个历史训练数据的累积间隔创建了 365 个 ARIMA 模型。

1989-1989（365 个值）RMSE：3.120

1989-1988（730 个值）RMSE：3.109

1989-1987（1095 个值）RMSE：3.104

1989-1986（1460 个值）RMSE：3.108

1989-1985（1825 个值）RMSE：3.107

1989-1984（2190 个值）RMSE：3.103

1989-1983（2555 个值）RMSE：3.099

1989-1982（2920 个值）RMSE：3.096

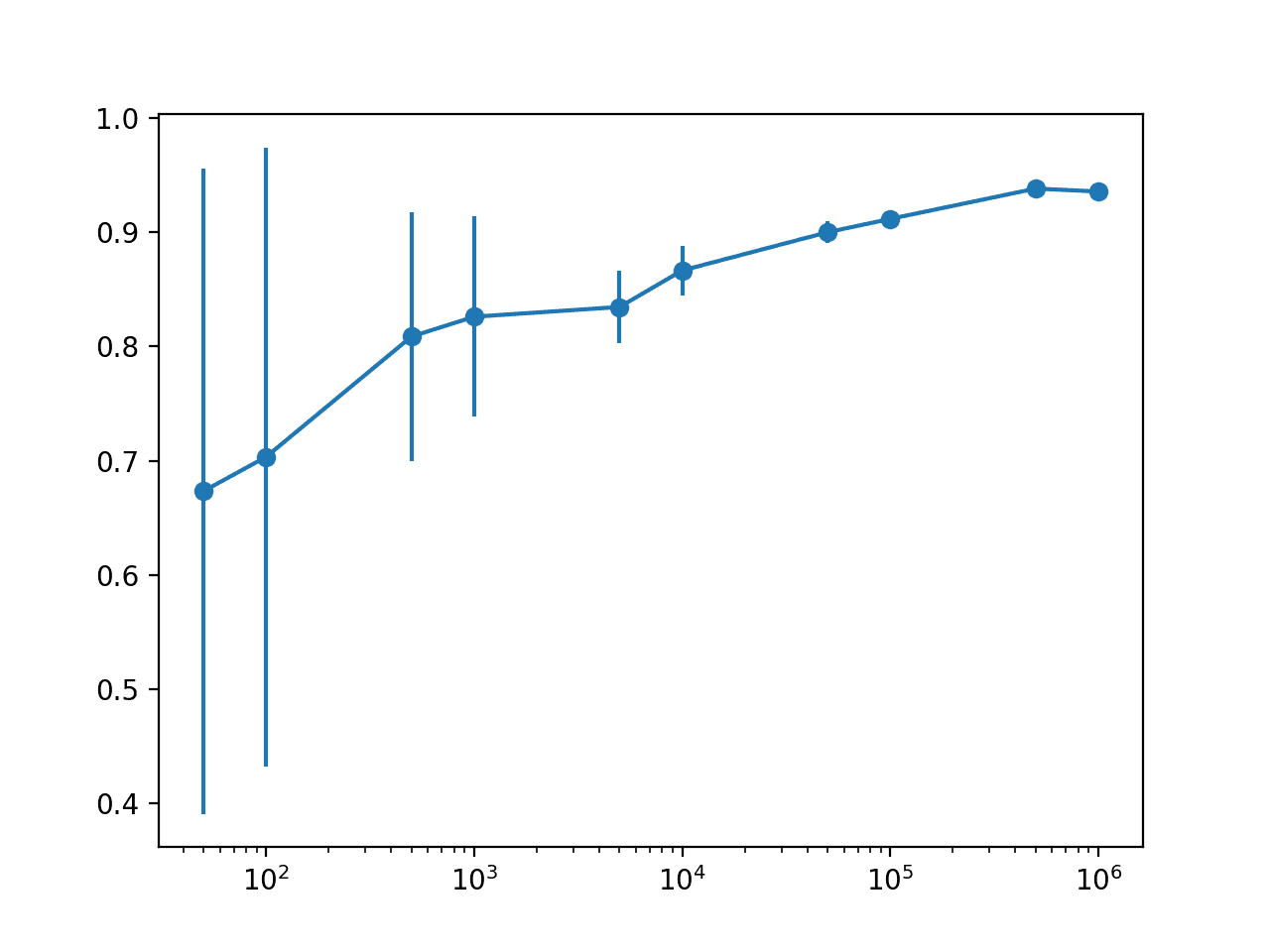
结果表明，随着可用历史数据量的增加，模型误差会减小，但趋势并非纯线性。

我们确实看到在 2-3 年时可能存在边际收益递减点。了解您可以使用更少年的数据在数据可用性或模型训练时间长是问题所在的领域中非常有用。

我们可以绘制 ARIMA 模型误差与训练观测值数量之间的关系。

from matplotlib import pyplot

x = [365, 730, 1095, 1460, 1825, 2190, 2555, 2920]

y = [3.120, 3.109, 3.104, 3.108, 3.107, 3.103, 3.099, 3.096]

pyplot.plot(x, y)

pyplot.show()

运行示例会创建一个图表，该图表几乎显示了随着训练样本的增加，误差呈线性下降趋势。

历史数据量与 ARIMA 模型误差

这通常是预料之中的，因为更多的历史数据意味着系数可以更好地优化，以描述多年数据的变异性，这在很大程度上是如此。

也有一个反直觉。人们可能期望模型性能随着历史数据的增多而提高，因为最近几年的数据可能与明年数据更相似。这种直觉在概念漂移较大的领域中可能更有效。

扩展

本节讨论了敏感度分析的局限性和扩展。

未调优模型。示例中使用的 ARIMA 模型绝不是针对问题进行调优的。理想情况下，训练历史数据量敏感度分析应使用已调优的 ARIMA 模型或针对每种情况进行调优的模型来执行。
统计显著性。目前尚不清楚模型技能的差异是否具有统计显著性。可以使用配对统计显著性检验来辨别 RMSE 的差异是否具有实际意义。
替代模型。ARIMA 使用历史数据来拟合系数。其他模型可能以其他方式使用不断增加的历史数据。可以研究其他非线性机器学习模型。
替代时间间隔。选择了年份来连接历史数据，但可以使用其他时间间隔。对于此数据集，在一个或两年历史数据中，周或月可能是一个很好的时间间隔，因为极近期的历史数据可能会以有用的方式偏置系数。

总结

在本教程中，您学习了如何设计、执行和分析时间序列预测模型所用历史数据量的敏感度分析。

你有什么问题吗？
在评论中提出您的问题，我会尽力回答。

关于此主题的更多信息

如何使用 Python 中的 ARIMA 进行样本外预测

使用 Python 进行时间序列预测的特征选择

《Python 中 ARIMA 模型历史数据量对预测技能的敏感度分析》的 21 条回复

sura 2017 年 4 月 7 日上午 3:39 #

谢谢！但是，您可以给我一个数据集的下载地址吗？我想再试一次！
谢谢！

回复
- Jason Brownlee 2017 年 4 月 9 日下午 2:46 #
  
  抱歉，在这里
  https://datamarket.com/data/set/2324/daily-minimum-temperatures-in-melbourne-australia-1981-1990
  
  回复
Eugeniy 2017 年 5 月 5 日下午 6:44 #

下午好！
谢谢您的文章。
请问，是否有更正式和数学化的历史数据量对预测敏感度分析的定义？
或者这通常只是一种实验性的确定方法？
谢谢！

回复
- Jason Brownlee 2017 年 5 月 6 日上午 7:40 #
  
  我相信您可以分析历史数据量对模型的分析影响。
  
  敏感度分析旨在通过经验方式回答这个问题。
  
  回复
David Ravnsborg 2017 年 8 月 18 日上午 9:36 #

你为什么要声明“differenced”，然后立即覆盖它而不使用它？

回复
- Jason Brownlee 2017 年 8 月 18 日下午 4:37 #
  
  好问题，这对我来说像个 bug。我会添加到 Trello 备忘录中进行修复。
  
  回复
  - David Ravnsborg 2017 年 8 月 18 日下午 5:48 #
    
    我在我这边进一步研究了一下。我认为这只是一个打字错误，其中
    # 季节性差分
    differenced = series.diff(365)
    # 截去第一年的空数据
    differenced = series[365:]
    
    应该改成...
    
    # 季节性差分
    differenced = series.diff(365)
    # 截去第一年的空数据
    differenced = differenced[365:]
    
    但这完全改变了结果，而且变得更糟 🙁 你能涵盖这一点吗？这将是一个很棒的后续。这是我得到的结果
    model.py:496: ConvergenceWarning: 最大似然优化未能收敛。检查 mle_retvals
    “检查 mle_retvals”，ConvergenceWarning)
    1989-1989（365 个值）RMSE：3.120
    1989-1988（730 个值）RMSE：3.109
    model.py:496: ConvergenceWarning: 最大似然优化未能收敛。检查 mle_retvals
    “检查 mle_retvals”，ConvergenceWarning)
    1989-1987（1095 个值）RMSE：3.104
    1989-1986（1460 个值）RMSE：3.108
    1989-1985（1825 个值）RMSE：3.107
    model.py:496: ConvergenceWarning: 最大似然优化未能收敛。检查 mle_retvals
    “检查 mle_retvals”，ConvergenceWarning)
    1989-1984（2190 个值）RMSE：3.103
    1989-1983（2555 个值）RMSE：3.099
    1989-1982（2920 个值）RMSE：3.096
    
    回复
    - Jason Brownlee 2017 年 8 月 25 日下午 3:15 #
      
      我已经更新了帖子，再次感谢 David。
      
      我们仍然看到相同的线性下降误差趋势。
      
      请记住，RMSE 分数实际上是以季节性差分温度为单位的。这可能会产生影响。
      
      如果您对更好的结果感兴趣，可以尝试对 ARIMA 参数进行网格搜索，看看我们是否能做得比 ARIMA(7,0,0) 更好，或者执行季节性差分是否能在此问题上产生更好的最终 RMSE。
      
      回复
Rahul 2018 年 6 月 11 日下午 7:04 #

嗨，Jason，

只是一个小小的修改。

Ctrl+F “逐日预测将被收集并计算均方根” 这句话重复了两次。这不是问题，但我想让您知道。

很棒的文章，我真的很喜欢阅读您的作品 🙂

回复
- Jason Brownlee 2018 年 6 月 12 日上午 6:38 #
  
  谢谢，已修正。
  
  回复
Raghu 2018 年 10 月 13 日上午 1:16 #

我使用增广迪基-富勒方法对提供的数据集进行了平稳性检验，结果如下：
检验统计量 -4.445747
p 值 0.000246
使用的滞后数 20.000000
使用的观测值数量 3629.000000
临界值 (1%) -3.432153
临界值 (5%) -2.862337
临界值 (10%) -2.567194

根据结果，我得出结论，数据看起来非常平稳
我有一个问题，即使数据是平稳的，你为什么要应用季节性差分？

回复
- Jason Brownlee 2018 年 10 月 13 日上午 6:15 #
  
  你具体评估了哪个数据集？
  
  温度数据集明显具有时间依赖结构。
  
  回复
  - Raghu 2018 年 10 月 15 日下午 7:24 #
    
    我评估了“daily-minimum-temperatures.csv”数据集（本文中使用的数据集）。
    但 ADF 结果（在上一条评论中复制）显示数据看起来是平稳的。
    
    回复
lalitha bharathula 2018 年 12 月 27 日晚上 10:24 #

假设我想根据日期和当天温度（基于温度，如太冷会影响我的销售额）预测某个地区的销售额。请告诉我这里是否可以使用 ARIMA。

回复
- Jason Brownlee 2018 年 12 月 28 日上午 5:57 #
  
  也许可以尝试一下，看看效果如何。
  
  回复
Btran 2019 年 5 月 27 日下午 7:38 #

嗨，谢谢您的博客。我是新手，抱歉英语不好，您能解释一下 ARIMA 模型结果中的值吗，我不知道 AIC、BIC、HQIC 和 coef、std err、z、P>|z|……这些值是什么意思？以及如何判断它是一个好的结果？

回复
- Jason Brownlee 2019 年 5 月 28 日上午 8:12 #
  
  好问题，这可能会有所帮助
  https://machinelearning.org.cn/faq/single-faq/how-to-know-if-a-model-has-good-performance
  
  回复
Ed 2019 年 11 月 30 日上午 3:38 #

很棒的教程！关于方法论有一个问题——您提到“我们可以按年倒退并累积选择所有可用观测值”。是否有理由倒退（从 1989 年到 1982 年），而不是前进（从 1982 年到 1989 年，例如（测试 1）1982 年所有数据，（测试 2）测试 2：1982 年到 1983 年所有数据，等等）？

回复
- Jason Brownlee 2019 年 11 月 30 日上午 6:31 #
  
  谢谢。
  
  我们在评估时向前推进，我是在解释如何扩展窗口。抱歉造成了困惑。
  
  回复
Diego 2021年2月25日晚上9:39 #

你好，Jason。

你们有在时间序列中使用对数函数的例子吗？

回复
- Jason Brownlee 2021年2月26日上午4:58 #
  
  是的，就在这里。
  https://machinelearning.org.cn/power-transform-time-series-forecast-data-python/
  
  回复

导航

使用 Python 中的 ARIMA 进行历史大小对预测技能的敏感性分析

日最低气温数据集

ARIMA 预测模型

模型历史敏感度分析

扩展

总结

想用Python开发时间序列预测吗？

几分钟内开发您自己的预测

最终将时间序列预测带入
您自己的项目

关于此主题的更多信息

《Python 中 ARIMA 模型历史数据量对预测技能的敏感度分析》的 21 条回复

发表评论点击此处取消回复。

导航

日最低气温数据集

ARIMA 预测模型

模型历史敏感度分析

扩展

总结

想用Python开发时间序列预测吗？

几分钟内开发您自己的预测

最终将时间序列预测带入您自己的项目

关于此主题的更多信息

《Python 中 ARIMA 模型历史数据量对预测技能的敏感度分析》的 21 条回复

发表评论 点击此处取消回复。

最终将时间序列预测带入
您自己的项目

发表评论点击此处取消回复。