机器学习简单线性回归教程

线性回归是一种非常简单但已被证明对许多情况都非常有用。

在本帖中，您将逐步了解线性回归的工作原理。阅读本帖后，您将了解

• 如何一步一步计算简单线性回归。
• 如何使用电子表格执行所有计算。
• 如何使用模型对新数据进行预测。
• 大大简化计算的快捷方式。

本教程是为开发人员编写的，不假定您有任何数学或统计学背景。

本教程的目的是让您在自己的电子表格中进行学习，这将有助于巩固概念。

通过我的新书《机器学习算法精通》启动您的项目，其中包含分步教程和所有示例的Excel电子表格文件。

让我们开始吧。

更新#1：修复了 RMSE 计算中的一个错误。

机器学习简单线性回归教程
照片由Catface27拍摄，保留部分权利。

教程数据集

我们使用的数据集是完全虚构的。

以下是原始数据。

属性 x 是输入变量，y 是我们试图预测的输出变量。如果我们获得更多数据，我们将只有 x 值，而会关注预测 y 值。

以下是 x 与 y 的简单散点图。

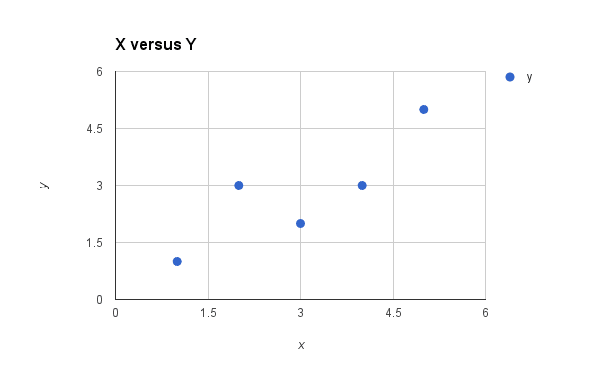
用于简单线性回归的数据集图

我们可以看到 x 和 y 之间的关系看起来有点线性。也就是说，我们可能可以在图的左下角到右上角画一条对角线来大致描述数据之间的关系。

这表明对这个小型数据集使用线性回归可能是合适的。

获取您的免费算法思维导图

方便的机器学习算法思维导图样本。

我创建了一份方便的思维导图，其中包含60多种按类型组织的算法。

下载、打印并使用它。

简单线性回归

当我们只有一个输入属性 (x) 并想使用线性回归时，这被称为简单线性回归。

如果我们有多个输入属性（例如 x1、x2、x3 等），这被称为多元线性回归。线性回归的步骤与多元线性回归不同，且更简单，因此这是一个很好的起点。

在本节中，我们将根据训练数据创建一个简单线性回归模型，然后对训练数据进行预测，以了解模型对数据的关系学习得如何。

使用简单线性回归，我们希望模型如下所示

y = B0 + B1 * x

这是一个直线，其中 y 是我们想要预测的输出变量，x 是我们已知的输入变量，B0 和 B1 是我们需要估计的系数，它们可以移动直线。

技术上讲，B0 被称为截距，因为它决定了直线在 y 轴上的截距。在机器学习中，我们可以称之为偏差，因为它被加到所有预测中以进行偏移。B1 项被称为斜率，因为它定义了直线的斜率，或者 x 在我们添加偏差之前如何转换为 y 值。

目标是找到最佳的系数估计值，以最小化从 x 预测 y 的误差。

简单回归很棒，因为我们不必通过试错来寻找值，也不必使用更高级的线性代数来解析计算它们，而是可以直接从数据中估计它们。

我们可以开始估计 B1 的值

B1 = sum((xi-mean(x)) * (yi-mean(y))) / sum((xi – mean(x))^2)

其中 mean() 是我们数据集中变量的平均值。xi 和 yi 指的是我们需要对数据集中的所有值重复这些计算，而 i 指的是 x 或 y 的第 i 个值。

我们可以使用 B1 和我们数据集的一些统计数据来计算 B0，如下所示

B0 = mean(y) – B1 * mean(x)

不算太难吧？我们可以在电子表格中直接计算这些。

估计斜率 (B1)

让我们从方程的顶部开始，即分子。

首先，我们需要计算 x 和 y 的平均值。平均值计算为

1/n * sum(x)

其中 n 是值的数量（本例中为 5）。您可以在电子表格中使用 AVERAGE() 函数。让我们计算 x 和 y 变量的平均值

mean(x) = 3

mean(y) = 2.8

现在我们需要计算每个变量与平均值的差值。我们先用 x 来做

现在我们为 y 变量也这样做

现在我们有了计算分子的部分。我们所要做的就是将每个 x 的差值与每个 y 的差值相乘，然后计算这些乘积的总和。

对最后一列求和，我们计算出的分子是 8。

现在我们需要计算 B1 方程的底部，即分母。这是通过计算每个 x 值与平均值的平方差的总和来计算的。

我们已经计算了每个 x 值与平均值的差值，我们只需要对每个值进行平方，然后计算总和。

计算这些平方值的总和得到分母 10

现在我们可以计算斜率的值了。

B1 = 8 / 10

B1 = 0.8

估计截距 (B0)

这要容易得多，因为我们已经知道所有涉及项的值。

B0 = mean(y) – B1 * mean(x)

或者

B0 = 2.8 – 0.8 * 3

或者

B0 = 0.4

很简单。

进行预测

现在我们有了简单线性回归方程的系数。

y = B0 + B1 * x

或者

y = 0.4 + 0.8 * x

让我们通过对训练数据进行预测来尝试模型。

我们可以将这些预测值与我们的数据一起绘制成一条线。这给了我们一个直观的印象，这条线在多大程度上拟合了我们的数据。

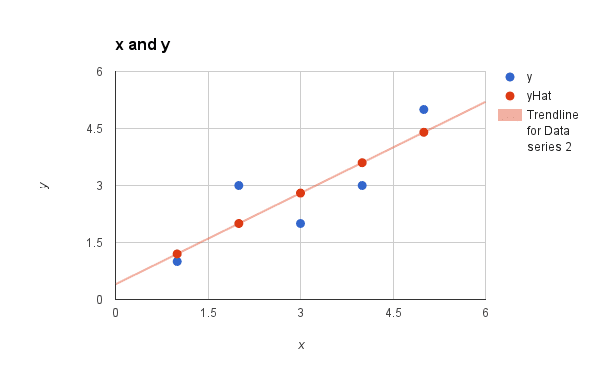
简单线性回归模型

误差估计

我们可以计算一个预测误差，称为均方根误差 (Root Mean Squared Error) 或 RMSE。

RMSE = sqrt( sum( (pi – yi)^2 )/n )

其中 sqrt() 是平方根函数，p 是预测值，y 是实际值，i 是特定实例的索引，n 是预测的数量，因为我们必须计算所有预测值的误差。

首先，我们必须计算模型预测值与实际 y 值之间的差值。

我们可以轻松计算这些误差值的平方（误差*误差或误差^2）。

这些误差的总和是 2.4 单位，除以 n 并取平方根得到

RMSE = 0.692

或者说，每次预测平均误差约为 0.692 单位。

快捷方式

在我们结束之前，我想给您展示一种快速计算系数的方法。

简单线性回归是最简单的回归形式，也是研究得最多的。有一个快捷方式，您可以使用它来快速估计 B0 和 B1 的值。

实际上，这是计算 B1 的快捷方式。B1 的计算可以重写为

B1 = corr(x, y) * stdev(y) / stdev(x)

其中 corr(x) 是 x 和 y 之间的相关性，stdev() 是变量的标准差计算。

相关性（也称为皮尔逊相关系数）是衡量两个变量在 -1 到 1 范围内的相关程度。值为 1 表示两个变量完全正相关，它们一起移动，值为 -1 表示它们完全负相关，一个移动时另一个会向相反方向移动。

标准差是衡量数据与平均值平均分散程度的指标。

您可以使用电子表格中的 PEARSON() 函数将 x 和 y 的相关性计算为 0.852（高度相关），并使用 STDEV() 函数计算 x 的标准差为 1.5811，y 的标准差为 1.4832。

将这些值代入，我们得到

B1 = 0.852 * 1.4832 / 1.5811

B1 = 0.799

与上面的 0.8 值非常接近。请注意，如果我们对电子表格中的相关性和标准差方程使用更完整的精度，我们会得到 0.8。

总结

在本帖中，您了解了如何在电子表格中逐步实现线性回归。您学到了

• 如何根据训练数据估计简单线性回归模型的系数。
• 如何使用学习到的模型进行预测。

您对这篇帖子或线性回归有任何疑问吗？请留言提问，我会尽力回答。

了解机器学习算法的工作原理！

几分钟内了解算法如何工作

...只需算术和简单示例

在我的新电子书中探索如何实现
精通机器学习算法

它涵盖了**10种顶级算法**的**解释**和**示例**，例如：
_线性回归_、_k-近邻_、_支持向量机_等等...

最后，揭开
机器学习算法的神秘面纱

跳过学术理论。只看结果。

查看内容