在时间序列预测问题上建立一个强大的基准性能非常重要,并且不要欺骗自己认为复杂的模型很有技巧,而实际上它们并非如此。
这要求您评估一套标准的朴素或简单的时序预测模型,以了解更复杂的模型需要击败的最低可接受性能。
应用这些简单的模型还可以为可能带来更好性能的更高级方法带来新的想法。
在本教程中,您将学习如何在真实数据集上实现和自动化三个标准的基准时间序列预测方法。
具体来说,您将学习
- 如何自动化持续性模型并测试一系列持续性值。
- 如何自动化扩展窗口模型。
- 如何自动化滚动窗口预测模型并测试一系列窗口大小。
这是一个重要的话题,强烈推荐用于任何时间序列预测项目。
通过我的新书《Python时间序列预测》启动您的项目,其中包括分步教程和所有示例的Python源代码文件。
让我们开始吧。
- 2019 年 4 月更新:更新了数据集链接。
- 2019年8月更新:更新了数据加载以使用新的API。
概述
本教程分为以下5部分
- 月度汽车销售数据集:对我们将使用的标准时间序列数据集的概述。
- 测试设置:本教程中我们将如何评估预测模型。
- 持续性预测:持续性预测及其自动化方法。
- 扩展窗口预测:扩展窗口预测及其自动化方法。
- 滚动窗口预测:滚动窗口预测及其自动化方法。
使用最新的Python SciPy环境,包括Python 2或3,Pandas,Numpy和Matplotlib。
月度汽车销售数据集
在本教程中,我们将使用月度汽车销售数据集。
该数据集描述了1960年至1968年间加拿大魁北克省的汽车销售数量。
单位是销售数量,共有108个观测值。原始数据归功于Abraham和Ledolter(1983)。
下载数据集并将其保存到当前工作目录,文件名为“car-sales.csv”。请注意,您可能需要从文件中删除页脚信息。
下面的代码将数据集加载为Pandas Series对象。
|
1 2 3 4 5 6 7 8 9 10 |
# 时间序列的折线图 from pandas import read_csv from matplotlib import pyplot # 加载数据集 series = read_csv('car-sales.csv', header=0, index_col=0) # 显示前几行 print(series.head(5)) # 数据集的折线图 series.plot() pyplot.show() |
运行示例将打印数据的前5行。
|
1 2 3 4 5 6 7 |
月份 1960-01-01 6550 1960-02-01 8728 1960-03-01 12026 1960-04-01 14395 1960-05-01 14587 Name: Sales, dtype: int64 |
还提供了数据的折线图。
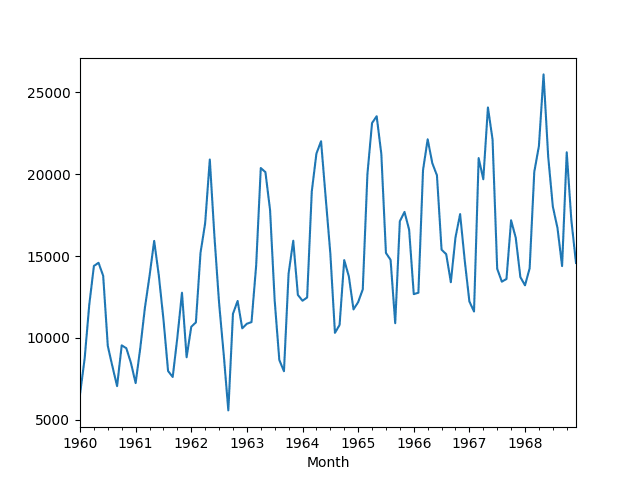
月度汽车销售数据集折线图
实验测试设置
一致地评估时间序列预测模型很重要。
在本节中,我们将定义如何评估本教程中的三个预测模型。
首先,我们将最后两年的数据保留下来,并在这些数据上评估预测。考虑到数据是月度数据,这意味着将使用最后24个观测值作为测试数据。
我们将使用前向验证方法来评估模型性能。这意味着将枚举测试数据集中的每个时间步,在历史数据上构建模型,并将预测与预期值进行比较。然后,该观测值将被添加到训练数据集中,并重复该过程。
前向验证是一种评估时间序列预测模型的现实方法,因为人们期望模型在可用新观测值时进行更新。
最后,将使用均方根误差(RMSE)来评估预测。RMSE的好处是它会惩罚较大的误差,并且得分与预测值(每月汽车销售量)的单位相同。
总之,测试框架包括
- 最后2年的数据用作测试集。
- 使用前向验证进行模型评估。
- 使用均方根误差来报告模型技能。
优化持续性预测
持续性预测涉及使用先前的观测值来预测下一个时间步。
因此,这种方法通常被称为朴素预测。
为什么只使用先前的观测值?在本节中,我们将研究如何自动化持续性预测,并评估使用任何任意先前时间步来预测下一个时间步。
我们将探索在持续性模型中使用先前24个月的每个点观测值。将使用测试框架评估每个配置,并收集RMSE得分。然后,我们将显示得分,并绘制持续时间步和模型技能之间的关系。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
from pandas import read_csv from sklearn.metrics import mean_squared_error from math import sqrt from matplotlib import pyplot # 加载数据 series = read_csv('car-sales.csv', header=0, index_col=0) # 准备数据 X = series.values train, test = X[0:-24], X[-24:] persistence_values = range(1, 25) scores = list() for p in persistence_values: # 前向验证 history = [x for x in train] predictions = list() for i in range(len(test)): # 进行预测 yhat = history[-p] predictions.append(yhat) # 观测 history.append(test[i]) # 报告性能 rmse = sqrt(mean_squared_error(test, predictions)) scores.append(rmse) print('p=%d RMSE:%.3f' % (p, rmse)) # 将得分绘制在持续性值上 pyplot.plot(persistence_values, scores) pyplot.show() |
运行示例将打印每个持续点观测值的RMSE。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
p=1 RMSE:3947.200 p=2 RMSE:5485.353 p=3 RMSE:6346.176 p=4 RMSE:6474.553 p=5 RMSE:5756.543 p=6 RMSE:5756.076 p=7 RMSE:5958.665 p=8 RMSE:6543.266 p=9 RMSE:6450.839 p=10 RMSE:5595.971 p=11 RMSE:3806.482 p=12 RMSE:1997.732 p=13 RMSE:3968.987 p=14 RMSE:5210.866 p=15 RMSE:6299.040 p=16 RMSE:6144.881 p=17 RMSE:5349.691 p=18 RMSE:5534.784 p=19 RMSE:5655.016 p=20 RMSE:6746.872 p=21 RMSE:6784.611 p=22 RMSE:5642.737 p=23 RMSE:3692.062 p=24 RMSE:2119.103 |
还将创建持续值 (t-n) 与模型技能 (RMSE) 的关系图。
从结果中可以清楚地看出,在当前数据集中,预测12个月前或24个月前的观测值是一个很好的起点。
达到的最佳结果是预测t-12的结果,RMSE为1997.732辆汽车销量。
这是显而易见的结果,但也很有用。
我们希望预测模型能够组合t-12、t-24、t-36等观测值的加权组合,这将是一个强大的起点。
这也表明,在当前数据集中,t-1的朴素预测将是一个不太理想的起点。
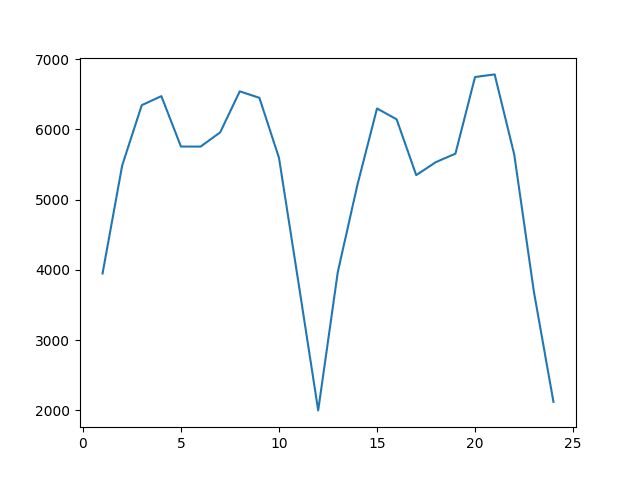
月度汽车销售数据集的持续观测值与RMSE的关系
我们可以使用t-12模型进行预测,并将其与测试数据进行绘制。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
from pandas import read_csv from sklearn.metrics import mean_squared_error from math import sqrt from matplotlib import pyplot # 加载数据 series = read_csv('car-sales.csv', header=0, index_col=0) # 准备数据 X = series.values train, test = X[0:-24], X[-24:] # 步进验证 history = [x for x in train] predictions = list() for i in range(len(test)): # 进行预测 yhat = history[-12] predictions.append(yhat) # 观测 history.append(test[i]) # 绘制预测值与观测值 pyplot.plot(test) pyplot.plot(predictions) pyplot.show() |
运行示例将绘制测试数据集(蓝色)与预测值(橙色)的图。
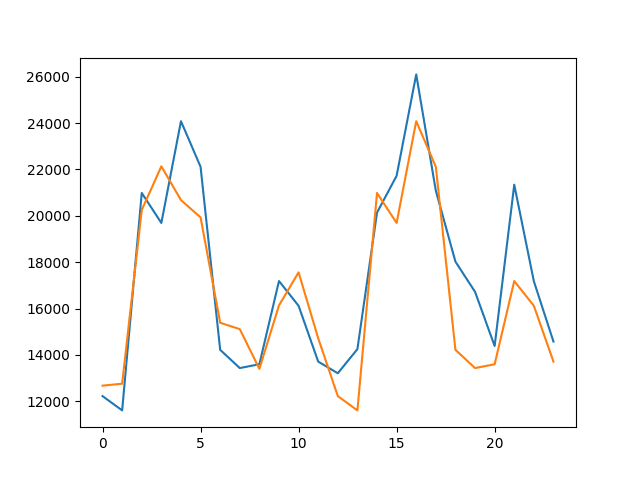
t-12持续模型预测值与测试数据集的折线图
您可以在文章中了解更多关于时间序列预测的持续性模型
扩展窗口预测
扩展窗口是指一个模型,它在所有可用的历史数据上计算一个统计量,并用它来做出预测。
随着越来越多的观测值被收集,它会不断增长,因此被称为扩展窗口。
两个好的起点统计量是历史观测值的均值和中位数。
下面的示例使用扩展窗口均值作为预测。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
from pandas import read_csv from sklearn.metrics import mean_squared_error from math import sqrt from numpy import mean # 加载数据 series = read_csv('car-sales.csv', header=0, index_col=0) # 准备数据 X = series.values train, test = X[0:-24], X[-24:] # 步进验证 history = [x for x in train] predictions = list() for i in range(len(test)): # 进行预测 yhat = mean(history) predictions.append(yhat) # 观测 history.append(test[i]) # 报告表现 rmse = sqrt(mean_squared_error(test, predictions)) print('RMSE: %.3f' % rmse) |
运行示例将打印该方法的RMSE评估。
|
1 |
RMSE: 5113.067 |
我们也可以用历史观测值的中位数重复同样的实验。完整的示例列在下面。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
from pandas import read_csv from sklearn.metrics import mean_squared_error from math import sqrt 从 numpy 导入 median # 加载数据 series = read_csv('car-sales.csv', header=0, index_col=0) # 准备数据 X = series.values train, test = X[0:-24], X[-24:] # 步进验证 history = [x for x in train] predictions = list() for i in range(len(test)): # 进行预测 yhat = median(history) predictions.append(yhat) # 观测 history.append(test[i]) # 报告表现 rmse = sqrt(mean_squared_error(test, predictions)) print('RMSE: %.3f' % rmse) |
再次运行示例将打印模型的技能。
我们可以看到,在这个问题上,历史均值比中位数产生了更好的结果,但两者都比使用优化持续值效果更差。
|
1 |
RMSE: 5527.408 |
我们可以绘制均值扩展窗口预测与测试数据集,以了解预测的实际情况。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
from pandas import read_csv from sklearn.metrics import mean_squared_error from matplotlib import pyplot from numpy import mean # 加载数据 series = read_csv('car-sales.csv', header=0, index_col=0) # 准备数据 X = series.values train, test = X[0:-24], X[-24:] # 步进验证 history = [x for x in train] predictions = list() for i in range(len(test)): # 进行预测 yhat = mean(history) predictions.append(yhat) # 观测 history.append(test[i]) # 绘制预测值与观测值 pyplot.plot(test) pyplot.plot(predictions) pyplot.show() |
图显示了糟糕的预测是什么样的,以及它如何完全不遵循数据的移动,除了略微上升的趋势。
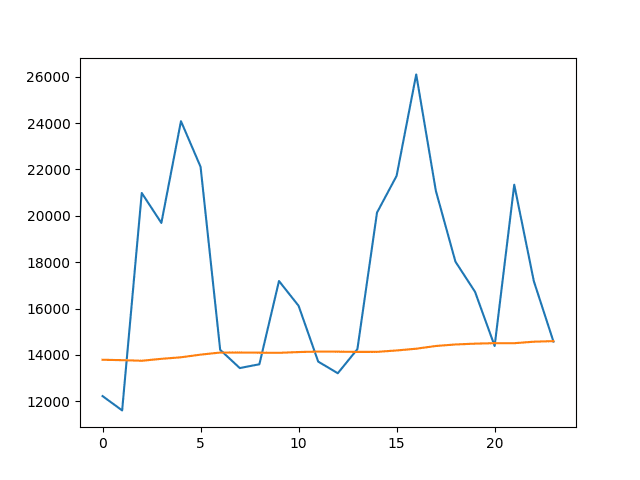
均值扩展窗口模型预测值与测试数据集的折线图
您可以在文章中找到更多关于扩展窗口统计的示例
滚动窗口预测
滚动窗口模型涉及计算一个固定连续的先前观测块的统计量,并将其用作预测。
它与扩展窗口非常相似,但窗口大小保持固定,并从最近的观测值开始倒数。
它可能在时间序列问题上更有用,在这些问题上,最近的滞后值比旧的滞后值更具预测性。
我们将自动检查从1个月到24个月(2年)的不同滚动窗口大小,并首先计算平均观测值并将其用作预测。完整的示例列在下面。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
from pandas import read_csv from sklearn.metrics import mean_squared_error from math import sqrt from matplotlib import pyplot from numpy import mean # 加载数据 series = read_csv('car-sales.csv', header=0, index_col=0) # 准备数据 X = series.values train, test = X[0:-24], X[-24:] window_sizes = range(1, 25) scores = list() for w in window_sizes: # 前向验证 history = [x for x in train] predictions = list() for i in range(len(test)): # 进行预测 yhat = mean(history[-w:]) predictions.append(yhat) # 观测 history.append(test[i]) # 报告性能 rmse = sqrt(mean_squared_error(test, predictions)) scores.append(rmse) print('w=%d RMSE:%.3f' % (w, rmse)) # 将得分绘制在窗口大小值上 pyplot.plot(window_sizes, scores) pyplot.show() |
运行示例将打印每个配置的滚动窗口大小和RMSE。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
w=1 RMSE:3947.200 w=2 RMSE:4350.413 w=3 RMSE:4701.446 w=4 RMSE:4810.510 w=5 RMSE:4649.667 w=6 RMSE:4549.172 w=7 RMSE:4515.684 w=8 RMSE:4614.551 w=9 RMSE:4653.493 w=10 RMSE:4563.802 w=11 RMSE:4321.599 w=12 RMSE:4023.968 w=13 RMSE:3901.634 w=14 RMSE:3907.671 w=15 RMSE:4017.276 w=16 RMSE:4084.080 w=17 RMSE:4076.399 w=18 RMSE:4085.376 w=19 RMSE:4101.505 w=20 RMSE:4195.617 w=21 RMSE:4269.784 w=22 RMSE:4258.226 w=23 RMSE:4158.029 w=24 RMSE:4021.885 |
还创建了窗口大小与误差的折线图。
结果表明,w=13的滚动窗口最好,RMSE为3,901辆月度汽车销量。
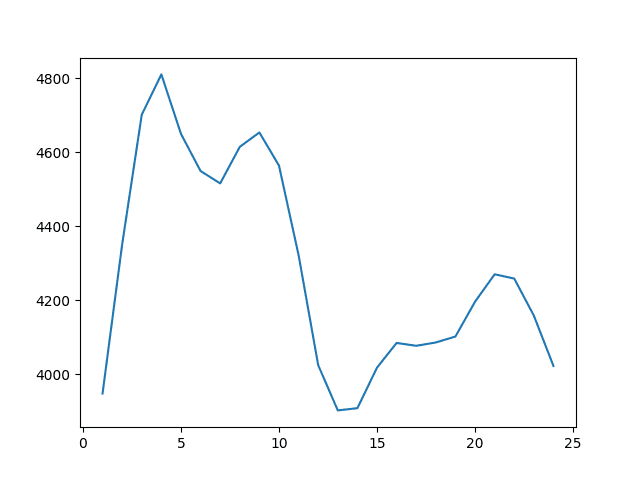
月度汽车销售数据集上均值预测的滚动窗口大小与RMSE的折线图
我们可以用中位数统计量重复这个实验。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
from pandas import read_csv from sklearn.metrics import mean_squared_error from math import sqrt from matplotlib import pyplot 从 numpy 导入 median # 加载数据 series = read_csv('car-sales.csv', header=0, index_col=0) # 准备数据 X = series.values train, test = X[0:-24], X[-24:] window_sizes = range(1, 25) scores = list() for w in window_sizes: # 前向验证 history = [x for x in train] predictions = list() for i in range(len(test)): # 进行预测 yhat = median(history[-w:]) predictions.append(yhat) # 观测 history.append(test[i]) # 报告性能 rmse = sqrt(mean_squared_error(test, predictions)) scores.append(rmse) print('w=%d RMSE:%.3f' % (w, rmse)) # 将得分绘制在窗口大小值上 pyplot.plot(window_sizes, scores) pyplot.show() |
再次运行示例将打印每个配置的窗口大小和RMSE。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
w=1 RMSE:3947.200 w=2 RMSE:4350.413 w=3 RMSE:4818.406 w=4 RMSE:4993.473 w=5 RMSE:5212.887 w=6 RMSE:5002.830 w=7 RMSE:4958.621 w=8 RMSE:4817.664 w=9 RMSE:4932.317 w=10 RMSE:4928.661 w=11 RMSE:4885.574 w=12 RMSE:4414.139 w=13 RMSE:4204.665 w=14 RMSE:4172.579 w=15 RMSE:4382.037 w=16 RMSE:4522.304 w=17 RMSE:4494.803 w=18 RMSE:4360.445 w=19 RMSE:4232.285 w=20 RMSE:4346.389 w=21 RMSE:4465.536 w=22 RMSE:4514.596 w=23 RMSE:4428.739 w=24 RMSE:4236.126 |
还创建了窗口大小与RMSE的折线图。
在这里,我们可以看到最佳结果是用窗口大小w=1获得的,RMSE为3947.200辆月度汽车销量,这基本上是一个t-1持续模型。
结果通常比优化持续性差,但比扩展窗口模型好。我们可以想象使用窗口观测值的加权组合会获得更好的结果,这个想法促使我们使用线性模型,如AR和ARIMA。
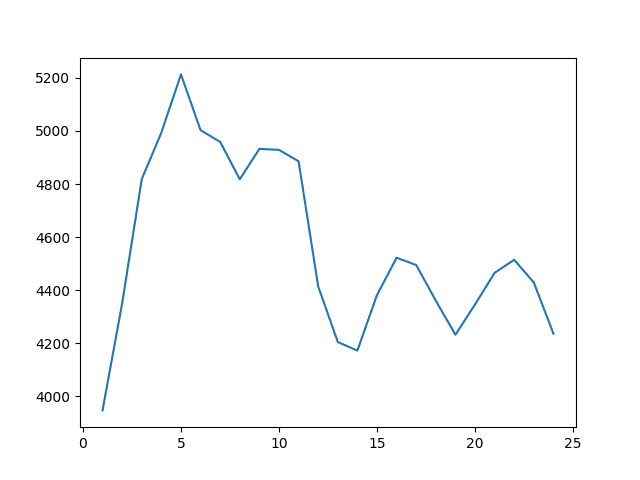
月度汽车销售数据集均值预测的滚动窗口大小与RMSE的折线图
同样,我们可以将来自更好模型(w=13的均值滚动窗口)的预测与实际观测值进行绘制,以了解预测的实际情况。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
from pandas import read_csv from sklearn.metrics import mean_squared_error from matplotlib import pyplot from numpy import mean # 加载数据 series = read_csv('car-sales.csv', header=0, index_col=0) # 准备数据 X = series.values train, test = X[0:-24], X[-24:] # 步进验证 history = [x for x in train] predictions = list() for i in range(len(test)): # 进行预测 yhat = mean(history[-13:]) predictions.append(yhat) # 观测 history.append(test[i]) # 绘制预测值与观测值 pyplot.plot(test) pyplot.plot(predictions) pyplot.show() |
运行代码将创建观测值(蓝色)与预测值(橙色)的折线图。
我们可以看到,模型更好地遵循了数据的水平,但同样没有遵循实际的上下波动。
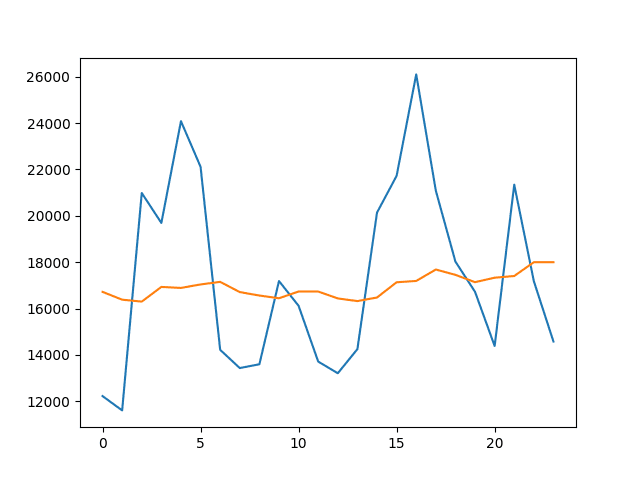
均值w=13滚动窗口模型预测值与测试数据集的折线图
您可以在文章中找到更多关于滚动窗口统计的示例
总结
在本教程中,您了解了在时间序列预测问题上计算最低可接受性能的重要性,以及确保您不会用更复杂的模型欺骗自己的方法。
具体来说,你学到了:
- 如何自动测试一系列持续性配置。
- 如何评估扩展窗口模型。
- 如何自动测试一系列滚动窗口配置。
您对基准预测模型或本文有任何疑问吗?
在评论中提出您的问题,我将尽力回答。





零评论?如此信息丰富、写得好且必不可少的帖子?这真是太糟糕了。
谢谢。
如何正确选择测试集大小?我发现的是,通常选择20%的数据,作为一个通用公式。
没有最好的方法。测试集必须具有代表性。
也许可以尝试不同的尺寸并比较结果。
也许可以与您的数据的领域专家交流。
为我的论文研究使用了这些方法。感谢这篇精彩的文章。
干得好!
你好!这是一篇非常棒的文章!
不过,我对Python代码有些难以理解。在“优化持续性预测”下的第一个Python代码中,yhat是如何计算的?
它是p(持续性值)的过去值的平均值吗?
非常感谢。
不,它只是找到了用于持续性模型的最佳负偏移量(-1、-2、-3……)。
这些模型是否预测数据集以外的未来时间步?或者它们是在预测保留数据的时间窗口?
您可以以任何您喜欢的方式使用它们。
我们总是根据模型在未在训练中看到的数据的预测技能来评估模型。
我不明白为什么我们在预测时要将测试数据(test[i])添加到历史数据中。
那是为了与预测进行比较,以了解我们的表现有多好。
你好,
感谢您的深刻见解。我正在处理一个不平衡的数据集(目标在总月数中仅显示15%)。我需要解决这种不平衡问题。但是,我应该在交叉验证之前对训练集进行此操作,还是以某种方式将不平衡修复程序集成到滚动窗口代码中,以便在每个窗口内进行不平衡修复?我不知道在理论和实践上哪种方法最好,所以任何见解都将不胜感激!
嗨 JK…以下资源可能对您感兴趣
https://arxiv.org/abs/2107.10709
嗨 James,感谢您的回复——这是一篇非常有用的论文,我一定会将其纳入我的研究。但是,我的当前项目被构建为一个分类问题(抱歉之前没有提及!),尽管它是时间序列。正如本教程所述:https://machinelearning.org.cn/smote-oversampling-for-imbalanced-classification/ 我现在认为我必须在每个CV窗口内解决不平衡问题(就像在每个fold内解决不平衡问题一样),而不是在运行任何CV之前。这是否正确?如果是这样,我不确定如何有效地将不平衡修复技术集成到滚动窗口CV生成器中。在Python中是否很容易实现?不幸的是,我在网上找不到任何例子。
感谢您的时间🙂