模拟退火是一种随机全局搜索优化算法。
这意味着它将随机性作为搜索过程的一部分。这使得该算法适用于非线性目标函数,而其他局部搜索算法在这些函数上表现不佳。
与随机爬山局部搜索算法一样,它修改单个解决方案并搜索搜索空间的相对局部区域,直到找到局部最优解。与爬山算法不同,它可能会接受较差的解决方案作为当前工作解决方案。
接受较差解决方案的可能性在搜索开始时很高,并随着搜索的进行而降低,这使得算法有机会首先定位全局最优解的区域,逃离局部最优解,然后爬山到最优解本身。
在本教程中,您将学习用于函数优化的模拟退火优化算法。
完成本教程后,您将了解:
- 模拟退火是一种用于函数优化的随机全局搜索算法。
- 如何在 Python 中从头开始实现模拟退火算法。
- 如何使用模拟退火算法并检查算法结果。
让我们开始吧。

在 Python 中从零开始实现模拟退火
图片来自 Susanne Nilsson,保留部分权利。
教程概述
本教程分为三个部分;它们是:
- 模拟退火
- 实现模拟退火
- 模拟退火实例
模拟退火
模拟退火是一种随机全局搜索优化算法。
该算法的灵感来自于冶金学中的退火,即金属被迅速加热到高温,然后缓慢冷却,这会增加其强度并使其更易于加工。
退火过程首先在高温下激发材料中的原子,使原子能够大量移动,然后缓慢降低它们的激发程度,使原子能够落入一种新的、更稳定的构型。
当温度较高时,材料中的原子更自由地移动,并通过随机运动,倾向于稳定在更好的位置。缓慢冷却使材料达到有序的晶态。
— 第 128 页,《优化算法》,2019年。
模拟退火优化算法可以被认为是随机爬山算法的修改版本。
随机爬山算法维护一个候选解决方案,并在搜索空间中以随机但受约束的步长从候选解决方案迈进。如果新点优于当前点,则当前点被新点替换。这个过程持续固定的迭代次数。
模拟退火以相同的方式执行搜索。主要区别在于,有时会接受不如当前点(较差的点)的新点。
较差的点是概率性接受的,接受比当前解决方案更差的解决方案的可能性是搜索温度以及该解决方案比当前解决方案差多少的函数。
该算法在决定何时用 R (其新调整的子代) 替换 S (原始候选解) 时与爬山算法不同。具体来说:如果 R 优于 S,我们将像往常一样始终用 R 替换 S。但是如果 R 劣于 S,我们仍然可能以一定的概率用 R 替换 S。
— 第 23 页,《元启发式算法要点》,2011年。
搜索的初始温度作为超参数提供,并随着搜索的进行而降低。可以使用许多不同的方案(退火时间表)在搜索过程中将温度从初始值降低到非常低的值,尽管通常将温度计算为迭代次数的函数。
一个流行的温度计算示例是所谓的“快速模拟退火”,计算方法如下:
- 温度 = 初始温度 / (迭代次数 + 1)
我们将迭代次数加一,以防迭代次数从零开始,避免除以零错误。
接受较差的解决方案时,会使用温度以及较差解决方案和当前解决方案的目标函数评估之间的差异。利用这些信息计算出一个介于 0 和 1 之间的值,表示接受较差解决方案的可能性。然后使用一个随机数对该分布进行采样,如果该随机数小于该值,则表示接受较差的解决方案。
正是这种接受概率,即所谓的 Metropolis 准则,使算法能够在温度较高时逃离局部最小值。
— 第 128 页,《优化算法》,2019年。
这被称为 Metropolis 接受准则,对于最小化,其计算方法如下:
- 准则 = exp( -(目标(新) – 目标(当前)) / 温度)
其中 exp() 是 e(数学常数)的指定参数的幂,而 objective(new) 和 objective(current) 是新的(较差的)和当前候选解的目标函数评估。
其结果是,较差的解决方案在搜索初期更有可能被接受,而在搜索后期则不太可能被接受。目的是在搜索初期的高温将有助于搜索定位全局最优的盆地,而搜索后期的低温将有助于算法精确定位全局最优。
温度开始时很高,允许过程在搜索空间中自由移动,希望在此阶段过程能找到一个具有最佳局部最小值的良好区域。然后温度缓慢降低,减少随机性并迫使搜索收敛到最小值。
— 第 128 页,《优化算法》,2019年。
现在我们熟悉了模拟退火算法,接下来看看如何从头实现它。
想要开始学习优化算法吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
实现模拟退火
在本节中,我们将探讨如何从头开始实现模拟退火优化算法。
首先,我们必须定义我们的目标函数以及目标函数的每个输入变量的边界。目标函数只是一个 Python 函数,我们将其命名为 objective()。边界将是一个二维数组,每个输入变量都有一个维度,用于定义变量的最小值和最大值。
例如,一维目标函数和边界定义如下:
|
1 2 3 4 5 6 |
# 目标函数 def objective(x): return 0 # 定义输入范围 bounds = asarray([[-5.0, 5.0]]) |
接下来,我们可以将初始点生成为问题边界内的随机点,然后使用目标函数对其进行评估。
|
1 2 3 4 5 |
... # 生成初始点 best = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] - bounds[:, 0]) # 评估初始点 best_eval = objective(best) |
我们需要维护“当前”解决方案,它是搜索的焦点,并可能被更好的解决方案替换。
|
1 2 3 |
... # 当前工作解决方案 curr, curr_eval = best, best_eval |
现在我们可以循环执行预定义次数的算法迭代,例如 100 或 1,000 次,定义为“n_iterations”。
|
1 2 3 4 |
... # 运行算法 for i in range(n_iterations): ... |
算法迭代的第一步是从当前工作解决方案生成一个新的候选解决方案,例如迈出一步。
这需要一个预定义的“step_size”参数,它与搜索空间的边界有关。我们将以高斯分布进行随机步进,其中均值是我们的当前点,标准差由“step_size”定义。这意味着大约 99% 的步进将在当前点的 3 * step_size 范围内。
|
1 2 3 |
... # 迈出一步 candidate = solution + randn(len(bounds)) * step_size |
我们不必以这种方式进行步进。您可能希望使用介于 0 和步长之间的均匀分布。例如
|
1 2 3 |
... # 迈出一步 candidate = solution + rand(len(bounds)) * step_size |
接下来,我们需要对其进行评估。
|
1 2 3 |
... # 评估候选点 candidate_eval = objective(candidate) |
然后我们需要检查这个新点的评估是否与当前最佳点一样好或更好,如果是,则用这个新点替换我们当前的最佳点。
这与作为搜索焦点的当前工作解决方案是分开的。
|
1 2 3 4 5 6 7 |
... # 检查新的最佳解决方案 if candidate_eval < best_eval: # 存储新的最佳点 best, best_eval = candidate, candidate_eval # 报告进度 print('>%d f(%s) = %.5f' % (i, best, best_eval)) |
接下来,我们需要准备替换当前的工作解决方案。
第一步是计算当前解决方案和当前工作解决方案的目标函数评估之间的差异。
|
1 2 3 |
... # 候选点和当前点评估之间的差异 diff = candidate_eval - curr_eval |
接下来,我们需要使用快速退火计划计算当前温度,其中“temp”是作为参数提供的初始温度。
|
1 2 3 |
... # 计算当前周期的温度 t = temp / float(i + 1) |
然后,我们可以计算接受性能低于当前工作解决方案的解决方案的可能性。
|
1 2 3 |
... # 计算 Metropolis 接受准则 metropolis = exp(-diff / t) |
最后,如果新点具有更好的目标函数评估(差异为负)或者目标函数更差但我们概率性地决定接受它,我们可以接受新点作为当前工作解决方案。
|
1 2 3 4 5 |
... # 检查是否应该保留新点 if diff < 0 or rand() < metropolis: # 存储新的当前点 curr, curr_eval = candidate, candidate_eval |
就是这样。
我们可以将这个模拟退火算法实现为一个可重用的函数,该函数接受目标函数名称、每个输入变量的边界、总迭代次数、步长和初始温度作为参数,并返回找到的最佳解决方案及其评估结果。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
# 模拟退火算法 def simulated_annealing(objective, bounds, n_iterations, step_size, temp): # 生成初始点 best = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] - bounds[:, 0]) # 评估初始点 best_eval = objective(best) # 当前工作解决方案 curr, curr_eval = best, best_eval # 运行算法 for i in range(n_iterations): # 迈出一步 candidate = curr + randn(len(bounds)) * step_size # 评估候选点 candidate_eval = objective(candidate) # 检查新的最佳解决方案 if candidate_eval < best_eval: # 存储新的最佳点 best, best_eval = candidate, candidate_eval # 报告进度 print('>%d f(%s) = %.5f' % (i, best, best_eval)) # 候选点和当前点评估之间的差异 diff = candidate_eval - curr_eval # 计算当前周期的温度 t = temp / float(i + 1) # 计算 Metropolis 接受准则 metropolis = exp(-diff / t) # 检查是否应该保留新点 if diff < 0 or rand() < metropolis: # 存储新的当前点 curr, curr_eval = candidate, candidate_eval return [best, best_eval] |
现在我们知道了如何在 Python 中实现模拟退火算法,接下来看看如何使用它来优化目标函数。
模拟退火实例
在本节中,我们将模拟退火优化算法应用于目标函数。
首先,我们来定义我们的目标函数。
我们将使用一个简单的一维 x^2 目标函数,其边界为 [-5, 5]。
下面的示例定义了该函数,然后为输入值的网格创建了函数响应面的线图,并用红线标记了 f(0.0) = 0.0 处的最佳值。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
# 凸单峰优化函数 from numpy import arange from matplotlib import pyplot # 目标函数 def objective(x): return x[0]**2.0 # 定义输入范围 r_min, r_max = -5.0, 5.0 # 以 0.1 为增量均匀采样输入范围 inputs = arange(r_min, r_max, 0.1) # 计算目标值 results = [objective([x]) for x in inputs] # 绘制输入与结果的线图 pyplot.plot(inputs, results) # 定义最优输入值 x_optima = 0.0 # 在最优输入处画一条竖线 pyplot.axvline(x=x_optima, ls='--', color='red') # 显示绘图 pyplot.show() |
运行示例会创建一个目标函数的线图,并清晰地标记出函数最优值。
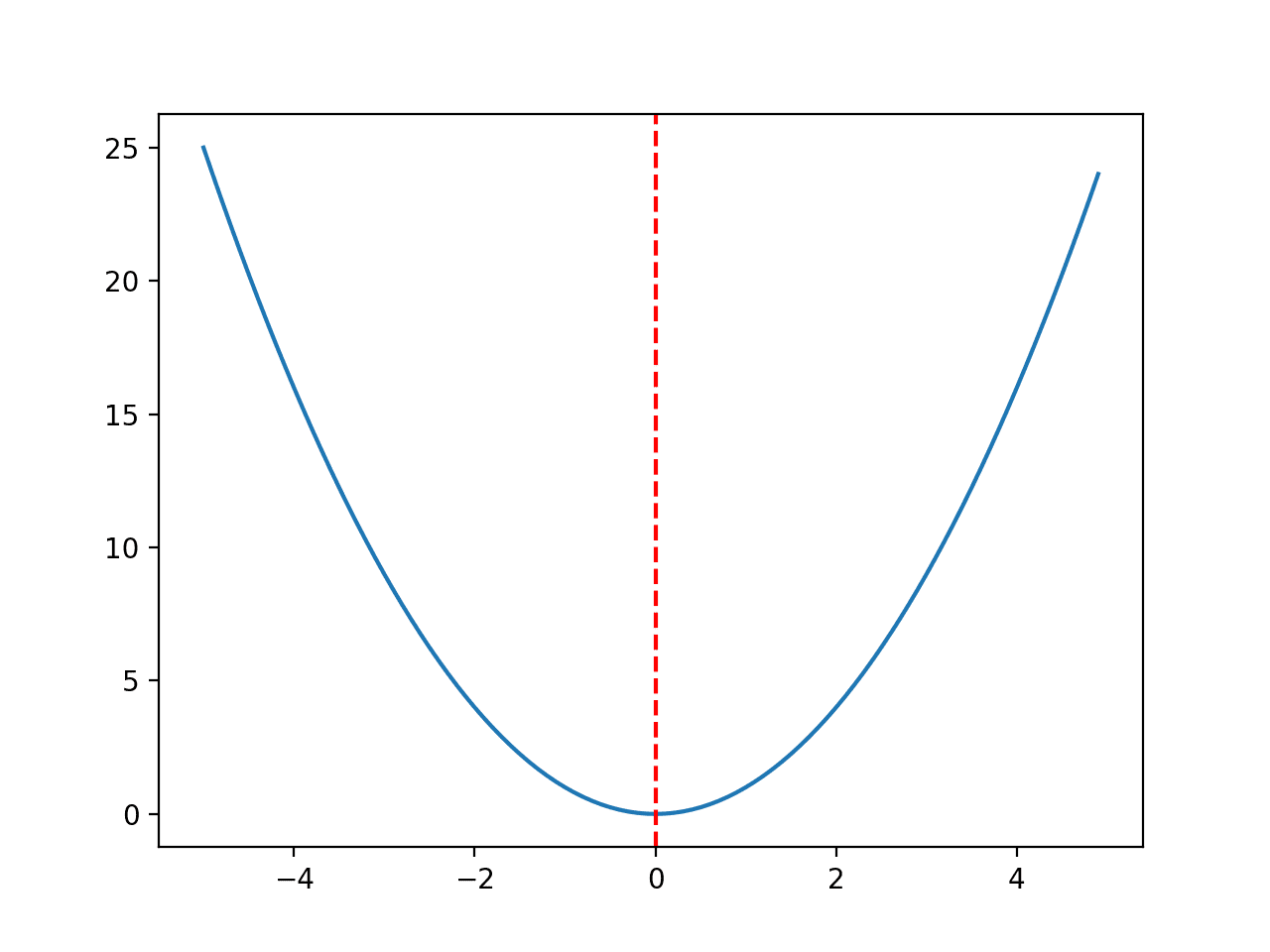
目标函数线图,最优值以红色虚线标记
在我们将优化算法应用于问题之前,我们先花点时间更好地理解接受准则。
首先,快速退火计划是迭代次数的指数函数。我们可以通过创建每个算法迭代温度的图来明确这一点。
我们将使用初始温度 10 和 100 次算法迭代,两者都是随意选择的。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
# 探索模拟退火的温度与算法迭代关系 from matplotlib import pyplot # 算法总迭代次数 iterations = 100 # 初始温度 initial_temp = 10 # 迭代次数数组,从 0 到 iterations - 1 iterations = [i for i in range(iterations)] # 每次迭代的温度 temperatures = [initial_temp/float(i + 1) for i in iterations] # 绘制迭代次数与温度的关系图 pyplot.plot(iterations, temperatures) pyplot.xlabel('Iteration') pyplot.ylabel('Temperature') pyplot.show() |
运行示例会计算每个算法迭代的温度,并创建算法迭代(x 轴)与温度(y 轴)的图。
我们可以看到温度呈指数级快速下降,以至于在 20 次迭代后低于 1,并在搜索的剩余部分保持低位。
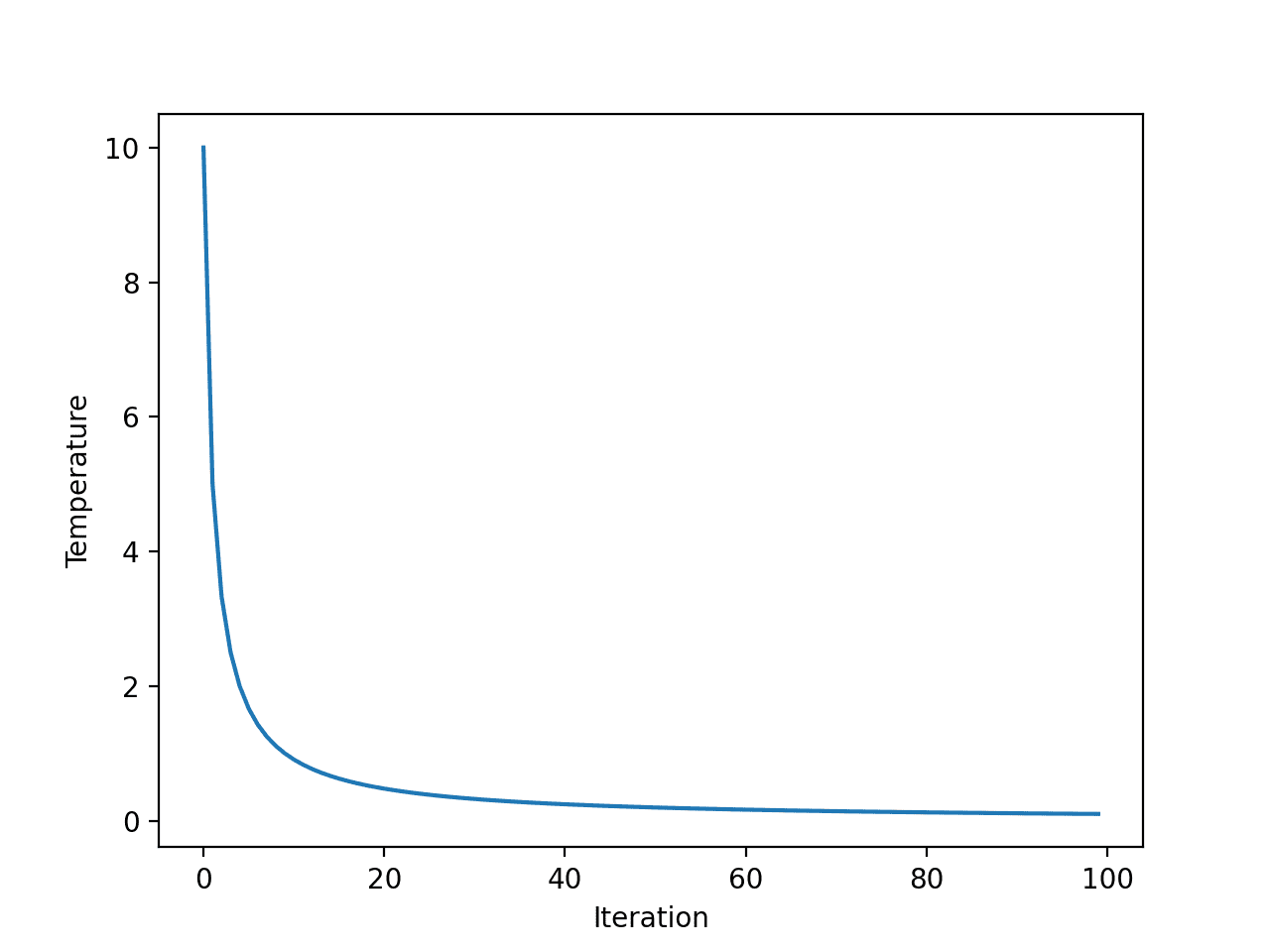
快速退火温度与算法迭代的线图
接下来,我们可以更好地了解 Metropolis 接受准则如何随温度变化而变化。
回想一下,该准则不仅是温度的函数,也是新点目标评估与当前工作解决方案的差异程度的函数。因此,我们将绘制几种不同“目标函数值差异”的准则,以查看其对接受概率的影响。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
# 探索模拟退火的 Metropolis 接受准则 from math import exp from matplotlib import pyplot # 算法总迭代次数 iterations = 100 # 初始温度 initial_temp = 10 # 迭代次数数组,从 0 到 iterations - 1 iterations = [i for i in range(iterations)] # 每次迭代的温度 temperatures = [initial_temp/float(i + 1) for i in iterations] # Metropolis 接受准则 differences = [0.01, 0.1, 1.0] for d in differences: metropolis = [exp(-d/t) for t in temperatures] # 绘制迭代次数与 Metropolis 准则的关系图 label = 'diff=%.2f' % d pyplot.plot(iterations, metropolis, label=label) # 初始化绘图 pyplot.xlabel('Iteration') pyplot.ylabel('Metropolis Criterion') pyplot.legend() pyplot.show() |
运行示例会计算每个算法迭代的 Metropolis 接受准则,使用每个迭代的温度(如前一节所示)。
该图有三条线,代表新较差解决方案与当前工作解决方案之间的三种差异。
我们可以看到,解决方案越差(差异越大),模型接受较差解决方案的可能性越小,无论算法迭代次数如何,这正如我们所料。我们还可以看到,在所有情况下,接受较差解决方案的可能性都随着算法迭代次数的增加而降低。
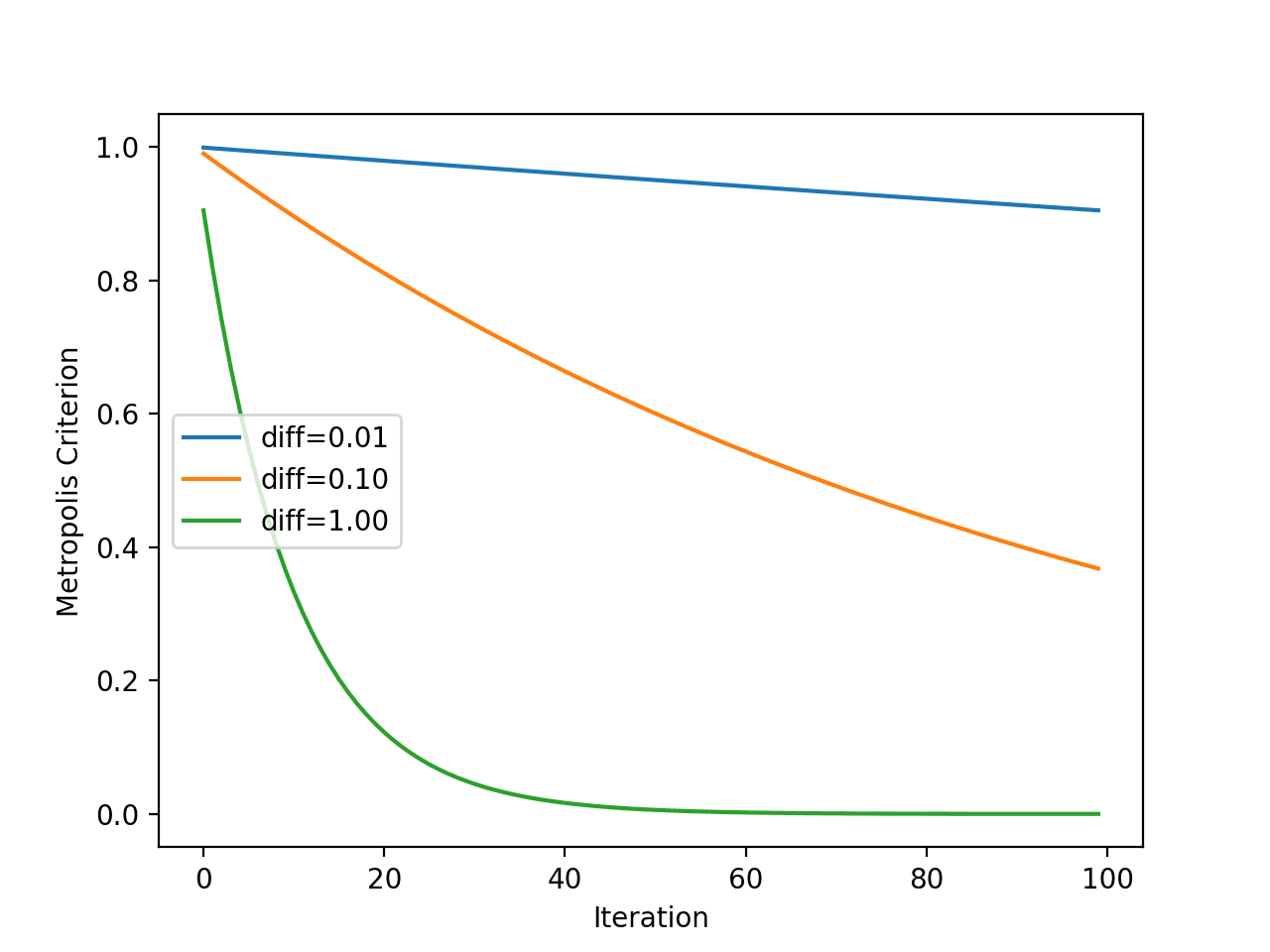
模拟退火 Metropolis 接受准则与算法迭代的线图
现在我们对温度和 Metropolis 接受准则随时间变化的特性更加熟悉了,接下来将模拟退火应用于我们的测试问题。
首先,我们将播种伪随机数生成器。
这通常不是必需的,但在本例中,我希望确保每次运行算法时都得到相同的结果(相同的随机数序列),以便我们以后可以绘制结果。
|
1 2 3 |
... # 播种伪随机数生成器 seed(1) |
接下来,我们可以定义搜索的配置。
在这种情况下,我们将进行 1,000 次算法迭代,并使用 0.1 的步长。鉴于我们使用高斯函数生成步长,这意味着大约 99% 的步长将落在给定点的 (0.1 * 3) 距离内,例如三个标准差。
我们还将使用 10.0 的初始温度。搜索过程对退火计划比对初始温度更敏感,因此,初始温度值几乎是任意的。
|
1 2 3 4 5 6 |
... n_iterations = 1000 # 定义最大步长 step_size = 0.1 # 初始温度 temp = 10 |
接下来,我们可以执行搜索并报告结果。
|
1 2 3 4 5 |
... # 执行模拟退火搜索 best, score = simulated_annealing(objective, bounds, n_iterations, step_size, temp) print('Done!') print('f(%s) = %f' % (best, score)) |
将所有这些结合起来,完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 |
# 一维目标函数的模拟退火搜索 from numpy import asarray from numpy import exp from numpy.random import randn from numpy.random import rand from numpy.random import seed # 目标函数 def objective(x): return x[0]**2.0 # 模拟退火算法 def simulated_annealing(objective, bounds, n_iterations, step_size, temp): # 生成初始点 best = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] - bounds[:, 0]) # 评估初始点 best_eval = objective(best) # 当前工作解决方案 curr, curr_eval = best, best_eval # 运行算法 for i in range(n_iterations): # 迈出一步 candidate = curr + randn(len(bounds)) * step_size # 评估候选点 candidate_eval = objective(candidate) # 检查新的最佳解决方案 if candidate_eval < best_eval: # 存储新的最佳点 best, best_eval = candidate, candidate_eval # 报告进度 print('>%d f(%s) = %.5f' % (i, best, best_eval)) # 候选点和当前点评估之间的差异 diff = candidate_eval - curr_eval # 计算当前周期的温度 t = temp / float(i + 1) # 计算 Metropolis 接受准则 metropolis = exp(-diff / t) # 检查是否应该保留新点 if diff < 0 or rand() < metropolis: # 存储新的当前点 curr, curr_eval = candidate, candidate_eval return [best, best_eval] # 播种伪随机数生成器 seed(1) # 定义输入范围 bounds = asarray([[-5.0, 5.0]]) # 定义总迭代次数 n_iterations = 1000 # 定义最大步长 step_size = 0.1 # 初始温度 temp = 10 # 执行模拟退火搜索 best, score = simulated_annealing(objective, bounds, n_iterations, step_size, temp) print('Done!') print('f(%s) = %f' % (best, score)) |
运行示例会报告搜索的进展,包括迭代次数、函数的输入以及每次检测到改进时目标函数的响应。
在搜索结束时,找到最佳解决方案并报告其评估结果。
注意:考虑到算法或评估过程的随机性,或者数值精度差异,您的结果可能会有所不同。请考虑多次运行示例并比较平均结果。
在这种情况下,我们可以在算法的 1,000 次迭代中看到大约 20 次改进,并且找到的解决方案非常接近最优输入 0.0,其评估结果为 f(0.0) = 0.0。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
>34 f([-0.78753544]) = 0.62021 >35 f([-0.76914239]) = 0.59158 >37 f([-0.68574854]) = 0.47025 >39 f([-0.64797564]) = 0.41987 >40 f([-0.58914623]) = 0.34709 >41 f([-0.55446029]) = 0.30743 >42 f([-0.41775702]) = 0.17452 >43 f([-0.35038542]) = 0.12277 >50 f([-0.15799045]) = 0.02496 >66 f([-0.11089772]) = 0.01230 >67 f([-0.09238208]) = 0.00853 >72 f([-0.09145261]) = 0.00836 >75 f([-0.05129162]) = 0.00263 >93 f([-0.02854417]) = 0.00081 >144 f([0.00864136]) = 0.00007 >149 f([0.00753953]) = 0.00006 >167 f([-0.00640394]) = 0.00004 >225 f([-0.00044965]) = 0.00000 >503 f([-0.00036261]) = 0.00000 >512 f([0.00013605]) = 0.00000 完成! f([0.00013605]) = 0.000000 |
查看搜索进度作为线图可能很有趣,该线图显示每次有改进时最佳解决方案评估的变化。
我们可以更新 simulated_annealing() 以跟踪每次有改进时的目标函数评估,并返回此分数列表。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
# 模拟退火算法 def simulated_annealing(objective, bounds, n_iterations, step_size, temp): # 生成初始点 best = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] - bounds[:, 0]) # 评估初始点 best_eval = objective(best) # 当前工作解决方案 curr, curr_eval = best, best_eval # 运行算法 for i in range(n_iterations): # 迈出一步 candidate = curr + randn(len(bounds)) * step_size # 评估候选点 candidate_eval = objective(candidate) # 检查新的最佳解决方案 if candidate_eval < best_eval: # 存储新的最佳点 best, best_eval = candidate, candidate_eval # 记录分数 scores.append(best_eval) # 报告进度 print('>%d f(%s) = %.5f' % (i, best, best_eval)) # 候选点和当前点评估之间的差异 diff = candidate_eval - curr_eval # 计算当前周期的温度 t = temp / float(i + 1) # 计算 Metropolis 接受准则 metropolis = exp(-diff / t) # 检查是否应该保留新点 if diff < 0 or rand() < metropolis: # 存储新的当前点 curr, curr_eval = candidate, candidate_eval return [best, best_eval, scores] |
然后我们可以创建这些分数的线图,以查看搜索过程中发现的每次改进的目标函数相对变化。
|
1 2 3 4 5 6 |
... # 最佳分数线图 pyplot.plot(scores, '.-') pyplot.xlabel('Improvement Number') pyplot.ylabel('Evaluation f(x)') pyplot.show() |
结合起来,下面列出了执行搜索和绘制搜索过程中改进解决方案的目标函数分数的完整示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 |
# 一维目标函数的模拟退火搜索 from numpy import asarray from numpy import exp from numpy.random import randn from numpy.random import rand from numpy.random import seed from matplotlib import pyplot # 目标函数 def objective(x): return x[0]**2.0 # 模拟退火算法 def simulated_annealing(objective, bounds, n_iterations, step_size, temp): # 生成初始点 best = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] - bounds[:, 0]) # 评估初始点 best_eval = objective(best) # 当前工作解决方案 curr, curr_eval = best, best_eval scores = list() # 运行算法 for i in range(n_iterations): # 迈出一步 candidate = curr + randn(len(bounds)) * step_size # 评估候选点 candidate_eval = objective(candidate) # 检查新的最佳解决方案 if candidate_eval < best_eval: # 存储新的最佳点 best, best_eval = candidate, candidate_eval # 记录分数 scores.append(best_eval) # 报告进度 print('>%d f(%s) = %.5f' % (i, best, best_eval)) # 候选点和当前点评估之间的差异 diff = candidate_eval - curr_eval # 计算当前周期的温度 t = temp / float(i + 1) # 计算 Metropolis 接受准则 metropolis = exp(-diff / t) # 检查是否应该保留新点 if diff < 0 or rand() < metropolis: # 存储新的当前点 curr, curr_eval = candidate, candidate_eval return [best, best_eval, scores] # 播种伪随机数生成器 seed(1) # 定义输入范围 bounds = asarray([[-5.0, 5.0]]) # 定义总迭代次数 n_iterations = 1000 # 定义最大步长 step_size = 0.1 # 初始温度 temp = 10 # 执行模拟退火搜索 best, score, scores = simulated_annealing(objective, bounds, n_iterations, step_size, temp) print('Done!') print('f(%s) = %f' % (best, score)) # 最佳分数线图 pyplot.plot(scores, '.-') pyplot.xlabel('Improvement Number') pyplot.ylabel('Evaluation f(x)') pyplot.show() |
运行示例会执行搜索并像以前一样报告结果。
创建了一个线图,显示了爬山搜索过程中每次改进的目标函数评估。我们可以在搜索过程中看到目标函数评估大约 20 次变化,初期变化较大,而在搜索结束时,随着算法收敛到最优值,变化非常小甚至察觉不到。
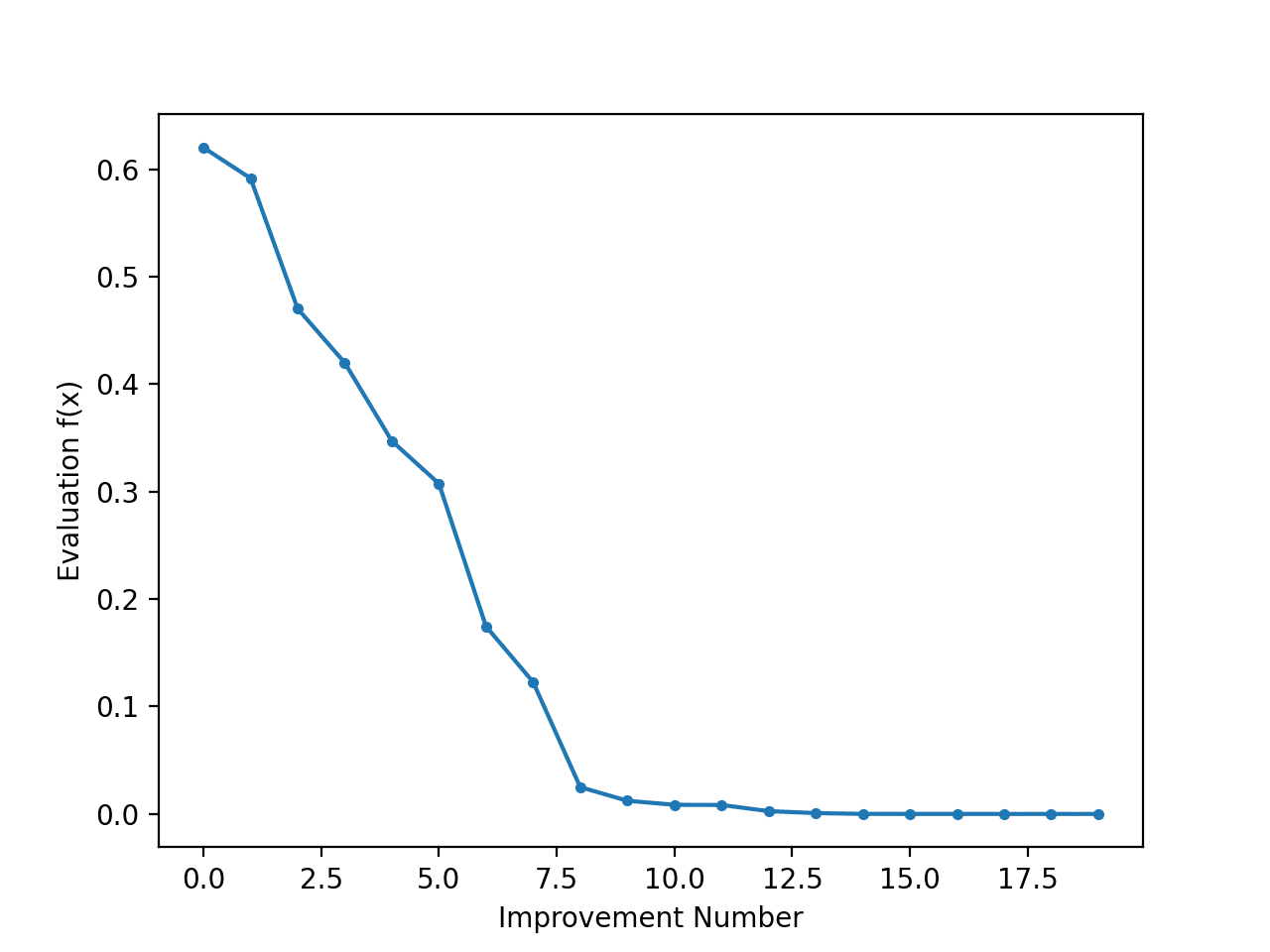
模拟退火搜索过程中每次改进的目标函数评估线图
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
论文
- 模拟退火优化, 1983.
书籍
文章
总结
在本教程中,您学习了用于函数优化的模拟退火优化算法。
具体来说,你学到了:
- 模拟退火是一种用于函数优化的随机全局搜索算法。
- 如何在 Python 中从头开始实现模拟退火算法。
- 如何使用模拟退火算法并检查算法结果。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。





嗨,Jason,
我通读了你的教程(顺便说一句,信息量很大,我正在学习……),除了最后一点,一切都 99.5% 正确。
也就是说,我的“最佳和得分”输出是一个单一数据点(f([1.96469186]) = 3.0000)。
我没有得到你在最后做的线图
结束?你是否必须将对象函数更改为与教程中不同的东西?我的“分数”图是空的?
不用回复了,我最终复制了你的脚本,它按预期工作了?我不确定我的哪里出错了,但它非常相似,除了代码的一些行写在不同的单元格中?
顺便说一句,很棒的教程,谢谢分享……
罗恩
干得好!
很抱歉听到这个消息,你是在命令行运行吗?
https://machinelearning.org.cn/faq/single-faq/how-do-i-run-a-script-from-the-command-line
不,Jason,我用的是 Jupyter notebook,而不是命令行?我的问题是一些缩进错误,以及我试验了一些你的初始值但从未将其恢复正常。吸取教训……希望如此 😉
这将帮助你复制代码而不会出现缩进错误
https://machinelearning.org.cn/faq/single-faq/how-do-i-copy-code-from-a-tutorial
Jason,我认为你的代码片段的缩进搞砸了。
谢谢,我将调查。
你推荐 Anaconda 用于机器学习程序,我真的很想亲自动手学习它。
我担心它可能无法在我的系统上运行:我的 2GB 内存笔记本电脑运行 32 位 Windows 7 操作系统(Service Pack 1)。
但是,应该有一个 Anaconda 包可以在我的笔记本电脑上运行,对吧?
顺便问一下,Anaconda 和 PyTorch 是一样的吗?
此外,你的哪本书有关于如何将 Windows 文本文件转换为 csv 格式的部分?
还有,你的书里有没有一个部分(连同 Python 源代码)可以帮助将数据文件存储到一个包含以下信息的数组中?(如下所示……)
20,20,21,1,1,7
7,7,1,1,21,20
21,21,20,1,7,20
7,7,7,7,7,1
弗朗西斯,
1.) 如果你认为 Anaconda 程序太大,你可以尝试 miniconda。它是 Anaconda 的一个较小的引导版本。
2.) Anaconda 和 PyTorch 不是一回事。
——Anaconda 是基于 python 构建的
——PyTorch 由 Facebook 人工智能研究实验室开发,使用 Python、C++ 和 CUDA 编写。
CUDA
3.) 如果你想了解更多关于数组的信息,我强烈建议你访问 Numpy.org
——他们有教程、示例以及各种操作数组的方法
希望这能帮助你完成你的任务。
罗恩
好建议,Ron!
也许可以尝试以另一种方式安装 Python?
这有助于您加载文件
https://machinelearning.org.cn/load-machine-learning-data-python/
这将帮助您保存结果
https://machinelearning.org.cn/how-to-save-a-numpy-array-to-file-for-machine-learning/
“此外,你的哪本书有关于如何将 Windows 文本文件转换为 csv 格式的部分?”
包含逗号分隔值的文本文件已经是 csv 格式文件(大致如此)。
您的示例数据可以通过多种方式存储在数组中——例如,查阅 numpy 中的 genfromtxt,从文本文件或 csv 文件创建数组,如您的第一个问题所示。
祝好!
数据几乎总是以 CSV 格式存在,或者可以轻松转换为 CSV 格式。
您可以通过以下方式在 Python 中加载 CSV 文件
https://machinelearning.org.cn/load-machine-learning-data-python/
嘿,Jason,喜欢你的作品,一个代码片段里有一个小小的拼写错误
candidte_eval = objective(candidate)谢谢!已修复。
嗨,Jason,
非常感谢您的信息,我一直在寻找这方面的信息,但没有找到很多……偶然你会有带约束的目标函数优化示例吗,例如车辆路径问题 (vrp)
谢谢 Jason
不客气。
好建议,谢谢!
如何用多个变量运行它,有人能帮我吗
你到底遇到了什么问题?
我需要用 7 个变量来实现这个,但我无法添加变量的数量,请帮我一下
为什么?具体问题是什么?
我应该输入一个包含两个或多个未知数的方程,并使用模拟退火来找到这些变量的值,使方程变为 0,所以你能帮我一下吗
我建议您首先定义一个函数,该函数接受未知数并使用输入值评估您的方程。
然后您可以配置一个优化算法,以根据您的目标函数搜索值。
如果这听起来仍然太具有挑战性,也许可以与您的老师讨论。
但是当我尝试添加一个额外变量,比如说 y 时,错误是索引 1 超出了大小为 1 的轴的边界,并且 best_eval = objective(best)
好吧,我想我这门课可能要挂了,但至少我试过了,谢谢你抽出时间回复,你的工作很棒
亲爱的,我将此代码用于我的问题,但它没有给我正确答案。
我尝试更改步长和 Temp 值,如果我增加步长,那么新的候选者将超出我的边界。但在尝试了温度和步长的反复试验值后,我没有得到最优值
也许这个算法不适合你的问题?
不,这不是理由。我使用了 scipy 库进行模拟退火方法,效果非常好。我还更改了目标函数“eggholder 方程”,它在您的实现中也无法正常工作,但在 scipy 中运行良好
也许上面的实现太简单了,需要根据你的新问题进行修改。
是的,也许吧,因为我也使用了你的 GA 方法,效果很好,但这个(你的实现)不行,而 scipy 的退火方法可以
Jason 先生,我想请问,如果我们要将此代码用于 C 语言,需要包含哪些内容?
你必须从头用 C 语言重写它。
Jason 先生,我需要实现这个算法来选择超参数 alpha、beta 和主题数的最佳值以及最佳连贯性,但我不知道如何操作。您能帮我一下吗?
当然,你具体有什么问题(也就是说,我没有能力为你修改代码)?
我需要用两个变量运行它,目标函数是连贯性值。谢谢您抽出时间回复
如果你的函数定义得很好,你可以尝试使用这里的相同算法。但是,如果你的函数不是凸的,模拟退火高度依赖于初始值。
谢谢 Jason,好文章!为我的多变量目标函数调整代码轻而易举。
这本电子书是否详细阐述了步长选择、新候选者的 Gaussian vs uniform 分布、收敛性等方面?换句话说,您在书中是否提供了调整算法以适应函数的实用信息?
书中没有关于蒙特卡洛的信息吗?
顺便说一下,在您的代码中,只有初始点受限于定义的边界,后续迭代的候选点不受范围限制。
感谢 Arnaud 的好评!以下提供了我们所有电子书的信息
https://machinelearning.org.cn/products/
我需要实现这个算法来为 LS-SVM 模型选择超参数(gamma, sigma)的最佳值
我需要一段代码!
嗨,boumeftah……为此,我建议您研究贝叶斯优化
https://towardsdatascience.com/a-conceptual-explanation-of-bayesian-model-based-hyperparameter-optimization-for-machine-learning-b8172278050f