数据转换能够帮助数据科学家将原始数据提炼、标准化和统一,使其成为适合分析的格式。这些转换不仅仅是程序步骤,它们在减轻偏差、处理偏斜分布和增强统计模型的鲁棒性方面至关重要。本章将主要关注如何处理偏斜数据。通过以 Ames 住房数据集中的“SalePrice”(销售价格)和“YearBuilt”(建造年份)属性为例,您将看到正偏斜和负偏斜数据的示例,以及如何使用转换来对其分布进行规范化。
让我们开始吧。

告别偏态:数据科学家的转换技巧
Suzanne D. Williams 拍摄。部分权利保留。
概述
本文分为五个部分,它们是:
- 理解偏度和转换的必要性
- 处理正偏斜的策略
- 处理负偏斜的策略
- 转换的统计评估
- 选择正确的转换
理解偏度和转换的必要性
偏度是衡量数据分布围绕其均值不对称程度的统计量。简单来说,它表明大部分数据是聚集在尺度的一侧,而另一侧则有一条长长的尾巴。在数据分析中,您会遇到两种类型的偏度:
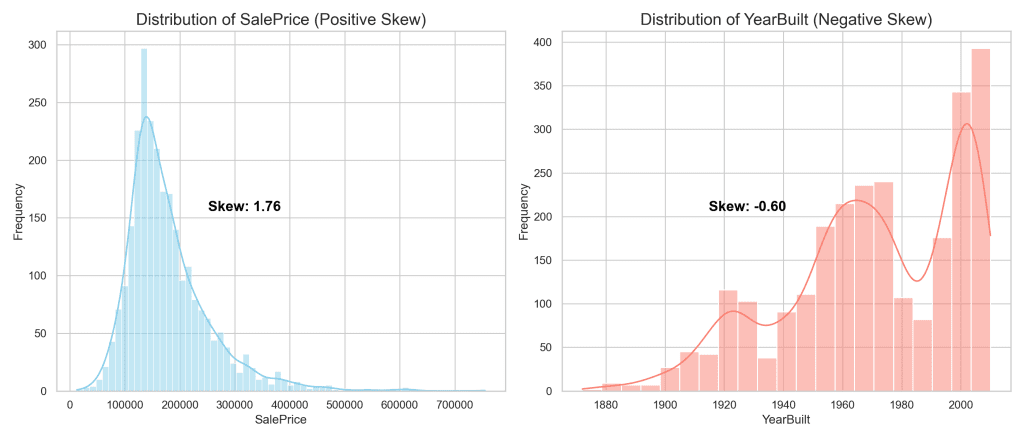
- 正偏斜:当分布的尾部延伸到峰值的右侧(较高值)时,就会发生这种情况。大多数数据点聚集在尺度的较低端,这意味着虽然大多数值相对较低,但有少数值异常高。“SalePrice”属性在 Ames 数据集中就是正偏斜的一个例子,因为大多数房屋的售价较低,但少数房屋的售价却显著较高。
- 负偏斜:相反,当分布的尾部向左侧(较低值)延伸时,就会发生负偏斜。在这种情况下,数据集中在尺度的较高端,而较低的值则形成少量尾巴。“YearBuilt”特征是负偏斜的一个完美例子,表明虽然大多数房屋建造于较近的年份,但一小部分可以追溯到更早的时期。
为了更好地理解这些概念,让我们可视化偏度。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 |
# 导入必要的库 import pandas as pd import matplotlib.pyplot as plt import seaborn as sns import numpy as np from scipy.stats import boxcox, yeojohnson from sklearn.preprocessing import QuantileTransformer # 加载数据集 Ames = pd.read_csv('Ames.csv') # 计算偏度 sale_price_skew = Ames['SalePrice'].skew() year_built_skew = Ames['YearBuilt'].skew() # 设置 seaborn 的样式 sns.set(style='whitegrid') # 创建一个包含 2 个子图的图形(1 行,2 列) fig, ax = plt.subplots(1, 2, figsize=(14, 6)) # 绘制 SalePrice(正偏斜) sns.histplot(Ames['SalePrice'], kde=True, ax=ax[0], color='skyblue') ax[0].set_title('SalePrice 分布(正偏斜)', fontsize=16) ax[0].set_xlabel('SalePrice') ax[0].set_ylabel('频率') # 注释偏度 ax[0].text(0.5, 0.5, f'偏度: {sale_price_skew:.2f}', transform=ax[0].transAxes, horizontalalignment='right', color='black', weight='bold', fontsize=14) # 绘制 YearBuilt(负偏斜) sns.histplot(Ames['YearBuilt'], kde=True, ax=ax[1], color='salmon') ax[1].set_title('YearBuilt 分布(负偏斜)', fontsize=16) ax[1].set_xlabel('YearBuilt') ax[1].set_ylabel('频率') # 注释偏度 ax[1].text(0.5, 0.5, f'偏度: {year_built_skew:.2f}', transform=ax[1].transAxes, horizontalalignment='right', color='black', weight='bold', fontsize=14) plt.tight_layout() plt.show() |
“SalePrice”图表显示出明显的右偏斜分布,凸显了偏度在数据分析中的挑战。这种分布会使预测建模复杂化,并掩盖洞察力,从而难以得出准确的结论。相比之下,“YearBuilt”则表现出负偏斜,其分布表明较新的房屋占主导地位,而较旧的房屋则形成了左侧的长尾。
通过数据转换来解决偏度不仅仅是统计调整;它是发掘精确、可操作见解的关键步骤。通过应用转换,您可以减轻偏度的影响,从而促进更可靠和更具解释性的分析。此规范化过程提高了您进行有意义的数据科学的能力,而不仅仅是满足统计先决条件。它强调了您提高数据清晰度和实用性的承诺,为后续数据转换探索中的深刻、有影响力的发现奠定了基础。
通过我的书 《数据科学入门指南》 来启动您的项目。它提供了带有工作代码的自学教程。
处理正偏斜的策略
为了克服正偏斜,您可以使用五种关键转换:对数转换、平方根转换、Box-Cox 转换、Yeo-Johnson 转换和分位数转换。每种方法都旨在减轻偏度,提高数据的可分析性。
对数转换
此方法特别适用于右偏斜数据,通过取所有数据点的自然对数来有效减小大规模差异。这种数据范围的压缩使其更容易进行进一步的统计分析。
|
1 2 3 |
# 应用对数转换 Ames['Log_SalePrice'] = np.log(Ames['SalePrice']) print(f"对数转换后的偏度: {Ames['Log_SalePrice'].skew():.5f}") |
您可以看到偏度已减小
|
1 |
对数转换后的偏度: 0.04172 |
平方根转换
作为比对数转换更温和的方法,非常适合中度偏斜的数据。通过将平方根应用于每个数据点,它会减小偏度并减弱异常值的影响,使分布更对称。
|
1 2 3 |
# 应用平方根转换 Ames['Sqrt_SalePrice'] = np.sqrt(Ames['SalePrice']) print(f"平方根转换后的偏度: {Ames['Sqrt_SalePrice'].skew():.5f}") |
输出如下:
|
1 |
平方根转换后的偏度: 0.90148 |
Box-Cox 转换
通过优化转换参数 lambda (λ) 来提供灵活性,仅适用于正数据。Box-Cox 方法系统地找到最佳幂转换以减小偏度并稳定方差,从而提高数据的正态性。
|
1 2 3 4 5 6 7 |
# 在检查所有值为正后应用 Box-Cox 转换 if (Ames['SalePrice'] > 0).all(): Ames['BoxCox_SalePrice'], _ = boxcox(Ames['SalePrice']) else: # 考虑替代转换或处理策略 print("并非所有 SalePrice 值都为正。请考虑使用 Yeo-Johnson 或处理负值。") print(f"Box-Cox 转换后的偏度: {Ames['BoxCox_SalePrice'].skew():.5f}") |
这是迄今为止最好的转换,因为偏度非常接近零
|
1 |
Box-Cox 转换后的偏度: -0.00436 |
Yeo-Johnson 转换
上述转换仅适用于正数据。Yeo-Johnson 与 Box-Cox 类似,但适用于正数和非正数数据。它通过最佳转换参数来修改数据。这种适应性使其能够处理更广泛数据值的偏度,从而提高其对统计模型的拟合度。
|
1 2 3 |
# 应用 Yeo-Johnson 转换 Ames['YeoJohnson_SalePrice'], _ = yeojohnson(Ames['SalePrice']) print(f"Yeo-Johnson 转换后的偏度: {Ames['YeoJohnson_SalePrice'].skew():.5f}") |
与 Box-Cox 类似,转换后的偏度非常接近零
|
1 |
Yeo-Johnson 转换后的偏度: -0.00437 |
分位数转换
分位数转换将数据映射到指定的分布,例如正态分布,通过将数据点均匀地分布在所选分布中来有效处理偏度。此转换规范了数据的形状,专注于使分布更均匀或呈高斯分布,而不会假设其非线性性质和将数据还原为其原始形式的难度会直接使线性模型受益。
|
1 2 3 4 |
# 应用分位数转换以遵循正态分布 quantile_transformer = QuantileTransformer(output_distribution='normal', random_state=0) Ames['Quantile_SalePrice'] = quantile_transformer.fit_transform(Ames['SalePrice'].values.reshape(-1, 1)).flatten() print(f"分位数转换后的偏度: {Ames['Quantile_SalePrice'].skew():.5f}") |
由于此转换通过暴力法将数据拟合到高斯分布,因此偏度最接近零
|
1 |
分位数转换后的偏度: 0.00286 |
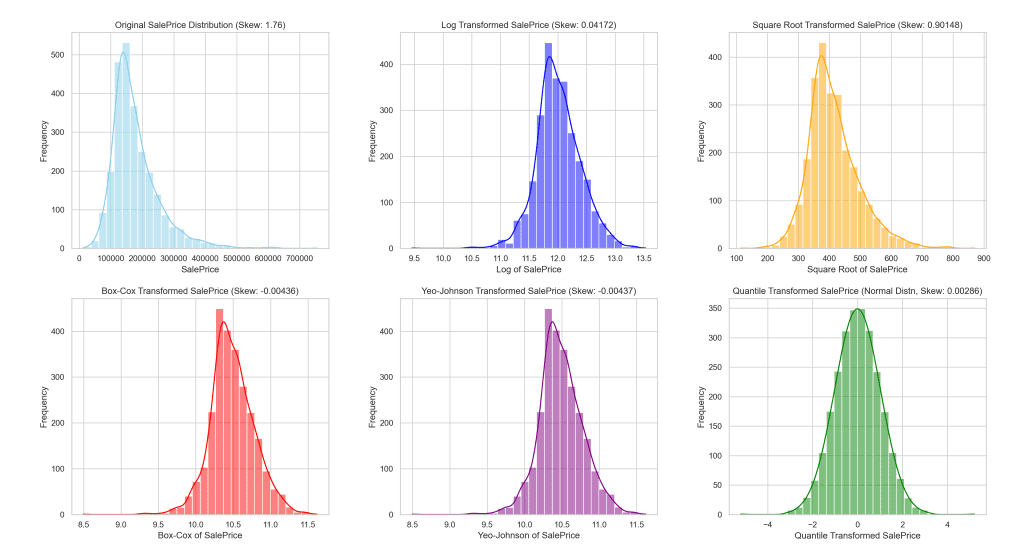
为了说明这些转换的效果,让我们看看应用每种方法之前和之后“SalePrice”分布的视觉表示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 |
# 绘制分布 fig, axes = plt.subplots(2, 3, figsize=(18, 15)) # 调整为额外的绘图 # 展平 axes 数组以便于索引 axes = axes.flatten() # 隐藏未使用的子图轴 for ax in axes[6:]: ax.axis('off') # 原始 SalePrice 分布 sns.histplot(Ames['SalePrice'], kde=True, bins=30, color='skyblue', ax=axes[0]) axes[0].set_title('原始 SalePrice 分布 (偏度: 1.76)') axes[0].set_xlabel('SalePrice') axes[0].set_ylabel('频率') # 对数转换的 SalePrice sns.histplot(Ames['Log_SalePrice'], kde=True, bins=30, color='blue', ax=axes[1]) axes[1].set_title('对数转换的 SalePrice (偏度: 0.04172)') axes[1].set_xlabel('SalePrice 的对数') axes[1].set_ylabel('频率') # 平方根转换的 SalePrice sns.histplot(Ames['Sqrt_SalePrice'], kde=True, bins=30, color='orange', ax=axes[2]) axes[2].set_title('平方根转换的 SalePrice (偏度: 0.90148)') axes[2].set_xlabel('SalePrice 的平方根') axes[2].set_ylabel('频率') # Box-Cox 转换的 SalePrice sns.histplot(Ames['BoxCox_SalePrice'], kde=True, bins=30, color='red', ax=axes[3]) axes[3].set_title('Box-Cox 转换的 SalePrice (偏度: -0.00436)') axes[3].set_xlabel('Box-Cox 的 SalePrice') axes[3].set_ylabel('频率') # Yeo-Johnson 转换的 SalePrice sns.histplot(Ames['YeoJohnson_SalePrice'], kde=True, bins=30, color='purple', ax=axes[4]) axes[4].set_title('Yeo-Johnson 转换的 SalePrice (偏度: -0.00437)') axes[4].set_xlabel('Yeo-Johnson 的 SalePrice') axes[4].set_ylabel('频率') # 分位数转换的 SalePrice (正态分布) sns.histplot(Ames['Quantile_SalePrice'], kde=True, bins=30, color='green', ax=axes[5]) axes[5].set_title('分位数转换的 SalePrice (正态分布, 偏度: 0.00286)') axes[5].set_xlabel('分位数转换的 SalePrice') axes[5].set_ylabel('频率') plt.tight_layout(pad=4.0) plt.show() |
以下可视化提供了并排比较,帮助您更好地理解每种转换对住房价格分布的影响。
此可视化为每种转换方法如何改变“SalePrice”的分布提供了一个清晰的参考,展示了其向更正态分布迈进的效果。
处理负偏斜的策略
为了克服负偏斜,您可以使用五种关键转换:平方、立方、Box-Cox、Yeo-Johnson 和分位数转换。每种方法都旨在减轻偏度,提高数据的可分析性。
平方转换
这涉及将数据集中的每个数据点进行平方(即将其提高到 2 次幂)。平方转换通过比高值更分散低值来有效地减小负偏斜。然而,当所有数据点都为正且负偏斜程度不极端时,它更有效。
|
1 2 3 |
# 应用平方转换 Ames['Squared_YearBuilt'] = Ames['YearBuilt'] ** 2 print(f"平方转换后的偏度: {Ames['Squared_YearBuilt'].skew():.5f}") |
输出结果为:
|
1 |
平方转换后的偏度: -0.57207 |
立方转换
与平方转换类似,但涉及将每个数据点提高到 3 次幂。立方转换可以进一步减小负偏斜,尤其是在平方转换不足的情况下。它在分散值方面更具侵略性,这可以使更具负偏斜的分布受益。
|
1 2 3 |
# 应用立方转换 Ames['Cubed_YearBuilt'] = Ames['YearBuilt'] ** 3 print(f"立方转换后的偏度: {Ames['Cubed_YearBuilt'].skew():.5f}") |
输出结果为:
|
1 |
立方转换后的偏度: -0.54539 |
Box-Cox 转换
一种更复杂的方法,它找到最佳的 lambda (λ) 参数将数据转换为正态形状。该转换仅对正数据定义。Box-Cox 转换通过使数据更对称,对包括负偏斜在内的各种分布非常有效。对于负偏斜数据,通常会找到一个正 lambda,应用一种有效减小偏度的转换。
|
1 2 3 4 5 6 7 |
# 在检查所有值为正后应用 Box-Cox 转换 if (Ames['YearBuilt'] > 0).all(): Ames['BoxCox_YearBuilt'], _ = boxcox(Ames['YearBuilt']) else: # 考虑替代转换或处理策略 print("并非所有的YearBuilt值都为正数。考虑使用Yeo-Johnson或处理负值。") print(f"Box-Cox变换后的偏度:{Ames['BoxCox_YearBuilt'].skew():.5f}") |
可以看出,偏度比之前更接近零。
|
1 |
Box-Cox变换后的偏度:-0.12435 |
Yeo-Johnson 转换
与Box-Cox变换类似,但Yeo-Johnson旨在同时处理正数和负数数据。对于负偏斜数据,即使存在负值,Yeo-Johnson变换也能使分布正常化。它以一种减少偏斜的方式调整数据,使其对于混合正值和负值的数据集特别通用。
|
1 2 3 |
# 应用 Yeo-Johnson 转换 Ames['YeoJohnson_YearBuilt'], _ = yeojohnson(Ames['YearBuilt']) print(f"Yeo-Johnson变换后的偏度:{Ames['YeoJohnson_YearBuilt'].skew():.5f}") |
与Box-Cox类似,您会看到偏度更接近零。
|
1 |
Yeo-Johnson变换后的偏度:-0.12435 |
分位数转换
此方法根据数据的分位数将其转换为遵循指定分布(例如正态分布)。它不假设输入数据具有任何特定的分布形状。当应用于负偏斜数据时,分位数变换可以有效地使分布正常化。它对于处理异常值和使数据分布统一或正态特别有用,而与原始偏斜无关。
|
1 2 3 4 |
# 应用分位数转换以遵循正态分布 quantile_transformer = QuantileTransformer(output_distribution='normal', random_state=0) Ames['Quantile_YearBuilt'] = quantile_transformer.fit_transform(Ames['YearBuilt'].values.reshape(-1, 1)).flatten() print(f"分位数变换后的偏度:{Ames['Quantile_YearBuilt'].skew():.5f}") |
正如您在正偏斜情况下看到的那样,分位数变换提供了最佳结果,因为其产生的偏度最接近零。
|
1 |
分位数变换后的偏度:0.02713 |
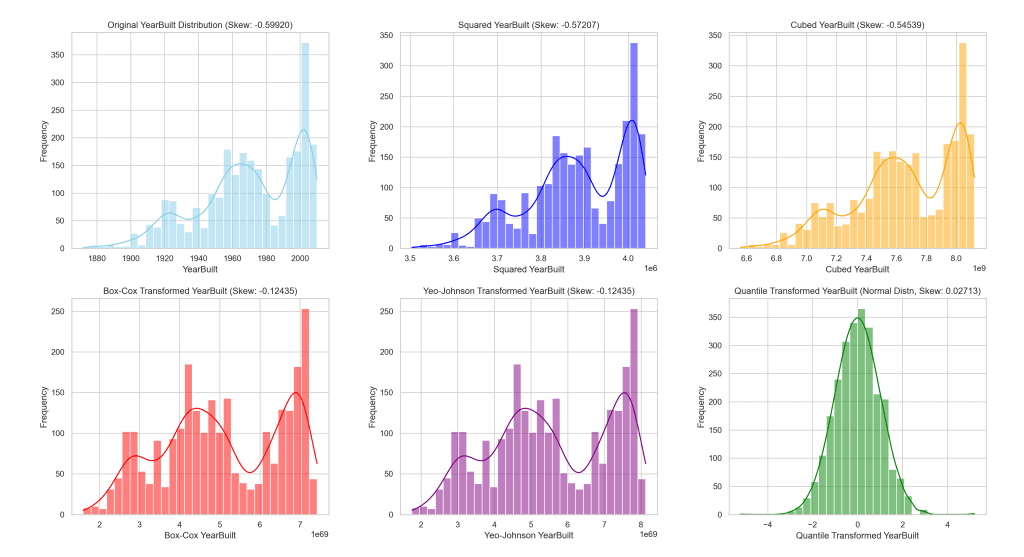
为了说明这些变换的效果,让我们来看一下在应用每种方法之前和之后“YearBuilt”分布的视觉表示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 |
# 绘制分布 fig, axes = plt.subplots(2, 3, figsize=(18, 15)) # 展平 axes 数组以便于索引 axes = axes.flatten() # 原始YearBuilt分布 sns.histplot(Ames['YearBuilt'], kde=True, bins=30, color='skyblue', ax=axes[0]) axes[0].set_title(f'原始YearBuilt分布 (偏度: {Ames["YearBuilt"].skew():.5f})') axes[0].set_xlabel('YearBuilt') axes[0].set_ylabel('频率') # 平方YearBuilt sns.histplot(Ames['Squared_YearBuilt'], kde=True, bins=30, color='blue', ax=axes[1]) axes[1].set_title(f'平方YearBuilt (偏度: {Ames["Squared_YearBuilt"].skew():.5f})') axes[1].set_xlabel('平方YearBuilt') axes[1].set_ylabel('频率') # 立方YearBuilt sns.histplot(Ames['Cubed_YearBuilt'], kde=True, bins=30, color='orange', ax=axes[2]) axes[2].set_title(f'立方YearBuilt (偏度: {Ames["Cubed_YearBuilt"].skew():.5f})') axes[2].set_xlabel('立方YearBuilt') axes[2].set_ylabel('频率') # Box-Cox变换的YearBuilt sns.histplot(Ames['BoxCox_YearBuilt'], kde=True, bins=30, color='red', ax=axes[3]) axes[3].set_title(f'Box-Cox变换的YearBuilt (偏度: {Ames["BoxCox_YearBuilt"].skew():.5f})') axes[3].set_xlabel('Box-Cox YearBuilt') axes[3].set_ylabel('频率') # Yeo-Johnson变换的YearBuilt sns.histplot(Ames['YeoJohnson_YearBuilt'], kde=True, bins=30, color='purple', ax=axes[4]) axes[4].set_title(f'Yeo-Johnson变换的YearBuilt (偏度: {Ames["YeoJohnson_YearBuilt"].skew():.5f})') axes[4].set_xlabel('Yeo-Johnson YearBuilt') axes[4].set_ylabel('频率') # 分位数变换的YearBuilt(正态分布) sns.histplot(Ames['Quantile_YearBuilt'], kde=True, bins=30, color='green', ax=axes[5]) axes[5].set_title(f'分位数变换的YearBuilt (正态分布, 偏度: {Ames["Quantile_YearBuilt"].skew():.5f})') axes[5].set_xlabel('分位数变换的YearBuilt') axes[5].set_ylabel('频率') plt.tight_layout(pad=4.0) plt.show() |
下面的可视化提供了并排比较,帮助我们更好地理解每种变换对该特征的影响。
此可视化清楚地展示了每种变换方法如何改变“YearBuilt”的分布,并说明了实现更正态分布的效果。
想开始学习数据科学新手指南吗?
立即参加我的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
转换的统计评估
您如何知道变换后的数据匹配正态分布?
Kolmogorov-Smirnov(KS)检验是一种**非参数检验**,用于确定样本是否来自具有特定分布的总体。与假设数据具有特定分布形式(通常是正态分布)的参数检验不同,非参数检验不作任何此类假设。这一特性使其在数据变换的背景下非常有用,因为它有助于评估变换后的数据集与正态分布的接近程度。KS检验将样本数据的累积分布函数(CDF)与已知分布(在此例中为正态分布)的CDF进行比较,并提供一个检验统计量来量化两者之间的距离。
零假设和备择假设
- 零假设($H_0$): 数据遵循指定的分布(在此例中为正态分布)。
- 备择假设($H_1$): 数据不遵循指定的分布。
在此上下文中,KS检验用于评估变换后数据的经验分布与正态分布之间的拟合优度。检验统计量衡量样本的经验分布函数与参考分布的累积分布函数之间的最大差异。较小的检验统计量表明分布相似。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# 从scipy.stats导入Kolmogorov-Smirnov检验 from scipy.stats import kstest # 对10种情况运行KS检验 transformations = ["Log_SalePrice", "Sqrt_SalePrice", "BoxCox_SalePrice", "YeoJohnson_SalePrice", "Quantile_SalePrice", "Squared_YearBuilt", "Cubed_YearBuilt", "BoxCox_YearBuilt", "YeoJohnson_YearBuilt", "Quantile_YearBuilt"] # 在执行KS检验之前对变换进行标准化 ks_test_results = {} for transformation in transformations: standardized_data = (Ames[transformation] - Ames[transformation].mean()) / Ames[transformation].std() ks_stat, ks_p_value = kstest(standardized_data, 'norm') ks_test_results[transformation] = (ks_stat, ks_p_value) # 将结果转换为DataFrame以便于比较 ks_test_results_df = pd.DataFrame.from_dict(ks_test_results, orient='index', columns=['KS Statistic', 'P-Value']) print(ks_test_results_df.round(5)) |
上面的代码将打印如下表格:
|
1 2 3 4 5 6 7 8 9 10 11 |
KS Statistic P-Value Log_SalePrice 0.04261 0.00017 Sqrt_SalePrice 0.07689 0.00000 BoxCox_SalePrice 0.04294 0.00014 YeoJohnson_SalePrice 0.04294 0.00014 Quantile_SalePrice 0.00719 0.99924 Squared_YearBuilt 0.11661 0.00000 Cubed_YearBuilt 0.11666 0.00000 BoxCox_YearBuilt 0.11144 0.00000 YeoJohnson_YearBuilt 0.11144 0.00000 Quantile_YearBuilt 0.02243 0.14717 |
您可以看到,KS统计量越高,p值越低。相应地,
- KS统计量:这代表了样本的经验分布函数与参考分布的累积分布函数之间的最大差异。较小的值表示与正态分布的拟合度更好。
- P值:提供了在零假设下观察到测试结果的概率。较低的p值(通常<0.05)会拒绝零假设,表明样本分布与正态分布存在显著差异。
‘SalePrice’的分位数变换产生了最有希望的结果,KS统计量为0.00719,p值为0.99924,表明在此变换后,分布与正态分布非常接近。这并不奇怪,因为分位数变换的设计就是为了产生良好的拟合。p值很重要,因为较高的p值(接近1)表明无法拒绝零假设(即样本来自指定分布),这意味着良好的正态性。
其他变换,如Log、Box-Cox和Yeo-Johnson,也改善了‘SalePrice’的分布,但效果较小,这反映在它们较低的p值(范围从0.00014到0.00017)上,表明与分位数变换相比,与正态分布的符合度较低。应用于‘YearBuilt’的变换在实现正态性方面通常不如‘SalePrice’有效。BoxCox和YeoJohnson变换相比平方和立方提供了轻微的改进,这从它们稍低的KS统计量和p值可以看出,但仍然表明与正态性存在显著偏差。‘YearBuilt’的分位数变换显示出更有利的结果,KS统计量为0.02243,p值为0.14717,表明向正态性的中度改进,尽管不如对‘SalePrice’所示的效果明显。
选择正确的转换
选择正确的变换来处理数据的偏斜不是一刀切的决定;它需要仔细考虑数据的上下文和特征。在选择适当的变换方法时,上下文的重要性不容夸大。以下是需要考虑的关键因素:
- 数据特征:数据的性质(例如,零或负值的存在)可能会限制某些变换的适用性。例如,如果不进行调整,对零或负值无法直接进行对数变换。
- 偏斜程度:数据偏斜的程度会影响变换的选择。比轻微偏斜(可能用对数或平方根变换就足够了)更严重的偏斜可能需要更有效的变换(例如,Box-Cox或Yeo-Johnson)。
- 统计属性:选择的变换应能理想地改善数据集的统计属性,例如使分布正常化和稳定方差,这对于许多统计检验和模型至关重要。
- 可解释性:变换后结果的可解释性至关重要。一些变换,如对数或平方根,可以相对直接地解释,而另一些,如分位数变换,可能会使原始量表的解释复杂化。
- 分析目标:分析的最终目标——无论是预测建模、假设检验还是探索性分析——在选择变换方法时都起着至关重要的作用。变换应与稍后要使用的分析技术和模型保持一致。
总之,选择正确的变换取决于多种因素,包括但不限于对数据集的扎实理解、分析的具体目标以及对模型可解释性和性能的实际影响。没有一种方法是普遍优越的;每种方法都有其权衡和适用性,具体取决于当前的情况。需要强调的是,关于分位数变换,您的可视化和统计检验已将其确定为在实现正态分布方面非常有效。虽然它很强大,但分位数变换不是像其他变换那样的线性变换。这意味着它可能会以不易逆转的方式显著改变数据的结构,从而可能使结果的解释和反变换回原始量表的逆变换应用复杂化。因此,尽管它在正态化方面很有效,但应仔细考虑其使用,特别是在需要保持与原始数据量表的联系或模型可解释性是优先考虑的情况下。在大多数情况下,偏好可能倾向于在正态化有效性与简单性和可逆性之间取得平衡的变换,确保数据尽可能可解释和易于管理。
进一步阅读
API
- scipy.stats.boxcox API
- scipy.stats.yeojohnson API
- sklearn.preprocessing.Quantile Transformer API
- scipy.stats.kstest API
资源
总结
在本帖中,您深入探讨了数据变换,重点关注它们在数据科学领域处理偏斜数据中的关键作用。通过使用 Ames 住房数据集中的 'SalePrice' 和 'YearBuilt' 特征的实际示例,您演示了各种变换技术——对数、平方根、Box-Cox、Yeo-Johnson 和分位数变换——以及它们对数据分布正态化的影响。您的分析强调了根据数据特征、偏斜程度、统计目标、可解释性以及分析的具体目标选择适当变换的必要性。
具体来说,你学到了:
- 数据变换的重要性以及它们如何处理偏斜分布。
- 如何通过视觉和统计评估来比较不同变换的有效性。
- 评估数据特征、偏斜严重程度和分析目标以选择最合适的变换技术的重要性。
您有任何问题吗?请在下面的评论中提出您的问题,我将尽力回答。







暂无评论。