Transformer 模型由堆叠的 Transformer 层组成,每层都包含一个注意力子层和一个前馈子层。这些子层并非直接连接;相反,跳跃连接将输入与每个子层中处理过的输出相结合。在这篇文章中,您将探索 Transformer 模型中的跳跃连接。具体来说:
- 为什么跳跃连接对于训练深度 Transformer 模型至关重要
- 残差连接如何实现梯度流动并防止梯度消失
- 预归一化(pre-norm)和后归一化(post-norm)Transformer 架构之间的区别
让我们开始吧。

Transformer 模型中的跳跃连接
图片由 David Emrich 拍摄。保留部分权利。
概述
这篇博文分为三部分;它们是:
- Transformer 中为何需要跳跃连接
- Transformer 模型中跳跃连接的实现
- 预归一化与后归一化 Transformer 架构
Transformer 中为何需要跳跃连接
Transformer 模型与其他深度学习模型一样,将许多层堆叠在一起。随着层数的增加,由于梯度消失问题,训练变得越来越困难。当梯度反向传播通过许多层时,它们会呈指数级减小,使得早期层几乎不可能有效学习。
成功深度学习模型的关键是保持良好的梯度流动。跳跃连接,也称为残差连接,为信息和梯度流经网络创建了直接路径。它们允许模型学习残差函数,即期望输出与输入之间的差异,而不是从头开始学习完整的转换。这个概念首次在 ResNet 论文中提出。数学上,这意味着:
$$y = F(x) + x$$
其中函数 $F(x)$ 是学习得到的。请注意,将 $F(x) = 0$ 设置为使输出 $y$ 等于输入 $x$。这称为**恒等映射**。从这个基线开始,模型可以逐渐使 $y$ 偏离 $x$,而不是寻找一个全新的函数 $F(x)$。这就是使用跳跃连接的动机。
在反向传播期间,关于输入的梯度变为:
$$\frac{\partial L}{\partial x} = \frac{\partial L}{\partial y} \cdot \frac{\partial y}{\partial x} = \frac{\partial L}{\partial y} \cdot \left(\frac{\partial F(x)}{\partial x} + 1\right)$$
“+1”项确保即使当 $\partial F/\partial x$ 很小,梯度也不会减小。这就是跳跃连接缓解梯度消失问题的原因。
在 Transformer 模型中,跳跃连接应用于每个子层(注意力层和前馈网络)。这种设计为梯度反向流动提供了路径,使 Transformer 模型能够更快地收敛:鉴于其通常很深的架构和漫长的训练时间,这是一个关键优势。
下图说明了典型的跳跃连接用法:
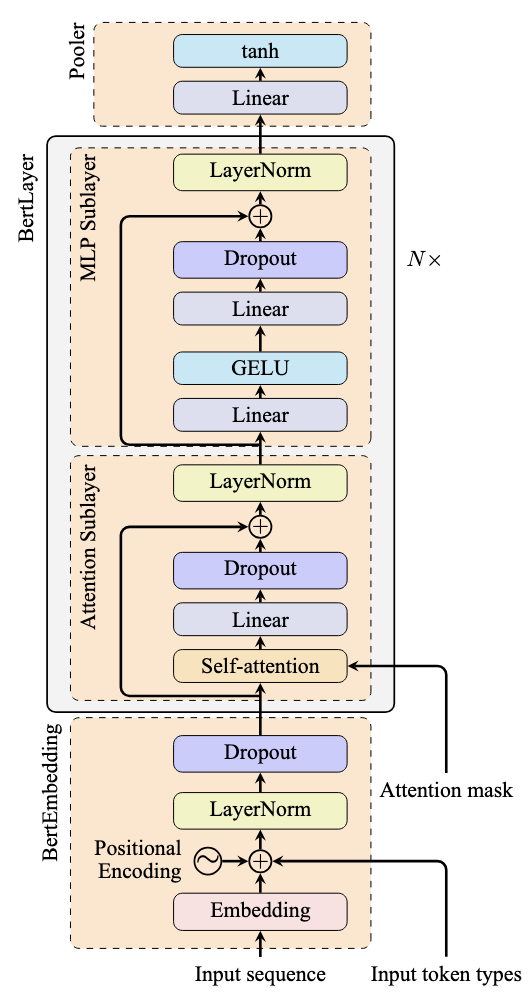
请注意箭头如何表示绕过注意力子层和前馈子层的跳跃连接。这些连接将输入直接添加到每个子层的输出,从而创建残差学习框架。
Transformer 模型中跳跃连接的实现
以下是 Transformer 模型中残差连接的典型实现方式:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
import torch.nn as nn class BertLayer(nn.Module): def __init__(self, dim, intermediate_dim, num_heads): super().__init__() self.attention = nn.MultiheadAttention(dim, num_heads) self.linear1 = nn.Linear(dim, intermediate_dim) self.linear2 = nn.Linear(intermediate_dim, dim) self.act = nn.GELU() self.norm1 = nn.LayerNorm(dim) self.norm2 = nn.LayerNorm(dim) def forward(self, x): # 注意力子层周围的跳跃连接 attn_output = self.attention(x, x, x)[0] # 提取元组的第一个元素 x = x + attn_output # 残差连接 x = self.norm1(x) # 层归一化 # MLP 子层周围的跳跃连接 mlp_output = self.linear1(x) mlp_output = self.act(mlp_output) mlp_output = self.linear2(mlp_output) x = x + mlp_output # 残差连接 x = self.norm2(x) # 层归一化 return x |
这个 PyTorch 实现代表了 BERT 模型的一层,如上图所示。`nn.MultiheadAttention` 模块取代了注意力子层中的自注意力层和线性层。
在 `forward()` 方法中,注意力模块的输出保存为 `attn_output`,并在应用层归一化之前添加到输入 `x`。这种添加实现了跳跃连接。类似地,在 MLP 子层中,输入 `x`(MLP 子层的输入,而不是整个 Transformer 层)被添加到 `mlp_output`。
预归一化与后归一化 Transformer 架构
层归一化相对于跳跃连接的放置显著影响训练稳定性和模型性能。出现了两种主要架构:预归一化(pre-norm)和后归一化(post-norm)Transformer。
最初的“Attention Is All You Need”论文使用了后归一化架构,其中层归一化在残差连接之后应用。上面的代码实现了后归一化架构,在跳跃连接添加之后应用归一化。
大多数现代 Transformer 模型都使用预归一化架构,其中归一化在子层之前应用:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
class PreNormTransformerLayer(nn.Module): def __init__(self, dim, intermediate_dim, num_heads): super().__init__() self.attention = nn.MultiheadAttention(dim, num_heads) self.linear1 = nn.Linear(dim, intermediate_dim) self.linear2 = nn.Linear(intermediate_dim, dim) self.act = nn.GELU() self.norm1 = nn.LayerNorm(dim) self.norm2 = nn.LayerNorm(dim) def forward(self, x): # 预归一化:在子层之前进行归一化 normalized_x = self.norm1(x) attn_output = self.attention(normalized_x, normalized_x, normalized_x)[0] x = x + attn_output # 残差连接 normalized_x = self.norm2(x) mlp_output = self.linear1(normalized_x) mlp_output = self.act(mlp_output) mlp_output = self.linear2(mlp_output) x = x + mlp_output # 残差连接 return x |
在这个预归一化实现中,归一化应用于输入 `x`,在注意力层和 MLP 操作之前,之后再应用跳跃连接。
预归一化和后归一化架构之间的选择会影响训练和性能:
- 训练稳定性:后归一化在训练期间可能不稳定,特别是对于非常深的模型,因为梯度方差会随深度呈指数级增长。预归一化模型训练起来更稳健。
- 收敛速度:预归一化模型通常收敛更快,并且对学习率选择的敏感度较低。后归一化模型需要精心设计的学习率调度和热身期。
- 模型性能:尽管存在训练挑战,后归一化模型在成功训练后通常表现更好。
大多数现代 Transformer 模型都使用预归一化架构,因为它们太深太大。在这些情况下,更快的收敛比略微更好的性能更有价值。
进一步阅读
以下是一些您可能会觉得有用的资源:
- 用于图像识别的深度残差学习
- 关于 Transformer 架构中的层归一化
- 理解训练深度前馈神经网络的难度
- BERT:用于语言理解的深度双向 Transformer 预训练
- LLaMA:开放高效的基础语言模型
- PyTorch MultiheadAttention API 文档
总结
在这篇文章中,您了解了 Transformer 模型中的跳跃连接。具体来说,您了解了:
- 为什么跳跃连接对于训练深度 Transformer 模型至关重要
- 残差连接如何实现梯度流动并防止梯度消失
- 预归一化(pre-norm)和后归一化(post-norm)Transformer 架构之间的区别
- 根据您的具体要求何时使用每种架构变体
跳跃连接是实现深度 Transformer 模型训练的基础组件。预归一化和后归一化架构之间的选择会显著影响训练稳定性和模型性能,其中预归一化是大多数现代应用程序的首选。






暂无评论。