使用 Python 的 Softmax 激活函数

作者 Jason Brownlee 于 2020年6月24日发布在深度学习 19

Softmax 是一种数学函数，它将一个数字向量转换为一个概率向量，其中每个值的概率与其在向量中的相对大小成正比。

在应用机器学习中，softmax 函数最常见的用途是作为神经网络模型中的激活函数。具体来说，模型被配置为输出 N 个值，每个值对应于分类任务中的一个类别，然后使用 softmax 函数对输出进行归一化，将它们从加权和值转换为总和为一的概率。softmax 函数输出中的每个值都被解释为每个类别的成员概率。

在本教程中，您将了解神经网络模型中使用的 softmax 激活函数。

完成本教程后，您将了解：

线性激活函数和 Sigmoid 激活函数不适用于多类别分类任务。
Softmax 可以被看作是 argmax 函数的一个“软化”版本，argmax 函数返回列表中最大值的索引。
如何从头开始在 Python 中实现 softmax 函数，以及如何将输出转换为类别标签。

让我们开始吧。

使用 Python 的 Softmax 激活函数
照片作者：Ian D. Keating，部分权利保留。

教程概述

本教程分为三个部分；它们是：

使用神经网络预测概率
最大值、argmax 和 Softmax
Softmax 激活函数

使用神经网络预测概率

神经网络模型可用于模拟分类预测建模问题。

分类问题是指预测给定输入的类别标签的问题。模拟分类问题的标准方法是使用模型来预测类别成员的概率。也就是说，给定一个样本，它属于每个已知类别标签的概率是多少？

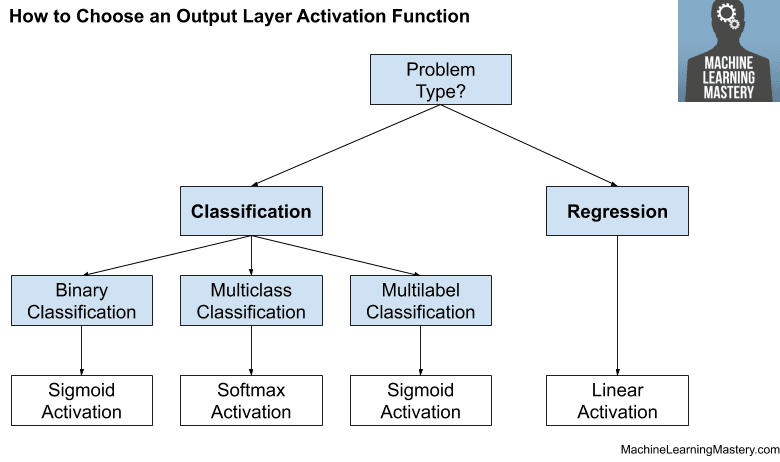
对于二元分类问题，可以使用二项概率分布。这通过在输出层具有单个节点来完成，该节点预测样本属于类别 1 的概率。
对于多类别分类问题，可以使用多项概率。这通过在输出层为每个类别具有一个节点来完成，并且预测概率的总和等于一。

神经网络模型需要在模型输出层中使用激活函数来进行预测。

有不同的激活函数可供选择；让我们看几个。

线性激活函数

预测类别成员概率的一种方法是使用线性激活。

线性激活函数就是节点加权输入的总和，它是任何激活函数所必需的输入。因此，它通常被称为“*无激活函数*”，因为它没有进行额外的转换。

回想一下，概率或似然性是介于 0 和 1 之间的数值。

鉴于对输入加权总和没有进行任何转换，线性激活函数有可能输出任何数值。这使得线性激活函数不适用于二项或多项情况的概率预测。

Sigmoid 激活函数

预测类别成员概率的另一种方法是使用 sigmoid 激活函数。

该函数也称为逻辑函数。无论输入如何，该函数始终输出介于 0 和 1 之间的值。该函数的形式是介于 0 和 1 之间的 S 形，其垂直线或“S”的中间值为 0.5。

这使得非常大的输入加权总和可以输出为 1.0，而非常小或负的值则映射到 0.0。

sigmoid 激活函数是二元分类问题的理想激活函数，其中输出被解释为二项概率分布。

sigmoid 激活函数也可以用作多标签分类（而非多类别分类）问题的激活函数，其中类别是非互斥的。

sigmoid 激活函数不适用于需要多项概率分布的互斥类别的多类别分类问题。

相反，需要一个称为 **softmax 函数** 的替代激活。

最大值、argmax 和 Softmax

最大值函数

最大值或“*max*”数学函数返回数字值列表中的最大数值。

我们可以使用 `max()` Python 函数来实现它；例如

# example of the max of a list of numbers
# define data
data = [1, 3, 2]
# calculate the max of the list
result = max(data)
print(result)

# 示例：列表数字的最大值

# 定义数据

data = [1, 3, 2]

# 计算列表的最大值

result = max(data)

print(result)

运行该示例，返回数字列表中的最大值“3”。

3

Argmax 函数

argmax 或“*arg max*”数学函数返回包含最大值的列表中的索引。

可以将其视为 max 的元版本：比 max 高一个层次，指向列表中具有最大值的那个位置，而不是值本身。

我们可以使用 argmax() NumPy 函数来实现它；例如

# example of the argmax of a list of numbers
from numpy import argmax
# define data
data = [1, 3, 2]
# calculate the argmax of the list
result = argmax(data)
print(result)

# 示例：列表数字的 argmax

from numpy import argmax

# 定义数据

data = [1, 3, 2]

# 计算列表的 argmax

result = argmax(data)

print(result)

运行该示例，返回列表索引值“1”，它指向数组索引 [1]，该索引包含列表中最大的值“3”。

1

Softmax 函数

softmax 或“*soft max*”数学函数可以被认为是 argmax 函数的概率或“*更软*”的版本。

使用 softmax 这个术语是因为该激活函数表示了“赢家通吃”激活模型的平滑版本，其中输入最大的单元输出为 +1，而所有其他单元输出为 0。

— 第 238 页，《Neural Networks for Pattern Recognition》，1995。

从概率的角度来看，如果在上一节中 `argmax()` 函数返回 1，那么它会为其他两个数组索引返回 0，将所有权重赋予索引 1，将权重赋予索引 0 和索引 2 为 0，以获得列表 [1, 3, 2] 中的最大值。

[0, 1, 0]

[0, 1, 0]

如果我们不太确定，并想以概率方式表达 argmax，赋予权重，该怎么办？

这可以通过缩放列表中的值并将它们转换为概率来实现，使得返回列表中的所有值加起来等于 1.0。

这可以通过计算列表中每个值的指数，然后除以指数值之和来实现。

概率 = exp(值) / sum v in list exp(v)

例如，我们可以如下将列表 [1, 3, 2] 中的第一个值“1”转换为概率

概率 = exp(1) / (exp(1) + exp(3) + exp(2))
概率 = exp(1) / (exp(1) + exp(3) + exp(2))
概率 = 2.718281828459045 / 30.19287485057736
概率 = 0.09003057317038046

我们可以如下在 Python 中为列表 [1, 3, 2] 中的每个值演示这一点

# transform values into probabilities
from math import exp
# calculate each probability
p1 = exp(1) / (exp(1) + exp(3) + exp(2))
p2 = exp(3) / (exp(1) + exp(3) + exp(2))
p3 = exp(2) / (exp(1) + exp(3) + exp(2))
# report probabilities
print(p1, p2, p3)
# report sum of probabilities
print(p1 + p2 + p3)

# 将值转换为概率

from math import exp

# 计算每个概率

p1 = exp(1) / (exp(1) + exp(3) + exp(2))

p2 = exp(3) / (exp(1) + exp(3) + exp(2))

p3 = exp(2) / (exp(1) + exp(3) + exp(2))

# 报告概率

print(p1, p2, p3)

# 报告概率之和

print(p1 + p2 + p3)

运行该示例将每个值转换为概率并报告这些值，然后确认所有概率的总和为 1.0。

我们可以看到，权重最大的是索引 1（67%），其次是索引 2（24%），索引 0 的权重更少（9%）。

0.09003057317038046 0.6652409557748219 0.24472847105479767
1.0

1 2	0.09003057317038046 0.6652409557748219 0.24472847105479767 1.0

这就是 softmax 函数。

我们可以将其实现为一个函数，该函数接受一个数字列表并返回该列表的 softmax 或多项概率分布。

下面的示例实现了该函数，并在我们的小数字列表上进行了演示。

# example of a function for calculating softmax for a list of numbers
from numpy import exp

# calculate the softmax of a vector
def softmax(vector):
	e = exp(vector)
	return e / e.sum()

# define data
data = [1, 3, 2]
# convert list of numbers to a list of probabilities
result = softmax(data)
# report the probabilities
print(result)
# report the sum of the probabilities
print(sum(result))

# 示例：计算数字列表 softmax 的函数

from numpy import exp

# 计算向量的 softmax

def softmax(vector):

e = exp(vector)

return e / e.sum()

# 定义数据

data = [1, 3, 2]

# 将数字列表转换为概率列表

result = softmax(data)

# 报告概率

print(result)

# 报告概率之和

print(sum(result))

运行该示例，再次得到大致相同的数字，精度略有差异。

[0.09003057 0.66524096 0.24472847]
1.0

1 2	[0.09003057 0.66524096 0.24472847] 1.0

最后，我们可以使用内置的 softmax() NumPy 函数来计算数组或数字列表的 softmax，如下所示

# example of calculating the softmax for a list of numbers
from scipy.special import softmax
# define data
data = [1, 3, 2]
# calculate softmax
result = softmax(data)
# report the probabilities
print(result)
# report the sum of the probabilities
print(sum(result))

# 示例：计算数字列表的 softmax

from scipy.special import softmax

# 定义数据

data = [1, 3, 2]

# 计算 softmax

result = softmax(data)

# 报告概率

print(result)

# 报告概率之和

print(sum(result))

运行示例，同样，我们得到非常相似的结果，精度差异非常小。

[0.09003057 0.66524096 0.24472847]
0.9999999999999997

1 2	[0.09003057 0.66524096 0.24472847] 0.9999999999999997

现在我们已经熟悉了 softmax 函数，让我们看看它在神经网络模型中的用法。

Softmax 激活函数

softmax 函数用作预测多项概率分布的神经网络模型输出层中的激活函数。

也就是说，softmax 用作多类别分类问题的激活函数，其中类别成员资格需要两个以上的类别标签。

任何时候我们希望表示具有 n 个可能值的离散变量的概率分布，我们都可以使用 softmax 函数。这可以看作是 sigmoid 函数的泛化，sigmoid 函数用于表示二元变量的概率分布。

— 第 184 页，《Deep Learning》，2016。

该函数可以用作神经网络隐藏层的激活函数，尽管这不太常见。当模型内部需要在瓶颈或连接层选择或加权多个不同输入时，可以使用它。

Softmax 单元自然地表示了具有 k 个可能值的离散变量的概率分布，因此它们可用作一种开关。

— 第 196 页，《Deep Learning》，2016。

在 Keras 深度学习库中，对于三类分类任务，在输出层使用 softmax 可能如下所示

...
model.add(Dense(3, activation='softmax'))

1 2	... model.add(Dense(3, activation='softmax'))

根据定义，softmax 激活将为输出层中的每个节点输出一个值。输出值将表示（或可解释为）概率，并且这些值的总和为 1.0。

在对多类别分类问题进行建模时，必须准备数据。包含类别标签的目标变量首先被进行标签编码，这意味着为每个类别标签分配一个从 0 到 N-1 的整数，其中 N 是类别标签的数量。

然后对标签编码（或整数编码）的目标变量进行独热编码。这是一种概率表示的类别标签，非常类似于 softmax 的输出。创建一个向量，其中包含每个类别标签的位置。所有值标记为 0（不可能），而 1（确定）用于标记类别标签的位置。

例如，三个类别标签将被整数编码为 0、1 和 2。然后编码为向量，如下所示

类别 0: [1, 0, 0]
类别 1: [0, 1, 0]
类别 2: [0, 0, 1]

这被称为独热编码。

它代表了用于在有监督学习中纠正模型的每个类别的预期多项概率分布。

softmax 函数将为每个类别标签输出类别成员的概率，并尝试最好地近似给定输入的预期目标。

例如，如果一个样本预期是整数编码的类别 1，则目标向量将是

[0, 1, 0]

softmax 输出可能如下所示，它将最大的权重放在类别 1 上，而将较小的权重放在其他类别上。

[0.09003057 0.66524096 0.24472847]

预期的多项概率分布与预测的多项概率分布之间的误差通常使用交叉熵来计算，然后使用该误差来更新模型。这称为交叉熵损失函数。

有关使用交叉熵计算概率分布之间差异的更多信息，请参阅本教程

机器学习交叉熵简明介绍

我们可能需要将概率转换回整数编码的类别标签。

这可以通过 `argmax()` 函数来实现，该函数返回列表中具有最大值的索引。鉴于类别标签是从 0 到 N-1 进行整数编码的，概率的 argmax 始终是整数编码的类别标签。

类别整数 = argmax([0.09003057 0.66524096 0.24472847])
类别整数 = 1

进一步阅读

如果您想深入了解，本节提供了更多关于该主题的资源。

书籍

《用于模式识别的神经网络》, 1995.
Neural Networks: Tricks of the Trade: Tricks of the Trade, 第二版，2012。
深度学习, 2016.

API

文章

Softmax 函数，维基百科.

总结

在本教程中，您了解了神经网络模型中使用的 softmax 激活函数。

具体来说，你学到了：

线性激活函数和 Sigmoid 激活函数不适用于多类别分类任务。
Softmax 可以被看作是 argmax 函数的一个“软化”版本，argmax 函数返回列表中最大值的索引。
如何从头开始在 Python 中实现 softmax 函数，以及如何将输出转换为类别标签。

你有什么问题吗？
在下面的评论中提出你的问题，我会尽力回答。

关于此主题的更多信息

如何在 Python 中开发 LARS 回归模型

6 本关于集成学习的书

对 Softmax Activation Function with Python 的 19 条回复

Deepak 2020年10月19日上午6:56 #

Jason，问问 softmax 是否能产生校准良好的概率，这是一个公平的问题吗？或者应该问，特定的神经网络架构是否会产生校准良好的概率？无论如何，是否存在理论上预期能获得校准良好概率的情况或算法？

回复
- Jason Brownlee 2020年10月19日上午7:42 #
  
  总的来说，我相信 MLP 的概率校准得不好。
  
  回复
Markus 2020年10月21日上午1:10 #

嗨

感谢这篇好文章。

在这篇文章中，也许也值得一提的是在处理大数（或大负数）时可能遇到的数值稳定性问题，以及在这种情况下解决方案是什么，比如您的示例

data = [1000, 3000, 2000]

回复
- Jason Brownlee 2020年10月21日上午6:41 #
  
  感谢您的建议。
  
  回复
Mohammed 2020年10月23日下午3:06 #

根据这两篇论文，softmax 函数的输出值不能用作置信度 1) https://arxiv.org/pdf/1706.04599.pdf 2) https://ieeexplore.ieee.org/document/9156634

回复
- Jason Brownlee 2020年10月24日上午6:53 #
  
  是的，这众所周知。谢谢分享。尽管如此，它在实践中是一个有用的代理。
  
  回复
Benjamin 2020年12月30日下午4:23 #

嗨，Jason，

感谢这篇关于激活函数的精彩文章！

我最近一直在研究输出层上的多标签分类。

我偶然发现了这篇关于 n 元激活函数的博客文章！

https://r2rt.com/beyond-binary-ternary-and-one-hot-neurons.html

我有 15 个输出神经元，每个神经元可以是 1、0 或 -1。彼此独立。

我过去会采用 tanh 激活函数，并将神经元划分为 3 个区间（x < -0.5，-0.5 < x <= 0.5，x > 0.5）来决定每个神经元预测后的类别。

我认为新建议的方法将使划分更有意义！

或者您认为我应该对我的系统进行独热编码，以便一个神经元只能具有值 0 或 1，然后使用 sigmoid？

许多问候！

回复
- Benjamin 2020年12月30日下午5:19 #
  
  *忘了写“x>0.5”
  
  回复
- Jason Brownlee 2020年12月31日上午5:20 #
  
  不客气。
  
  很难说。也许你可以评估几种不同的方法，看看哪种最适合你的特定数据集。
  
  回复
Karis 2021年3月4日下午4:40 #

只是来感谢您所有的文章和教程。作为一名年轻的数据分析师和 Python 程序员，我经常来阅读您的文章，因为您解释得很好。谢谢！

回复
- Jason Brownlee 2021年3月5日上午5:31 #
  
  不客气，谢谢您的美言！
  
  回复
Mattias 2021年3月26日下午4:33 #

嗨，Jason，

很棒的教程网站。谢谢。
我想知道 softmax 用于二元分类有多大意义？例如，如果我们想让 CNN 学习关于猫和狗，它最终会理解“如果它不是狗，那就是猫。”，而无需学习猫的特征。

回复
- Jason Brownlee 2021年3月29日上午5:50 #
  
  Softmax 不用于二元分类问题，您应该使用 sigmoid。
  
  回复
Aira 2022年4月17日上午1:58 #

你好，Jason！
谢谢分享激活函数。您的解释非常好，易于理解。但我有一个问题。您说过

“对目标变量进行标签编码（或整数编码），然后进行独热编码。对目标变量进行标签编码（或整数编码），然后进行独热编码。”

我们放到数据集中的目标标签是整数编码（0 到 N-1）还是独热编码？

回复
- James Carmichael 2022年4月17日上午7:58 #
  
  嗨 Aira…它们是独热编码的。
  
  回复
Aarti Gehani 2022年11月16日上午7:31 #

嗨，Jason，

感谢这篇精彩的文章。确实很容易理解。

我是 ML 领域的新手，想知道您是如何打印出 softmax 输出的 [0.09003057 0.66524096 0.24472847] 值的？是紧接着模型的最后一层打印的，还是您编译-拟合-评估-预测然后打印了预测值？

谢谢。

回复
- James Carmichael 2022年11月17日上午9:43 #
  
  嗨 Aarti…它们是最终的预测值。
  
  回复
JeffR 2023年11月23日上午8:07 #

我注意到 logsoftmax 目前比 softmax 激活函数更受青睐。然而，由于 logsoftmax 具有线性传递函数（它是反 log 的 log），它等同于施加增益。这有什么价值？

回复
- James Carmichael 2023年11月23日上午9:49 #
  
  嗨 JeffR…以下资源可能对您感兴趣。
  
  https://medium.com/@AbhiramiVS/softmax-vs-logsoftmax-eb94254445a2
  
  回复

导航

使用 Python 的 Softmax 激活函数

教程概述

使用神经网络预测概率

线性激活函数

Sigmoid 激活函数

最大值、argmax 和 Softmax

最大值函数

Argmax 函数

Softmax 函数

Softmax 激活函数

进一步阅读

书籍

API

文章

总结

关于此主题的更多信息

对 Softmax Activation Function with Python 的 19 条回复

发表回复点击此处取消回复。

导航

教程概述

使用神经网络预测概率

线性激活函数

Sigmoid 激活函数

最大值、argmax 和 Softmax

最大值函数

Argmax 函数

Softmax 函数

Softmax 激活函数

进一步阅读

书籍

API

文章

总结

关于此主题的更多信息

对 *Softmax Activation Function with Python* 的 19 条回复

发表回复 点击此处取消回复。

对 Softmax Activation Function with Python 的 19 条回复

发表回复点击此处取消回复。