线性回归是一种用于建模一个或多个自变量与因变量之间关系的方法。
它是统计学中的一个重要组成部分,通常被认为是入门级的机器学习方法。它也可以用矩阵表示法进行重构,并使用矩阵运算来求解。
在本教程中,您将了解线性回归的矩阵形式以及如何使用直接法和矩阵分解法来求解。
完成本教程后,您将了解:
- 线性回归与法方程的矩阵重构。
- 如何使用 QR 矩阵分解求解线性回归。
- 如何使用 SVD 和伪逆求解线性回归。
启动您的项目,阅读我的新书《机器学习线性代数》,其中包含分步教程和所有示例的Python源代码文件。
让我们开始吧。

如何使用线性代数解决线性回归
照片由 likeaduck 提供,保留部分权利。
教程概述
本教程分为6个部分;它们是
- 线性回归
- 线性回归的矩阵形式
- 线性回归数据集
- 直接求解
- 通过 QR 分解求解
- 通过奇异值分解求解
在机器学习线性代数方面需要帮助吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
线性回归
线性回归是一种用于建模两个标量值之间关系的方法:输入变量 x 和输出变量 y。
该模型假设 y 是输入变量的线性函数或加权和。
|
1 |
y = f(x) |
或者,用系数表示。
|
1 |
y = b0 + b1 . x1 |
该模型还可以用于模拟给定多个输入变量(称为多元线性回归)的输出变量(如下所示,为便于阅读添加了括号)。
|
1 |
y = b0 + (b1 . x1) + (b2 . x2) + ... |
创建线性回归模型的目标是找到系数(b)的值,以最小化输出变量 y 预测中的误差。
线性回归的矩阵形式
线性回归可以用矩阵表示法表示;例如
|
1 |
y = X . b |
或者,不使用点符号。
|
1 |
y = Xb |
其中 X 是输入数据,每一列是一个数据特征,b 是系数向量,y 是 X 中每一行的输出变量向量。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
x11, x12, x13 X = (x21, x22, x23) x31, x32, x33 x41, x42, x43 b1 b = (b2) b3 y1 y = (y2) y3 y4 |
重构后,问题变成了一个线性方程组,其中 b 向量的值是未知的。这种类型的系统被称为超定系统,因为未知数的方程数量多于未知数,即每个系数都用于数据行中的每一行。
由于存在多个不一致的解(例如,系数有多个可能的值),因此解析求解该问题具有挑战性。此外,所有解都会有某些误差,因为没有一条直线可以穿过几乎所有点,因此求解方程的方法必须能够处理这种情况。
通常通过找到模型中 b 的值最小化平方误差的解来实现。这被称为线性最小二乘法。
|
1 |
||X . b - y||^2 = sum i=1 to m ( sum j=1 to n Xij . bj - yi)^2 |
只要输入列是独立的(例如,不相关),这种形式就有唯一的解。
我们不能总是将误差 e = b – Ax 降到零。当 e 为零时,x 是 Ax = b 的精确解。当 e 的长度尽可能小时,xhat 是最小二乘解。
— 第 219 页,《线性代数导论》,第五版,2016。
在矩阵表示法中,该问题使用所谓的法方程进行表述
|
1 |
X^T . X . b = X^T . y |
可以重新排列以指定 b 的解为
|
1 |
b = (X^T . X)^-1 . X^T . y |
这可以直接求解,但考虑到矩阵逆的存在,可能在计算上具有挑战性或不稳定。
线性回归数据集
为了探讨线性回归的矩阵形式,我们首先定义一个数据集作为上下文。
我们将使用一个简单的二维数据集,该数据集易于在散点图上可视化,并且模型易于可视化为试图拟合数据点的直线。
下面的示例定义了一个 5x2 的矩阵数据集,将其拆分为 X 和 y 分量,并绘制了数据集的散点图。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
from numpy import array from matplotlib import pyplot data = array([ [0.05, 0.12], [0.18, 0.22], [0.31, 0.35], [0.42, 0.38], [0.5, 0.49], ]) print(data) X, y = data[:,0], data[:,1] X = X.reshape((len(X), 1)) # 绘制数据集 pyplot.scatter(X, y) pyplot.show() |
运行此示例首先打印定义的数据集。
|
1 2 3 4 5 |
[[ 0.05 0.12] [ 0.18 0.22] [ 0.31 0.35] [ 0.42 0.38] [ 0.5 0.49]] |
将创建数据集的散点图,显示一条直线无法精确拟合此数据。
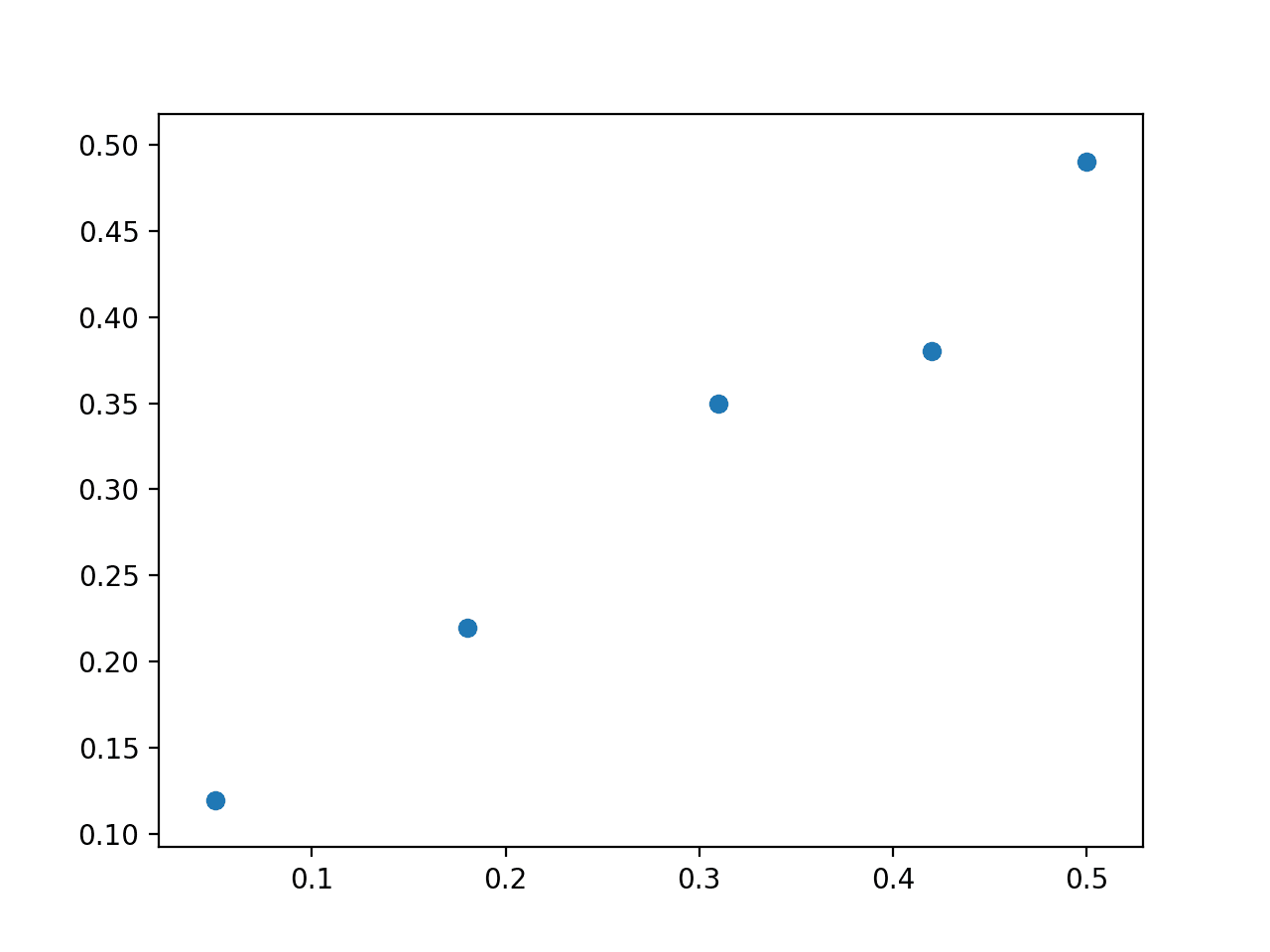
线性回归数据集散点图
直接求解
第一种方法是尝试直接求解回归问题。
也就是说,给定 X,哪些系数 b 的集合与 X 相乘会得到 y。正如我们在前面部分所看到的,法方程定义了如何直接计算 b。
|
1 |
b = (X^T . X)^-1 . X^T . y |
这可以使用 NumPy 中的 inv() 函数直接计算,该函数用于计算矩阵的逆。
|
1 |
b = inv(X.T.dot(X)).dot(X.T).dot(y) |
一旦计算出系数,我们就可以使用它们根据 X 来预测结果。
|
1 |
yhat = X.dot(b) |
将此与上一节定义的数据集结合起来,完整的示例如下。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
# 直接求解 from numpy import array from numpy.linalg import inv from matplotlib import pyplot data = array([ [0.05, 0.12], [0.18, 0.22], [0.31, 0.35], [0.42, 0.38], [0.5, 0.49], ]) X, y = data[:,0], data[:,1] X = X.reshape((len(X), 1)) # 线性最小二乘法 b = inv(X.T.dot(X)).dot(X.T).dot(y) print(b) # 使用系数进行预测 yhat = X.dot(b) # 绘制数据和预测 pyplot.scatter(X, y) pyplot.plot(X, yhat, color='red') pyplot.show() |
运行此示例将执行计算并打印系数向量 b。
|
1 |
[ 1.00233226] |
然后将创建数据集的散点图,其中包含模型的线图,显示出对数据的合理拟合。
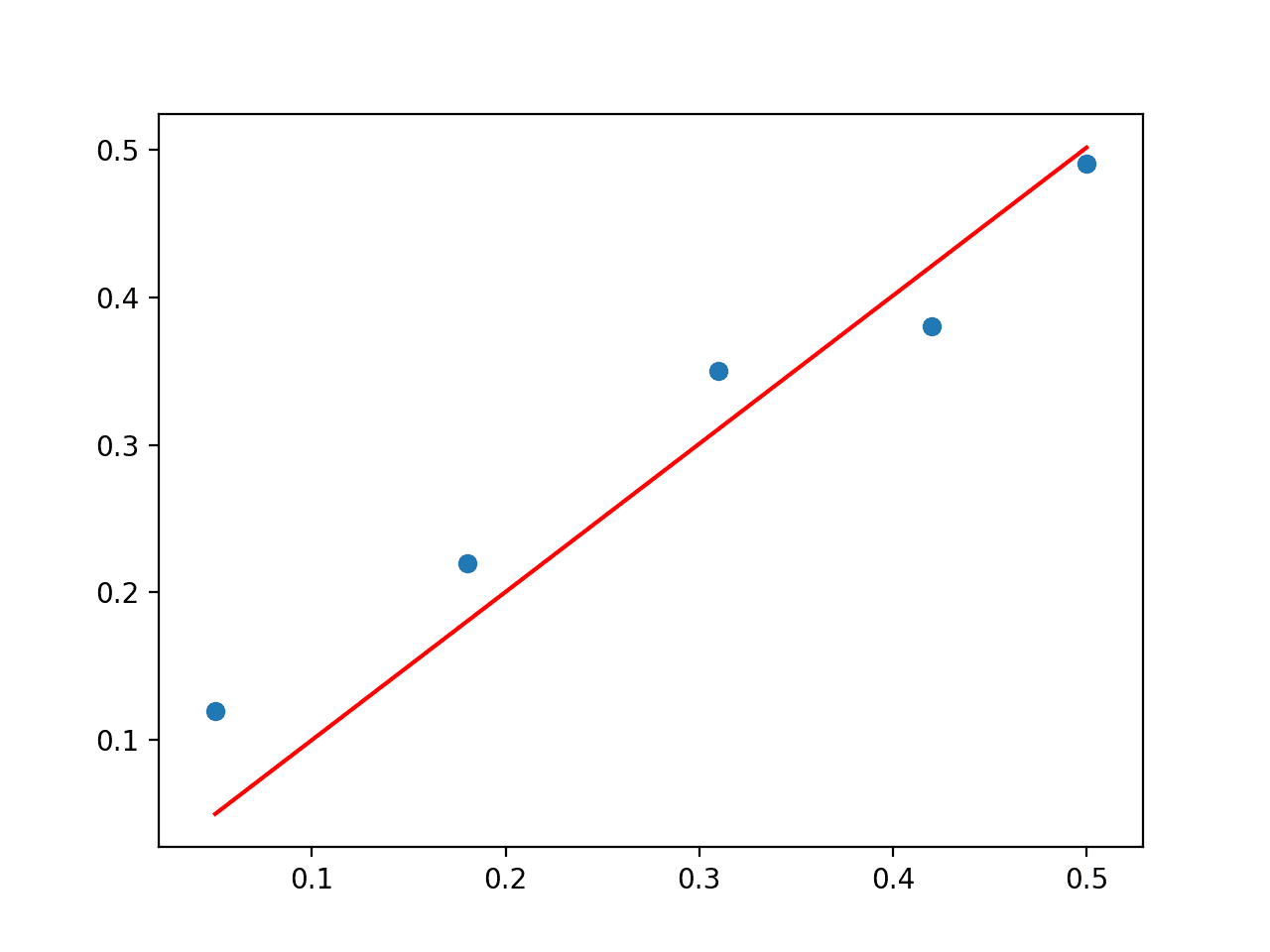
线性回归问题直接解的散点图
这种方法的问题在于矩阵求逆,它既耗费计算资源又不稳定。另一种方法是使用矩阵分解来避免此操作。我们将在以下几节中探讨两个示例。
通过 QR 分解求解
QR 分解是将矩阵分解为其组成元素的方法。
|
1 |
A = Q . R |
其中 A 是我们要分解的矩阵,Q 是一个 m x m 矩阵,R 是一个 m x n 的上三角矩阵。
QR 分解是求解线性最小二乘方程的一种流行方法。
跳过所有推导,系数可以使用 Q 和 R 元素如下找到
|
1 |
b = R^-1 . Q.T . y |
这种方法仍然涉及矩阵求逆,但在此情况下仅对更简单的 R 矩阵进行。
可以使用 NumPy 中的 qr() 函数找到 QR 分解。NumPy 中系数的计算如下所示
|
1 2 3 |
# QR 分解 Q, R = qr(X) b = inv(R).dot(Q.T).dot(y) |
将此与数据集结合起来,完整的示例如下。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
# 通过 QR 分解进行最小二乘法 from numpy import array from numpy.linalg import inv from numpy.linalg import qr from matplotlib import pyplot data = array([ [0.05, 0.12], [0.18, 0.22], [0.31, 0.35], [0.42, 0.38], [0.5, 0.49], ]) X, y = data[:,0], data[:,1] X = X.reshape((len(X), 1)) # QR 分解 Q, R = qr(X) b = inv(R).dot(Q.T).dot(y) print(b) # 使用系数进行预测 yhat = X.dot(b) # 绘制数据和预测 pyplot.scatter(X, y) pyplot.plot(X, yhat, color='red') pyplot.show() |
运行此示例将首先打印系数解,并绘制带有模型的图。
|
1 |
[ 1.00233226] |
QR 分解方法比直接计算法方程在计算上更有效率,在数值上更稳定,但并非适用于所有数据矩阵。
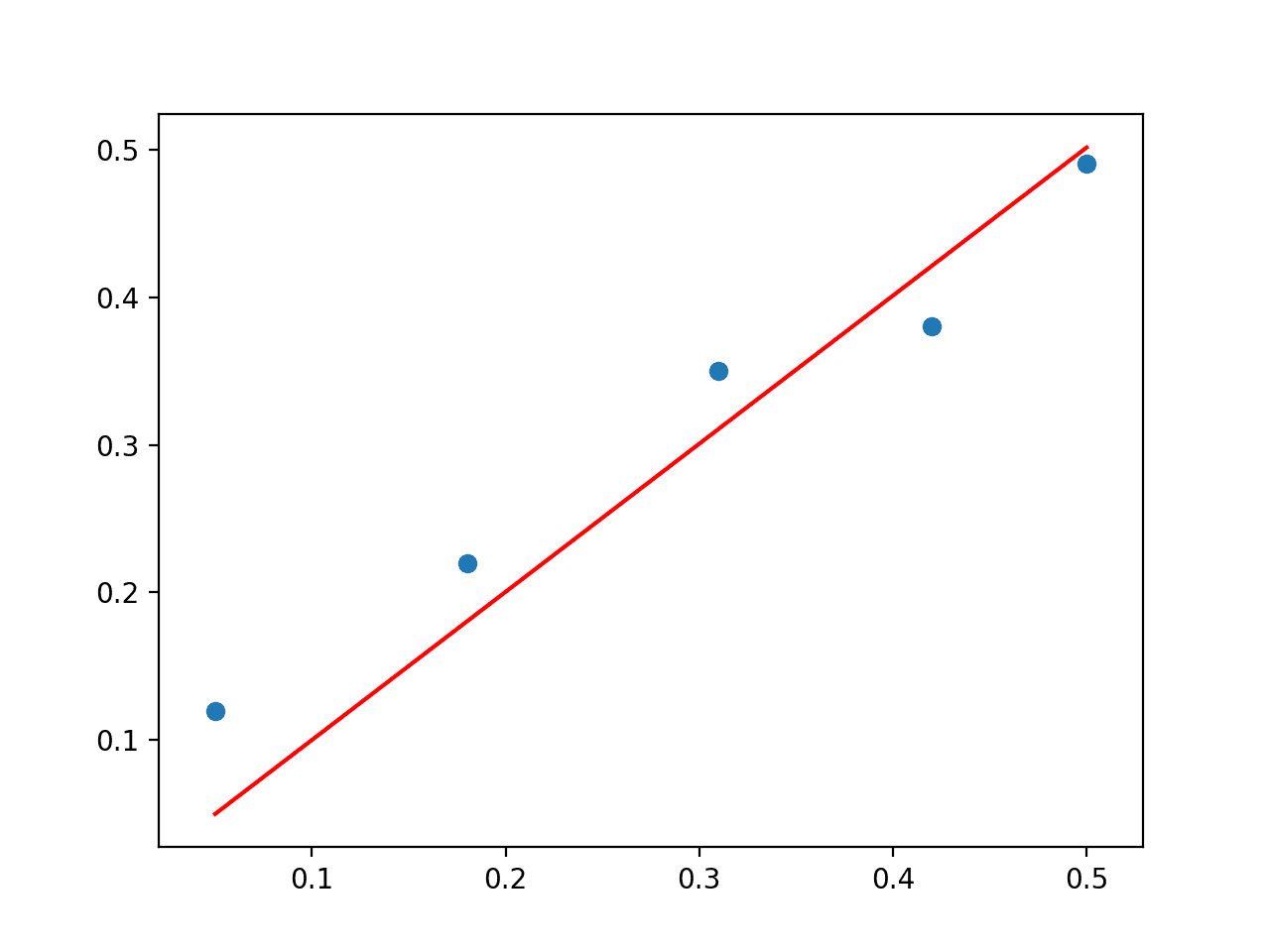
线性回归问题 QR 分解解的散点图
通过奇异值分解求解
奇异值分解(Singular-Value Decomposition),简称 SVD,与 QR 分解一样,是一种矩阵分解方法。
|
1 |
X = U . Sigma . V^* |
其中 A 是我们要分解的实数 n x m 矩阵,U 是一个 m x m 矩阵,Sigma(通常用大写希腊字母 Sigma 表示)是一个 m x n 的对角矩阵,V^* 是一个 n x n 矩阵的共轭转置,其中 * 是上标。
与 QR 分解不同,所有矩阵都有 SVD 分解。作为求解线性回归线性方程组的基础,SVD 更稳定,是首选方法。
分解后,可以通过计算输入矩阵 X 的伪逆并乘以输出向量 y 来找到系数。
|
1 |
b = X^+ . y |
其中伪逆计算如下
|
1 |
X^+ = U . D^+ . V^T |
其中 X^+ 是 X 的伪逆,+ 是上标,D^+ 是对角矩阵 Sigma 的伪逆,V^T 是 V^* 的转置。
对于非方阵,矩阵求逆是未定义的。[...] 当 A 的列数多于行数时,使用伪逆求解线性方程会得到多个可能解中的一个。
— 第 46 页,《深度学习》,2016。
我们可以从 SVD 操作中获得 U 和 V。D^+ 可以通过从 Sigma 创建对角矩阵并计算 Sigma 中每个非零元素的倒数来计算。
|
1 2 3 4 5 6 7 |
s11, 0, 0 Sigma = ( 0, s22, 0) 0, 0, s33 1/s11, 0, 0 D = ( 0, 1/s22, 0) 0, 0, 1/s33 |
我们可以手动计算 SVD,然后计算伪逆。相反,NumPy 提供了 pinv() 函数,我们可以直接使用。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
# 通过伪逆的 SVD 进行最小二乘法 from numpy import array from numpy.linalg import pinv from matplotlib import pyplot data = array([ [0.05, 0.12], [0.18, 0.22], [0.31, 0.35], [0.42, 0.38], [0.5, 0.49], ]) X, y = data[:,0], data[:,1] X = X.reshape((len(X), 1)) # 计算系数 b = pinv(X).dot(y) print(b) # 使用系数进行预测 yhat = X.dot(b) # 绘制数据和预测 pyplot.scatter(X, y) pyplot.plot(X, yhat, color='red') pyplot.show() |
运行此示例将打印系数,并绘制带有红色拟合线的数据。
|
1 |
[ 1.00233226] |
实际上,NumPy 提供了一个函数来替换这两个步骤,即 lstsq() 函数,您可以直接使用它。
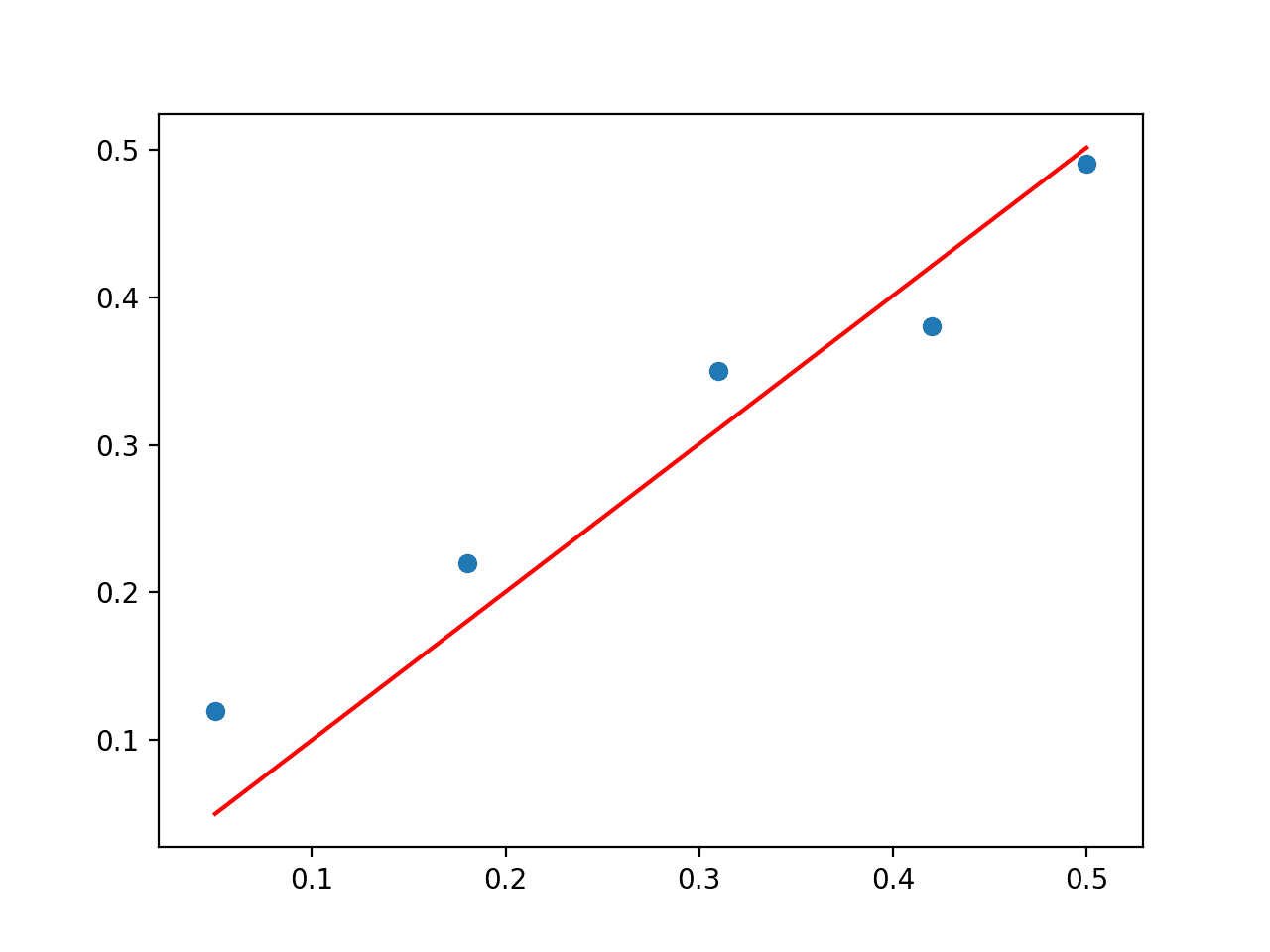
线性回归问题 SVD 解的散点图
扩展
本节列出了一些您可能希望探索的扩展本教程的想法。
- 使用内置的 lstsq() NumPy 函数实现线性回归
- 在您自己的小型人造数据集上测试每种线性回归方法。
- 加载表格数据集并测试每种线性回归方法,并比较结果。
如果您探索了这些扩展中的任何一个,我很想知道。
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
书籍
- 第 7.7 节 最小二乘近似解。《《线性代数不废话指南》》,2017。
- 第 4.3 节 最小二乘近似。《《线性代数导论》》,第五版,2016。
- 第 11 讲 最小二乘问题。《《数值线性代数》》,1997。
- 第 5 章 正交化与最小二乘。《《矩阵计算》》,2012。
- 第 12 章 奇异值与 Jordan 分解。《《统计学线性代数与矩阵分析》》,2014。
- 第 2.9 节 Moore-Penrose 伪逆。《《深度学习》》,2016。
- 第 15.4 节 一般线性最小二乘。《《数值方法:科学计算艺术》》,第三版,2007。
API
- numpy.linalg.inv() API
- numpy.linalg.qr() API
- numpy.linalg.svd() API
- numpy.diag() API
- numpy.linalg.pinv() API
- numpy.linalg.lstsq() API
文章
教程
总结
在本教程中,您了解了线性回归的矩阵形式以及如何使用直接法和矩阵分解法来求解。
具体来说,你学到了:
- 线性回归与法方程的矩阵重构。
- 如何使用 QR 矩阵分解求解线性回归。
- 如何使用 SVD 和伪逆求解线性回归。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。







在您的介绍中,您提到了单变量问题 y=b0+b1*x,或矩阵表示法中的 Y=X.b。很明显 b 是一个 2x1 矩阵,所以 X 必须是一个 nx2 矩阵。
然而,在您实现各种求解方法时,您隐含地假设 b0 = 0,然后 X 是一个 nx1 矩阵,b 是一个 1x1 矩阵。
对于您选择的示例数据集,这会导致 b1=1.00233 的可接受解,平方偏差和为 0.00979,拟合线看起来大致 OK。但它绝对不是该数据集的最小二乘解。
如果您也拟合 b0,您将得到斜率 b1=0.78715 和 b0=0.08215,平方偏差和为 0.00186。为此,X 矩阵必须用一列 1 来增强。
如果数据集是
data = array([
[5.05, 0.12],
[5.18, 0.22],
[5.31, 0.35],
[5.42, 0.38],
[5.5, 0.49],
])
那么拟合 b0 和 b1 将如前所述得到 b1=0.78715,但使用您的形式主义,b1 变为 0.05963,对于 2 参数拟合,平方偏差和如前所述为 0.00186,但在您的情况下为 0.07130。
您的演示通常非常清晰,但我认为它仍然具有误导性,暗示它会产生最小二乘解。
谢谢John。
嗨,Jason,
非常感谢您这篇很棒且非常有帮助的文章!!!
我想知道这个方法如何用于二次曲线拟合,比如抛物线?
您可以使用带有指数化输入的线性模型,例如 x^2、x^3 等。例如,多项式回归。
您太棒了。我需要更多。我想告诉您您在这个领域非常出色。期待您的更多作品。谢谢。
谢谢!
嗨,Jason,
我有两个问题
系数 b 是否总是单个值?我认为它应该是一个包含每个 Xi 系数的向量。
另外,这个例子可以应用于拟合两条平行线吗?
如果您有一个输入向量,那么它就是一个系数向量。
例如 yhat = X . b
嗨,Jason,
非常感谢您迄今为止构建的整个机器学习百科全书,它确实很有帮助:)
我有一个问题:当使用 sklearn 的 Linear Regression 在您生成的相同数据集上运行时,reg.coef_ 输出的是 “0.78715288”,而不是此算法为 b 输出的 “1.00233226”。
我已经像您在这里一样传递了 X 和 y,而且我非常确定它们也使用了伪逆。您对此有什么看法?
它们执行计算方式的细微差别可能会导致系数/结果略有不同。
sklearn 库的开发是为了在许多情况下都具有鲁棒性,我预计它们在这些方面对基本方法进行了一些有用的更改。
你好 Arthur,
这不是细微差别,也与 scikit-learn 的鲁棒性无关。
区别在于 scikit-learn 的线性回归模型包含截距,而 Jason 这里没有。如果您想省略此项但仍获得与 scikit-learn 相同的 b 结果(0.78715288),则需要在求解线性回归模型之前从 X 和 y 中减去均值。
祝好,
是的,截距只是将数据进行中心化,可以这么说。就像数据预处理一样。
嗨,Jason,
很棒的教程。我正在解决一个问题,其中我的线性回归可以是垂直的(例如 x = 3)。对于这个问题,y = X . b 不起作用。您是否有任何关于如何解决垂直线问题的想法?
您是指数据列吗?
通常一列代表许多观测/样本。
也许旋转您的数据,使一列成为一行并可以输入到方法中?
我想知道是否可以从深度学习算法(如卷积神经网络(CNN)或自动编码器)的权重中提取系数?
您可以直接从神经网络中检索并保存模型权重。
你说得对。但我还有另一个问题。
目标是根据 x1 到 x3 对模型进行选择,并恢复 beta1 到 beta3 的真实值作为它们的系数。V 和 U 是未观察到的
NumberOfObservations = 10000
beta1 = 4 # 模型的真实参数值(随机选择)
beta2 = -2
beta3 = 2
# 数据生成
data = {‘ID’: pd.Series(range(1, (NumberOfObservations+1)))}
df = pd.DataFrame(data)
df[‘x1’] = np.random.normal(loc = 0, scale = 1, size = NumberOfObservations)
df[‘x2’] = np.random.normal(loc = 0, scale = 1, size = NumberOfObservations)
df[‘x3’] = np.random.normal(loc = 0, scale = 1, size = NumberOfObservations)
df[‘V1’] = beta1 * df[‘x1’] + beta2 * df[‘x2’] + beta3 * df[‘x3’]
df.loc[df[‘V1’] >=0, ‘choice’] = 1
df.loc[df[‘V1’] <0, 'choice'] = 0
对于分类问题,每一层都有几个权重,在最后一层(如果我们有 2 个类别 0 或 1)每个 Xi 都有两个权重,在这种情况下我应该如何计算系数(beta)?
我相信您描述的是二元目标,在这种情况下,您必须使用不同的解决方案,例如逻辑回归,而不是线性回归。
使用 QR 分解求解形式为 Mx = b 的线性方程组,其中 x 是未知
向量 x,在 QR 分解中如何用 Python 进行分解?
请看这个例子
https://machinelearning.org.cn/introduction-to-matrix-decompositions-for-machine-learning/
不,这没有回答我的问题。我的问题是:
Ax=b 求 x 的 QR 分解
我相信我已链接到应有所帮助的资源。
我没有能力为您准备代码示例,抱歉。
也许我不是最适合帮助您完成项目的人。
请给我一些关于这个的例子
对矩阵 M 进行对角化,使其可以写成 D = P^-1
MP,
其中 D 是对角矩阵。
本教程展示了如何计算对角矩阵
https://machinelearning.org.cn/introduction-to-types-of-matrices-in-linear-algebra/
从那里,您将获得实现您所描述的内容的足够信息。
您好,亲爱的
在线性代数中
np.linalg.pr 是什么?
用线性代数描述
请帮忙
也许您可以直接查看 API 文档
https://numpy.com.cn/doc/stable/reference/routines.linalg.html
使用 numpy,对于具有一个预测变量和一个响应变量的线性回归的通用情况。使用 matplotlib 绘制散点图和拟合线。还绘制“残差 vs 拟合”图并计算 R^2 值。使用 Anscombe 的四重奏之一作为数据集,将其结果与 R 函数 lm() 进行比较。您可能会发现 numpy.hstack()、np.ones() 和 numpy.reshape() 有用。
谁能理解这样的问题?
请我需要反馈。谢谢。
adestop0072004@yahoo.ca
您的问题是什么?